Уроки з геометрії за темою " Аксіоми стереометрії"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

 

 

 

 

Харівська вечірня (змінна) школа №3

Харківської міської ради

Харківської області

 

Методичні та дидактичні матеріали

для самостійної роботи учнів за темою:

«Перпендикулярність

 площин у просторі»

 

 

 

 

 

Розробив:

вчитель математики

ХВ(з)Ш№3

Каліта Е.Є.

 

 

 

 

Тема « Перпендикулярність  площин у просторі»

Умовно дану тему можна поділити на три частини: первинне засвоєння поняття про перпендикулярні площини; закріплення властивостей перпендикулярних  площин у просторі та перевірка знань  про перпендикулярні площини; закріплення знань і вмінь про перпендикулярні  площини.

План вивчення теми.

№ уроку	Кількість годин	Тема уроку	Тип уроку
1	1	Перпендикулярність  площин. Ознака перпендикулярності  площин.	Засвоєння нових знань і вмінь
2	1	Властивості перпендикулярних  площин.Розв’язування задач	Закріплення нових знань і вмінь
3	1	Узагальнення та систематизація вмінь учнів. Самостійна робота.	Контроль і корекція знань, умінь та навичок.

 

  Урок 1.

Тема уроку : «Перпендикулярність  площин.

      Ознака перпендикулярності  площин.»

Мета уроку:

Навчальна : Ознайомити учнів з поняттями та ознакою перпендикулярності  площини; виробити вміння застосовувати  знання до розв’язування задач.

Розвивальна : розвивати абстрактне уявлення про світ.

Виховна : виховувати охайне ставлення до роботи.

Тип уроку: урок засвоєння нового матеріалу.

Форма організації навчальної діяльності: групова.

Методи і прийоми навчання:

Дидактичне та матеріально-технічне забезпечення:

Хід уроку.

1. Організаційна частина (  3 хв.): привітання, перевірка відсутніх на уроці.
2. Підготовка учнів до вивчення нового матеріалу (  5 хв.):

1. Довести до відома учнів теми програми, теми і мети уроку, плану уроку.
2. Контроль знань учнів по попередньому матеріалу ( актуалізація знань).

3. Вивчення нового матеріалу, поточне повторення, первинне закріплення ( 29 хв.): викладання нового матеріалу (мотивація навчання).

Закріплення вивченого матеріалу.

4. Підведення підсумків уроку ( 5 хв.): аналіз відповідей, оцінювання відповідей
5. Видача домашнього завдання ( 3 хв.)

 

 

Урок 2.

Тема уроку : «Властивості перпендикулярних  площин.    Розв’язування задач.»

Мета уроку:

Навчальна : Ознайомити учнів з властивостями перпендикулярних площин; виробити вміння застосовувати  знання до розв’язування задач.

Розвивальна : розвивати абстрактне уявлення про світ.

Виховна : виховувати дисциплінованість.

Тип уроку: урок закріплення нових знань і вмінь

Форма організації навчальної діяльності: робота в малих (рівносильних) групах

Методи і прийоми навчання:

Дидактичне та матеріально-технічне забезпечення:

Хід уроку.

6. Організаційна частина (  3 хв.): привітання, перевірка відсутніх на уроці.
7. Підготовка учнів до вивчення нового матеріалу (  5 хв.):

3. Довести до відома учнів теми програми, теми і мети уроку, плану уроку.
4. Контроль знань учнів по попередньому матеріалу ( актуалізація знань).

8. Вивчення нового матеріалу, поточне повторення, первинне закріплення ( 29 хв.): викладання нового матеріалу (мотивація навчання).

Закріплення вивченого матеріалу.

9. Підведення підсумків уроку ( 5 хв.): аналіз відповідей, оцінювання відповідей
10.  Видача домашнього завдання ( 3 хв.)

 

Урок 3.

Тема уроку : «Узагальнення та систематизація вмінь учнів.

      Самостійна робота.»

Мета уроку:

Навчальна : Узагальнити  та систематизувати вміння учнів; виробити вміння  самостійно застосовувати  знання до розв’язування задач.

Розвивальна : розвивати вміння аналізувати та синтезувати знання.

Виховна : виховувати культуру поведінки у колективі.

Тип уроку: урок контролю і корекції  знань, умінь та навичок.

Форма організації навчальної діяльності: індивідуальна.

Методи і прийоми навчання:

Дидактичне та матеріально-технічне забезпечення:

Хід уроку.

11. Організаційна частина (  3 хв.): привітання, перевірка відсутніх на уроці.
12. Підготовка учнів до вивчення нового матеріалу (  5 хв.):

5. Довести до відома учнів теми програми, теми і мети уроку, плану уроку.
6. Контроль знань учнів по попередньому матеріалу ( актуалізація знань).

13. Вивчення нового матеріалу, поточне повторення, первинне закріплення ( 29 хв.): викладання нового матеріалу (мотивація навчання).

Закріплення вивченого матеріалу.

14. Підведення підсумків уроку ( 5 хв.): аналіз відповідей, оцінювання відповідей
15. Видача домашнього завдання ( 3 хв.)

 

 

 

 

 

 

Вправи на розвинення просторових уявлень

1.На малюнку зображено одну й ту саму фігуру, але в різних положеннях. Де повинна стояти «зірочка» у кожній із фігур?

 

2. Куб із ребром 5 см пофарбували в зелений колір. Потім його розрізали на маленькі кубики, ребро кожного з них дорівнює 1 см. Скільки кубиків мають:

а) 1 зафарбовану грань;  в) 3 зафарбовані грані;

б) 2 зафарбовані грані;  г) жодної зафарбованої грані?

3. Які з кубиків відрізняються від першого тільки розміщенням у просторі?

1	2	3	4	5

4. На гранях куба написані букви A,B,C,D,E,F. Визначте, які букви написані на протилежних гранях куба за його рисунками в трьох положеннях у просторі.

5.(жарт) Що зображено на рисунках?

А)

Б)

Тестові завдання

Варіант 1.

1.Яка з наведених фігур не є основною фігурою стереометрії?

а) пряма;  б) куля;  в) точка;  г) площина.

2. Яке з наведених тверджень є неправильним?

а) Пряма і площина називаються паралельними, якщо вони не мають спільних точок.

б) Пряма і площина називаються перпендикулярними, якщо вони перетинаються.

в) Кут між мимобіжними прямими є кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим .

г) Через кожну точку прямої можна провести на площині перпендикулярну до неї пряму і до того ж тільки одну.

3. Яке з наведених тверджень є теоремою шкільного курсу геометрії?

а) Пряма перпендикулярна до однієї з двох паралельних прямих перпендикулярна і до другої прямої.

б) Через будь-які дві точки можна провести пряму і тільки одну.

в) Пряма перпендикулярна до площини перетинає цю площину і перпендикулярна до будь якої прямої цієї площини.

г) Через точку поза площиною можна провести одну пряму перпендикулярну до даної площини.

4. Яке з наведених тверджень правильне?

а) Через три точки завжди можна провести пряму і тільки одну.

б) Через три точки в жодному разі не можна провести прямої.

в) Через одну точку можна провести 1 000 000 прямих.

г) На площині не існує інших точок, крім тих, що належать певній прямій.

Варіант 2.

1.Яка з наведених фігур не є основною фігурою стереометрії?

а) площина; б) куб; в) пряма;     г) точка.

2. Яке з наведених тверджень є неправильним?

а) Пряма і площина називаються перпендикулярними, якщо вони перетинаються.

б) Пряма і площина називаються паралельними, якщо вони не мають спільних точок.

в) Кут між мимобіжними прямими є кут між прямими, які перетинаються і паралельні відповідно даним мимобіжним прямим .

г) Через кожну точку прямої можна провести на площині перпендикулярну до неї пряму і до того ж тільки одну.

3. Яке з наведених тверджень є теоремою шкільного курсу геометрії?

а) Через будь-які дві точки можна провести пряму і тільки одну.

б) Пряма перпендикулярна до однієї з двох паралельних прямих перпендикулярна і до другої прямої.

в) Пряма перпендикулярна до площини перетинає цю площину і перпендикулярна до будь якої прямої цієї площини.

г) Через точку, що не лежить на прямій, можна провести на площині не більше однієї прямої, паралельної поданій.

4. Яке з наведених тверджень правильне?

а) Через будь-які дві точки можна провести пряму і до того ж не одну.

б) Яка б не була пряма, існує 1 000 000 точок, що не належать їй.

в) Із трьох точок на певній прямій жодна не лежить між двома іншими.

г) Довжина відрізка не може дорівнювати 10 ^-2 см.

Картка контролю теоретичних знань

1.Стереометрія – це розділ ………………………………, у якому вивчаються фігури у ……………………………….. «Стереос» -  …………………, «метрео» - ……………………. Основними фігурами у просторі є ……………………………………………. …………………………………………………………………………………… Властивості фігур (теореми) в геометрії встановлюються шляхом ………………………………………….., тобто логічного ……………………, яке опирається на аксіоми і …………………………………. , які вже було доведено.   2.Група тверджень про існування перпендикулярних прямих і площин  (заповніть пропуски у та проілюструйте їх зміст малюнками): № Малюнки Формулювання 1   Щоб через точку у просторі  провести три  взаємно перпендикулярні прямі треба…………………………….. …………………………………… 2   Щоб знайти множину точок простору рівновіддалених від  трьох даних точок, які не лежать на одній прямій треба …………………………..…... ……………………………………… 3   Яке взаємне розташування прямої та площини , перпендикулярних до однієї даної прямої?……………….. ………………………………………

 

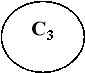
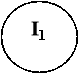
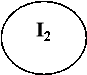
Опорний конспект

 

Схема доведення теореми Т.1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант.

 

Дайте відповідь на запитання.

1.Які із зазначених точок належать площині α?

Відповідь: ……………………………

2.Які із зазначених точок не належать площині α?

Відповідь: ……………………………

3. Які із зазначених точок належать площині β?

Відповідь: ……………………………

4.Які із зазначених точок не належать площині β?

Відповідь: …………………………..

5. Які із зазначених точок належать  одночасно площинам α і β?

Відповідь: ……………………………………………….

6.Які із зазначених точок не належать ні одній із зазначених площин?

Відповідь: ……………………………………………….

7.Чи перетинаються  площини α і β?  Обгрунтувати .

Відповідь: ……………………………………………….

8.Яка із зображених прямих є лінією перетину площин α і β, якщо вони перетинаються?

Відповідь: ……………………………………………….

9. Знайти спільні точки прямій АС та площини β.

Відповідь: ……………………………………………….

10.Знайти на малюнку прямі:

а) які належать площині α. Відповідь…………………

б) які належать площині β. Відповідь…………………

в) які не належать ані площині α, ані площині β.

Відповідь: ……………………………………………….

11.Заповніть таблицю та відповідьте на запитання.

Запитання	Варіант	Пара прямих
	1	АК і АD	AD і BE	MB і AC	AK і MD	BE і AC	AD і AC
	2	AD і MD	MD і BE	AK і MB	MD і MB	AC і MD	AK і AC
	3	AD і AC	AK і MD	MB і AC	MB і BE	AD і MB	MD і AC
	4	MD і BE	AD і BE	AK і AD	BE і AC	MD і MB	AK і MB
	5	AD і BM	AK і AC	MD і AC	AD і MD	AK і MC	МВ і ВЕ
Визначає дана пара прямих площину?
Зображена ця площина на малюнку?
Як позначена ця площина?
На основі якої аксіоми зроблено висновок?

 

 

 

 

 

 

 

 

 

 

 

Опорний конспект

 

Схема доведення теореми Т.2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблиця взаємного розміщення прямої і площини

Завдання. Опишіть та проілюструйте всі можливі випадки розміщення прямої і площини у просторі.

Малюнок	Взаємне розміщення прямої і площини	Наявність спільних точок
	Пряма і площина не перетинаються	Спільних точок не мають
	Пряма перетинає площину	Одна (єдина) спільна точка
	Пряма лежить у площині	Безліч спільних точок

 

 

 

 

 

 

 

 

 

 

Сутність способу доведення від супротивного

1. Робиться припущення (допущення), протилежне тому, що треба довести. 2. З’ясовується, що випливає зі зробленого припущення на основі відомих      теорем, аксіом, умови задачі або теореми. 3. Установлюється протиріччя між тим, що одержано, і тим, що відомо з   умови задачі або теореми, аксіом, або теорем, які доведено раніше. 4. Робиться висновок: наше припущення неправильне, а правильне те, що   треба було довести.

Картка контролю

Доведення від супротивного
Задача № 773	Задача № 774
Дано: Точки А, В, С,D не лежать в одній площині. Чи можуть прямі ABі CD перетинатися? А пряміACі BD?	Дано: Прямі KL іMN не лежать в одній площині. Чи можуть пряміKMі LN перетинатися? А пряміLM іKN?
Доведення	Доведення
1.Припустимо, що прямі ABі CD перетинаються. Тоді через них можна провести площину α (За Теоремою 2), а отже, точки А, В, С,D лежать в площині α, що суперечить умові задачі. Тоді прямі ABі CD не перетинаються.	1….....
2.Аналогічно, припустимо, що прямі ACі BD перетинаються. Тоді через них можна провести площину β (Теорема 2), а звідси випливає, що Аβ, Сβ, Dβ і Вβ, що суперечить умові задачі. Тоді прямі ACі BD не перетинаються.	2……..
Відповідь: ABі CD не перетинаються; ACі BD не перетинаються.	Відповідь:

 

 

 

 

Математичний диктант

Варіант 1.

1. На якому з наведених малюнків правильно зображено куб і дві прямі, що перетинаються?

 

А	Б	В

Г	Д

 

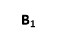
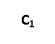2. На малюнку зображено куб ABCDA₁B₁C₁D₁  і три точки, що є серединами сторін AB, ADіCC₁. Скільки ребер куба перетинає площина, яка проходить через ці точки?

 

A	Б	В	Г	Д
Три	Чотири	П’ять	Шість	Сім

 

 

 

 

 

 

Математичний диктант

Варіант 2.

1. На якому з наведених малюнків правильно зображено куб і дві прямі, що перетинаються?

 

А	Б	В

Г	Д

 

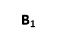2. На малюнку зображено куб ABCDA₁B₁C₁D₁  і три точки, що є серединами сторін AD, DCіB₁C₁. Скільки ребер куба перетинає площина, яка проходить через ці точки?

 

A	Б	В	Г	Д
Три	Чотири	П’ять	Шість	Сім

 

 

 

 

Опорний конспект

 

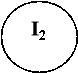
Схема доведення теореми Т.3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контроль теоретичних знань та практичних навичок.

Завдання. Відповідьте на запитання та виконайте малюнок.

1.В просторі задано три точки А, В, С. Скільки існує площин, які проходять через ці точки?

Відповідь: ……………………………………

2.Зобразіть площину α, якій належать точки А, В, С.

3.Проведіть прямі АВ, ВС і АС.

4.Чи належать прямі АВ, ВС, АС площині α?

Відповідь: ………………………………………………………………………..

5.Зафіксуйте на малюнку точку D яка не належить площині α

6.Скільки площин можна провести через точку D та кожну пряму АВ, ВС і АС? Відповідь: ………………………………………………………………………..

7.Провести прямі  DA, DB, DC.

8.Яким площинам належить точка D?

Відповідь: ………………………………………………………………………..

9.Чи перетинаються ці площини? Якщо перетинаються, то по яким лініям?

Відповідь: ………………………………………………………………………..

10.Через точку А провести пряму а, котра не належить площині α та не збігається з AD.

11.Як розташовані пряма а та площина α? Скільки площин можна провести через а та AD?

Відповідь: ………………………………………………………………………..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Конкурс малюнків (креслень)

Завдання.

Задано три площини α, β, γ. Вони попарно перетинаються. Зобразіть випадки, коли площини α, β, γ:

а) не мають спільну точку;

б) мають одну спільну точку;

в) мають спільну пряму (безліч спільних точок)

Вказівка: Біля кожного креслення вкажіть пп.а, б або в.

 

 

 

 

 

 

 

 

 

Робота в парах

Варіант 1.

Дано чотирикутник ABCD який лежить в одній площині. Точка D цього чотирикутника лежить в площині α. Пряма AB перетинає площину в точці K, пряма BC– в точці M. Чи існує  похибка у малюнку? Як виправити похибку, якщо вона зроблена в знаходженні: а) точкиK; б) точкиM?

Відповідь:………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………….

 

Варіант 2.

На малюнку дано три прямі які попарно перетинаються. Вони перетинають площину α. Чи існує  похибка у малюнку?

Як виправити похибку, якщо вона зроблена в знаходженні: а) точкиK;

б) точкиM, в) точкиD?

Відповідь:…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

 

Опорний конспект

Схема аксіоматичного уведення в стереометрію

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Математичний диктант

Завдання.Дано куб ABCDA₁B₁C₁D₁.

1.Площини яких граней визначають точки:

Варіанти		Точки	Грань
1	а)	A, B, D
	б)	B, B1, C
2	а)	A1,B1, B
	б)	A1 , B1, C1
3	а)	D,D1, C1
	б)	B1, C1, D1
4	а)	C, D, A
	б)	A, A1,B1
5	а)	D1, C1, C
	б)	C1,B C

 

2.Ребро куба дорівнює 8 см. Точки – середини відповідних ребер. Побудувати переріз та знайти його площу.

 

Варіант	1	2	3	4	5
Січна	MFE	NKD1	LED	FENP	MNP

 

Задачі та теореми, методи їх розв’язання і доведення

№ з/п	Тип задачі (теореми)	Метод доведення, який використовується найчастіше	Приклади задач (теорем)
I.Задачі на доведення та теореми
1	Задачі на доведення існування геометричного об’єкта («Існує …», «Можна провести …»)	Конструктивний (за допомогою опису уявлюваних побудов). Кожен крок побудов має бути обгрунтований	Теорема 1. (перша частина)
2	Задачі на доведення не існування геометричного об’єкта	Міркування від супротивного
3	Задачі на доведення єдності геометричного об’єкта (точки, прямої, площини)	Міркування від супротивного	Теорема 1. (друга частина)
4	Задачі на доведення не єдності геометричного об’єкта («Можна провести дві……..», «Можна провести більш як одну………»)	Конструктивний (за допомогою опису уявлюваних побудов).
II. Найпростіші позиційні задачі на зображенні куба, прямокутного паралелепіпеда, піраміди
1	Задачі на побудову точки перетину прямої і площини	Розв’язання здійснюється за схемою: 1.Аналіз 2.Побудова (фактичні побудови за допомогою лінійки на зображенні просторових тіл) 3.Доведення 4.Дослідження
2	Задачі на побудову прямої перетину двох площин

 

Графічний тренінг

 

ДОДАТКОВІ ВПРАВИ.

Варіант 1

1.Укажіть пряму перетину площин PSBі ASD.

A	Б	В	Г	Д
AD	SA	NB	SP	SN

 

 

 

2.Побудуйте переріз куба площиною, що проходить через три задані точки.

 

 

 

 

 

 

3.Побудуйте переріз піраміди площиною, що проходить через три задані точки.

 

 

 

 

 

 

 

Графічний тренінг

 

 

Варіант 2

1.Укажіть пряму перетину площин AMSі CSB.

A	Б	В	Г	Д
SK	SM	SC	AK	BC

 

 

 

2.Побудуйте переріз куба площиною, що проходить через три задані точки.

 

 

 

 

 

 

3.Побудуйте переріз піраміди площиною, що проходить через три задані точки.

 

 

 

 

 

 

 

Самостійна робота

Варіант 1.

Початковий і середній рівні (1 бал)

У завданнях 1-3 користуючись малюнком, на якому зображено прямокутний паралелепіпед ABCDA₁B₁C₁D₁, позначте одну правильну, на вашу думку, відповідь.

1.Укажіть точку, яка належить площині АВС

а) А₁    б) В₁    в) С₁   г) D д) D₁

2.Укажіть пряму, по якій перетинаються площини AD₁D іABC

а)AB б)BC в)CD г)AD д)AC

3. Укажіть площину, якій належать прямі BDіBC₁

а) (ABC)  б) (BCC₁)  в) (ACB₁)  г) (BDC₁)  д) (B₁BD)

4. Скільки площин можна провести через точкиM,N, іL, якщо MN= 12 см, NL= 5 см, ML= 13 см?

а) Нескінченну множину б) Тільки три

в) Тільки одну   г) Жодної

5. Дано прямуb і точкуB. Скільки різних площин можна провести через них, якщо точкаB не належить прямійb ?

а) Тільки дві   б) Жодної

в) Тільки одну   г) Нескінченну множину

6. Заповніть пропуски в реченні.

Якщо дві ……… прямої належать ………………, то вся пряма належить цій ……………………………………..

 

Достатній рівень (3 бали)

7. Прямі ACі BDне лежать в одній площині. Доведіть, що прямі ABі CD не лежать в одній площині.

 

Високий рівень (3 бали)

8. Доведіть, що в просторі існують чотири точки, які не лежать в одній площині.

 

 

 

Самостійна робота

Варіант 2.

Початковий і середній рівні (1 бал)

У завданнях 1-3 користуючись малюнком, на якому зображено прямокутний паралелепіпед ABCDA₁B₁C₁D₁, позначте одну правильну, на вашу думку, відповідь.

1.Укажіть точку, яка не належить площині A₁B₁C₁

а) А₁    б) В₁    в) С₁   г) D д) D₁

2.Укажіть пряму, по якій перетинаються площини ABB₁ іBCD

а)AB б)BC в)CD г)AD д)AC

3. Укажіть площину, якій належать прямі AB₁іAC

а) (ABC)  б) (BCC₁)  в) (ACB₁)  г) (BDC₁)  д) (B₁BD)

4. Скільки площин можна провести через точкиA,B, іC, якщо AC= 7 см,

BC= 3 см, AB= 4 см?

а)Тільки дві  б) Тільки три

в) Жодної   г) Нескінченну множину

5. Дано прямуb і точкуB. Скільки різних площин можна провести через них, якщо точкаB  належить прямійb ?

а) Тільки три   б) Тільки одну

в)Нескінченну множину г) Жодної

6. Заповніть пропуски в реченні.

Якщо двірізні прямі мають спільну  …………….., то через них можна провести ……………., і до того ж тільки ………………………

 

Достатній рівень (3 бали)

7. ТочкиA,Bі пряма CDне лежать в одній площині. Доведіть, що прямі ABі CDне перетинаються.

 

Високий рівень (3 бали)

8. Доведіть, що в просторі існують дві прямі, які не лежать в одній площині.

 

 

 

 

Відповіді й розв’язання до завдань самостійної роботи

Варіант 1.

1. Д   2. Г     3. Г      4. В       5. В

6. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

7. Доведення (від супротивного). Припустимо, що прямі ABі CDлежать в одній площині. Тоді точки A,B, C, Dлежать у цій самій площині. Звідси випливає, що прямі ACі BDлежать в одній площині, а це суперечить умові задачі. Отже, AB і CD не лежать в одній площині.

8. Доведення. Візьмемо дві різні точки A і B, проведемо пряму AB. Візьмемо точку C поза прямою AB і проведемо площину через пряму AB і точку C. Нарешті, візьмемо точку D поза площиною ABC. Таким чином, точки A, B, C, D не лежать в одній площині.

 

 

Варіант 2.

1. Д   2. А     3. В      4. Г      5. В 

6. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

7. Доведення (від супротивного). Припустимо, що прямі ABі CDперетинаються. Тоді вони лежать в одній площині. Таким чином, точки A, B, C, Dлежать у цій самій площині, отже, пряма CD і точки A та Bлежать в одній площині, що суперечить умові задачі. Отже, ABі CDне перетинаються.

8. Доведення. Виберемо (див. задачу 8 варіанта 1) чотири точки, які не лежать в одній площині, тоді прямі AB і CD також не лежатимуть в одній площині.