Уроку геометрії "Розв'язування задач на подібність трикутників

Розробка уроку геометрії в 8 класі на тему: «Розв’язування задач на застосування подібності трикутників»

Тема: Розв’язування задач на застосування подібності трикутників

Мета: освітня: продовжити формувати вміння і навички учнів застосовувати вивчені ознаки подібності трикутників до розв’язування задач, удосконалити навички розв’язування задач практичного змісту;

розвиваюча: розвивати логічне мислення, математичну грамотність мовлення, критично оцінювати здобуту інформацію та її джерела, виокремлювати головне, оцінювати правильність і раціональність розв’язування математичних задач, обґрунтовувати твердження, приймати рішення в умовах неповної, надлишкової, точної та ймовірнісної інформації, аналізувати, робити висновки, використовувати отриману інформацію в особистому житті.

виховна: виховувати пізнавальну активність, культуру спілкування, формування культури праці, сумлінного ставлення до матеріальних і духовних цінностей.

Тип уроку: формування вмінь та навичок.

Обладнання: підручник, комп’ютер, презентація, дошка, зошит, креслярське приладдя.  

Епіграф уроку.

«Блаженство тіла полягає в здоров'ї, а блаженство розуму – у знанні» 

Очікувані результати:

Після уроку учні зможуть:

       розв’язувати задачі на застосування подібності трикутників;

       робити логічні висновки, аналізувати вивчений матеріал;

       оцінювати правильність і раціональність розв’язування математичних задач;

       творчо мислити та самостійно працювати.

Хід уроку

1.                     Мотивація навчальної діяльності, повідомлення теми, мети уроку.

Тема Сьогоднішнього  уроку «Розв’язування задач на застосування подібності трикутників», а епіграфом до уроку  будуть слова  давньогрецького філософа досократського періоду, математика, астронома, засновника іонійської школи натурофілософії  Фалеса Мілетського «Блаженство тіла полягає в здоров'ї, а блаженство розуму – у знанні».

Послухайте притчу. Колись давно, в одному місті, жив мудрець. Слава про його мудрість рознеслась далеко навколо його рідного міста, люди здалеку приходили до нього за порадою.

Але був у місті чоловік, який заздрив його славі. Прийшов він якось на луг, спіймав метелика, посадив його між зімкнутих долонь і подумав:

 – Піду я до мудреця і спитаю у нього: скажи, о наймудріший, який метелик у мене в руках: живий або мертвий?  Якщо він скаже «мертвий», я відкрию долоні, метелик полетить.  Та, якщо він скаже «живий» – я зімкну долоні, і метелик помре. От тоді всі й зрозуміють, хто з нас розумніший.

Так все і сталось. Заздрісник прийшов у місто і спитав у мудреця:

– Скажи, о наймудріший, який метелик у мене в руках: живий чи мертвий?

Пильно дивлячись в очі, мудрець сказав:

– Все в твоїх руках!

Запитання. Чи сподобалась вам відповідь мудреця? Чи правильно він повів себе?  Чи має  вислів  мудреця «Все в твоїх руках!» відношення до нашого уроку?

          Актуалізація опорних знань

Інтерактивна технологія «Відкритий мікрофон».

       Сформулюйте ознаки подібності прямокутних трикутників.

       Чи подібні трикутники АВС і КРТ, якщо в них ∠А=50°, ∠В=60°, ∠Р=60°, ∠Т=70°?

       Гострий кут одного прямокутного трикутника дорівнює 30°, а іншого 60°. Чи подібні ці трикутники?

       Сформулюйте ознаку подібності  трикутників за трьома сторонами.

       Чи подібні рівнобедрені трикутники, якщо вони мають прямі кути?

       Як провести пряму, яка б перетинала дві сторони трикутника паралельно до третьої сторони, щоб вона відтяла від даного трикутника подібний йому з коефіцієнтом ¾? Пояснити.

       Сформулюйте ознаку подібності трикутників за двома сторонами і кутом між ними.

       У прямокутному трикутнику побудовано проекції катетів на гіпотенузу. Скільки пар подібних трикутників утворилося?

       Сформулюйте ознаку подібності трикутників за двома кутами.

       Чи подібні два рівнобедрені трикутники за основою і кутом при основі?

Отже, ми повторили ознаки подібності трикутників, а зараз пропоную застосувати ці знання до розв’язування задач практичного змісту, які вам стануть у пригоді впродовж вашого життя.

 Учні розв’язують задачі усно, із докладними міркуваннями та коментарями.  Задачі виведено на слайді в презентації з підручника                А. Мерзляк, В. Полонський, М. Якір  «Геометрія 8».

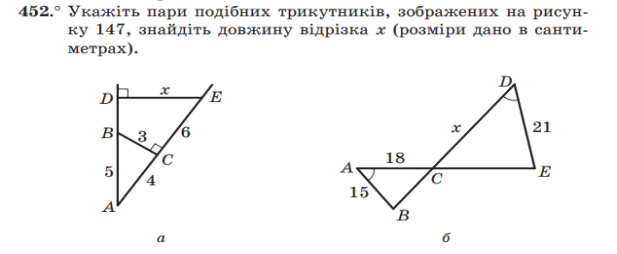
Задача № 452а

    Знайти х

Розв’язання. ∆АCВ~ ∆DЕ за двома кутами.

Відповідь: 6

Задача №452 б

   Знайти х

                                                 Розв’язання

за двома кутами. = ;   = ;  x = = 25,2.

                                                                        Відповідь: 25,2.

       Перегляд відео  Фалес Мілетський (Історія одного вченого).               Посилання на відео https://youtu.be/et_IdDRXLXY

Ще раз хочу нагадати, що саме узагальнену теорему Фалеса було покладено в основу вивчення подібності фігур, що дало змогу розв’язати багато практичних задач.

ІІІ. Формування вмінь і навичок.

Задача Фалеса: визначте відстань від берега до корабля в морі, знаючи висоту щогли 20 м, довжину великого пальця -4  см, відстань від очей до руки – 60 см.

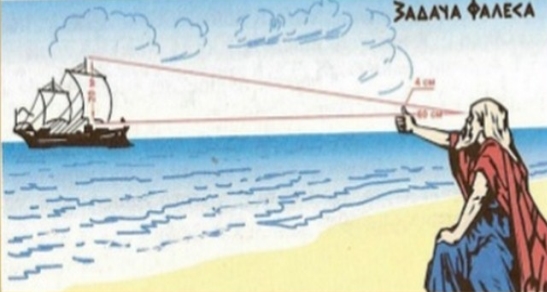
Побудуємо модель нашої задачі.

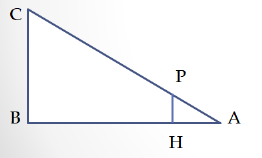
Дано:  СВ=20m  -висота щогли;

             РН=4см-довжина пальця;

             АН=60см- відстань від очей  до руки.

Знайти: АВ-? відстань  від берега до корабля в морі

  Розв’язання.

1. Застосуємо Т. Фалеса і запишемо  співвідношення в наших~∆

=

         підставимо відомі величини в см

 =    застосуємо  правило  пропорції

Х== 30000(см)=300(м)

Відповідь: відстань від берега до корабля становить 300 м.

Руханка, посилання https://youtu.be/6iJaHoVGPZI?feature=shared

432. Знайдіть висоту вежі , якщо відстані від спостерігача до жердини та до вежі відповідно дорівнюють 1,5 м і 39 м, висота жердини — 3 м, а зріст спостерігача — 1,8 м

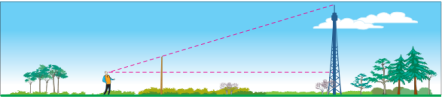
Побудуємо модель нашої задачі.

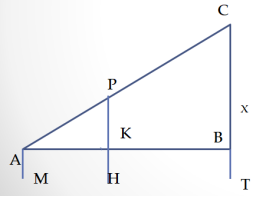
Дано:  АВ=39m  -відстань до  вежі;

             РН=3м-висота жердини;

             АН=1,5м- відстань від очей  до жердини.

             АМ=1,8м зріст людини

Знайти: СТ-?  Висота вежі

  Розв’язання.

1. Застосуємо  Лему про подібні трикутники  і запишемо співвідношення для наших трикутників.

=

 підставимо відомі величини в см

 =    застосуємо  правило  пропорції

Х==31,2(м)

СТ=СВ+ВТ=31,2 +1,8=33(м)

Відповідь:  висота вежі становить 33 м.

470. Поясніть за допомогою рисунка 149, як можна знайти ширину BM річки, використовуючи подібність трикутників.

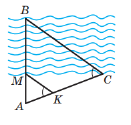
     1. МК ІІ ВС  за рівними відповідними кутами ˂К=˂С.

     2. ∆АМК ~∆АВС  за двома кутами.

за  теоремою Фалеса  ВМ=

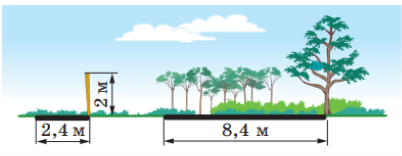
472.Знайдіть висоту дерева, якщо довжина його тіні дорівнює 8,4 м, а довжина тіні від вертикального стовпа заввишки 2 м у той самий час доби дорівнює 2,4 м.

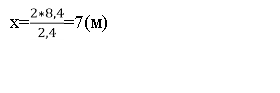
   ІУ. Діагностика знань і умінь.

Тест за підручником А. Мерзляк, В. Полонський, М. Якір  «Геометрія 8».

V. Підсумки уроку. Домашнє завдання.

Чи можемо зробити висновок: ознаки подібності трикутників дають можливість вирішити багато практичних питань?

Домашнє завдання:

1.Повторити п.12-14.

2.Розв’язати задачі №469; №471.