Узагальнююча таблиця "Чотирикутники"

ЧОТИРИКУТНИКИ

1. 
2. Сума всіх кутів чотирикутника 360
3. S = d₁d₂ sin φ
4. Чотирикутник можна вписати в коло, якщо сума його протилежних кутів 180: , 
5. Чотирикутник можна описати навколо кола, якщо суми його протилежних сторін рівні:

Паралелограм

α – кут між сторонами;

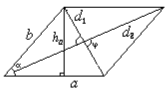
h_a – висота, проведена до сторони a,

Чотирикутник, у якого протилежні сторони попарно паралельні.

Властивості:

1. Протилежні сторони рівні (АВ=СD, ВС=АD);

2. Протилежні кути рівні (A=C, B=D)

3. Діагоналі точкою перетину діляться навпіл (АО=ОС; ВО=ОD).

4. Сума кутів, прилеглих до однієї сторони 180 (A+В=180)

5.

Ознаки:

1. Якщо в чотирикутнику протилежні сторони попарно паралельні, то це

2. Якщо в чотирикутнику протилежні сторони попарно рівні, то це  

3. Якщо в чотирикутнику дві протилежні сторони паралельні і рівні, то це

4. Якщо в чотирикутнику діагоналі точкою перетину діляться навпіл, то це

Периметр 

Площа:   S = ah_a     S = ab sin α

Прямокутник

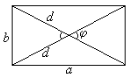
Паралелограм, у якого всі кути по 90.

1. Всі властивості паралелограма.

2. Діагоналі рівні.

S = ab

Ромб

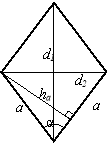
Паралелограм, у якого всі сторони рівні.

1. Всі властивості паралелограма.

2. Діагоналі перпендикулярні і є бісектрисами кутів ромба.

S = ah_a    S = a²sin α  S = d₁d₂

Квадрат

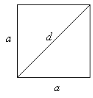
Ромб, у якого всі кути по 90 або прямокутник, у якого всі сторони рівні.

1. Всі властивості паралелограма.

2. Всі властивості прямокутника.

3. Всі властивості ромба.

S = a²  S = d²

Трапеція

BD = h – висота

Чотирикутник, у якого дві сторони паралельні, а дві інші – ні.

AD, BC – основи, АВ, СD – бічні сторони.

MN – середня лінія трапеції (сполучає середини бічних сторін)

,     МN || AD, MN || BC.

A+В=180   

Якщо , то трапеція рівнобічна. Її властивості:

1. Кути при основі рівні (A=D, B=С)

2. Діагоналі рівні (АС=ВD)

3. Відрізки діагоналей рівні (АО=ОС, ВО=ОD)