Узагальнююча таблиця "Трикутник"

ТРИКУТНИК

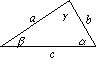
A, B, C – вершини

AB, BC, AC –   сторони

AL – бісектриса – відрізок, який ділить кут  навпіл. Ділить сторону на відрізки, пропорційні прилеглим сторонам.

BH – висота – перпендикуляр, опущений з вершини  на протилежну сторону.

CM – медіана – відрізок, який сполучає вершину  з серединою протилежної сторони. В точці перетину діляться у відношенні 2:1, рахуючи від вершини.

Середня лінія  - відрізок, який сполучає середини двох сторін . Є паралельним до третьої сторони і дорівнює її половині.

Сума кутів трикутника 180.

Ознаки рівності трикутників

І ознака – за двома сторонами і кутом між ними - якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

ІІ ознака – за стороною і двома кутами – якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники   рівні.

ІІІ ознака – за трьома сторонами – якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники рівні.

Подібні трикутники

АВС і А₁В₁С₁ називають подібними якщо їхні кути рівні, а сторони пропорційні .

АВСА₁В₁С₁: А=А₁    В=В₁    С=С_1,          – коефіцієнт подібності.  

Ознаки подібності трикутників

І ознака – за двома кутами – якщо два кута одного трикутника дорівнюють відповідно двом кутам другого трикутника, то такі трикутники подібні.

ІІ ознака – за двома сторонами і кутом між ними – якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники подібні.

ІІІ ознака – за трьома сторонами – якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні.

Теореми синусів і косинусів

 . Квадрат сторони  дорівнює сумі квадратів двох інших сторін мінус   подвоєний добуток цих сторін на косинус кута між ними.

Площа трикутника

                                     (p – півпериметр)       

Прямокутний трикутник

 c – гіпотенуза, a, b – катети.

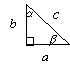
 Катет, що лежить проти кута 30, дорівнює половині гіпотенузи. 

 Медіана, проведена до гіпотенузи, дорівнює її половині.

  – відношення протилеглого катета до гіпотенузи.

  – відношення прилеглого катета до гіпотенузи.

  – відношення протилеглого катета до прилеглого.

Теорема Піфагора:

Рівнобедрений трикутник

Рівносторонній трикутник

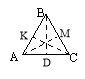
 АВ=ВС – бічні сторони

 АС – основа

 В – кут при вершині

 А=С – кути при основі

 ВD – медіана, бісектриса, висота

 АВ=ВС=АС

 А=В =С=60

 ВD, АМ, СК – медіани, бісектриси, висоти 

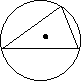
Вписане і описане кола трикутника

 Центр описаного навколо трикутника  кола лежить на перетині серединних  перпендикулярів до сторін.

 У прямокутному  – на середині  гіпотенузи.

 Центр вписаного в трикутник кола лежить  на перетині бісектрис трикутника.

 Радіус перпендикулярний до сторони.