Вчимося розв'язувати комбінаторні задачі
Любов Зваричук
ВЧИМОСЯ РОЗВ’ЯЗУВАТИ КОМБІНАТОРНІ ЗАДАЧІ
Зошит для учнів 3-4 класів
2024 рік
51(075.2)
З 42
Анотація
Зошит з друкованою основою містить додатковий матеріал до підручника «Математика» 3-4 класи (автор Богданович М. В). Виконання завдань запропонованих в зошиті, сприяє формуванню у учнів прийомів розумової діяльності (аналіз і синтез, порівняння) розвиває логічне мислення, розширює уяву молодших школярів про способи моделювання при розв’язуванні текстових задач, сприяє формуванню вміння розв’язувати задачі.
Для учнів 3-4 класів та вчителів початкової школи.
Дорогі хлопчики і дівчатка!
Цей зошит є продовженням зошита «Вчимося розв’язувати комбінаторні задачі» (1 – 2 класи). Якщо ви уже виконували завдання з цього зошита, то ви вмієте розв’язувати комбінаторні задачі способом перебору і складанням таблиць.
В 3, 4 класах ви навчитесь розв’язувати комбінаторні задачі за допомогою схеми, яку називають деревом можливих варіантів.
Успіхів вам у розв’язуванні комбінаторних задач!
Любов Зваричук
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО РОБОТИ З ЗОШИТОМ
Головна функція комбінаторних задач в початкових класах – створити умови для формування у учнів прийомів розумової діяльності (аналіз і синтез порівняння, абстрагування), для розвитку мимовільної уваги, образного мислення і для засвоєння тих понять, які входять в зміст програми.
При складанні комбінаторних задач керувались:
- логікою побудови початкового курсу математики.
- Результатами психологічних і методичних досліджень, пов’язаних з розв’язанням комбінаторних задач молодшими школярами;
- Різними видами комбінацій, які зв’язані з розміщенням, перестановками, поєднаннями.
В 1-2 класах учні розв’язували комбінаторні задачі способом перебору і за допомогою таблиць. В 3-4 класах вони знайомляться з деревом можливих варіантів.
Всі способи, за допомогою яких діти будуть розв’язувати комбінаторні задачі, не вимагають введення в програму курсу математики 3-4 класів нових понять, тобто не перевантажують учнів додатковою інформацією.
1.
- Прочитай задачу.
Одна мавпочка з’їла 8 бананів, друга – 24, третя – 16, а
четверта – 9. Скільки бананів з’їли дві мавпи?
- Познач мавпочок номерами 1, 2, 3, 4 і запиши можливі варіанти вибору двох мавпочок.
і _ і_
і _ і_
і _ і_
- Дай відповідь на запитання задачі.
а) Скільки бананів з’їли перша і друга мавпи?
![]()
б) Скільки бананів з’їли перша і третя мавпи?
![]()
в) Скільки бананів з’їли перша і четверта мавпи?
![]()
г) Скільки бананів з’їли друга і третя мавпи?
![]()
д) Скільки бананів з’їли друга і четверта мавпи?
![]()
е) Скільки бананів з’їли третя і четверта мавпи?
![]()
2.
- Прочитай задачу.
Скільки можна позначити відрізків, використовуючи
латинські букви А, В, С, Д так, щоб серед них не було відрізків, позначених однаковими буквами?
|
мал. 1
|
мал. 2
|
мал. 3
|
|
мал. 4
|
мал. 5
|
мал. 6
|
- Познач відрізки буквами на кожному малюнку і запиши, скільки вийде відрізків, які відповідають умові.
-
 Перевір свою відповідь, заповнюючи таблицю. Зафарбуй жовтим кольором ті клітинки, ких записані відповіді на запитання задачі.
Перевір свою відповідь, заповнюючи таблицю. Зафарбуй жовтим кольором ті клітинки, ких записані відповіді на запитання задачі.
|
|
А |
В |
С |
D |
||
|
A |
|
|
|
|
||
|
B |
|
|
|
|
||
|
C |
|
|
|
|
||
|
D |
|
|
|
|
|
|
![]() Скільки клітинок виявилось зафарбованими?
Скільки клітинок виявилось зафарбованими?
3.
- Прочитай задачу.
У Тамари є казки Ш.Перо, Г.К.Андерсена (А), братів Грім (Г)
і К.Єршова (Є). Дівчинка взяла на урок позакласного читання книги двох різних авторів. Книги яких авторів Тамара могла взяти на урок?
- Користуючись умовними позначеннями, покажи, як Аня могла вибрати дві книги.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Скільки варіантів вибору двох книг у тебе вийшло?
Скільки варіантів вибору двох книг у тебе вийшло?
2. Перевір свою відповідь і заповни таблицю.
|
|
П |
А |
Г |
Є |
|
П |
|
|
|
|
|
А |
|
|
|
|
|
Г |
|
|
|
|
|
Є |
|
|
|
|
![]() Зафарбуй жовтим кольором клітинки, в яких записані відповіді на запитання задачі.
Зафарбуй жовтим кольором клітинки, в яких записані відповіді на запитання задачі.
Скільки варіантів вибору двох книг у тебе вийшло?
4.
1. Прочитай задачу.
В шкільному конкурсі читців приймали участь Марина (М), Рая (Р), Віра (В), Сергій (С), Надя (Н) і Павло (П). Двоє з цих дітей було нагороджено грамотами. Хто з дітей міг отримати грамоти?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. Запиши можливі варіанти нагородження учасників конкурсу, користуючись способом перебору.
![]()
![]()
![]()
![]()
![]()
![]() Скільки варіантів у тебе вийшло?
Скільки варіантів у тебе вийшло?
![]() 3. Заповни таблицю і зафарбуй клітини, в яких записані відповіді на запитання задачі.
3. Заповни таблицю і зафарбуй клітини, в яких записані відповіді на запитання задачі.
|
|
Марина |
Рая |
Віра |
Сергій |
Надя |
Петя |
|
|
Марина |
ММ |
МР |
|
|
|
|
|
|
Рая |
|
|
|
|
|
|
|
|
Віра |
|
|
|
|
|
|
|
|
Сергій |
|
|
|
|
|
|
|
|
Надія |
|
|
|
|
|
|
|
|
Петя |
|
|
|
|
|
|
|
|
Скільки варіантів у тебе вийшло? |
|
|
|||||
5.
1. Прочитай задачу.
Як можна посадити на лавочку Настю (Н), Таню (Т), Мирона (М) і Сергія (С), щоб хлопчики (Х) і дівчатка (Д) чергувались?
 4. Користуючись умовними позначеннями, запиши всі можливі варіанти розміщення дітей на лавочці.
4. Користуючись умовними позначеннями, запиши всі можливі варіанти розміщення дітей на лавочці.
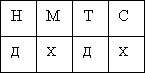
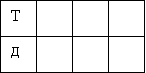
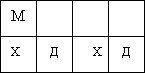
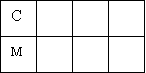
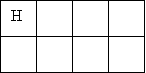
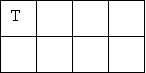
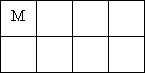
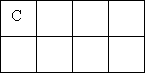
Схема 1

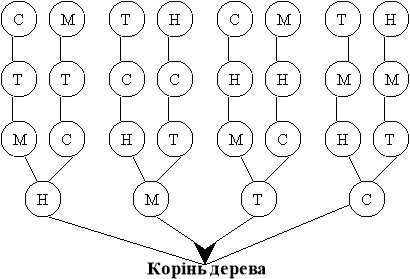 Четвертий Третій Другий Перший
Четвертий Третій Другий Перший
-
 Знайди на схемі 1 ті варіанти розміщення дітей на лавочці, які ти записав, користуючись способом перебору. Зафарбуй однакові варіанти в другому пункті і на схемі 1 одним кольором.
Знайди на схемі 1 ті варіанти розміщення дітей на лавочці, які ти записав, користуючись способом перебору. Зафарбуй однакові варіанти в другому пункті і на схемі 1 одним кольором.
 Перший
Перший
Другий
Третій Четвертий
- Заповни самостійно схему-дерево, якщо корінь дерева розміщений зверху.
- Зафарбуй червоним кольором ті гілочки, які відповідають даному розміщенню:
![]()
![]()
![]() а) б) в)
а) б) в)
-

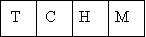 Зафарбуй синім кольором гілочки на схемі 2, які відповідають відповідному розміщенню:
Зафарбуй синім кольором гілочки на схемі 2, які відповідають відповідному розміщенню:
а) б)
6.
- Прочитай задачу.
Скільки різних двоцифрових чисел можна записати,використовуючи цифри 2,7,9, якщо цифри в цих числах можуть повторюватися?
- Виконай завдання, використовуючи різні способи:
а) перебір можливих варіантів.
|
2 |
7 |
9 |
|
2 |
7 |
9 |
|
2 |
7 |
9 |
![]() Отримали двоцифрових чисел.
Отримали двоцифрових чисел.
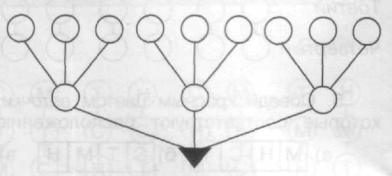 б) побудуй схему – дерево можливих варіантів. Одиниці
б) побудуй схему – дерево можливих варіантів. Одиниці
Десятки
- Використовуючи дерево можливих варіантів, запиши отримані двоцифрові числа:
![]() Отримали двоцифрових чисел.
Отримали двоцифрових чисел.
7.
- Прочитай задачу.
Коля вирішив в неділю провідати бабусю (Б), свого друга Петрика (П) і старшого брата Володю (В). В якому порядку він може організувати візити?
-
 Користуючись умовними позначеннями, запиши всі можливі варіанти? Скільки варіантів вийшло?
Користуючись умовними позначеннями, запиши всі можливі варіанти? Скільки варіантів вийшло?
![]()
![]()
![]()
![]()
![]()
![]()
-
 Перевір свою відповідь, заповни схему дерева можливих варіантів. Скільки вийшло варіантів?
Перевір свою відповідь, заповни схему дерева можливих варіантів. Скільки вийшло варіантів?
![]()
![]()
![]()
![]()
![]()
![]() 3-й візит
3-й візит
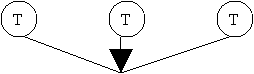 2-й візит 1-й візит
2-й візит 1-й візит
- Обведи червоним кольором гілочки, на яких показано, що Коля відвідував: а) спочатку Петрика, потім старшого брата, потім бабусю; б) спочатку старшого брата, потім бабусю, потім Петрика.
8.
- Прочитай задачу.
У клоуна чотири берети: червоний (Ч), синій (С), жовтий (Ж), зелений (З) і три сорочки:клітчаста (1), смугаста (2), в горошок (3). Чи зможе клоун на протязі двох тижнів одягати кожний день різні комплекти «берет – сорочка»?
- Користуючись умовними позначеннями, випиши різні варіанти комплекту «берет – сорочка», котрі клоун може використати для виступів.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Скільки варіантів комплектів у тебе вийшло?
Скільки варіантів комплектів у тебе вийшло?
-
 Перевір свою відповідь, заповни таблицю.
Перевір свою відповідь, заповни таблицю.
|
Берет
Сорочка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Скільки варіантів вибору комплекта «берет – сорочка» вийшло?
Скільки варіантів вибору комплекта «берет – сорочка» вийшло?
Запиши відповідь задачі.
![]()
- Заповни умовними позначеннями схеми 1 і 2.
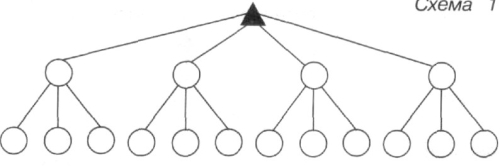
![]() Отримали варіантів.
Отримали варіантів.
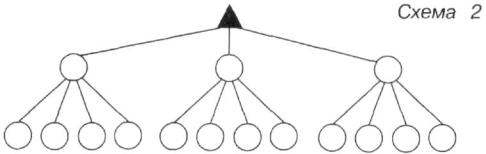
![]() Отримали варіантів.
Отримали варіантів.
- Обведи на кожній схемі гілочки дерева, які відповідають комплектам.
а) 1Ч; 2С; 3Ж – червоним кольором б) 3С; 2Ч – синім кольором;
в) 1Ж; 3Ч – зеленим кольором.
9.
- Прочитай задачу.
Скільки різних варіантів трицифрових чисел можна записати, використовуючи цифри 2, 7, 9, якщо цифри в цих числах можуть повторюватись?
- Для відповіді на запитання задачі покажи на схемі можливі варіанти запису трицифрових чисел, якщо:
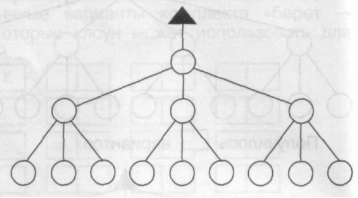 а) в розряді сотень записана цифра 2.
а) в розряді сотень записана цифра 2.
Сотні Десятки
Одиниці
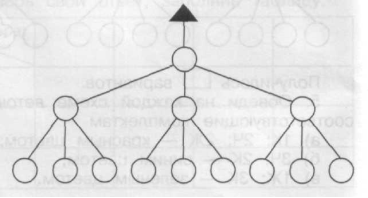 б) в розряді сотень записана цифра 7.
б) в розряді сотень записана цифра 7.
Сотні Десятки
Одиниці
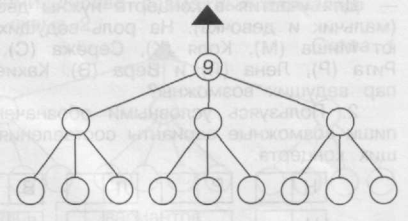 в) в розряді сотень записана цифра 9.
в) в розряді сотень записана цифра 9.
сотні десятки
одиниці
- Запиши відповідь на запитання задачі:
- Використовуючи схеми, випиши числа, в яких цифри 2, 7, 9 не повторюються
- Використовуючи ці числа, запиши різні нерівності.
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
-
 Скільки різних нерівностей можна скласти, використовуючи ці числа?
Скільки різних нерівностей можна скласти, використовуючи ці числа?
10.
- Прочитай задачу.
Для участі в концерті потрібні двоє ведучих (хлопчик та дівчинка). На роль ведучих претендують Мишко (М), Коля (К), Сергійко (С), Надійка (Н), рита (Р), Лариса ( Л) та Віра (В). Які варіанти пар ведучих можливі?
-















 Користуючись умовними позначеннями, випиши можливі варіанти пар ведучих концерту.
Користуючись умовними позначеннями, випиши можливі варіанти пар ведучих концерту.
Скільки варіантів у тебе вийшло?
-
 Заповни таблицю і зафарбуй клітинки, в яких записані відповіді на запитання задачі.
Заповни таблицю і зафарбуй клітинки, в яких записані відповіді на запитання задачі.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Скільки варіантів у тебе вийшло?
Скільки варіантів у тебе вийшло?
- Перевір свою відповідь, записавши умовними позначеннями дерево можливих варіантів – схема 1 і схема 2.
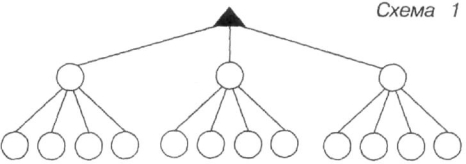
![]() Отримали варіантів.
Отримали варіантів.
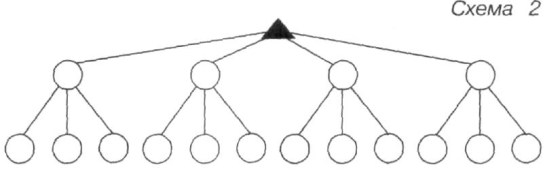
![]() Отримали варіантів.
Отримали варіантів.
-
 Скільки варіантів вибору ведучих можливі, якщо одним із них буде Віра? Зафарбуй ці пари на схемах 1 і 2 зеленим кольором.
Скільки варіантів вибору ведучих можливі, якщо одним із них буде Віра? Зафарбуй ці пари на схемах 1 і 2 зеленим кольором.
-
 Скільки варіантів вибору ведучих можливі, якщо одним із них буде Сергійко? Зафарбуй ці пари на схемах 1 і 2 синім кольором.
Скільки варіантів вибору ведучих можливі, якщо одним із них буде Сергійко? Зафарбуй ці пари на схемах 1 і 2 синім кольором.
11.
- Прочитай задачу.
Скільки різних трицифрових чисел можна записати, використовуючи цифри 4,0,2,5 якщо ці цифри в числі можуть повторюватись?
- Для відповіді на запитання задачі заповни частину схеми дерева можливих варіантів.
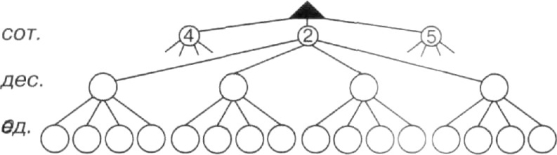
![]() Скільки чисел у тебе вийшло?
Скільки чисел у тебе вийшло?
- Здогадайся, скільки можна записати трицифрових чисел цифрами 4, 0, 2, 6 в яких:
 а) 4 сотні
а) 4 сотні
б) 5 сотень якщо ці цифри в числі можуть повторятися?
- Запиши відповідь на питання задачі.
- Запиши всі трицифрові числа, якщо в розряді десятків стоїть цифра 0.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
12.
- Прочитай задачу.
Маша займається тенісом 2 рази в тиждень. Які два дні може вибрати Маша для тренувань, якщо в понеділок і в неділю немає занять?
-
 Познач дні тижня (вівторок – В, середа – С, четвер – Ч, п’ятниця – П, субота – С) і запиши всі важливі варіанти.
Познач дні тижня (вівторок – В, середа – С, четвер – Ч, п’ятниця – П, субота – С) і запиши всі важливі варіанти.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скільки вийшло варіантів?
- Заповни таблицю і зафарбуй клітинки, в яких записані відповіді на запитання задачі?
|
|
В |
С |
Ч |
П |
СУБ |
|
В |
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Скільки клітинок вийшло зафарбованими?
Скільки клітинок вийшло зафарбованими?
13.
- Прочитай завдання.
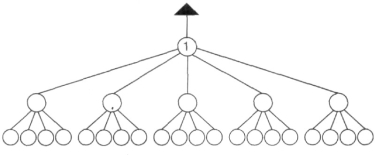
За правилами гри у волейбол із 6 членів команди (1,2,3,4,5,6), які знаходяться на ігровому майданчику, м’яч можуть відбити тільки 3 гравці. Покажи на схемі можливі варіанти ігрової ситуації, якщо м’яч прийняв гравець 1.
- Обведи червоним кольором на схемі варіанти взяття і передачі м’яча, в яких беруть участь гравці: а) 1, 5, 3; б) 1, 2, 4; в) 1, 3, 6.
- Обведи зеленим кольором на схемі ті варіанти взяття і передачі м’яча, в яких відбивав м’яч на сторону суперника гравець 5.
- Обведи синім кольором на схемі ті варіанти, в яких гравець 2 взаємодіє з гравцями 1 і 6.
- Здогадайся! Скільки варіантів ігрової ситуації можливі, якщо першим візьме м’яч:
![]() а) гравець 2?
а) гравець 2?
![]() б) гравець 3?
б) гравець 3?
![]() в) гравець 4?
в) гравець 4?
![]() г) гравець 5?
г) гравець 5?
![]() д) гравець 6?
д) гравець 6?
-
 Скільки всього може бути варіантів ігрових ситуацій?
Скільки всього може бути варіантів ігрових ситуацій?
- Покажи ламаною лінією всі можливі варіанти, якщо:
а) м’яч приймає гравець 3, а передає його на іншу сторону гравець 6.
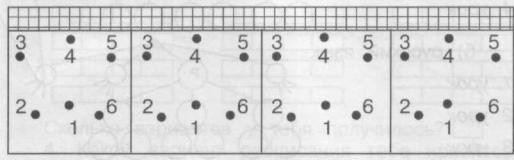
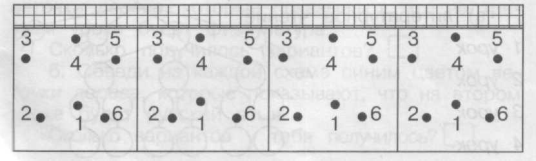
б) м’яч приймає гравець 4, а передає його на сторону суперника гравець 1.
14.
-
Прочитай задачу.
- В третьому класі в середу за розкладом 4 уроки: математика (м), українська мова (укр.), читання (Ч), фізкультура. Скільки різних варіантів розкладу уроків можна скласти на цей день?
- Використовуючи дерево можливих варіантів, покажи всі варіанти розкладу уроків в 3-му класі на середу, якщо першим уроком буде:
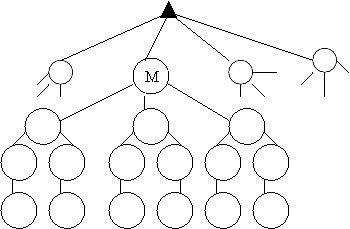 а) математика
а) математика
- урок
- урок
- урок
- урок
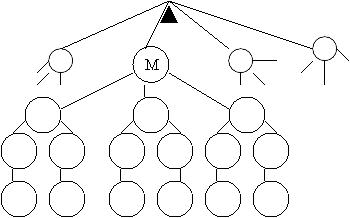 б) українська мова 1 урок
б) українська мова 1 урок
- урок
- урок
- урок
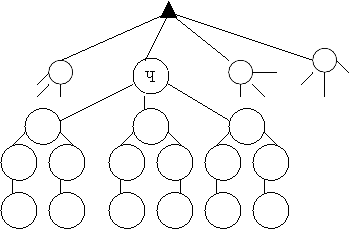 в) читання 1 урок
в) читання 1 урок
- урок
- урок
- урок
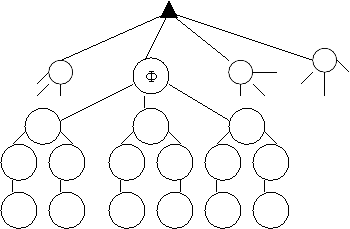 г) фізкультура
г) фізкультура
- урок
- урок
- урок
- урок
-
 Запиши всі можливі варіанти уроків на середу.
Запиши всі можливі варіанти уроків на середу.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Скільки варіантів у тебе вийшло?
-

 Який варіант розкладу тобі подобається найбільше? Познач його.
Який варіант розкладу тобі подобається найбільше? Познач його.
-
 Обведи на кожній схемі червоним кольором гілки дерева, які вказують на те, що на 3-му уроці буде фізкультура. Скільки вийшло варіантів?
Обведи на кожній схемі червоним кольором гілки дерева, які вказують на те, що на 3-му уроці буде фізкультура. Скільки вийшло варіантів?
-
 Обведи на кожній схемі синім кольором гілки дерева, які вказують, що на 2-му уроці буде українська мова. Скільки варіантів у тебе вийшло?
Обведи на кожній схемі синім кольором гілки дерева, які вказують, що на 2-му уроці буде українська мова. Скільки варіантів у тебе вийшло?
15.
- Прочитай задачу.
До класу прийшли 4 нових учні: Коля (К), Вася (В), Саша (С) і Павлик (П). Як учитель може посадити цих учнів за дві вільні парти? Скільки вибору у нього буде?
-
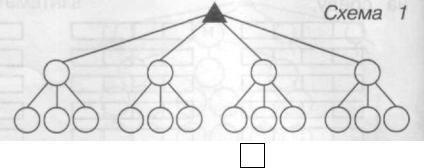 Для відповіді на запитання задачі покажи на схемі 1 всі можливі варіанти, як посадити за одну парту чотирьох учнів.
Для відповіді на запитання задачі покажи на схемі 1 всі можливі варіанти, як посадити за одну парту чотирьох учнів.
Скільки варіантів у тебе вийшло?
-
 Здогадайся! Скільки варіантів розміщення учнів можливі за іншою партою?
Здогадайся! Скільки варіантів розміщення учнів можливі за іншою партою?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Перевір свою відповідь, користуючись методом перебор
Перевір свою відповідь, користуючись методом перебор
-
 Скільки варіантів розміщення учнів можливі за двома партами?
Скільки варіантів розміщення учнів можливі за двома партами?
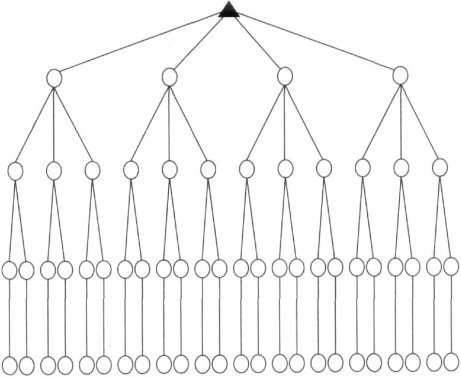
- Покажи на схемі 2 можливі варіанти розміщення 4-х учнів за двома партами (4 вільних місця).
Місце1 місце2 місце3 місце4
Схема 2
16.
- а) Накресли всі можливі відрізки, якщо точки А, В, С є їх кінцем.
А В
• •
С
•
![]() б) Скільки відрізків вийшло?
б) Скільки відрізків вийшло?
в) Запиши відрізки, які вийшли _
- а) Накресли всі можливі відрізки, якщо точки А, В, С, Д є їх кінцями.
А В
• •
Д С
• •
![]() б) Скільки відрізків отримали?
б) Скільки відрізків отримали?
в) Запиши отримані відрізки
- а) Накресли всі можливі відрізки, якщо точки А, В, С, Д, Е є їхніми початками і кінцями.
В С Д
• •
•
А Е
• •
![]() б) Скільки відрізків отримали?
б) Скільки відрізків отримали?
в) Запиши всі отримані відрізки
- Накресли всі можливі відрізки, якщо точки А, В, С, О, Е, М є їхніми початками і кінцями.
В С
• •
А Д
• •
М Е
![]() • •
• •
б) Скільки відрізків отримали.
в) Запиши отримані відрізки _
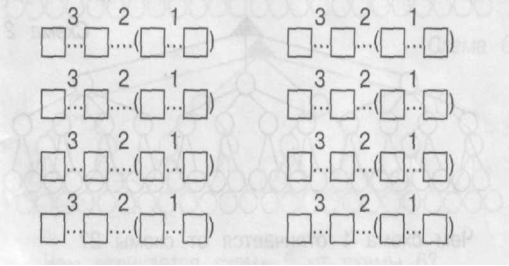
17. Постав знаки арифметичних дій, якщо вказаний їх порядок виконання.
18.
- Прочитай задачу.
З 3 класу «Б» в конкурсі взяли участь 9 учнів. Із них 3 читали вірші (В), 2 танцювали (Т), а 4 – співали (С). Грамотами нагородили одного читця, одного танцюриста і одного співака. Чи правильне твердження, що у журі було 24 варіанти вибору трьох переможців з 3»Б» класу?
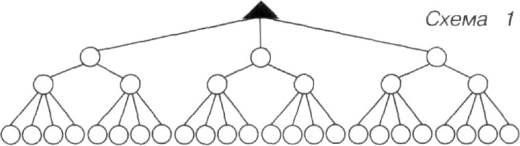
- Для відповіді на запитання задачі заповни схему 1 дерева можливих варіантів, використовуючи умовні позначення.
- Дай відповідь на запитання задачі.
- Перевір свою відповідь, заповнюючи інші схеми. Чим схема 1 відрізняється від схеми 2.
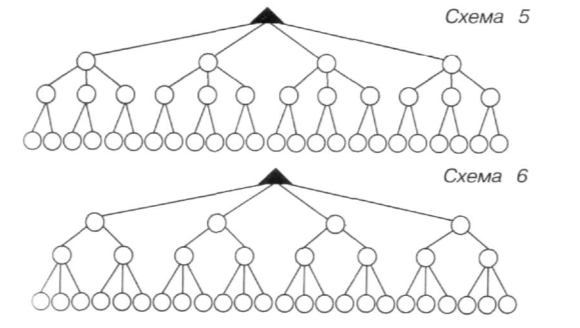 Чим схема 3 відрізняється від схеми 4? Чим схема 5 відрізняється від схеми 6?
Чим схема 3 відрізняється від схеми 4? Чим схема 5 відрізняється від схеми 6?
![]()
19.
- Прочитай завдання.
Уяви, що Міша (М), Коля (К), Віра (В) Надія (Н) і Толя (Т) повинні спуститися з гори на санках.
- Покажи на схемі 1 в якому порядку діти можуть кататися з гори, якщо Толя поїде першим, а за ним поїдуть Міша і Коля.
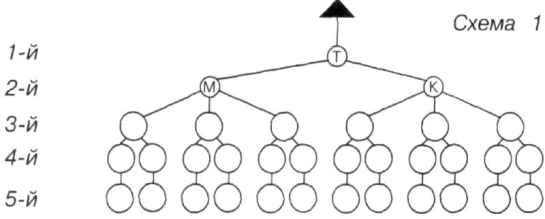
- Покажи на схемі 2 в якому порядку діти можуть спускатися з гори, якщо Толя поїде першим, а за ним поїдуть Віра і Надя.
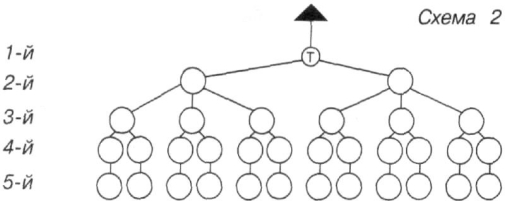
- Покажи на схемі 2 в якому порядку діти можуть
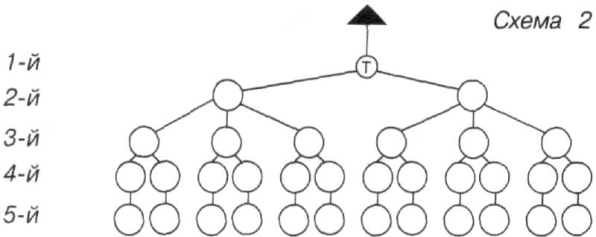
спускатися з гори, якщо Толя поїде першим, а за ним поїдуть Віра і Надя.
- Покажи на схемі 3,4,5 другі можливі варіанти катання дітей з гори.
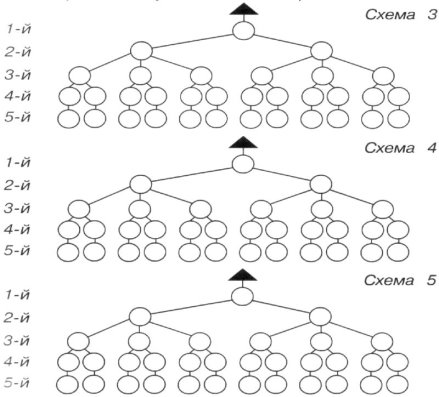
- Обведи на схемах червоним кольором гілочки дерева, які показують, що Міша спустився з гори третім.
20.
- Прочитай задачу.
Скільки різних трицифрових чисел можна записати цифрами 3,0,4,8, якщо ці цифри в числі не повторюються?
- Заповни схему дерева можливих варіантів.
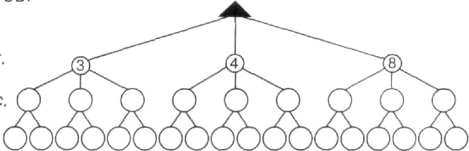 Сот. Дес. Один.
Сот. Дес. Один.
- Використовуючи схему, випиши всі числа, в яких 4 сотні
![]()
- Використовуючи схему запиши нерівності з числами, у
яких в розряді десятків записана цифра 8.
|
… … |
< |
… |
… |
< |
… |
… |
< |
|
… … |
< |
… |
… |
< |
… |
… |
< |
|
… … |
< |
… |
… |
< |
… |
… |
< |
|
… … |
< |
… |
… |
< |
… |
… |
< |
- Використовуючи схему, випиши всі числа, у яких в розряді одиниці записана цифра 0.
![]()
- Постав знаки арифметичних дій, якщо вказаний порядок
їх виконання.
![]()
![]()
![]() 3 1 2
3 1 2
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]()
![]()
![]() 3 1 2
3 1 2
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]()
![]()
![]() 3 1 2
3 1 2
… … …
3 1 2
![]()
![]()
![]()
![]()
![]() … … …
… … …
![]() Скільки різних варіантів у тебе вийшло?
Скільки різних варіантів у тебе вийшло?
- Не переставляючи цифри в лівій частині рівності, постав між ними два знаки «+», щоб вийшли вірні рівності.
|
1) 8 |
7 |
8 |
9 |
9 |
2 |
4 = 1010 |
|
2) 7 |
8 |
7 |
8 |
7 |
8 |
7 = 1672 |
|
3) 9 |
3 |
8 |
4 |
5 |
6 |
9 3 = 1676 |
|
4) 4 |
5 |
4 |
5 |
4 |
5 |
4 = 913 |
- Прочитай завдання.
Дано число 2718. Запиши всі можливі чотирицифрові числа, переставляючи цифри даного числа. Для цього розгадай правило, за яким складено перший стовпчик чисел. Користуйся способом перебору і запиши числа в інших стовпчиках.
|
2718 |
7 |
1 |
8 |
|
2781 |
|
|
|
|
2178 |
|
|
|
|
2187 |
|
|
|
|
2871 |
|
|
|
|
2817 |
|
|
|
- Заповни дерево можливих варіантів для чисел, в яких 7 тисяч
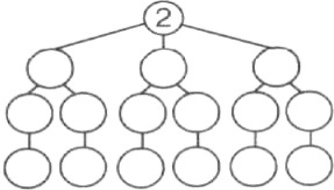 Схема 1 Одиниці тисяч Сотні
Схема 1 Одиниці тисяч Сотні
Десятки
![]() Одиниці
Одиниці
Скільки варіантів у тебе вийшло?
![]()
![]() Заповни дерево можливих варіантів для чисел, в яких 1 тисяча
Заповни дерево можливих варіантів для чисел, в яких 1 тисяча
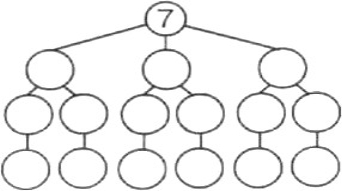 Одиниці тисяч Сотні
Одиниці тисяч Сотні
![]() Десятки Одиниці
Десятки Одиниці
Скільки варіантів у тебе вийшло?
- Здогадайся ! Скільки можна записати чисел, в яких 8 тисяч?
-
 Скільки всього можна записати чотирицифрових чисел, переставляючи цифри в числі 2718?
Скільки всього можна записати чотирицифрових чисел, переставляючи цифри в числі 2718?
24.
![]()
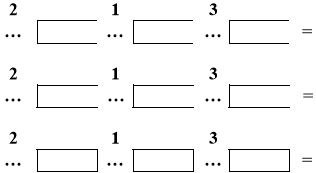
![]() 1. Постав знаки арифметичних дій, якщо вказано порядок їх виконання.
1. Постав знаки арифметичних дій, якщо вказано порядок їх виконання.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
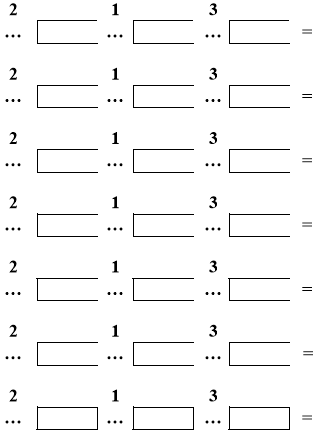
![]()
![]()
![]()
![]()
![]()
![]() Скільки різних варіантів у тебе вийшло?
Скільки різних варіантів у тебе вийшло?
3. Постав у віконця числа знайди значення виразів.
25.
- Прочитай задачу.
В одному з відділів «Дитячого світу» продавали плетені речі: шарфи – чорні (Ч) і бордові (Б); берети – жовті (Ж) , зелені – (З), сині (С), рукавички – голубі (Г), рожеві (Р).
Скільки комплектів з трьох речей можна скласти?
- Заповни кожну схему (дерево можливих варіантів) і порівняй отримані результати.
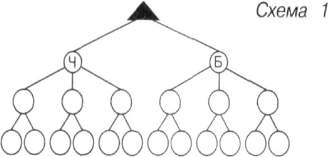 Шарфи Берети
Шарфи Берети
рукавиці
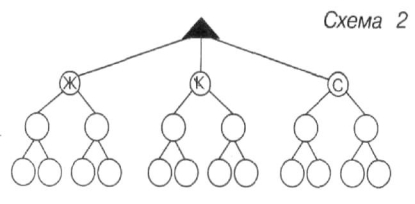
![]() Скільки отримали комплектів із трьох речей?
Скільки отримали комплектів із трьох речей?
Берети Шарфи Рукавиці
![]()
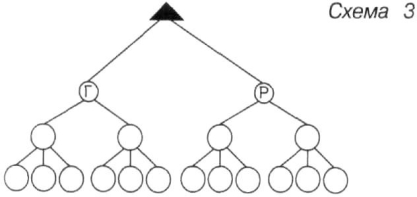
![]()
![]() Скільки отримали комплектів із трьох речей?
Скільки отримали комплектів із трьох речей?
![]() Рукавиці Шарфи берети
Рукавиці Шарфи берети
Скільки отримали комплектів із трьох речей?
- Обведи зеленим кольором гілочки на схемах, які позначають комплекти, в які входять жовті берети.
-



Користуючись умовними позначеннями, випиши можливі варіанти складання комплектів з трьох речей.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Випиши комплект, який тобі сподобався найбільше
![]()
26.
- Прочитай задачу.
Скільки різних чотирицифрових чисел можна записати, використовуючи цифри 6,5,2.
- Для відповіді на запитання задачі заповни частину схеми дерева можливих варіантів.
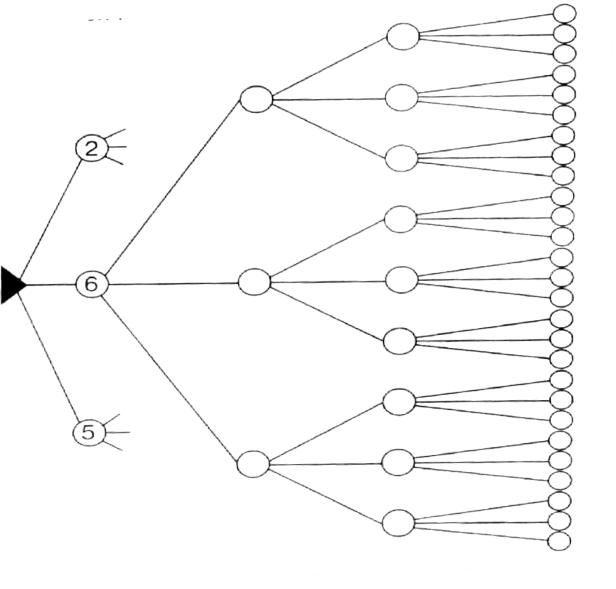 Одиниці тисяч сотні десятки одиниці
Одиниці тисяч сотні десятки одиниці
-
 Скільки чотирицифрових чисел, в яких 6 тисяч, можна записати цифрами 6,5,3?
Скільки чотирицифрових чисел, в яких 6 тисяч, можна записати цифрами 6,5,3?
- Догадайся! Скільки чотирицифрових чисел можна записати цифрами 6,5,2 якщо в цих числах
![]() а) 2 тисячі
а) 2 тисячі
![]() б) 5 тисяч
б) 5 тисяч
- Запиши відповідь на запитання задачі:
![]()
- Використовуючи схему – дерево можливих варіантів
запиши всі числа, в яких
а) 65
сотень б) 25
сотень в) 625
десятки г) 252
десятки
-
 Скільки чотирицифрових чисел можна записати цифрами 5,6,2 якщо в розряді одиниць стоїть цифра 2?
Скільки чотирицифрових чисел можна записати цифрами 5,6,2 якщо в розряді одиниць стоїть цифра 2?
- Обведи на схемі зеленим кольором гілку, на якій записане найбільше чотирицифрове число.
27.
- Прочитай задачу.
Скільки чотирицифрових чисел можна записати цифрами 3,4,8, якщо в розряді десятків стоїть цифра 3 і цифри в цих числах можуть повторюватись?
- Заповни схему – дерево можливих варіантів.
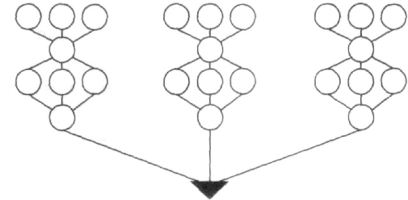 Одиниці Десятки Сотні
Одиниці Десятки Сотні
Одиниці тисяч
![]() Скільки отримали чотирицифрових чисел?
Скільки отримали чотирицифрових чисел?
- а) обведи червоним кольором гілки дерева, які позначають чотирицифрові числа, в яких 8 сотень.
б) Обведи зеленим кольором гілки дерева, які позначають чотирицифрові числа, в яких три однакові цифри;
в) Використовуючи дерево можливих варіантів, запиши чотирицифрові числа, в записі яких використовуються тільки цифри 3 і 4.
28.
- Прочитай задачу.
![]() Скільки чотирицифрових чисел, в яких 3 тисячі, можна записати цифрами 5,0,3?
Скільки чотирицифрових чисел, в яких 3 тисячі, можна записати цифрами 5,0,3?
- Заповни схему – дерево можливих варіантів.
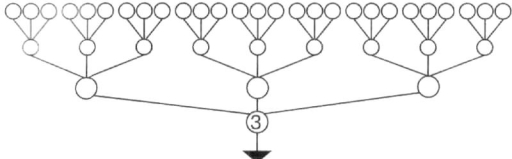
![]() Скільки отримали чотирицифрових чисел?
Скільки отримали чотирицифрових чисел?
- Запиши, скільки вийде чотирицифрових, записаних цифрами 3, 0, 5 в яких в розряді сотень цифра 0.
- Скільки отримаємо чотирицифрових чисел, в запису яких використовують ті ж цифри, але в розряді сотень – цифра 5?
29. Не переставляючи цифри в лівій частині рівності, постав між ними знаки арифметичних дій і дужки так, щоб отримати правильні рівності.
|
а) 1 |
2 |
3 = 1 |
|
|
|
б) 1 |
2 |
3 |
4 = 1 |
|
|
в) 1 |
2 |
3 |
4 |
5 = 1 |
|
30. |
|
|
|
|
- Прочитай задачу і спробуй відповісти на запитання, не використовуючи малюнка.
а) Скільки варіантів вибору двох олівців із трьох олівців різного кольору?
б) Скільки варіантів вибору двох олівців із чотирьох олівців різного кольору?
в) Скільки варіантів вибору двох олівців із п’яти олівців різного кольору?
г) Скільки варіантів вибору двох олівців із шести олівців різного кольору?
д) Скільки можна накреслити відрізків, якщо дано чотири точки, що не лежать на одній прямій?
ж) Скільки можна накреслити відрізків, якщо дано п’ять точок, що не лежать на одній прямій?
з) Скільки можна накреслити відрізків, якщо дано три точки, що не лежать на одній прямій?
- Випиши номери задач, в яких отримали однакові відповіді:
це _і ; це і _ ; це _і ; це і _ ;
- Подумай і поясни, чому в цих задачах вийшли однакові відповіді.
З М І С Т
|
1. Передмова |
- 5 |
|
2. Методичні рекомендації |
- 6 |
|
3. Комбінаторні задачі |
- 7 |
|
4. Список використаної літератури |
- 54 |
Л І Т Е Р А Т У Р А
- Афанасьєва О. М., Бродський Я. С., Павлов О. Л., Сліпенько А. К. Математика: Підручник. – Київ: Вища школа, 2001. – 447 с.
- Богданович М. В. Математика: підручник для 1 кл. – Київ: Освіта, 2002. - 128 с.
- Богданович М. В. Математика: підручник для 2 кл. – Київ: Освіта, 2002. - 160 с.
- Богданович М. В. Математика: підручник для 3 кл. – Київ: Освіта, 2003. - 160 с.
- Богданович М. В. Математика: підручник для 4 кл. чотириріч. І 3 кл. триріч. поч. шк. – 3-тє вид. – Київ: Освіта, 1998. - 240 с.
- Богданович М. В. та ін. Методика викладання математики в початкових класах: Навчальний посібник. – Київ: А. С. К., 1998. – 352 с.
- Єжов І. І., Скороход А. В., Ядренко М. Й. Елементи комбінаторики. – Київ: Вища школа, 1972. – 84 с.
- Друзь Б. Г. Творчі вправи з математики для початкових класів. – Київ: Рад. шк., 1988. – 144 с.
- Кружель О. В. Елементи теорії множини і математичної логіки. Посібник для самоосвіти вчителів. – Київ: Рад. шк., 1977.


про публікацію авторської розробки
Додати розробку