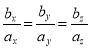Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами.
Тема уроку. Вектори в просторі (рівність векторів, колінеарність векторів, компланарність векторів). Додавання, віднімання векторів, множення вектора на число, властивості дій над векторами.
Мета уроку: формування знань учнів про вектори в просторі, дії над векторами, заданими координатами, Формування вмінь застосовувати вивчений матеріал до розв'язування задач.
Обладнання: схема «Вектори в просторі».
Хід уроку
І. Перевірка домашнього завдання
I. Перевірити правильність виконання задачі № 63 за заготовленими
 записами на дошці.
записами на дошці.
Розв'язання задачі № 63
Нехай SO ![]() α,
α, ![]() SAO = 45°,
SAO = 45°, ![]() OAB = 45° (рис. 292). Проведемо SO
OAB = 45° (рис. 292). Проведемо SO ![]() ОА. Нехай SO = а; тоді ОА = а, OB = a. ΔOSA = ΔOSB = ΔОАВ (за двома катетами). Із рівності трикутників випливає, що SA = SB = AB, тобто ΔSAB — рівносторонній; отже,
ОА. Нехай SO = а; тоді ОА = а, OB = a. ΔOSA = ΔOSB = ΔОАВ (за двома катетами). Із рівності трикутників випливає, що SA = SB = AB, тобто ΔSAB — рівносторонній; отже, ![]() SAB = 60°.
SAB = 60°.
Відповідь. 60°.
II. Сприйняття й усвідомлення нового матеріалу
 Учням пропонується прочитати в підручнику п. 35 і 36 і познайомитися з векторами в просторі та діями над векторами в просторі.
Учням пропонується прочитати в підручнику п. 35 і 36 і познайомитися з векторами в просторі та діями над векторами в просторі.
Далі пропонується фронтально обговорювати запитання та виконувати додаткові завдання.
1. Що таке вектор? Що таке абсолютна величина вектора? Які вектори називаються однаково напрямленими? протилежно напрямленими?
Завдання.
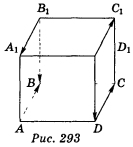
 а) Укажіть однаково напрямлені, протилежно напрямлені вектори серед векторів, які вказані на зображенні прямокутного паралелепіпеда (рис. 293).
а) Укажіть однаково напрямлені, протилежно напрямлені вектори серед векторів, які вказані на зображенні прямокутного паралелепіпеда (рис. 293).
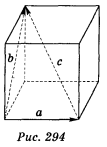
б) Знайдіть |![]() |, |
|, |![]() |,|
|,|![]() | (рис. 294), якщо на рисунку зображено куб з ребром 5 см.
| (рис. 294), якщо на рисунку зображено куб з ребром 5 см.
2. Які вектори називаються рівними? протилежними?
Завдання.
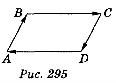 а) ABCD — паралелограм (рис. 295). Які векторні рівності можна записати?
а) ABCD — паралелограм (рис. 295). Які векторні рівності можна записати?
б) Чи можлива рівність векторів АВ і ВА ?
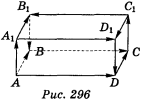 в) Укажіть рівні і протилежні вектори, якщо на рис.296 зображено прямокутний паралелепіпед.
в) Укажіть рівні і протилежні вектори, якщо на рис.296 зображено прямокутний паралелепіпед.
3. Дайте означення координат вектора з початком у точці А (а1; а2; а3) і кінцем у точці В (b1; b2; b3). Яка умова рівності векторів, заданих координатами?
Завдання.
а) Дано точки А (2; 3; 4), B(1; 1; 1). Які координати векторів ![]() ,
, ![]() ?
?
б) Які координати вектора ![]() , якщо А (5; 1; -3), точка О – початок координат?
, якщо А (5; 1; -3), точка О – початок координат?
в) Коли вектор ![]() (1; 2; 3) відклали від початку координат, то дістали вектор ОА. Які координати точки А?
(1; 2; 3) відклали від початку координат, то дістали вектор ОА. Які координати точки А?
г) Знайти |![]() |, якщо А (1; 2; 3), В (3; 2; 1).
|, якщо А (1; 2; 3), В (3; 2; 1).
д) Дано точки А(3; -2; 5), В(-4; 6; 1), С(-2; - 6; -11), D(х; у; z). Знайдіть х, у, z, якщо ![]() .
.
е) Абсолютна величина вектора ![]() (5; 3; z) дорівнює 9. Знайдіть z.
(5; 3; z) дорівнює 9. Знайдіть z.
4. Що називається сумою (різницею) векторів ![]() (аx; аy; аz) і
(аx; аy; аz) і ![]() (bx; by; bz)? Яка умова належності точок А, В, С прямій?
(bx; by; bz)? Яка умова належності точок А, В, С прямій?
Завдання.
а) Дано вектори ![]() (4; -5; 6),
(4; -5; 6), ![]() (-1; 2; 5). Знайдіть:
(-1; 2; 5). Знайдіть: ![]() +
+![]() ,
, ![]() –
– ![]() , |
, |![]() +
+ ![]() |, |
|, |![]() –
– ![]() |.
|.
б) Чи лежать на одній прямій точки А, В, С, якщо А(3; -7; 8), В(-5; 4; 1), С (27; -40; 29)?
в) Знайдіть координати точки С такої, що СА + СВ = 0, якщо А(-5; 7; 12), В(4; -8; 3).
г) Знайдіть координати векторів ![]() і
і ![]() , якщо
, якщо ![]() =
= ![]() +
+ ![]() ,
, ![]() =
= ![]() –
– ![]() ,
, ![]() (4; -1; 5),
(4; -1; 5), ![]() (6; 3; 1).
(6; 3; 1).
д) Чи може бути нульовим вектором сума трьох векторів, модулі яких дорівнюють 7; 1; 8?
е) Спростіть: ![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() ;
; ![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() .
.
5. Що називається добутком вектора ![]() (аx; аy; аz) на число λ? Які вектори називаються колінеарними? Яка умова колінеарності ненульових векторів?
(аx; аy; аz) на число λ? Які вектори називаються колінеарними? Яка умова колінеарності ненульових векторів?
Завдання.
а) Дано ![]() (1; -2; 3),
(1; -2; 3), ![]() (-2; 1; -3). Знайдіть координати векторів 2
(-2; 1; -3). Знайдіть координати векторів 2![]() ; - 3
; - 3![]() ; 2
; 2![]() + 3
+ 3![]() ; 2
; 2![]() - 3
- 3![]() .
.
б) Знайдіть |2![]() |, якщо
|, якщо ![]() (1; 2; 2).
(1; 2; 2).
в) Чи колінеарні вектори ![]() (2; 3; 8) і
(2; 3; 8) і ![]() (-4; 6; - 16) ?
(-4; 6; - 16) ?
г) При якому значенні т і п вектори ![]() (15; т; 1) і
(15; т; 1) і ![]() (18; 12; п) колінеарні?
(18; 12; п) колінеарні?
д) Чи колінеарні вектори АВ і CD, якщо А(3; -2; 5), B(-1; 4; 7), C(1; 3; 6), D(-3; 9; 18)?
е) При яких значеннях т і п вектори АВ і CD колінеарні, якщо A(1; 0; 2), B(3; n; 5), C(2; 2; 0), D(5; 4; m)?
6. Три вектори називають компланарними, якщо відповідні їм напрямлені відрізки розміщені в паралельних площинах. Вектори ![]() ,
, ![]() і
і ![]() компланарні тільки за умови, що точки О, А, В, С лежать в одній площині.
компланарні тільки за умови, що точки О, А, В, С лежать в одній площині.
Завдання.
а) Чи компланарні вектори ![]() (3; 2; 0),
(3; 2; 0), ![]() (6; 3; 0),
(6; 3; 0), ![]() (8; 1; 0)?
(8; 1; 0)?
б) ABCD — тетраедр, К, Р, Т — середини його ребер АВ, АС і AD. Чи компланарні вектори ![]() ,
, ![]() і
і ![]() ;
; ![]() ,
, ![]() і
і ![]() ?
?
III. Домашнє завдання
§ 4, п. 35—36; контрольні запитання № 18—20; задачі № 51—53 (с. 58).
IV. Підведення підсумку уроку
Підведення підсумку уроку доречно провести з використанням даної схеми.
Вектори в просторі^т: :••:•;' '/і-'ргй'ї:'. '•. '• {^: у '.•?":•: ••':?': ї:':':^''.":;'::^':^, '.':'•"• '.';Sї^::•:";:^;:•^'"'i*^W?Rll.ЩЩ^;;^^•;^^HЛ<.ll^^^^^ ^•:•^^^f^^y.^^:•::f^.:?:ї'•^^л.^\\'\•v^f:^.їл^v^^.'^fк^i
|
|
|
|
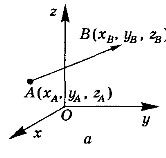
Координати вектора (рис. а)
|
Довжина вектора
|
|
Рівність векторів
|
|
|
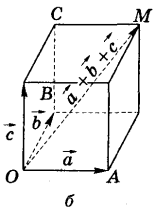
Сума векторів (рис. б)
|
|
|
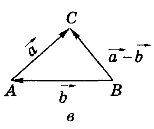
Різниця векторів (рис. в)
|
|
Добуток вектора на число
λ· |
|
Колінеарні вектори
|
|


про публікацію авторської розробки
Додати розробку