Тема уроку. Розв'язування задач на застосування векторів.

Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв'язування задач.

Обладнання: стінна таблиця "Вектори в просторі».

Хід уроку

І. Перевірка домашнього завдання

1. Два учні відтворюють розв'язування задач № 55 (4), 56.

2. Фронтальне опитування.

1) Чому дорівнює скалярний добуток векторів, які задано коорди­натами?

2) Як можна обчислити скалярний добуток векторів, якщо відомі їх довжини і кут між ними?

3) Як можна визначити косинус кута між двома ненульовими век­торами?

4) Сформулюйте ознаку перпендикулярності двох ненульових векторів.

5) У просторі дано вектори (1; 1; 0), (0; 1; 1). Укажіть, які з вказаних тверджень правильні, а які — неправильні:

а) довжини векторів і рівні;

б) скалярний добуток векторів і дорівнює 2;

в) кут між векторами і дорівнює 120°;

г) ( + )( – ) = 0;

д) вектори + і – перпендикулярні.

3. Перевірити правильність виконання задач № 55 (4), 56 учнями на дошці та відповісти на запитання, які виникли в учнів класу в ході виконання домашніх завдань.

II. Закріплення та осмислення знань учнів

Розв'язування задач

1. Знайдіть довжину діагоналі АС паралелограма ABCD, якщо А (2; - 6; 0),        В (-4; 8; 2), D (0;-12;0).

Розв'язання

Оскільки (- 6; 14; 2), (-2; -6; 0), то = + , AC (-8; 8; 2)

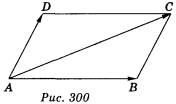(рис. 300).

Тоді = = = 2. Відповідь. 2.

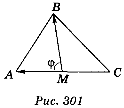2. Знайдіть кут між стороною АС і медіаною ВМ трикутника АВС, якщо А(-3; -5; 1), В(-4; -1; -2) і С(3; 3; 1).

Розв'язання

Кут між стороною АС та медіаною ВМ дорівнює куту φ між векторами та (рис. 301), або, якщо кут між цими векторами тупий,— куту 180° – φ.

Знайдемо координати точки М: М = М (0; -1; 1).

Тоді (-4; 0; -3), (-3; -4; 0);

cos φ =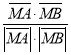==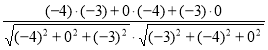  . φ = arccos — гострий кут. Отже, кут між стороною АС та медіаною ВМ дорівнює arccos . Відповідь. arccos .

3. Обчисліть площу паралелограма, побудованого на векторах  (3; 0; -4) і (0; 5; 0).

Розв'язання                              

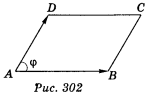Нехай паралелограм ABCD побудований на векторах AB і AD (рис. 302). Площа паралелограма дорівнює добутку суміжних сторін на синус кута між ними:  S = · · sin φ.

= = 5; = = 5;

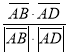cos φ = = = 0 .

Оскільки cos φ = 0 , то φ = 90° . Тоді sin φ = 1 і S = 5 · 5 · 1 = 25.

Відповідь. 25.

4. Задача № 58* із підручника (с. 58).

5. Задача № 61* із підручника (с. 59).

6. Задача № 62* із підручника (с. 59).

III. Домашнє завдання

Розв'язати задачі № 57*, 60 (с. 58—59) та підготуватися до тематич­ної атестації № 6.

IV. Підведення підсумку уроку

У ході фронтальної бесіди з'ясувати алгоритм застосування векторів до розв'язування задач.