Вибрані питання розв'язування завдань з параметрами (підготовка до ЗНО)

УПРАВЛІННЯ ОСВІТИ ШЕПЕТІВСЬКОЇ МІСЬКОЇ РАДИ

МЕТОДИЧНИЙ КАБІНЕТ

 

 

 

 

 

Вибрані питання

розв’язування завдань з параметрами

 

 

 

 

 

 

Автор-укладач

Строюк Марина Борисівна

вчитель математики,

спеціаліст вищої категорії

Шепетівського навчально-виховного

комплексу №1 ім. Героя України

М.Дзявульського

Хмельницької області

 

 

 

 

 

2017

Рекомендовано науково-методичною радою управління освіти

Шепетівської міської ради (протокол №1/4 від 24.11.2017 р.)

Рецензенти:

Коновалова Г.А. – методист Шепетівського навчально-виховного комплексу №1 ім.Героя України М.Дзявульського

Автор Строюк М.Б. Вибрані питання розв’язування завдань з параметрами. – Шепетівський НВК №1, 2018 – 25 с.

 

У посібнику розглядаються деякі найбільш поширені методи розв’язування задач з параметрами, що пропонуються випускникам на ЗНО з математики. До всіх задач надаються розв’язки з повним обґрунтуванням.

Посібник розрахований на вчителів математики, випускників шкіл та учнів, що цікавляться розв’язуванням нестандартних задач з математики, що містять параметри.

 

 

 

 

 

 

 

 

 

 

 

 

© Строюк М.Б., 2018

Зміст

Вступ            4

РОЗДІЛ І Розв’язування завдань з параметрами для всіх можливих значень параметра                                                                                                                                                                        6

РОЗДІЛ ІІ Знаходження розв’язків завдань з параметрами, на які накладаються певні умови              13

РОЗДІЛ ІІІ  Графічний спосіб розв’язування завдань з параметрами  23

Література 29

ВСТУП

Задачі з параметрами сприяють формуванню  інтелектуальних умінь, розвитку логічного  мислення і математичної  культури, та їх розв’язування пов’язане зі значними труднощами. Це пов’язане з тим, що кожна задача з параметрам , передбачає розв’язування не однієї, а цілої низки різноманітних математичних задач: рівнянь, нерівностей тощо.

Працюючи з параметром слід пам’ятати про його двояку природу. З одного боку слід сприймати параметр як число, а з  іншого – як невідоме, поведінку якого слід передбачити і врахувати при отриманні розв’язку задачі. Наприклад при добуванні кореня парного степеня, при діленні на вираз, що містить параметр потрібно проводити додаткові дослідження, що впливатимуть на остаточну відповідь.

В шкільному курсі математики знайомство з параметрами починається у 7 класі при розв’язуванні лінійних рівнянь, згодом у 8-9 класах розв’язуванню задач з параметрами виділяються години лише у класах з поглибленим вивченням математики. За відсутності належної кількості годин учителю не завжди вдається  познайомити учнів з методами і прийомами розв’язування задач з параметрами, сформувати уміння і навички роботи з таким видом задач.

У старшій школі зустріч з параметром відбувається ще рідше: у деяких видах рівнянь та нерівностей, при обчислення площ фігур, тощо. Таким чином випускник школи обираючи математику при складанні ЗНО, зустрічається з проблемою при розв’язуванні задач з параметрами.

З чого розпочати розв’язування задач з параметрами? В першу чергу потрібно звести рівняння до більш простішого: розкласти на множники, врахувати область визначення, позбавитися модуля, логарифма, тригонометричних виразів, потім необхідно розв’язати окремо кожне із завдань.

При розв’язуванні завдань з параметром зустрічаються завдання, що можна поділити на такі  категорії: розв’язати рівняння або нерівність, їх системи для всіх можливих значень параметра; завдання, в яких пропонується знайти лише ті розв’язки, що задовольняють певним умовам. Третій тип завдань – визначити кількість коренів рівняння в залежності від значень параметра. Цей тип завдань в більшості випадків зручно і доречно розв’язувати графічним способом.

У збірнику запропоновано розв’язки завдань з параметрами, що пропонувалися на ЗНО з 2010 по 2017 рік. Розглянуто різні способи та прийоми розв’язування таких завдань.

РОЗДІЛ І

Розв’язування завдань з параметрами для всіх можливих значень параметра

1.     Розв’яжіть рівняння для всіх значень параметра а

.

Розглянемо область допустимих значень рівняння

Отже, враховуючи,що , тоді

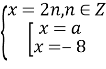
Відповідь: якщо а – парне, то рівняння має два розв’язки і ;

якщо а – непарне, то рівняння має один  розвозок  і .

2.     Розв’яжіть рівняння для всіх значень параметра а

 

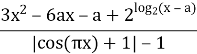
Врахувавши область визначення отримаємо систему рівнянь та нерівностей:

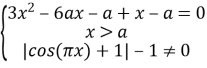
Оскільки то

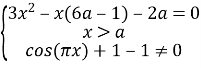
Розв’яжемо перше рівняння системи

Повернемося до системи:

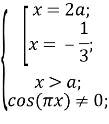
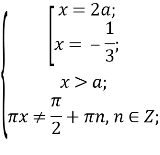
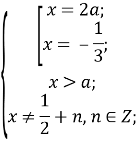
Перевіримо,при якому значенні параметра а існуватиме корінь .

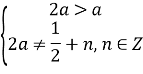
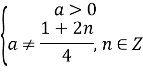
Перевіримо,при якому значенні параметра а існуватиме корінь .

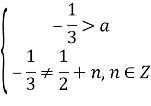
Отже, а, тоді .

Відповідь: якщо ), то ;

якщо , то ;

якщо )  і , то

3.  Розв’яжіть рівняння для всіх значень параметра а

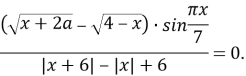
Врахувавши область визначення отримаємо систему рівнянь та нерівностей:

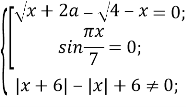
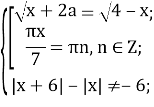
Розв’яжемо третє рівняння системи:

               

                                         

Повернемося до системи:

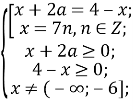
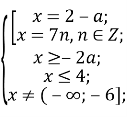
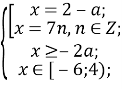
Оскільки задовольняє умову , то х=0 при =0. Тоді

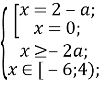
Перевіримо, при якому значенні параметра а існуватиме корінь x=2-а:

Отже, якщо а∈ [-2;8), то x=2-а. Корінь х=0 задовольняє умову а умову, при а0.

Відповідь: якщо a∈(-∞;-2), то x;

якщо a∈[-2;0), то x=2-a;

якщо a∈[0;8), то x=2-a, x=0;

якщо a∈[8;+ ∞), то x=0.

4. Розв’яжіть нерівність  для всіх значень параметра а

 

Знайдемо область визначення рівняння:  .

Піднесемо обидві частини нерівності до квадрату:

При піднесенні обох частин нерівності до квадрату слід врахувати два випадки:

                       

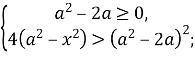
Оскільки а≠0, то                                       

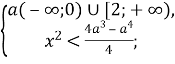
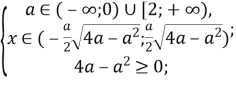
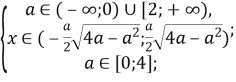
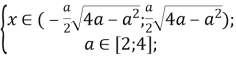
Відповідь: якщо a∈(-∞;0],  то x∈∅;

якщо a∈(0;2), то x∈(-a;a);

якщо a∈[2;4], то.

5. Розв’яжіть систему рівнянь  для всіх значень параметра а

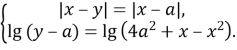
Розкривши модуль отримаємо сукупність двох систем:

                                  

Оскільки умова суперечить   то друга система не має розв’язку.

              

 

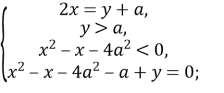
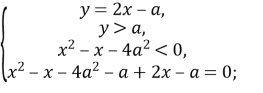
Розв’яжемо третю нерівність системи:    

 

  ;

  .               

Розв’яжемо  четверте рівняння системи:

 

Повернемося до системи:

  ;

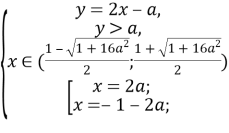Оскільки    і , тоді   , .

Перевіримо, при яких значеннях параметра а корені  та задовольняють умову .

                                         

                                         

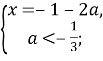
Повернемося до систем:

 

 

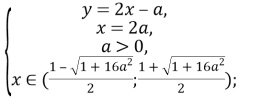
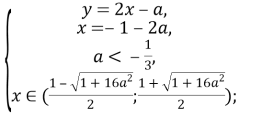
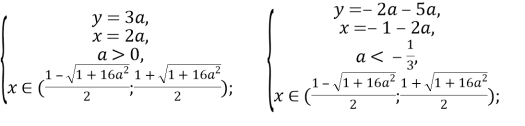
Відповідь: якщо a∈(-∞;),  то x=;;

якщо a∈[;0], то x∈∅; y=∈∅;

якщо a∈(0; +∞), то x=,  .

 

Розділ ІІ 

Знаходження розв’язків завдань з параметрами, на які накладаються певні умови

1. При яких значеннях параметра а рівняння має чотири корені

Введемо заміну     =t, t>0.

Оскільки t>0, то , a>0. Повернемося до заміни:=a. Використаємо формулу квадрата двочлена   =, отримаємо=a.

                                                   =a;

Розкриємо модуль:

                           

    

 

              

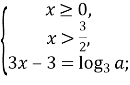
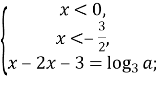
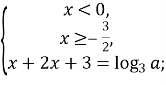
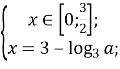
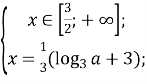
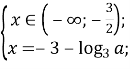
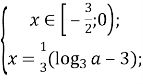
Перевіримо при яких значеннях параметра а отримані корені задовольняють умови:

0          

-3     ;     -             

            ;                        

a27;              ;                                     a<27.

                                                                   

 

 

 

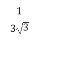
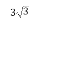
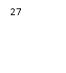
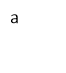
Відповідь: .

2. При якому значенні параметра а корінь рівняння належить проміжку (

Врахуємо область визначення рівняння:

Отримаємо, ,     n∈Z,  .

Оскільки , то

Звідси виплаває, що =4, тоді Знайдемо значення параметра, при якому .Оскільки  , і =0, то

Відповідь: .

3. Знайдіть найменше значення параметра а, при якому рівняння має додатній корінь

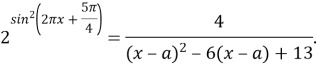
Прологарифмуємо обидві частини рівняння з основою 2:

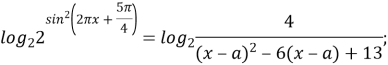
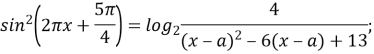
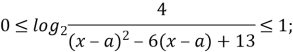
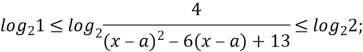
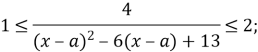
Оскільки     (D<0), то

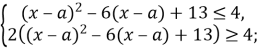
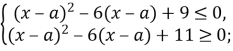
Отже,   то   тоді ;

Обчислимо значення х при     , ,

     , ,

, .

Знайдемо найменше значення параметра а, при якому існує додатний корінь .

,                ,           

Відповідь: .

 

4. Знайдіть усі значення параметра а, при якому добуток коренів рівняння

 , дорівнює 8.

Введемо заміну , тоді отримаємо рівняння

якщо , то рівняння має два корені:

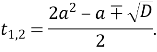
Повернемося до заміни    

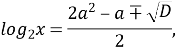
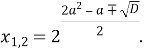
Обчислимо добуток коренів

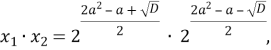
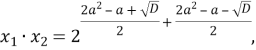
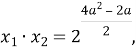
Оскільки добуток коренів дорівнює 8, то =8,

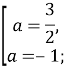
Врахувавши умову , отримаємо

Відповідь:

5. При якому найменшому а рівняння має хоча б один корінь

Введемо заміну

Оскільки  не задовольняє умову , тоді для існування хоча б одного кореня необхідно виконання умови

Відповідь:

6. Вкажіть найменше значення параметра, при якому рівняння має рівно один корінь  

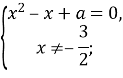
Розв’яжемо перше рівняння системи:

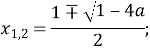
Отримаємо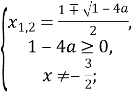

Рівняння матиме один корінь, якщо 0, при , тоді  .

Якщо ж , то рівняння має два корені     Для того, щоб рівняння мало рівно один корінь, один з розв’язків не повинен входити в область визначення рівняння, тому

                 

    

   

 

тже,  існує при , а   -  при   і .

Рівняння має рівно один корінь при   та .

Відповідь: .

7. При якому найменшому цілому значенні а рівняння має лише два різні корені

Рівняння рівносильне системі:

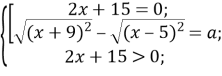
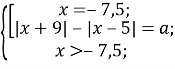
Розв’яжемо рівняння з модулем для всіх значень параметра а.

                

                                    

                                    

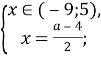
 При   та  при, рівняння має безліч розв’язків, тому розглядаємо випадок     ,   .

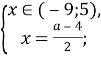
Повернемося до системи

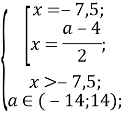
Врахуємо умову , та отримаємо обмеження на параметр а:

Отже, . Найменше ціле з цих значень

Відповідь: -10

8. Знайдіть найбільше значення  параметра а, при якому система має безліч розв’язків

Введемо заміну Отримаємо систему лінійних рівнянь відносно змінних і та параметра .

Розв’яжемо систему рівнянь способом додавання, домножимо перше рівняння на , отримаємо:

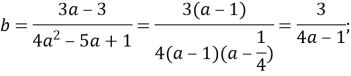
Повернемося до заміни:      

Оскільки , то

 

 

 

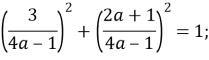
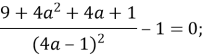
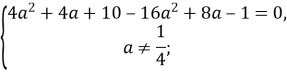
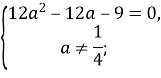
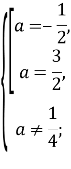
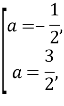
Найбільше значення параметра, при якому система має безліч розв’язків .

Відповідь: 1,5

РОЗДІЛ ІІІ

Графічний спосіб розв’язування завдань з параметрами

1. Знайдіть найбільше значення параметра а, при якому рівняння

  має тільки чотири корені.

Розглянемо функцію . Графіком функції є парабола, вітками направлена вгору, з вершиною у точці (1,5; -6,25). Нулі функції: х=4, х=-1.

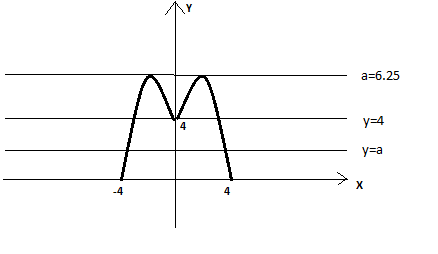Використовуючи геометричні перетворення графіка функції , отримаємо графік функції . Для визначення кількості коренів рівняння  , знайдемо точки перетину графіків функції  і =.

 

 

 

 

 

Використовуючи геометричну інтерпретацію розв’язків рівняння, отримаємо чотири розв’язки рівняння при i .

Відповідь: .

2. Знайдіть найбільше значення параметра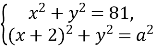, при якому система рівнянь має один розв’язок.

Графіком рівняння є коло з центром (0;0), радіус 9. Графіком другого рівняння. Оскільки система рівнянь має один розв’язок, кола дотикаються внутрішнім або зовнішнім способом, як показано на рисунку:

 

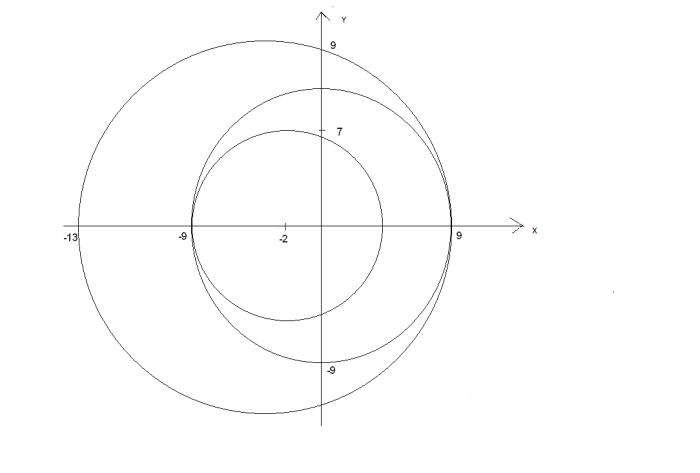Отже, система має один розв’язок при a=7, a=11. Найбільше значення a=11.

Відповідь: a=11.

3. Знайдіть усі значення параметра а, при якому система рівнянь має тільки три розв’язки.

Розв’язком першого рівняння є сукупність точок, що належать прямим , Графіком другого рівняння є коло з центром (0; 0) і радіусом . Оскільки система рівнянь має три розв’язки, то коло з центром (0; 0) і радіусом повинно перетинати пряму та дотикатися до прямої , як показано на рисунку:

 

 

 

 

 

 

 

 

 

 

 

 

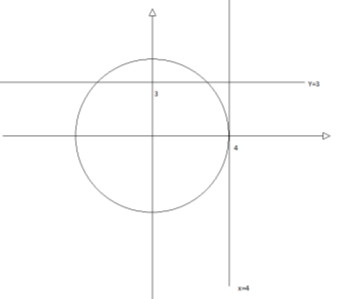
Отже, радіус кола дорівнює 4, тоді =4,

Відповідь:

4. При якому найбільшому від’ємному значенні параметра  a, рівняння , має один корінь.

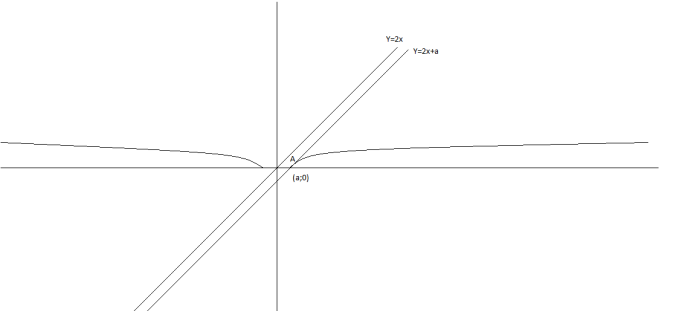Розглянемо рівняння . Кількість коренів рівняння визначимо графічно. Побудуємо графіки функцій , .

Рівняння має один розв’язок при найбільшому від’ємному значенні параметра а, якщо пряма дотикається до графіка функції . Знайдемо координати точки А – точки дотику.

Використаємо геометричний зміст похідної: , знайдемо, якщо .

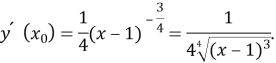
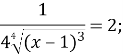
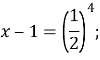
Знайдемо ординату точки А, якщо абсциса :

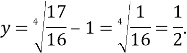
Оскільки А(; ), обчислимо значення параметра а з рівняння дотичної y=2x+a.

Відповідь:

5. Знайдіть усі від’ємні значення параметра 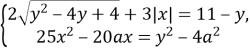, при яких система   має єдиний розв’язок.

Подамо систему рівнянь у вигляді:

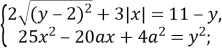
Побудуємо графік першого рівняння:

                                                       

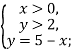
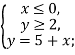
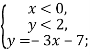
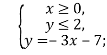
Графіком другого рівняння є сукупність прямих:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

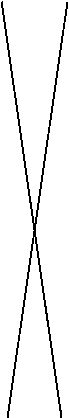
Отже, система має єдиний розв’язок, якщо прямі проходять через точку (-3; 2). Знайдемо значення параметра :

Відповідь:

Література

1. Апостолова Г.В., Ясінський В.В. Перші зустрічі з параметрами. – К.: Факт, 2008. – 324 с.

2. Апостолова Г.В. Хитромудрий модуль. К.: Факт, 2006. – 256 с.

3. Апостолова Г.В. Я сам! К.: Факт, 1997. – 202 с.

4. Горштейн П. І., Полонський В. Б., Якір М. С. Задачі з параметрами. – К.: РІА “Текст”; МП “ОКО”, 1992. – 290 с.

5. Назаренко О.М., Назаренко Л.Д. тисяча і один приклад. Рівності і нерівності. – Суми: “Слобожанщина”, 1994. – 272 с.

6. Фількенштейн Л. П. Домашній репетитор. Вибрані глави конкурсної математики в методах і задачах. Книга четверта. Параметри. – К.: Євро індекс Лтд, 1995. – 210 с.

7. Ястребинецький Г. А. Задачі з параметрами. – М.: Просвещение, 1986. – 128 с.

8. Лобанова Л. В., Фількенштейн Л. П. Вибрані задачі елементарної математики. – К: Вища школа, 1989. – 115 с.