Посібник "Математична скарбничка задач з комбінаторики"

 

Хухрянська ЗОШ І-ІІІ ступенів
Матеріал даного посібника можна використати для проведення уроків в 11 класі, а також для самоосвіти учнів, які бажають добре орієнтуватися в темі «Комбінаторика».

У посібнику міститься теоретичний матеріал, приклади з розв’язками, тестові завдання, приклади для виконання домашньої роботи, інтегрована вікторина, різнорівнева самостійна робота, контрольна робота, завдання для майбутнього абітурієнта.

 

МАТЕМАТИЧНА СКАРБНИЧКА ЗАДАЧ З КОМБІНАТОРИКИ

 

Актуальність:

• Комбінаторні задачі розвивають нестандартне мислення, уяву, логигу, смекалку.
• Задачі з комбінаторики включені на всіх етапах математичних олімпіад та ЗНО

    Комбінаторні задачі: навіщо вони потрібні?

      Якщо ви знаєте, що таке комбінаторні задачі, то ніяких складнощів з їх рішенням ви відчувати не будете. Методика їх вирішення може стати в нагоді при необхідності складання розкладів, графіків роботи, а також складних математичних обчислень, для виконання яких не підійдуть електронні пристрої.

Комбінаторика - наука майбутнього? Багато фахівців в області математики і фізики вважають, що саме комбінаторна задача може стати поштовхом у розвитку всіх технічних наук. Достатньо лише нестандартно підійти до вирішення тих чи інших проблем, і тоді можна буде відповісти на питання, які вже кілька століть не дають спокою вченим. Деякі з них всерйоз стверджують, що комбінаторика є підмогою для всіх сучасних наук, особливо космонавтики. Набагато простіше буде вираховувати траєкторії польоту кораблів з допомогою комбінаторних задач, також вони дозволять визначити точне знаходження тих чи інших небесних світил.

    Реалізація нестандартного підходу вже давно почалася в азіатських країнах, там учні навіть елементарні завдання по множенню, віднімання, складання і розподілу вирішують, використовуючи комбінаторні методи. На подив багатьох європейських вчених, методика дійсно працює. Школи Європи поки що тільки почали переймати досвід своїх колег. Коли саме комбінаторика стане одним з основних розділів математики, припустити складно. Зараз наука вивчається провідними вченими планети, які прагнуть популяризувати її.

 

 

 

 

 

 

 

 З задачами, в яких приходиться вибирати ті чи інші предмети, розміщувати їх в певному порядку і відшуковувати серед різних розміщень найкращі, люди стикнулися ще в доісторичну епоху, обираючи найкращі розміщення мисливців під час полювання, воїнів під час битви, інструментів під час роботи.

Пізніше, поряд із спортивними змаганнями з’явились ігри з різними фігурами чи предметами, в яких вигравав той, хто краще знав переможні комбінації та вмів уникати програшних.(Давня єгипетська гра «сенет», в яку грав фараон Тутанхамон, нарди, китайські та японські шахмати, японські шашки «го» і т. д.) Що ж було поштовхом до виникнення  комбінаторики, як науки? Для чого

ще потрібні знання з комбінаторики, крім відомого вже нам застосування в теорії ймовірності?

 

 

При вивченні розділу «Комбінаторика» в 11-му класі загальноосвітньої школи за програмою розглядають такі теми:

1.             Поняття множини. Елементи множини. Дії над множинами.
2.             Факторіал. Сполуки без повторень.
3.             Розв'язування комбінаторних задач
4.               Трикутник Паскаля. Біном Ньютона. Формула загального члена розкладу бінома.

 

 

 

Поняття множини

      Поняття множини належить до первісних, воно не означається. Множина — це сукупність, зібрання деяких предметів будь-якої природи, наприклад: множина учнів класу, множина цифр десяткової нумерації, множина букв українського алфавіту, множина міст держави, множина будинків на вулиці тощо.

    Для позначення множин використовуються прописні літери латинського алфавіту або фігурні дужки: множина А або {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Елементи множини

Означення. Предмети, з яких складається множина, називаються її елементами.

Наприклад, а = 5 — елемент множини цифр десяткової нумерації;

Львів — елемент множини міст України.

    Якщо множину цифр десяткової нумерації позначити через А, то належність числа цій множині можна позначити так:

 5  А, 9  А.

Число 12 не належить множині А, не є елементом цієї множини. Це твердження можна записати так: 12 А.

     Множини бувають скінченні (множина будинків а певній вулиці) і нескінченні (множина точок прямої).

Означення. Множина, у якій немає жодного елемента, називається порожньою.

Позначається .

Наприклад, множина розв'язків рівняння х² = -1 на множині дійсних чисел є порожньою.

    Множину можна задати: переліченням усіх її елементів, наприклад {а, b, с} або характеристичною властивістю, наприклад, В — множина чисел, кратних 15, що менші від 90.

Підмножина

Означення. Дві множини називаються рівними, якщо вони складаються з однакових елементів.

Наприклад, X — множина коренів рівняння x² = 25, Х = {-5; 5};

множина Y — множина коренів рівняння | х | = 5 , Y = {-5; 5}.

Х = Y.

Означення. Якщо множина В складається з деяких елементів даної множини А і лише з них, то множина В називається підмножиною множини А.

Позначається це так: В   А.

Наприклад, якщо В = {1, 2, 3}, А = {1, 2, 3, 4}, то В А.

 

 

 

 

 

     Над множинами можна виконувати певні операції. Розглянемо три з них.

 

Переріз множин

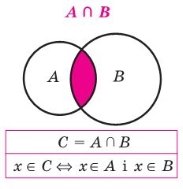Означення 5. Перерізом множин А і В називається множина С, яка складається з усіх тих і лише тих елементів, які належать кожній із даних множин.                             

Приклад 1. А — множина всіх дільників числа 32, В — множина всіх дільників числа 24.

А = {1, 2, 4, 6, 8, 16, 32}, B = {1, 2, 3, 4, 6, 8, 12, 24}.

С = А  В, С = {1, 2, 4, 8}.

 

 

Об'єднання множин

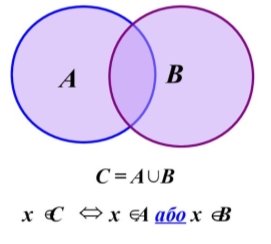Означення 6. Об'єднанням або сумою двох множин А і В називається така множина R, яка складається з усіх елементів множин А і В і лише з них.

Кожний зі спільних елементів береться в множину лише один раз.

Приклад. Для множин А і В з прикладу 1 об'єднанням буде

R = А    В = {1, 2, 3, 4, 6, 8, 12, 16, 24, 32}.

Приклад. Множина дійсних чисел є об’єднанням множин раціональних та ірраціональних чисел: Q  I = R.

Віднімання множин. Доповнення множини

Означення. Різницею двох множин А і В називається така множина D яка складається з усіх елементів множини А, які не належать множині В.

Записуємо D = А \ В.

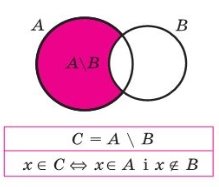
Приклад. А = {5, 6, 8, 12}, В = {5, 6}, D = {8,12}.

Приклад 5. А = {5, 6}, В = {5, 12, 6}, D =  {}.

Приклад. А = {2, 4, 5}, В = {2, 4}, DАВ = {5}.

 

Впорядкована множина

Означення 8. Скінченна множина, для якої істотний порядок елементів, називається впорядкованою.

Вказати порядок розміщення елементів у скінченній множині з n елементів — означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до n.

Приклад 7. Множини А = {1, 2, 7} і В = {2, 7, 1} є рівними, якщо вони не впорядковані, А = В.

Якщо ж вони є впорядкованими, то А ≠ В.

Приклад 8. Із 30 учнів класу потрібно вибрати двох:

а) старосту і його заступника;

б) для чергування у класі.

У випадку а) — це впорядкована множина.

Домашнє завдання.

1. Навести приклади для кожного сформульованого означення.
2. Знайти переріз множин М і Р, якщо М = {прості числа, менші від 40},        Р = {непарні числа, більші від 14}.
3. Знайти переріз, об'єднання і різницю множин К і L, якщо К = {1, 2, 3, 4, 5, 6, 7}, L = {2, 4, 6}.

 

 

 

 

 

Означення . Факторіал — це добуток послідовних натуральних чисел.

п! = 1 ∙ 2 ∙ 3  ∙ ... ∙ n.

Наприклад : 1! = 1;

2! = 1 ∙ 2 = 2;

3! = 1 ∙ 2 ∙ 3 = 6;

4! = 1 ∙ 2 ∙ 3 ∙ 4 = 3! ∙ 4 = 24.

Приймають, що 0! = 1.

Термін «факторіал» походить від англійського слова «фактор» — множник.

Вправи

1. Обчислити .

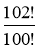Розв'язання

.

2. Спростити: а) 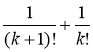; б) .

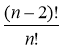Розв'язання

а) .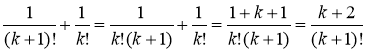

б) .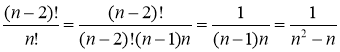

3. Розв'язати рівняння .

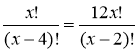Розв'язання

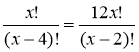
ОДЗ: х ≥ 4, х N.

,

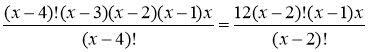(х – 3)(х – 2)(х – 1)х – 12(х – 1)х = 0,

(x – 1)x(x² – 5х – 6) = 0,

х – 1≠ 0, x ≠ 0; х² – 5х – 6 = 0;

х₁ = - 1, х₂ = 6. x₁ ОДЗ.

Відповідь. х = 6.

 

 

 

На практиці часто доводиться відповідати на запитання: скількома способами можна виконати певне завдання? Наприклад, скласти розклад п'яти уроків на день із десяти різних навчальних предметів; позначити різні зв'язки між атомами і молекулами певної речовини; записати діагоналі опуклого десятикутника; знайти різні шляхи доставки виробів із заводу в магазини і визначити, який з них найбільш вигідний.

Методи розв'язування таких задач вивчають у розділі математики, який називається комбінаторикою, а самі задачі — комбінаторними.

Розв'язуючи комбінаторні задачі, розглядають скінченні множини, утворені з елементів будь-якої природи, та їх підмножини. Залежно від умови задачі розглядаються скінченні множини, у яких істотним є або порядок елементів, або їх склад, або і те і те одночасно. Такі скінченні множини (сполуки) мають певну назву.

 

 

 

Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів.

Перестановки відрізняються одна від одної лише порядком елементів.

Приклад. Із елементів множини А = {1, 2, 7} можна утворити 6 перестановок: {1, 2, 7}, {1, 7, 2}, {2, 1, 7}, {2, 7, 1}, {7, 1, 2}, {7, 2, 1}.

Перестановки — впорядковані множини

Кількість усіх можливих перестановок у множині з п елементів позначається Р_n.

Обчислимо Р_п.

Один елемент можна розмістити одним способом: P₁ = 1.

Два елементи можна розмістити двома способами: Р₂ = 2.

Три елементи можна розмістити шістьма способами: Р₃ = 6.

Розглянемо множину з чотирьох елементів {а, b, с, d}. Із елементів цієї множини можна утворити такі перестановки: з першим елементом а — 6 перестановок: {а, b, с, d), {а, b, d, с), {а, с, b, d}, {а, с, d, b), {а, d, с, b}, {а, d, b, с};

з першим елементом b — 6 перестановок;

з першим елементом с — 6 перестановок;

з першим елементом d — 6 перестановок.

Усього 24 перестановки: Р₄ = 24.

Взагалі, кількість усіх можливих перестановок у множині з п елементів дорівнює добутку послідовних натуральних чисел, тобто

Р_n  = 1 ∙ 2 ∙ 3 ∙ 4 ∙ ... ∙ n,

Р_n = п!,      

де п — натуральне число.

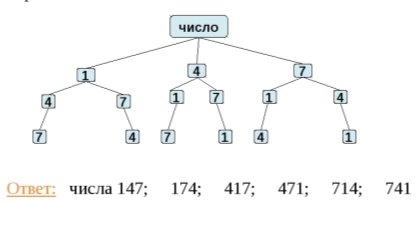    Дерево з варіантів.  Деякі комбінаторні задачі можна вирішити, лише складаючи схеми, в яких буде детально вказана інформація про кожен елемент. Складання дерева можливих варіантів - ще один спосіб знаходження відповіді. Він підходить для вирішення не дуже-то складних завдань, в яких є додаткова умова.

Задача. Розглянемо задачу про складання трьохзначних чисел з цифр 1, 4, 7 (цифри у запису числа не повторюються). Для її розв’язку строять схему-дерево можливих варіантів

Приклад. 12 осіб можна розмістити за столом, біля якого поставлено 12 стільців, Р_І2= 12! способами.

12! = 479 001 600. Якщо гості будуть пересаджуватися щохвилини протягом 11 годин на добу 365 днів на рік з відпочинком 1 день у високосному році, то на це піде 1988 років і 140 днів.

Приклад. Мандрівнику потрібно виїхати з пункту А, відвідати пункти В, С, й і повернутися в пункт А. АD = 500 км, СD = 400 км, ВD = 400 км, АВ = 300 км, АС — 200 км, ВС = 350 км. Скількома способами він може це зробити? Який варіант найбільш оптимальний?

Розв'язання

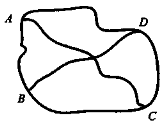Розглянемо схему руху мандрівника.

Оскільки йому потрібно відвідати три пункти, то можливих варіантів маршруту є 6: Р₃ = 3! = 6.

АВСDА = 1550 км, АСDВА = 1300 км, АВDСА = 1300 км, АDВСА = 1450 км, АСВDА = 1450 км, АDСВА = 1550 км.

Відповідь. Найбільш оптимальними є варіанти АВDСА і АСDВА.

Задача. Скількома способами можна скласти денний розклад з п'яти різних уроків, якщо в класі вивчають 10 навчальних предметів?

Розв'язання

. Отже, загальна кількість способів, за якими можна поставити два перших уроки, становить 10 ∙ 9 = 90.

Для третього уроку залишається Я можливостей вибору предмета, бо два вже поставлено в розклад. Тому для розподілу трьох Маємо 10 різних можливостей запису в розклад першого уроку, бо кожний предмет можна поставити першим уроком.

Другим уроком можна поставити будь-який з 9 предметів, що залишилися перших уроків кількість різних способів дорівнюватиме 10 ∙ 9 ∙ 8 = 720.

Для четвертого уроку залишається 7 можливостей вибору предметів, для п'ятого — 6, тому, щоб поставити п'ять уроків у розклад, існує 10 ∙ 9 ∙ 8 ∙ 7 ∙ 6 = = 30 240 різних способів.

Розв'язуючи задачу, ми з множини, що містить 10 елементів, утворювали впорядковані підмножини, що містять по одному, два, три, чотири, п'ять елементів, тобто утворювали розміщення з 10 елементів відповідно по одному, два, три, чотири, п'ять. Кількість усіх можливих розміщень з m елементів по n елементів позначається .

Ми з'ясували, що

= 10, = 10 ∙ 9, = 10 ∙ 9 ∙ 8, = 10 ∙ 9 ∙ 8 ∙ 7, = 10 ∙ 9 ∙ 8 ∙ 7 ∙ 6.

Аналізуючи закономірність утворення чисел , , , , . помічаємо, що:

• кожне з них дорівнює добутку стількох послідовних натуральних чисел, скільки елементів у розміщенні;
• на першому місці стоїть множник, що дорівнює кількості всіх елементів множини, з якої утворюються розміщення, а кожний наступний множник на одиницю менший від попереднього;
• останній множник дорівнює різниці між кількістю всіх елементів, з яких утворюється розміщення, і числом, на одиницю меншим від кількості
  елементів у розміщенні.

Припускаємо, що формула має вигляд:

= m (m – 1)(m – 2) … (m – (n – 1));

= m (m – 1)(m – 2) … (m – n + 1).   

      

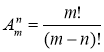
Доведення можна провести методом математичної індукції на факультативному занятті.

Означення. Будь-яка підмножина з п елементів даної множини М, що містить т елементів, називається комбінацією з т елементів по п.

Порядок елементів у множині неістотний, комбінації відрізняються лише складом елементів. Кількість усіх можливих комбінацій з т елементів по n позначається символом .

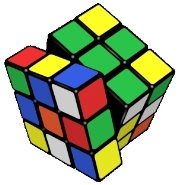Комбінація відрізняється від розміщення тим, що у цій підмножині неістотним є порядок елементів.

Задача. Скількома способами можна призначити чотирьох вартових із 30 солдатів?

Розв'язання

Будь-які дві групи відрізняються лише складом солдат, порядок у групі неістотний. Маємо справу з різними підмножинами з чотирьох елементів даної множини, що складається з 30 елементів. Будь-яка з цих підмножин є комбінацією з 30 елементів по 4. Якби ця підмножина була упорядкованою, то кількість таких груп можна знайти за формулою . У кожній з упорядкованих множин можна виконати Р₄ перестановок, тому кількість усіх можливих комбінацій .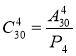

У загальному випадку кількість комбінацій з т елементів по л елементів можна обчислити за формулою:

      

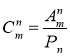
Перетворимо цю формулу, використавши формули 2 і 1.

.

.      

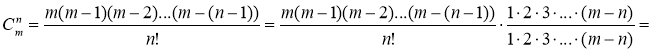
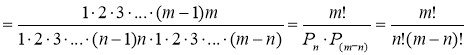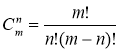Отже, чотирьох вартових із 30 солдатів можна вибрати 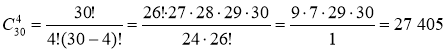способами.

Або за формулою 4: .

Властивості комбінацій

1. 
2. .
3. .

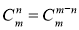
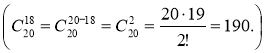
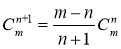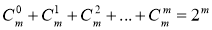Приклад. На площині позначено n точок, з яких ніякі три не лежать на одній прямій. Скільки різних прямих можна провести через ці точки?

Розв'язання

Оскільки через кожну пару точок можна провести лише одну пряму, то кількість різних прямих дорівнює кількості комбінацій з n елементів по 2 елементи, тобто .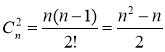

Домашнє завдання.

Розв'язати задачі

1. Скільки слід взяти елементів, щоб кількість усіх перестановок, які можна утворити з них, дорівнювала 5040?
2. Скільки різних прямих можна провести через 10 точок площини, з яких ніякі три не лежать на одній прямій?
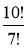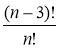3. Спростити вираз: а) ; б) ; в) .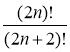

 

 

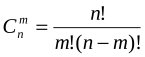
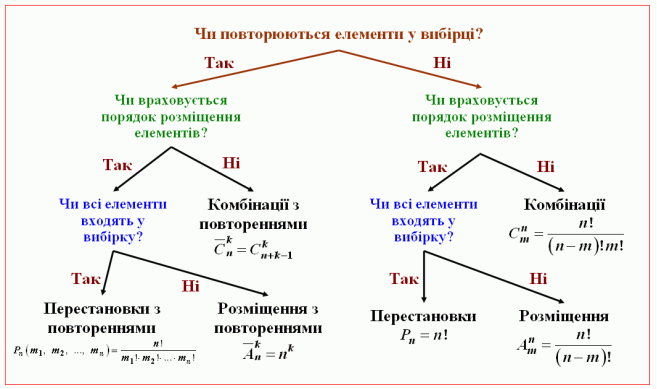
Вибір формули  чи 

 

 

1. Скільки семицифрових чисел можна утворити за допомогою семи різних цифр, відмінних від 0, не повторюючи цифри у запису числа?

Розв'язання

Шукане число дорівнює кількості перестановок із 7 різних елементів:

Р₇ = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5040.

Відповідь. 5040 різних семицифрових чисел.

2. Скільки можна утворити різних двоцифрових чисел із чотирьох цифр 1, 3, 7, 9, не повторюючи їх?

Розв'язання

Потрібно утворити впорядковані множини з двох елементів: 13, 31, 17, 71, ... . Ці множини є розміщеннями з 4 елементів по 2, тобто кількість усіх двоцифрових чисел, що відповідають умові, становитиме = 4 ∙ 3 = 12.

Відповідь.  12.

3. Скільки можна утворити різних трицифрових додатних цілих чисел у десятковій системі числення, не повторюючи цифри у запису числа?

Розв'язання

Із 10 цифр можна утворити = 10 ∙ 9 ∙ 8 = 720 різних трицифрових чисел. З них із цифри 0 починаються   = 9 ∙ 8 = 72 числа. Усього чисел, що відповідають умові, можна утворити – = 648.

Відповідь. 648 чисел.

4. Відомо, що старосту і його заступника в класі можна вибрати шістьмастами різними способами. Скільки учнів у класі?

Розв'язання

Позначимо кількість учнів у класі через де, (х — натуральне число). Шукана підмножина є впорядкованою, тому можна записати:

= 600.

х(х – 1) = 600;

х² – х – 600 = 0;

х₁ = 25 , х₂ = -24.

- 24 не відповідає умові задачі.

Відповідь. 25 учнів.

 

5. Розв'язати рівняння 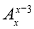= х Р_х-2.

Розв'язання

Використаємо формулу (3)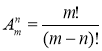 

х – (х – 3) = 3,  х >2, х N.

;

(х – 2)!(х – 1)х = 6х(х – 2)!;

(х – 2)!(х – 1)х – 6х(х – 2)! = 0;

(х – 2)!х(х – 1 – 6) = 0;

(х – 2)! ≠ 0, х ≠ 0, х – 7 = 0,

х = 7.

Відповідь. х = 7.

 

6. Розв'язати рівняння .

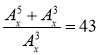Розв'язання

.

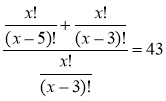Поділимо чисельник і знаменник одержаного дробу на х! (який не може дорівнювати 0) і домножимо на (x – 5)!, одержимо:

 

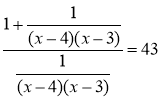
(х – 4)(х – 3) + 1 = 43;

х² - 7х + 13 = 43;

х² – 7х – 30 = 0;

х₁ = 10, х₂ = -3.

За умовою х ≥ 5, тому розв'язком рівняння є лише число 10.

Перевірка

= 10 ∙ 9 ∙ 8 ∙ 7 ∙ 6;   = 10 ∙ 9 ∙ 8;

 .

Відповідь. х = 10.

 

IV. Домашнє завдання.

1. Скільки різних чотирицифрових чисел можна утворити з цифр 0, 1, 2, 3, не повторюючи цифри у запису числа?
2. В одинадцятому класі 30 учнів. Вони обмінялись один із одним фотокартками. Скільки фотокарток було роздано?

Розв'язати рівняння: а) ;  б) = 42.

Задачі для домашнього завдання

 і відповіді до них.

 

1. Скоротити дріб:

       1)      Відповідь: 30              2)       Відповідь: 840

 

2. Скільки чотирицифрових чисел можна скласти з цифр: «2; 7; 8; 6»?

       Відповідь:  

 

3. Скількома способами можна вибрати два олівця різного кольору з дванадцяти різнокольорових олівців?

       Відповідь: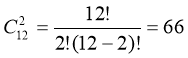    

 

4. Комісія складається з голови, заступника і ще п’яти осіб. Скількома способами сім членів комісії можуть розподілити між собою обов’язки голови і заступника?

       Відповідь: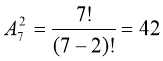

 

5. Мають набори з десяти різних букв і п’яти різних цифр.                                          

       Скількома способами можна обрати:

 

       1) одну букву або цифру? Відповідь: правило суми – 15

 

       2) набір з однієї букви і однієї цифри?

Відповідь: правило добутку – 50

 

6. Скільки трицифрових чисел з різними цифрами можна скласти з набору « 1; 2; 3; 4; 5»?

 

7. На площині позначено 8 точок (жодні 3 не лежать на одній прямий). Скільки існує трикутників з вершинами в цих точках?

 

8. Скількома способами можна розставити 7 книжок на полиці?

 

9. З 10 учнів потрібно вибрати двох для прибирання кабінету. Скільки існує варіантів вибору?

 

10. Розклад містить 4 пари на день з різних 10-ти предметів. Скільки існує варіантів скласти розклад на один день(предмети не повторюються)?

 

11. Скільки парних трицифрових чисел (усі цифри різні) можна записати, використовуючи цифри: «3; 4; 5; 7; 9»?

 

12. Скільки п’ятицифрових телефонних номерів існує з цифр «0; 1; 3; 5; 7», які в номері не повторюються?

 

13. У вазі стоїть 10 червоних і 5 рожевих пронумерованих гвоздик. Скількома способами можна вибрати:

 а) три квітки одного кольору?

 б) 3 червоні і 2 рожеві гвоздики?

 Відповідь:   а) Схема:  

 

 б) Схема: 

 

14. В кабінеті банкіра є сейф з коштовностями, код до якого складається  з двох голосних букв і трьох цифр. Скільки комбінацій треба перебрати грабіжнику, щоб відкрити сейф і заволодіти коштовностями?

 

15. Із двох математиків і десяти економістів треба створити комісію з восьми вчених, в яку обов’язково входить хоча б один математик?

 

16.  Скільки трицифрових чисел з різними цифрами можна скласти з набору « 1; 2; 3; 4; 5»?

Схема: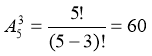   

17. На площині позначено 8 точок (жодні 3 не лежать на одній прямий). Скільки існує трикутників з вершинами в цих точках?

Схема: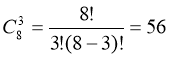   

18. Скількома способами можна розставити 7 книжок на полиці?

Схема:     

 

19. З 10 учнів потрібно вибрати двох для прибирання кабінету. Скільки існує варіантів вибору?

Схема: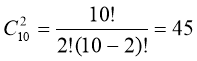        

20. Розклад містить 4 пари на день з різних 10-ти предметів. Скільки існує варіантів скласти розклад на один день(предмети не повторюються)?

Схема: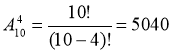      

21. Скільки п’ятицифрових телефонних номерів існує з цифр «0; 1; 3; 5; 7», які в номері не повторюються?

 

22. В кабінеті банкіра є сейф з коштовностями, код до якого складається  з двох голосних букв і трьох цифр. Скільки комбінацій треба перебрати грабіжнику, щоб відкрити сейф і заволодіти коштовностями?

 

Схема:        

 

23. Із двох математиків і десяти економістів треба створити комісію з восьми вчених, в яку обов’язково входить хоча б один математик?

 

Потрібен 1 математик з 2-х і 7 економістів з 10-ти:

Схема:         

                               Або

Потрібно 2 математика з 2-х і 6 економістів з 10-ти:

Схема:        

Правило суми:

 

Задача підвищеної складності

    Підприємство може  надати  роботу за однією спеціальністю чотирьом жінкам, за другою – шести чоловікам і за третьою – трьом робітникам незалежно від статі. Є 14 претендентів: 6 жінок і 8 чоловіків. Скількома способами можна заповнити вакантні місця?

                                      Розв’язок.

Маємо 13 робочих місць і 14 претендентів.

1 спеціальність – 4 жінки з 6-ти: Залишилося 2 жінки.

2 спеціальність – 6 чоловіків з 8-ми: Залишилося 2 чоловіки

3 спеціальність – 3 особи незалежно від статі:

             1) 1 жінка і 2 чоловіки:

                                       Або

            2) 1 чоловік і 2 жінки:

За правилом суми: 2 + 2 = 4 – варіанти для 3-ої спеціальності

За правилом добутку: 15∙28∙4=1680 – способів заповнити вакантні місця.

 

Самостійна робота за індивідуальними картками

 

КАРТКА № 1

1. Мають 5 видів фарби. Скількома способами можна розфарбувати слово «свято», якщо всі букви повинні бути різного кольору?

  2. Із цифр «1; 2; 3; 4; 5» складають числа, в яких не менше

 4-х різних цифр. Скільки таких чисел можна скласти?

Відповідь:   1.                     2.

 

КАРТКА № 2

1. Скількома способами можна розставити 7 спортсменів на 7-ми бігових доріжках?

2. В загоні 6 офіцерів і 15 рядових. Скількома способами можна сформувати загін розвідників, до якого входять 2 офіцера і 12 рядових?

Відповідь:   1.                2.

КАРТКА № 3

1. Скількома способами можна розкласти 8 різних поштових листів по восьми різним конвертам?

2. Мають 12 червоних і 7 білих пронумерованих троянд. Скількома способами можна скласти букет з 5-ти троянд одного кольору?

Відповідь:   1.              2.

 

КАРТКА № 4

1. Естафета має 4 різні за довжиною етапи. Скількома способами тренер може розподілити етапи серед 10-ти спортсменів?

2. У 6-ти дорослих та 11-ти дітей виявлено ознаки інфекційної хвороби. Щоб перевірити захворювання, треба взяти вибірковий аналіз у 2-ох дорослих та 3-х дітей. Скількома способами це можна зробити?

Відповідь:    1.              2.

 

КАРТКА № 5

1. Скільки існує варіантів розподілу 3-х призових місць, якщо в олімпіаді з математики беруть участь 25 студентів?

2. У кошику 10 яблук і 12 груш. Скількома способами можна дістати 6 фруктів одного виду?

Відповідь:      1.              2.

 

КАРТКА № 6

1. В побудовану нову школу прийшли працювати 25 викладачів. Скількома способами можна обрати з них директора, заступника з навчально-методичної роботи та заступника з виховної роботи?

2. В групі навчаються 15 хлопців і 12 дівчат. Скількома способами можна вибрати для генерального прибирання кабінету 3 хлопця і 4 дівчини?

Відповідь:      1.             2.

 

КАРТКА № 7

1.Скільки існує способів вибрати 4-х з 19-ти студентів, які бажають чергувати по технікуму?

2. В ювелірну майстерню привезли 6 ізумрудів і 9 алмазів. Ювеліру замовили браслет, в якому 3 ізумруди і 5 алмазів. Скількома способами він може вибрати камені на браслет?

Відповідь:     1.                2.

 

 КАРТКА № 8

1. Скількома способами можна вибрати три з 11-ти різних новорічних подарункових наборів?

2. При формуванні екіпажу космічного корабля мали 10 претендентів на посаду командира і 20 – на посаду бортінженера. Скількома способами можна обрати 2-х кандидатів однієї посади для проходження першого тесту?

Відповідь:  1.          2.

 

 

Самостійна робота.

1. Яка з множин С, D, F, Р, Q є

а) перерізом;  б) об'єднанням; в) різницею множин A і B, якщо

1-й варіант

А = {а, b, с, d, e}, В = {b, с, k}, С = {a, b, с, d, e, b, с, k}, D = {b, c},

F ={а, d, е}, Р = {а, b, с, d, е, k}, Q = {a, d, e, k}?

2-й варіант

А = {1, 2, 3, 4, 5}, В = {2, 4, 6}, С = {2, 4}, D = {1, 3, 5}, F = {6},

Р = {1, 2, 3, 4, 5, 6}, Q = {1, 2, 3, 4, 5, 2, 4, 6}?

Чи є різниця множин А і В доповненням множини В відносно множини A?

2. Спростити вираз.

1-й варіант .   2-й варіант .

 

3. Розв'язати рівняння.

1-й варіант .  2-й варіант .

 

Розв'язання завдань самостійної робота

1-й варіант

1. А 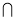В = D, А 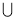В = Р, А \ В = Е. Різниця множин А і В не є доповненням множини В відносно множини А.
2. .
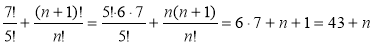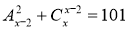3. , х ≥ 2, х 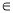N.

,

,

,

2x² – 10x + 12 + x² – x – 202 = 0,

3х² – 11х – 190 = 0,

х₁ = 10, х₂ =   - не належить області допустимих значень рівняння. Відповідь. х = 10.

 

2-й варіант

1. А 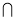В = C, А 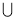В = Р, А \ В = D. Різниця множин A і В не є доповненням множини В відносно множини А.
2. .
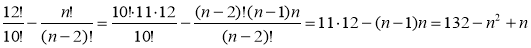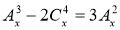3. , х ≥ 4, х 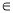N.

,

,

х(х – 1)(12(х – 2) – (х – 3)(х – 2) – 36) = 0,

х ≠ 0, х ≠ 1, отже, 12х – 24 – х² + 5х – 6 – 36 = 0,

- х² + 17х – 66 = 0,  

х² – 17х + 66 = 0,

х₁ = 6, х₂ = 11.

Виконавши перевірку, переконуємося, що обидва корені є розв'язками даного рівняння.

Відповідь. х₁ = 6, х₂ = 11.

 

 

 

Задача 1. Записати всі підмножини множини {1, 3}; {1, 3, 5}. Скільки їх? Чи можна записати це число через степінь одного і того самого числа?

Відповідь. 4 = 2², 8 = 2³.

Задача 2. Використовуючи формулу 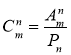, властивості кількості комбінацій з т елементів по n елементів та співвідношення = = = 1, скласти таблицю чисел .

Числа т	Числа п								2n
	0	1	2	3	4	5	6			, , , , ,
0	1							1	2°
1	1	1						2	21
2	1	2	1					4	22
3	1	3	3	1				8	23
4	1	4	6	4	1			16	24
5	1	5	10	10	5	1		32	25
6	1	6	15	20	15	6	1	64	26

Ця таблиця дістала назву трикутника Паскаля.

Розглянемо закономірності утворення таблиці.

1. Числа в таблиці — кількість комбінацій з т елементів по n елементів; числа лівого стовпчика — кількість елементів множини; числа верхнього рядка кількість елементів підмножини (сполуки).
2. Кожний рядок починається закінчується 1.
3. Сума чисел кожного рядка дорівнює 2т, т = 0, 1,2,3,...
4. Кожне число наступного рядка дорівнює сумі двох чисел попереднього рядка, що стоять над ним.

Наприклад, у 5-му рядку: 5 = 1 + 4, 10 = 4 + 6; у 6-му рядку: 6 = 1 + 5, 15 = 5 + 10, 20 = 10 + 10, ...

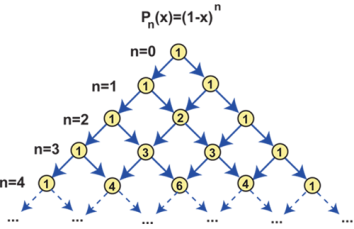5. Числа, розміщені на однаковій відстані від кінців рядка, рівні між собою 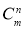= 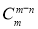(за властивістю 1).

Учні самостійно заповнюють рядок чисел, якщо т = 7. Інша форма запису трикутника Паскаля:

 

Означення. Двочлен а + b називається біномом.

Запишемо послідовно у вигляді многочлена степені бінома з нульовим і натуральним показниками:

(а + b)⁰= 1,

(а + b)¹= 1∙а + 1∙b,

(а + b)² = 1∙а² + 2∙аb + 1∙b²,

(а + b)³ = 1∙а³ + 3∙а²b + 3∙аb² + 1∙b,

(а + b)⁴ =((а + b)²)² =(а² + 2аb + b²)² = 1∙а⁴ + 4а³b + 6∙а²b² + 4∙аb³ + 1∙b⁴.

Бачимо, що коефіцієнти розкладу степеня бінома дорівнюють числам трикутника Паскаля.

Теорема. Коефіцієнти розкладу (а + b)ⁿ збігаються з п-м рядком трикутника Паскаля, тобто для будь-якого натурального показника п виконується рівність:

(а + b)ⁿ = аⁿ + a^n-1b + а^n-2b²+ ...+ a^n-mb^т+...+ bⁿ.

Ця формула дістала назву бінома Ньютона на честь видатного англійського математика і фізика Ісаака Ньютона.

Коефіцієнти правої частини називаються біноміальними коефіцієнтами.

Приклад 1.

(1 + х)⁷ = 1 + 7х + 21х² + 35х³ + 35х⁴ + 21х⁵ + 7х⁶ + х⁷.

Приклад 2.

(1 – х)⁷ = 1 – 7х + 21х² – 35х³ + 35х⁴ – 21х³ + 7х⁶ – х⁷.

Знаки многочлена чергуються, бо можна вважати, що а = 1, b = - х.

Формула загального члена розкладу степеня бінома:

Приклад 3. Записати восьмий член розкладу (x – у)¹².

Розв'язання

(х – у)¹²=(х + (-у))¹².

Т₈ = T₇₊₁ = а⁵b⁷ , а = х, b = -у.

= = = 72 ∙ 11 = 792.

T₈ = -792 х⁵y⁷.

Відповідь. -792 х⁵y⁷.

Домашнє завдання.

1. Записати восьмий і дев'ятий рядки трикутника Паскаля.
2. Записати розклад степеня бінома: а) (х² + 2х³)⁴; б) .
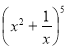3. Розв'язати рівняння .

 

 

 

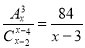Комбінаторні задачі на інших уроках:

Урок фізичної культури

1.   На збори прийшло 12 баскетболістів. Скільки може бути утворено тренером різних стартових «п’ятірок»?  
2.  Для участі в змаганнях з баскетболу необхідно скласти команду за умови: 3 члена команди – з числа 25 спортсменів м. Ізмаїла, 2  - з числа 20 гравців м. Одеси та запасний гравець – з числа 8 спортсменів м. Іллічівськ. Скількома способами можна скласти команду?  
3.   Якщо тренуються в клубі 33 футболісти, то скількома способами можна обрати дише 11 з них для гри з суперниками?  

Урок української мови та літератури

4. В українській літературі є дуже цікавий твір «Тигролови». Скільки слів можна отримати, переставляючи букви в цьому слові? 

 

5.  Незнайці дали завдання: скласти зі слова «охайний» всі можливі слова. Скільки слів він отримав? Яка ймовірність, що з набору даних букв можна зробити слово «охайний»?
6.  «Одного разу трапилась така повінь, якої не пам’ятала навіть столітня прабабка. У батька був один човен на всю округу, тому до нього прийшов Макар і велів їхати рятувати людей на греблі. Човен вміщав 4 людини. Цікаво, скільки способів існує для розміщення 17 людей, яких потрібно рятувати, на чотиримісному човні? (О. Довженко «Зачарована Десна»).
7.   Іван Франко – автор збірки оповідань «В полі чола», «З вершин і низин», «Зів’яле листя», «Мій Ізмарагд»,  «Із днів журби», «Гімн», «Декадент», має обрати два оповідання для друку в журналі «Житє і слово». Скількома способами він може це зробити? 
8.   Відомо, що у збірку творів Т.Г. Шевченка «Кобзар»  1840 року входять такі твори: «Гайдамаки», «Гамалія»,  «Тарасова ніч», «Іван Підкова», «Катерина», «Наймичка», «Лілея», «Мар’яна – чорниця», «Сон». Скількома способами можна обрати 3 твори для читання на весняних канікулах?  
9.   Микола Хвильовий складав вірші. Для рими йому подобались 4 слова (з 25 слів) та 5 фразеологізмів (з 10 штук). Скільки різних віршів він міг скласти?
10.                  Скількома способами 5 героїв п’єси «Мина Мазайло» можуть розміститися на 5-місному ослоні? 

Урок зарубіжної літератури

11.  Біля вогнища сиділо 12 місяців та думали – гадали, як їм відповідати за 4 пори року, якщо в кожній має бути по 3 місяця. Скількома способами можна обрати 1-у групу?, 2-у групу?, 3-у групу?, 4-у групу?. Та скількома способами серед утворених груп розподілити пори року?  

12.  У казці про Білосніжку та 7 гномів не все було розказано…. Одного дня трьом з них потрібно було прибрати домівку, двом – спекти пиріг та зготувати обід, ще двом – назбирати ягід в лісі. Скількома способами може Білосніжка розподілити обов’язки на день серед 7 гномів?  

 13.  На полиці є 6 книг: 5 підручників та 1 – про цирк. Скількома способами можна обрати 3 книги, якщо а) книга про цирк обов’язково потрібна; б) книга про цирк – не обов’язкова?  

Урок художньої культури

14. Цвєтік – семицвєтік має 7 різнокольорових пелюсток. Якщо його нафарбувати, то скільки варіантів можна отримати?  

15.  Треба зробити аплікацію з 8 кольорових кульок (маємо 7 зелених та 4 жовтих), але так, щоб було не менша 2-х жовтих.  (

16.  Художнику запропонували подати на виставку 6 картин, а в нього всього 15 готових робіт. Скількома способами він обере саме 6 необхідних для виставки  з 15-ти власних робіт?

Урок біології

17.  Для дитини потрібні вітаміни! Маючи 2 яблука та 3 груші, дитина кожен день мусить з’їсти один фрукт. Скількома способами це можна зробити? Яка ймовірність того, що в останній день вона з’їсть яблуко?  

18.  У дівчинки було 60 букетів квіт. Але всього 5 кошиків, а в один кошик можна було покласти лише 5 букетів. Скількома способами вона може зробити, якщо всі букети різні?  

19.  Потрібно сформувати клумбу з 7 видів квіт, але так, щоби на ній було не менше 3 ромашок. Скільки способів існує, якщо маємо 6 видів ромашок та 13 видів троянд? 

Урок історії

20. У одного з Богів Олімпу було 60 доньок, а у іншого – 60 синів. Скількома способами їх можна одружити, зацікавились Боги та призвали до відповіді математиків.

Урок географії

21. Компанії «3 мушкетера та Д’Артаньян» потрібно потрапити з Парижу до Ліону. Для таємного пересування вони обрали карету. Скількома способами можуть розміститися друзі, якщо в салоні 4 місця, ще й біля візника 2 місця, та за домовленістю лише Д’Артаньян керує кіньми? 

22.  На компанію «3 мушкетери та Д’Артаньян» є лише 3 коня, проте кожен кінь може витримати двох чоловік. Скількома способами вони можуть розміститися на конях? 

 23. «Лебідь, щука та рак»: коли лебідь та щука захворіли, ракові потрібно було сходити в ліс за грибами, на річку за водою, назбирати трав для цілющого чаю. Скількома маршрутами він може це зробити? 

Урок математики

24.  Скільки різних трицифрових чисел можна написати цифрами 6,7, і 8 так, щоб усі цифри кожного числа були різні?

25.  Дано цифри: 0, 1, 2, 3, 4. Знайти кількість п’ятизначних круглих чисел. Яка ймовірність того, що на прохання вчителя навести приклад, учень відповість: 12340?

Урок музичного мистецтва

26. За казкою «Бременські музики» головний герой закохався в принцесу. Уявіть, що її треба викрасти, але це можуть зробити лише двоє з чотирьох його друзів. Яка ймовірність того, що це зроблять разом Осел та Півень?  

Урок інформатики

27. Для того, щоби зібрати системний блок, потрібно мати відео карту,  жорсткий диск, дисковод, кулер, материнську плату.  У магазині запропонували вибрати з: 11 відеокарт, 14 жорстких дисків, 6 дисководів, 17 кулерів, 8 материнських плат. Скількома способами можна зібрати системний блок? 

 

 

 

 

1-й варіант

І рівень (3 бали)

Дано множини А = {т, п, р, 11,12,13} і В = {т, п, р, х}. Знайти їх:

а) переріз;

б) об'єднання;

в) різницю А\В;

г) різницю В\А.

Чи є різниця А\В доповненням множини В відносно множини А?

 

II рівень (3 бали — по одному за кожне завдання)

1. Обчислити: 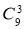+Р₃.
2. Спростити вираз: .
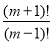3. На площині розміщено я точок, жодні три з яких не лежать на одній прямій. Скільки різних пря­мих можна провести через ці точки?

 

III рівень (2 бали за перше завдання + 1 бал за друге)

1. Розв'язати рівняння .
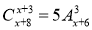2. Записати розклад бінома (2х – у)⁵.

 

IV рівень (3 бали)

У розкладі бінома 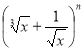п'ятий член розкладу не залежить від х. Знайти п.

2-й варіант

І рівень (3 бали)

Дано множини А = {а, b, с, 101, 102, 103} і В = {101, 102, 103, 104}. Знайти їх:

а) переріз;

б) об'єднання;

в) різницю А\В;

г) різницю В\А.

Чи є різниця А\В доповненням множини В відносно множини А?

 

II рівень (3 бали — по 1 балу за кожне завдання)

1. Обчислити: 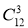+Р₄.
2. Спростити вираз: .
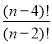3. Скільки можна утворити різних п'ятицифрових чисел із п'яти цифр 1, 2, 4, 5, 0, не повторюючи їх?

 

ІII рівень (2 + 1 бали)

1. Розв'язати рівняння .
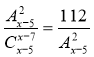2. Записати розклад бінома (2у – х)⁴.

 

IV рівень (3 бали)

У розкладі бінома 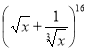визначити член розкладу, який містить х³.

 

Розв'язання завдань

1-й варіант

І рівень

а) С = АВ, С={т, п, р};

б) D = АВ, D = {т, п, р, х, 11, 12, 13};

в) А\B = {11, 12, 13};

г) B\A = {x}.

Різниця множин А і В не є доповненням множини В відносно множини А.

 

II рівень

1. .

2. .

Відповідь. т² + т.

3. Оскільки пара точок не є впорядкованою, то кожна підмножина, утворена з двох точок, через які проведено пряму, є комбінацією з п елементів по 2:  .

Відповідь. (n² – n) різних прямих.

 

III рівень

 , х ≥ -3, х N.

,

(х + 4)(х + 5)(х + 6)(х + 7)(х + 8) – 5! ∙ 5 ∙ (х + 6)(х + 5)(x + 4) = 0,

(х + 6)(х + 5)(x + 4)(х² + 15x + 56 – 600) = 0,  

х₁ = - 6, x₂ = - 5, x₃ = - 4,  х² + 15x – 544 = 0,

D = 2401 = 49², х₄ = 17, x₅ = -32.

Із одержаних коренів лише x = 17 задовольняє умову.

Відповідь. х = 17.

 

IV рівень

У розкладі бінома 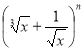п'ятий член 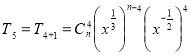не залежить від х.

, , , n = 10.

Відповідь, n = 10.

 

2-й варіант

I рівень

а) С = АВ, С = {101, 102, 103};

б) D = АВ, D = {а, b, с, 101, 102, 103, 104};

в) А\В = {а, b, с};

г) В\А = {104}.

Різниця множин А і В не є доповненням множини В відносно множини А.

 

II рівень

1. .

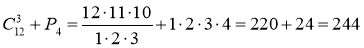Відповідь. 244.

2. .

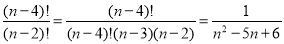Відповідь. .

3. Різних п'ятицифрових чисел із п'яти цифр можна утворити Р₅, з них мають 0 на початку Р₄ чисел. Отже, всього різних п'ятицифрових чисел можна утворити

Р₅ – Р₄ = 5! – 4! = 120 – 24 = 96.

Відповідь. 96.

III рівень

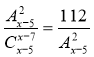, x ≥ 7, x   N.

.

; .

,

х² – х = 56,

x₁ = 8, х₂ = -7; -7 ОДЗ.

Відповідь, х = 8.

 

IV рівень

Розглянемо біном 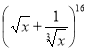, який можна записати у вигляді .

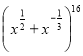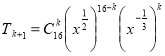, , , , k = 6.

Відповідь. Множник x³ є у сьомого члена розкладу.

 

 

 

№1

    У чайному кіоску в наявності є лише розфасований у коробки по 100г листовий чорний чай 7 видів, серед яких є вид «чорна перлина». Покупець вирішив придбати в цьому кіоску для подарункового набору три коробки чорного чаю трьох різних видів, серед яких обов’язково повинен бути вид «чорна перлина». Скільки всього в покупця є варіантів такого придбання трьох коробок чаю для набору з наявних у кіоску?

 

№2

    Марійка зірвала на клумбі 9 нарцисів та 4 тюльпани. Скільки всього існує способів вибору із цих квітів 3 нарцисів та 2 тюльпанів для букета?

 

Розв’язання:

№3

 У школі є два 11-х класи. В 11-А класі навчається 12 хлопців та 8 дівчат, а в 11-Б – 9 хлопців та 15 дівчат. З учнів цих двох класів потрібно обрати двох відучих для проведення святкового вечора, причому хлопець має бути з 11-А класу, а дівчина з 11-Б класу. Скільки існує всього варіантів вибору таких пар ведучих?

№4