Відкрите заняття з дисципліни "Креслення" на тему: "Проектування геометричних тіл"".

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ВІННИЦЬКИЙ КОЛЕДЖ
НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ ХАРЧОВИХ ТЕХНОЛОГІЙ

 

 

 

 

 

 

 

 

 

ПЛАН –  КОНСПЕКТ

відкритого заняття

з дисципліни „Креслення”

 

тема :”Проектування геометричних тіл”

 

 

 

 

 

 

 

 

 

 

 

ВИКЛАДАЧ  ЯНЧУК Н.А.

 

 

 

 

 

 

ВІННИЦЯ , 20015

ПЛАН ЗАНЯТТЯ

 

Дисципліна : Креслення

Група: 2АМ2

Викладач:   Янчук Н.А.

Вид заняття: лекція

Мета заняття :

1. Навчальна: вивчити методи проектування геометричних тіл
2. Виховна:  виховання пізнавального інтересу до предмету, активності , самостійності міркувань.
3. Розвиваюча:  розвиток просторового та логічного мислення.

 

Між предметні зв’язки:   математика „Багатогранники та їх поверхні”

Методичне та матеріальне забезпечення: 

1. Моделі геометричних тіл
2. Плакати для магнітної дошки „Проектування геометричних тіл”
3. Індивідуальні картки-завдання.

Література:

1. Хаскин А.М. Креслення  К.: Вища школа , 1985 с,127-146
2. Боголюбов С.К. Черчение  М.: Машиностроение , 1989 с.89-96

 

Методична спрямованість заняття :  Використання проблемних методів навчання, як засобу активізації пізнавальної діяльності студентів.

 

ХІД ЗАНЯТТЯ

1.              Організаційний момент                                                                   2 хв.
   1.                    Привітання.
   2.                     Перевірка присутності студентів на занятті.

 

2. Перевірка домашнього завдання   та актуалізація опорних знань студентів.                                                                                                                    10 хв.              

      Шляхом  тестового опитування по темі „Методи проектування”.                     Перевірка відповідей відкритим кодом.

      Актуалізація опорних знань студентів  проводиться в процесі вивчення нового матеріалу  шляхом співбесіди. Студенти пригадують відповідні поняття, відповідають  на питання викладача.

 

3.Мотивація навчальної діяльності студентів.                                       5хв.

Проводиться з використанням перспективно-спонукальних мотивів які ґрунтуються на розумінні прикладного значення предмета.

        Вивчення цієї теми дозволяє засвоїти методи, які використовують при побудові креслень та вивчити поверхні геометричних тіл, які утворюють технічні форми ( аналіз елементів багатогранника).

        Щоб накреслити складну  технічну деталь , потрібно навчитися будувати проекції простих геометричних тіл  з яких складаються деталі – призм, циліндрів, конусів , куль тощо.

 

4.Вивчення і засвоєння  нового матеріалу.                                55 хв.

      4.1. Тема заняття: Проектування геометричних тіл.

 

   4.2. Питання які будуть вивчатися на занятті:

 

1.             Проектування призми.
2.             Проектування піраміди.

 

   4.3. Методи, які використовуються: Вивчення і засвоєння нового матеріалу  проходить методом бесіди з елементами проблемного навчання.

 Студенти пригадуючи відповідні поняття, відповідають на питання викладача, викладач уточнює і доповнює відповіді студентів.

 

1. ПРОЕКТУВАННЯ ПРИЗМИ.

 

Якщо твірна ковзає по довільній напрямній замкненій ламаній лінії так, що окремі її положення залишаються між собою паралель­ними, то утворюється призматична поверхня.

Дві грані призми (основи) є однаковими многокутниками з від­
повідно паралельними сторонами, а бічні грані в загальному випад­
ку — паралелограмами (рис.1,а). Лінії перетину граней назива­
ються ребрами. Ребра призми поділяють на бічні і ребра основи. Точ­
ки перетину ребер, або точки, в яких сходяться грані, називаються
вершинами многогранника. 

Призма називається прямою (рис. 1.б), коли бічні ребра перпендикулярні до основи, і похилою (рис.1,б), коли вони не перпендикулярні. Бічні грані прямої призми — прямокутники, по­хилої — паралелограми. Призми поділяються на правильні і непра­вильні. Правильною називається призма, в основі якої лежить пра­вильний многокутник. За формою основи призми бувають трикутні, чотирикутні, шестикутні і т. д. Коли в основі призми лежить прямо­кутник або паралелограм, вона називається паралелепіпедом. Пря­мий паралелепіпед, в основі якого лежить прямокутник, називається прямокутним (рис.1,в).

Побудова проекцій призми на комплексному кресленні (рис.2, а). Треба побудувати проекції прямої правильної трикутної призми, що стоїть на площині П₁. Основа вписана в коло . На площину проекцій П₁ призма проектується рівностороннім трикутником, який є проекцією нижньої і верхньої основ призми. Сторони трикутника є проекціями бічних граней призми, а його вершини — проекціями бічних ребер. На площині проекцій П₂ призма зобразиться у вигляді прямокутника, величина якого до­рівнює грані, паралельній площині П₂. Проекція переднього ребра призми ділить прямокутник навпіл. На площину П₃ призма проекту­ється у вигляді прямокутника, величина якого буде меншою за нату­ральну величину бічної грані призми. На рис. 2,а побудову про­фільної проекції виконано за допомогою постійної прямої креслення.

Видимість елементів призми. Горизонтальна проекція — це зоб­раження призми в напрямі стрілки  (рис2, в). Тому на площині П₁ видимою буде лише верхня основа призми. Стрілка ІІ показує напрям променів зору при побудові фронтальної проекції; отже на ти проекції грані AEFB і FDCB видимі, а грань AEDC — невидима. На профільній площині видимою буде лише бічна грань AEFB, бо напрям зору відповідає стрілці ІІІ .

 

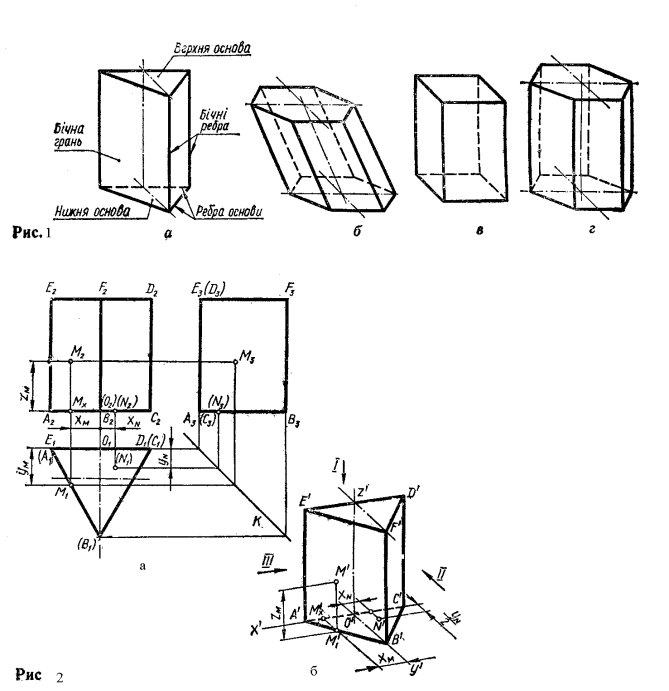
Визначення проекцій точок, що лежать на  поверхні призми.  На

рис. 2, а задано фронтальну проекцію М₂ точки, яка лежить на лі­вій бічній грані призми. Ця грань перпендикулярна до площини П₁ і проектується на неї відрізком А₁В₁. Отже, горизонтальна проек­ція M₁ точки лежить на цьому відрізку. Проекцію М₃ знайдено за допомогою постійної прямої креслення. На цьому самому рисунку побудовано фронтальну і профільну проекції невидимої точки N, яка лежить на нижній основі призми. Побудова зрозуміла з креслення.

Побудова аксонометричного зображення призми. На рис.2, в призма зображена в прямокутній диметрії. Послідовність побудови показано на рис3, а—в. Проводять аксонометричні осі х', у', z' і будують зображення нижньої основи призми (рис.3 а). Відкла­дають по осі х' відрізки О'А' і О'С', що дорівнюють відповідно 01А₁ і C1О1, і дістають вершини А' і С' трикутника (рис3,а). По осі у' відкладають половину висоти трикутника основ

 Сполучаючи точки А', В', С', дістають зображення ниж­ньої основи призми. З вершин основи проводять прямі, паралельні осі z' (рис. 3,б), і відкладають на них відрізки, що дорівнюють дов­жині бічних ребер призми. Сполучаючи кінцеві точки цих відрізків, мають зображення верхньої основи приз­ми (рис. 3, в). Невидимі ребра наводять штриховою лінією. Пере­носять на аксонометричне зображення точки М і N. Роблять це спосо­бом координат.

 

 

 

 

 

 

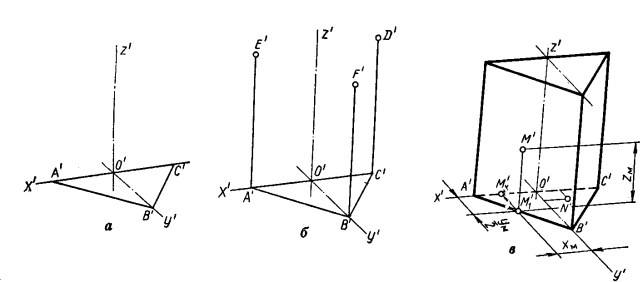
рис.3

 

2. ПРОЕКТУВАННЯ ПІРАМІДИ.

Якщо твірна лінія, що проходить через сталу точку, ковзає по замкненій ламаній лінії, то утворюється многогранний кут, або пі­рамідальна поверхня. Перерізаючи пірамідальну поверхню площиною, дістають піраміду

.

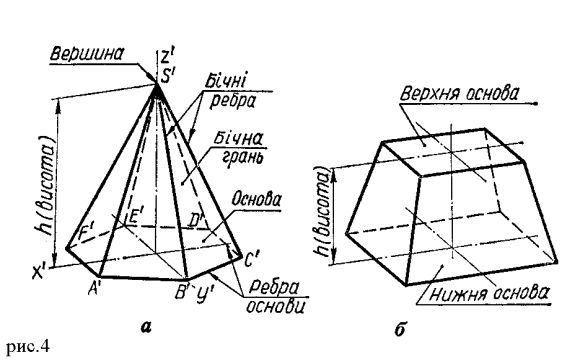
Отже,   пірамідою   називається  многогранник   (рис.   4, а), одна грань  якого (основа) є многокутник, а бічні грані — трикут­ники, що мають спільну точку — вершину піраміди. Лінії перетину граней називаються ребрами. Ребра піраміди по­діляють на бічні і ребра основи.

За формою основи піраміди бувають трикутні, чотирикутні, п'яти­кутні і т. д. Піраміда називається правильною, коли в її основі лежить правильний многокутник і вісь проходить через центр основи. Бічні грані правильної піраміди — рівнобедрені трикутники.

Найкоротша відстань від вершини до основи називається висотою піраміди. Якщо піраміду розсікти площиною, паралельною ЇЇ основі, то утвориться така частина піраміди, яка між основою і січною пло­щиною називається зрізаною пірамідою (рис. 4, б). Сторони верх­ньої і нижньої основ зрізаної піраміди паралельні між собою. Зріза­на піраміда називається правильною, коли в її основах лежать пра­вильні многокутники.

Побудова проекцій піраміди на комплексному кресленні. Треба побудувати проекції піраміди, в основі якої лежить чотирикутник  (рис 5, а). Горизонтальна проекція піраміди є чотирикутником, поділеним діагоналями на три­кутники. За формою і розмірами цей чотирикутник дорівнює основі піраміди. Трикутники є проекціями бічних граней піраміди. На пло­щині проекцій П₂ піраміда зображується трикутником . Трикутник є проекцією передніх  видимих граней піраміди. На площині П₃ піраміда зображується також трикутником.

Аналіз креслення піраміди. Піраміда, зображена на рис. 5, а, має 5 граней, 8 ребер, вершину S і чотири вершини прямокутника основи. Бічні грані піраміди є площнами загального положення і зображуються    площинах П_1, П₃ і П₂ — трикутниками зменшеної величини.  Основа піраміди ABCD лежить у площині П₁ і про­ектується на неї в натуральну величину.  Бічні ребра піраміди — прямі загального положення, які на жодну з площин проекцій не проектуються в натуральну величину. Ребра основи – горизонтальні прямі рівня і на площину П₁  проектуються в дійсну величину.

Видимість елементів піраміди. На горизонтальній проекції ви­димими будуть усі чотири бічні грані, на площині П₂ і  П₃ — дві бічних  грані. Визначення   проекцій точок, що лежать на поверхні  піраміди.

        На рис, 5, а задано фронтальну проекцію F2 точки, яка лежить на ребрі AS. Виходячи з умови, що точка лежить на прямій, коли її проекції лежать на однойменних проекціях цієї прямої, проводять вертикальну і горизонтальну лінії зв'язку і знаходять горизонтальну F₂ і профільну F₃ проекції.

Задана також фронтальна проекція  К₂  точки К. Побудова проекцій показана на рис.5. Через задану фронтальну проекцію  К₂  точки К проводять допоміжну пряму, яка проходить через вершину піраміди і розташована на її грані. Горизонтальну проекцію допоміжної прямої знаходять використовуючи лінії зв’язку. Горизонтальна проекція В₁  точки В знаходить на перетині  лінії  зв’язку, що  проведена через точку  В₂    з горизонтальною проекцією  допоміжної прямої.

     Побудова аксонометричного зображення. На рис. 5, б пірамі­ду побудовано в прямокутній діметрії. Проводять аксонометричні осі х', у', г'. Побудову починають з основи піраміди . Відкладають по осі х^/ довжину діагоналі АС,  а по осі у^/ - половину довжини діагоналі ВД. З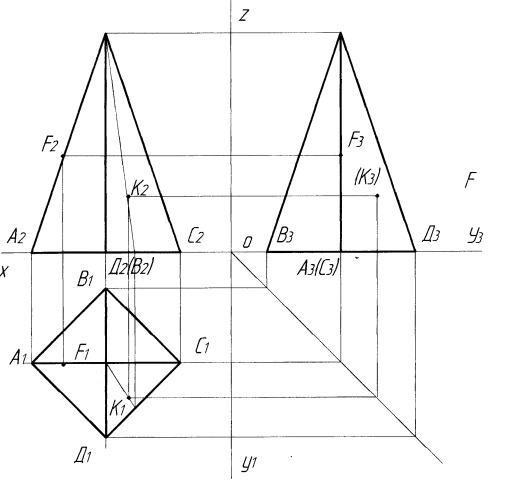

Рис. 5,а

точки О перетину діагоналей проводять вісь z^/  і на ній відкладають висоту піраміди. Вершину S сполучають з вершинами основи прямими лініями – ребрами.

       Фронтальну діметричну проекцію точки  К, що розташова на грані піраміди, будують  за координатами , які беруть на комплексному кресленні. Від початку координат О по осі х  відкладають координату  х_А , з її кінця паралельно осі у  - половину координати  у_А  і з кінця цієї координати паралельно осі z  - третю координату  z_{А ..} Побудова точки  F, що розташована на ребрі піраміди, простіше.  Від точки О відкладають координату х_F  і з її кін ця проводять пряму, паралельну осі  z  до перетину з ребром в точці F.

 

 

 

 

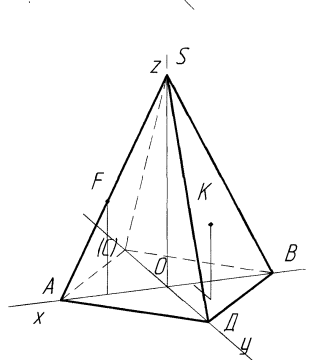
рис. 5,б

 

 Закріплення  проводиться шляхом виконання комплексних креслень геометричних тіл з  точками на їх поверхні.

 

5. Узагальнення та систематизація  вивченого матеріалу.                    3 хв.

 

6. Підсумкова   частина заняття.                                                                 3 хв.

 

7. Повідомлення домашнього завдання.                                                   2 хв.

1.Хаскин А.М. Креслення.  К.: Вища школа , 1985 с,127-146

2. Боголюбов С.К. Черчение  М.: Машиностроение , 1989 с.89-96

3. Підготувати формат А3 для виконання графічної роботи.