Відкритий урок + Презентація

Про матеріал

Розробка відкритого уроку з алгебри для 9 класу по темі лінійні нерівності.

Зміст архіву

з алгебри 9-А клас.docx docx
проект уроку.pptx pptx

Перегляд файлу

Тема уроку: Розв’язування лінійних нерівностей з однією змінною

Мета: відтворити знання про лінійні нерівності з однією змінною; удосконалювати вміння учнів розв’язувати нерівності з однією змінною; формувати навички самостійної роботи; розвивати увагу, пам’ять, мислення, культуру математичного мовлення; виховувати самостійність, активність, дисциплінованість, інтерес до математики.

Тип уроку: формування вмінь та навичок.

Обладнання: інтерактивна дошка, проектор, роздатковий матеріал: піктограми настрою, картки контролю знань, картки лото, мультимедійна презентація

Хід уроку

І. ФОРМУВАННЯ ТЕМИ, ВИЗНАЧЕННЯ МЕТИ, ЗАВДАННЯ УРОКУ

Досягти успіху можна тільки тоді, коли перед вами стоїть мета. Тому давайте сформулюємо мету уроку. Сьогодні ми:

повторимо відомості про лінійні нерівності з однією змінною;
удосконалимо вміння розв’язувати нерівності з однією змінною;
розвиватимемо увагу, пам'ять, мислення, культуру математичного мовлення

Під час уроку я стежитиму за вашим емоційним станом. Для цього ви маєте спеціальні «піктограми настрою»:

- гарний настрій;

- середній настрій;

- поганий настрій.

Покажіть, який у вас зараз настрій. Сподіваюсь, що наприкінці уроку ваш емоційний стан тільки покращиться.

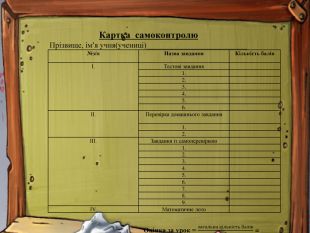
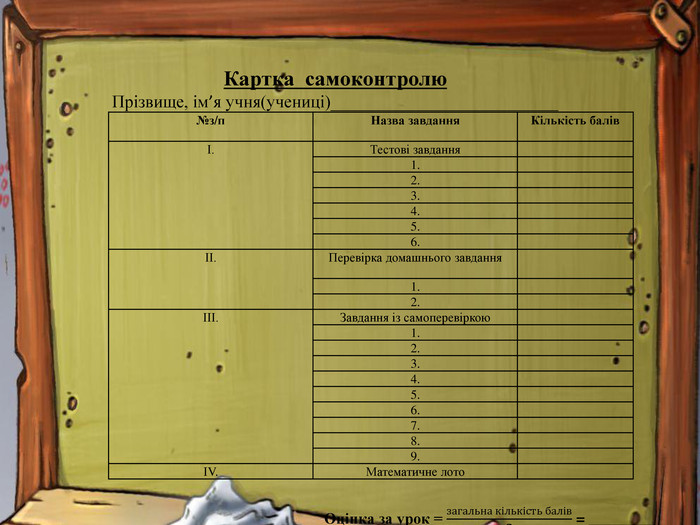
У вас на партах лежать картки самоконтролю, у яких ви виставлятимете одержані бали за кожен вид роботи.

Побажаємо один одному успіху і пам’ятаємо, що мудрим ніхто не народився, а навчився.

ІІ. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ. ДІАГНОСТИКА ВИКОНАННЯ ДОМАШНЬОГО ЗАВДАННЯ

Виконання тестових завдань з усним обговоренням

На екрані почергово демонструються тестові завдання, на які учні дають відповіді (за кожну правильну відповідь учень ставить собі в картку 0,5 бали).

Перевірка правильності розв’язання кожного завдання передбачає його обґрунтування та формулювання відповідних теоретичних відомостей.

1.Установіть відповідність між висловленням (1-4) та наслідком із нього (А-Г)

1	a > b	А	a – b = 0
2	a ≥ b	Б	a – b > 0
3	a = b	В	a – b ≤ 0
4	a ≤ b	Г	a – b ≥ 0

Правильна відповідь: 1-Б, 2-Г, 3-А,4-В

Запитання до учнів

Що таке нерівність?
Що таке числова нерівність?
У якому випадку число а вважається більшим від числа b?
У якому випадку число а вважається меншим від числа b?
У якому випадку число а вважається рівним числу b?

2. Відомо, що a > b. Які з поданих нерівностей є правильними?

А	Б	В
3a > 3b	a – 70 > b - 70	a – 5 > b – 10
Г	Д	Е
-6a < -6b	>	a – 6 < b - 6

Правильна відповідь: А, Б, Г, Д

3. Серед наведених нерівностей укажіть лінійну нерівність з однією змінною.

А	Б	В
2 < ≤ 6	- 4 < 9	х² – 5 > 0
Г	Д
х – 5 ≤ х + 6	х + у > 8

Правильна відповідь: А, Г.

Запитання до учнів

Яку нерівність називають лінійною нерівністю з однією змінною?
Що називають розв’язком нерівності з однією змінною?
Що означає розв’язати нерівність?

4. Які з поданих чисел є розв’язками нерівності 3х + 1 > 2 ?

А	Б	В	Г	Д
-2	-	0	0,5	4

Правильна відповідь: Г, Д.

5. Які з поданих нерівностей рівносильні?

А	Б	В
*5х+1>0 і 5х>1*	*3х<0 і х<0*	*-2х>0 і х>0*

Правильна відповідь: «Б».

Запитання до учнів

Які нерівності називаються рівносильними?
Які властивості нерівностей зі змінними ви знаєте?
Скільки розв’язків може мати лінійна нерівність з однією змінною?

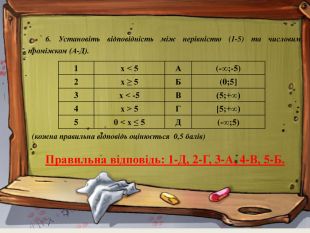
6. Установіть відповідність між нерівністю (1-5) та числовим проміжком (А-Д).

1	*х < 5*	А	*(-∞;-5)*
2	*х ≥ 5*	Б	*(0;5*]
3	*х < -5*	В	*(5;+∞)*
4	*х > 5*	Г	*[5;+∞)*
5	*0 < х ≤ 5*	Д	*(-∞;5)*

Правильна відповідь: 1-Д, 2-Г, 3-А, 4-В, 5-Б.

Перевірка домашнього завдання

№ 5.7 (ст.36)

Відповідь: 3) (-∞;8,99]

№ 5.20 (ст.37)

Відповідь: 1. (-∞;-3);

2. (-∞;10];

3. (4;+∞);

4. [5,5;+∞).

(правильність № 5.7 – 1 бал; № 5.20 – 2 бали)

Двоє учнів на дошці розв’язують вправи, аналогічні до домашнього завдання. Відбувається перевірка за правильними відповідями, що розміщені на екрані. Учні обговорюють розв’язання (за правильно розв’язані завдання учні в картки самоконтролю виставляють 1,5 бали).

Картка1

Запишіть усі цілі числа, що належать проміжку (-1,2;4].
Розв’яжіть нерівність 3х+1 ≥ 4х-6.

Картка 2

Запишіть усі цілі числа, що належать проміжку [-2;3,5).
Розв’яжіть нерівність 5х+8 ≤ 2-3х.

ІІІ. УДОСКОНАЛЕННЯ ЗНАНЬ

Виконання тестових завдань з самоперевіркою

За кожне правильно виконане завдання учні виставляють у картки самоконтролю 1 бал

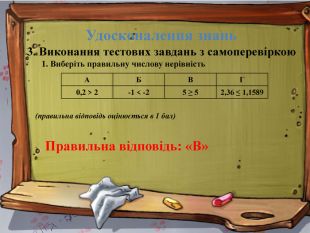
1. Виберіть правильну числову нерівність

А	Б	В	Г
0,2 > 2	-1 < -2	5 ≥ 5	2,36 ≤ 1,1589

Правильна відповідь: «В»

2. Сумою нерівностей 5 > 3 і 2 > -1 є нерівність

А	Б	В	Г
4 > 5	4 < 5	7 > 2	7 ≥ 2

Правильна відповідь: «В»

3. Укажіть строгу нерівність

А	Б	В	Г
15 ≥ 5	2 < 2	7 > -3	-10 ≤ 10

Правильна відповідь: «В»

4. Яке з поданих чисел задовольняє нерівність х²+2х+1 ≤ 0?

А	Б	В	Г
-1	0	1	2

Правильна відповідь: «А»

5. Скільки цілих чисел задовольняє подвійну нерівність -1 ≤ х ≤ 1?

А	Б	В	Г
Одне	Два	Три	Чотири

Правильна відповідь: «В»

6. Виберіть проміжок, якому належить число 1,37.

А	Б	В	Г
[-2;3]	(-∞;1,37)	(1,37;2]	(-1,37;1,36]

Правильна відповідь: «А»

7. Виберіть нерівність, яка не має розв’язків.

А	Б	В	Г
\|х\| > -3	х < -3	7 - \|х\| < 0	х² < 0

Правильна відповідь: «Г»

8. Яке найбільше число є розв'язком нерівності х² - 2х ≥ х² +2?

А	Б	В	Г
2	1	0	-1

Правильна відповідь: «Г»

9. Знайдіть область визначення функції у = +

А	Б	В	Г
(-∞;0)	[0;+∞)	(0;+∞)	(-∞;0) Перегляд файлу Попередній слайд 1 / 28 Наступний слайд Зміст слайдів Номер слайду 1 АЛГЕБРА 9-А КЛАСТема уроку: Розв’язування лінійних нерівностей з однією змінною Номер слайду 2 Мета: відтворити знання про лінійні нерівності з однією змінною; удосконалювати вміння учнів розв’язувати нерівності з однією змінною; формувати навички самостійної роботи; розвивати увагу, пам’ять, мислення, культуру математичного мовлення; виховувати самостійність, активність, дисциплінованість, інтерес до математики. Тип уроку: формування та удосконалення вмінь та навичок. Обладнання: інтерактивна дошка, проектор, роздатковий матеріал: піктограми настрою, картки контролю знань, картки лото, мультимедійна презентаціяrr Номер слайду 3 №з/п. Назва завдання. Кількість балівІ. Тестові завдання 1. 2. 3. 4. 5. 6. ІІ. Перевірка домашнього завдання 1. 2. ІІІ. Завдання із самоперевіркою 1. 2. 3. 4. 5. 6. 7. 8. 9. ІV. Математичне лото Картка самоконтролю. Прізвище, ім’я учня(учениці)__________________________Оцінка за урок = загальна кількість балів𝟐 = ________ Номер слайду 4 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} Актуалізація опорних знань. Діагностика виконання домашнього завдання. Виконання тестових завдань з усним обговоренням1. Установіть відповідність між висловленням (1-4) та наслідком із нього (А-Г) (кожна правильна відповідь оцінюється 0,5 балів)Правильна відповідь: 1-Б, 2-Г, 3-А,4-В{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}1a > b. Аa – b = 02a ≥ b. Бa – b > 03a = b. Вa – b ≤ 04a ≤ b. Гa – b ≥ 0 Номер слайду 5 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 2. Відомо, що a > b. Які з поданих нерівностей є правильними? (кожна правильна відповідь оцінюється 0,5 балів)Правильна відповідь: А, Б, Г, Д{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВ3a > 3ba – 70 > b - 70a – 5 > b – 10 ГДЕ-6a < -6b𝒂𝟕 > 𝒃𝟕a – 6 < b - 6{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВ3a > 3ba – 70 > b - 70a – 5 > b – 10 ГДЕ-6a < -6ba – 6 < b - 6rrrrr Номер слайду 6 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 3. Серед наведених нерівностей укажіть лінійну нерівність з однією змінною. (кожна правильна відповідь оцінюється 0,5 балів)Правильна відповідь: А, Г. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВ2 < 𝟑х+𝟐𝟒 ≤ 6𝟓х - 4 < 9х² – 5 > 0 ГД𝟐𝟑х – 5 ≤ х + 6х + у > 8{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВх² – 5 > 0 ГДх + у > 8rrrrr Номер слайду 7 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 4. Які з поданих чисел є розв’язками нерівності 3х + 1 > 2 ? (кожна правильна відповідь оцінюється 0,5 балів) Правильна відповідь: Г, Д. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД-2- 𝟏𝟑00,54{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД-200,54rrrrr Номер слайду 8 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 5. Які з поданих нерівностей рівносильні? (кожна правильна відповідь оцінюється 0,5 балів) Правильна відповідь: «Б». {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВ5х+1>0 і 5х>13х<0 і х<0-2х>0 і х>0rrrrr Номер слайду 9 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 6. Установіть відповідність між нерівністю (1-5) та числовим проміжком (А-Д). (кожна правильна відповідь оцінюється 0,5 балів) Правильна відповідь: 1-Д, 2-Г, 3-А, 4-В, 5-Б. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}1х < 5 А(-∞;-5)2х ≥ 5 Б(0;5]3х < -5 В(5;+∞)4х > 5 Г[5;+∞)50 < х ≤ 5 Д(-∞;5)rrrrr Номер слайду 10 2. Перевірка домашнього завдання № 5.7 (ст.36)Відповідь: 3) (-∞;8,99]№ 5.20 (ст.37)Відповідь: 1. (-∞;-3); 2. (-∞;10]; 3. (4;+∞); 4. [5,5;+∞).(правильність № 5.7 – 1 бал; № 5.20 – 2 бали) Номер слайду 11 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Удосконалення знань3. Виконання тестових завдань з самоперевіркою 1. Виберіть правильну числову нерівність (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «В»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ0,2 > 2-1 < -25 ≥ 52,36 ≤ 1,1589 Номер слайду 12 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 2. Сумою нерівностей 5 > 3 і 2 > -1 є нерівність (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «В»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ4 > 54 < 57 > 27 ≥ 2 Номер слайду 13 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 3. Укажіть строгу нерівність (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «В»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ15 ≥ 52 < 27 > -3-10 ≤ 10 Номер слайду 14 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 4. Яке з поданих чисел задовольняє нерівність х²+2х+1 ≤ 0? (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «А»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ-1012 Номер слайду 15 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 5. Скільки цілих чисел задовольняє подвійну нерівність-1 ≤ х ≤ 1? (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «В»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГОдне Два Три Чотири Номер слайду 16 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 6. Виберіть проміжок, якому належить число 1,37. (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «А»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ[-2;3](-∞;1,37)(1,37;2](-1,37;1,36] Номер слайду 17 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 7. Виберіть нерівність, яка не має розв’язків. (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «Г»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ\|х\| > -3х < -37 - \|х\| < 0х² < 0 Номер слайду 18 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 8. Яке найбільше число є розв'язком нерівності х² - 2х ≥ х² +2? (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «Г»{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ210-1 Номер слайду 19 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} 9. Знайдіть область визначення функції у = 𝟏х𝟐 +√х (правильна відповідь оцінюється в 1 бал) Правильна відповідь: «В» {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ(-∞;0)[0;+∞)(0;+∞)(-∞;0) 󠅰∪ (0;+∞){2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГ(-∞;0)[0;+∞)(0;+∞) Номер слайду 20 «МАТЕМАТИЧНЕ ЛОТО» Номер слайду 21 Томас Гарріот – англійський астроном, математик, етнограф і переводчик. Знаки нерівності (строгі знаки) >, < з’явилися вперше 1631 року в роботі вченого Томаса Гарріота, яка була видана посмертно. До цього писали слова «більше», «менше». ІСТОРИЧНА ДОВІДКА Номер слайду 22 Джон Валліс – англійський математик Символи ≥ , ≤ (нестрогі знаки нерівності) запропонував Валліс (1670). Спочатку риска була вище за знак порівняння, а не під ним, як зараз. Номер слайду 23 П’єр Бугер – французький математик Широке розповсюдження нестрогі знаки нерівностей отримали після підтримки французьким математиком П. Бугер (1734), у якого вони набули сучасного вигляду Номер слайду 24 1557 року знак рівності запропонував Роберт Рекорд; зображення символу було набагато довше, ніж зараз. Автор пояснював, що не має в світі нічого більш рівного, чим два паралельні відрізки рівної довжини. Деякий час поширенню символу Рекорда заважала та обставина, що з античних часів такий самий символ використовували для позначення паралельності прямих; урешті було вирішено символ паралельності зробити вертикальним. Номер слайду 25 Готфрід Вільгельм Лейбніц – німецький математик У континентальній Європі знак рівності ввів Лейбніц. Номер слайду 26 РЕЛАКСАЦІЯ ГАРНИЙ НАСТРІЙСЕРЕДНІЙ НАСТРІЙПОГАНИЙ НАСТРІЙ Номер слайду 27 Домашнє завдання. Повторити §5, виконати №5.25 Номер слайду 28 Дякуємо за увагу! zip Завантажити Зберегти на потім Додав(-ла) Мацко Галина Василівна Пов’язані теми Алгебра, Інтегровані уроки Додано 3 березня 2019 Переглядів 1827 Оцінка розробки Відгуки відсутні Безкоштовний сертифікат про публікацію авторської розробки Щоб отримати, додайте розробку Додати розробку Рекомендовані матеріали docx 2600 4.7 Тестові завдання ЗНО з теми "функції" pptx 1466 0 Урок "Множення многочлена на многочлен" docx 6524 5 Самостійна робота "Знаходження площі криволінійної трапеції" docx 943 0 Контрольна робота " Функції. Їх властивості і графіки" Схожі матеріали docx 2699 0 конспект + презентація zip 3052 5 Числові функції. Область визначення та множина значень функції docx 22098 5 Розв’язування задач за допомогою систем лінійних рівнянь із двома змінними pptx 3300 5 Застосування визначеного інтеграла docx 25176 4.7 Розвязування задач з параметрами Поділитись матеріалом facebook 0 viber 0 telegram 0 Twitter 0 Google+ 0 Завантажити Зберегти на потім Перевірка виданих документів Вкажіть номер документа (використовуйте кириличну розкладку) Підвищення кваліфікації Підвищення кваліфікації Вебінари Конференції Курси Розділи Журнал Бібліотека розробок Тести Лабораторні роботи Проєкти Конкурси Олімпіади Штучний інтелект для вчителів Курси англійської мови Про нас Про «На Урок» Співпраця закладів освіти Зворотний зв'язок Інше Вхід для учнів (naurok.ua) Матеріали до свят Конкурс «Фантастична п’ятірка» © 2017-2024, ТОВ «На Урок» Угода користувача \| Умови користування \| Політика конфіденційності Реєстрація на сайті «На Урок» Зареєструватись за допомогою Facebook Зареєструватись за допомогою Google або Прізвище Ім'я Email Пароль Реєструючись, ви погоджуєтеся з угодою користувача та політикою конфіденційності. Вже зареєстровані? Спробуйте увійти Давай дружити! Оновлення «На Урок» — в кожну стрічку Facebook «На Урок». Освітній інтернет-проект Дякую, Я вже давно з вами Розсилка «На Урок» Ми надсилатимемо наші цікаві та дуже корисні статті щоп’ятниці Ваш e-mail Дякуємо! Ми будемо тримати Вас в курсі!