Самостійна робота "Знаходження площі криволінійної трапеції"

Про матеріал

Самостійна робота з теми "Знаходження площі криволінійної трапеції" складається з двох частин: перша - тестові завдання на знаходження правильної формули для знаходження площі, друга частина - диференційовані завдання на обчислення площі заштрихованої фігури (1 - 2 рівні: оцінка до 8 балів, 3 - 4 рівні до 12 балів). В завданнях використовувались Збірники для ЗНО.

Перегляд файлу

Самостійна робота

Тема: Знаходження площі плоскої фігури

В – 1 1 частина

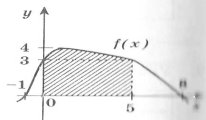
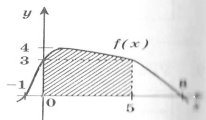
1. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\СР1 001.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

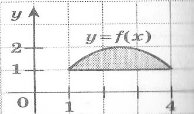
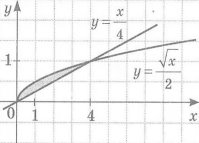
2. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\ср1 002.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

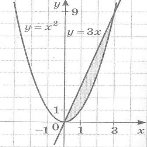
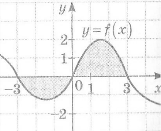
3. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\ср1 003.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

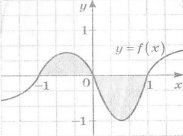
4. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\ср1 005 — копия.jpg$
Б) S = dx –
В) S = dx –
Г) S = 2 dx
Д) S = 2 dx

5. Встановіть відповідність між заданими фігурами (1-4) і формулами для обчислення їхньої площі (А-Г)

1.. у = х + 2, у = 0, х = 0.	А) dx
2. у = – х + 2, х = – 2, х = 1, у = 0.	Б) dx
3. у = х – 2, х = – 2, у = 0.	В)dx
4. у = – х – 2, х = – 2, х = 1.	Г)dx

2 частина

1 – 2 рівні

3 – 4 рівні

Обчислити площу фігури, обмеженої лініями:

1. у = 2х – 3, х = –2, х = 1, у = 0;

2. у = , х = 0, х = , у = 0;

3. у = х², у = 4.

1. у = х + 1, х = – 1, у = 3;

2. у = х² – 1, у = 1 – х² ;

3. у = – , х – у = 6.

Самостійна робота

Тема: Знаходження площі плоскої фігури

В – 2 1 частина

1. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\СР1 001.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

2. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\ср1 002.jpg$
Б) S = dx
В) S = dx
Г) S = dx
Д) S = dx

3. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S = dx	$C:\Users\Lenovo\Desktop\СР1\ср1 004 — копия.jpg$
Б) S = - ) dx
В) S = dx
Г) S = - ) dx
Д) S = dx

4. Укажіть формулу, за якою обчислюється площа заштрихованої фігури:

А) S =2 dx	$C:\Users\Lenovo\Desktop\СР1\ср1 005.jpg$
Б) S = dx –
В) S = dx –
Г) S = 2 dx
Д) S = 2 dx

5. Встановіть відповідність між заданими фігурами (1-4) і формулами для обчислення їхньої площі (А-Г)

1.. у = х + 2, у = 0, х = 0.	А) dx
2. у = – х + 2, х = – 2, х = 1, у = 0.	Б) dx
3. у = х – 2, х = – 2, у = 0.	В)dx
4. у = – х – 2, х = – 2, х = 1.	Г)dx

2 частина

1 – 2 рівні

3 – 4 рівні

Обчислити площу фігури, обмеженої лініями:

1. у = 2х – 3, х = –2, х = 1, у = 0;

2. у = , х = 0, х = , у = 0;

3. у = х², у = 4.

1. у = х + 1, х = – 1, у = 3;

2. у = х² – 1, у = 1 – х² ;

3. у = – , х – у = 6.

Середня оцінка розробки

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0

Загальна:

5.0

Всього відгуків: 2

Оцінки та відгуки

Яковець Ліна 06.04.2021 в 10:31

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0
Федоренко Тетяна Вікторівна 19.02.2021 в 06:47

Загальна:

5.0

Структурованість

5.0

Оригінальність викладу

5.0

Відповідність темі

5.0