Відкритий урок "Рахуємо без проблем"
На цьому уроці йде закріплення матеріалу "Дії з натуральними числами". В папці представлений не тільки сам урок, але і тести (як в паперовому так і компьютерному варіанті) для перевірки знань учнів.Презентація озвучена
- без проблем.pptx pptx
- .docx docx
Урок в 5 класі.
Тема. Дії з натуральними числами.
Рахунок і обчислення – основа порядку в голові.
Песталоцці І.
Мета:
- Сформувати в учнів уміння раціональних усних обчислень.
- Розвинути вміння застосовувати раціональні обчислення при розв’язуванні нестандартних завдань.
- Виховувати культуру математичної грамотності.
Тип уроку: узагальнення та систематизація знань
Форми роботи: фронтальна, індивідуальна.
Урок проводиться на базі компьютерного класу.
1 етап.(Актуалізація опорних знань) Вчитель демонструє учням презентацію, яка нагадує деякі властивості арифметичних дій.
2 етап. (Фронтальна перевірка знань) Діти самостійно виконують тести на комп’ютерах (тести додаються), і свої результати повідомляють учителю.
3 етап. Удосконалення умінь та навичок з теми.
Учитель пояснює алгоритми розв,язування нестандартних вправ.
- Вправи в яких учень повинен розставити знаки дій та дужки, щоб отримати правильну відповідь, допомагають учневі не тільки розвинуті логіку, але і змушують його застосувати свої вміння і навчити усного рахунку, аналізуючи умову.
Як приклад, краще запропонувати учням схожі вправи, які відрізняться лише відповіддю.
5 5 5 5=11 5 5 5 5=15
В кожній вправі ми будемо проводити аналіз «з кінця», а саме:
В першому прикладі, щоб з п’яти отримати 11 треба або до 5 додати 6, або 55 поділити на 5. Оскільки в другому випадку залишається зайва 5, його відкидаємо. Щоб в першому випадку отримати шість треба або до 5 додати 1 (це можливо бо 5÷5=1) або 30:6 (що не підходить). Отже, відповідь
5 5+5+5=11
Аналізуючи разом с дітьми другий приклад, ми отримаємо:
5∙5-(6+5)=15
В той час, як вчитель з усім класом розбирає приклад, обдаровані діти можуть отримати завдання для самостійного розв’язання.
Для самостійної роботи запропонуємо наступні 2 вправи:
5 5 5 5=25 5 5 5 5=24
- Дуже добре застосовувати свої вміння діти можуть при розв’язуванні вправ на відновлення математичних дій, де замість цифр – зірочки. Такі вправи допомагають учням застосувати знання властивостей чисел на практиці ( в шкільних вправах це не дуже часто можна зробити). Як приклади, візьмемо 2 завдання.
![]()
![]() ∗∗∗∗-1=∗∗∗
∗∗∗∗-1=∗∗∗ 
Якщо перша вправа легка і робиться усно, то над другою треба трохи подумати. Але великих проблем у дітей, що рахують самостійно виникнути не повинно. Перша цифра другого числа або 1 або 2 ( це ми бачимо із результату – другий рядок допоміжних дій.
Останні дві цифри при множенні останньою цифрою дають 6. Це можливо, коли:
2∙8
2∙3
4∙4
7∙8
6∙6
4∙9
Отже, треба розглянути випадки:
48 42 42 43 44 47 48 46 44 49
2 8 3 2 4 8 7 6 9 4
Перший і четвертий відкидаємо ( вони не задовольняють першому рядку проміжних дій ) і розглянемо випадки:
42 42 42 42 44 44 47 47 48 48 46 46 44
18 28 13 23 14 24 18 28 17 27 16 26 19
44 49 49
24 14 24
Але оскільки в результаті виходить чотирицифрове число, то приклади, де другий множник менше 2 відкидаємо. Отримаємо:
42 42 44 47 48 46 44 49
28 23 24 28 27 26 25 24
Із цих випадків підходить лише 42∙23.
Учням пропонується самостійно розв’язати два приклади:
|
|
- Третій вид вправ – це магічні квадрати. Вони допомагають поєднати логіку та математичний рахунок.
Розглянемо приклад:
|
|
|
|
|
|
|
|
|
|
|
|
В квадрат розставити цифри від 1 до 9 таким чином,щоб по вертикальним, горизонтальним лініям та діагоналям сума чисел була однаковою і дорівнювала 15. Щоб розв’язати цю задачу, треба дітей наштовхнути спочатку на знаходження суми всіх чисел від 1 до 9 (45). Потім на те, що дану суму поділити на 3 ( три стовпчики, три рядки), та перебрати всі можливі випадки для отримання результату ділення – 15.
Ці випадки:
9 1 5 9 4 2 8 3 4 8 2 5 8 1 6 7 2 6 7 3 5 6 5 4
Залишається лише розставити числа за правилом. Мі бачимо, що з 9 можливо всього два випадки, як і з 7. Отже ці числа не можуть стояти кутах квадрата, та в центрі. Разом один з одним теж, тому є 1 випадок (інші лише інтерпретація даного).
|
|
7 |
|
|
9 |
|
|
|
|
|
|
Із зазначених вище трійок бачимо, що в центрі можуть відповідати 9 і 7 лише два числа 5 і 2.
Перевіримо обидва:
|
|
Із того, що залишилося підбираємо решту чисел:
|
|
І хоча магічних квадратів не так багато, є різні їх інтерпретації.
Такі вправи можна запропонувати класу:
№1. Розставте числа 6,5,4,3,2,1 в кружках таким чином, щоб сума вздовж кожної прямої дорівнювала 12.
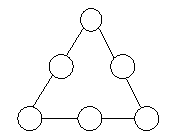
А наступну задачу запропонуйте обдарованим учням.
№2. Розставте числа 1,9,0,8 так, щоб в горизонтальних рядках отримати числа, що є квадратами, а сума чисел, розташованих в центральносиметричних кружках була однаковою.
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
- І останній тип вправ, який треба розглянути на уроці, це розв’язання криптоарифметичних прикладів. Ці завдання в найбільшій мірі використовують властивості чисел та дій над ними. Починати треба з нескладних. Два таких приклада ми розбираємо в класі. Перший, як завжди, пояснює вчитель, а другий він робить за допомогою дітей.
![]()
![]()
![]()
Не важко здогадатись, бо Б=1. Оскільки ми до двоцифрового числа додали одноцифрове число і отримали трицифрове. То таке можливо, коли А=9. Отже,маємо:
![]()
![]()
![]()
Звідси можна побачити, що В=0.
Наступний приклад більш складний, але розв’язуючи його з класом, ви побачите, що для деяких учнів ця складність не перешкодить.
![]()
![]()
![]()
Відразу можна помітити, що А=1, Е=0.
Оскільки C+С отримали в кінці В, то це означає, що В – парне число, тобто 2;4;6;8.
Перевіримо випадки:
В=2,4 не можливо, тому що на початку чисел, В повинно бути ![]()
В=6, тоді С=3 або С=8.Непарне С![]()
Залишаєтося розглянути випадок В=8, тоді С=4 або с=9.
Якщо С=4, то Д або 2 або 7, це не задовольняє першому стовпчику.
Якщо С=9, то Д 4 або 7. Для першого стовпчика підходить 7.
Отже, відповідь:
![]()
![]()
Для самостійного розв’язування запропонувати учням класу подібний приклад:
![]()
![]()
А для обдарованих: У-Р=А÷В=Н∙Е=Н+И=Е
4 етап. Підбиття підсумків і висновки.
В підсумках уроку обов’язково оцінити дітей за їх ідеї та думки, бо людина, яка мислить самостійно, набагато дорожча за людину, яка правильно виконує завдання за алгоритмом.
5 етап. Домашнє завдання.
Додому задаються завдання подібні прикладам, що рзв,язувались на уроці:
№1. 5 5 5 5=1
№2 Розставити числа 1,2,3,4,5,6,7,8,9 в кружках так, щоб сума на кожній стороні була 20.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() №3
№3 ![]()
![]() №4
№4 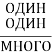


про публікацію авторської розробки
Додати розробку
















