Відкритий урок з алгебри 11 клас "Визначений інтеграл"

![]()


Мета уроку
1. Освітня:
- Узагальнити поняття «первісна» та «інтеграл»;
- Закріпити набуті навички у застосування визначеного інтеграла до розв’язування задач геометричного та фізичного змісту;
- з'ясувати де і для чого потрібен інтеграл.
2. Розвиваюча:
- Сприяти розвитку в учнів вміння застосовувати отримані знання, аналізувати і узагальнювати отриману інформацію;
- Розвивати комунікативну та інші ключові компетентності;
- Розвивати зацікавленість учнів у вивченні матеріалу за допомогою інформаційних технологій (відео проектор, презентація PowerPoint).
- Виховна:
- Продовжувати роботу над вихованням в учнів працездатності, самостійності, уважності;
- Прививати любов до точних наук.
Завдання уроку:
- Закріпити отримані знання з теми «Інтеграл»;
- Навчити самостійно працювати;
- Вдосконалити вміння аналізувати та оцінювати власні можливості, здібності, навички та знання;
- Навчити взаємодіяти.
Методи навчання:
- Евристичний.
Тип уроку: комбінований.
Обладнання: комп’ютер, відеопроектор, екран, дидактичні матеріали, картки самооцінювання, рамка з ватманом для картини.

Етапи уроку:
- Організаційний момент – 1 хв.
-
Актуалізація опорних знань – 8 хв.
- Бліц опитування (картки) – 5 хв.
- Відтворення формул знаходження площ криволінійних трапецій (квіти-формули) – 3 хв.
- Перевірка домашнього завдання – 5 хв.
- Розв’язування різнорівневих завдань (застосування визначеного інтеграла до розв’язування задач геометричного та фізичного змісту) – 23 хв.
- Підсумок уроку – 2 хв.
- Повідомлення домашнього завдання – 1 хв.
В одном мгновенье видеть вечность,
Огромный мир – в зерне песка,
В единой горсти – бесконечность,
И небо в чашечке цветка.
С.Маршак
Хід уроку:
І. Організаційний момент
(Перевірка готовності учнів до роботи. Оголошення теми і мети уроку)
(Слайди № 1- 2 тема і мета уроку).
- Ми з вами вивчили тему «Інтеграл» і сьогодні маємо пригадати базові поняття, закріпити навички знаходження первісних, обчислення інтегралів та їх застосування. А також створити картину уроку.
Візьміть із файлу, що знаходиться перед вами бланк самооцінювання, впишіть у нього своє прізвище. Бланк містить критерії оцінювання кожного виду роботи. Не забувайте протягом уроку виставляти до бланку отримані бали.

ІІ. Актуалізація опорних знань
Першою на нашій картині з’явиться хмарина-епіграф (цитую).

Щоб дізнатись, хто автор цього вірша, ви маєте розв’язати тестові завдання.
1) Бліц опитування (тести)
(Слайд № 3 робота з бланками відповідей).
- Візьміть із файлу тести і бланки відповідей та заповніть бланки, відзначивши правильну відповідь. Кожне завдання оцінюється в 1 бал. Максимальна кількість балів, яку ви можете отримати – 6 б.

Тест (початковий рівень)
- Якщо функція F(x) є первісною для функції f(x), то справджується рівність:
А) F(x) = f(x); Б) f(x) = F(x); В) f(x) = F(x); Г) f(x) = F(x) dх.
-
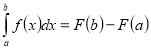 – це теорема:
– це теорема:
А) Больцано – Коші;
Б) Бойля – Маріотта;
В) Ньютона – Лейбніца;
Г) Вейєрштрасса.
- Яка з функцій є первісною для функції f(x) = 4x3?
А) F(x) = x3 + 2x; Б) F(x) = x4 + 4; B) F(x) = x4 + x; Г) F(x) = x3 + 3.
- Яка з функцій є такою, що f(x) = cosx?
А) f(x) = sinx; Б) f(x) = – sinx; В) f(x) = – cosx; Г) f(x) = ctgx.
-
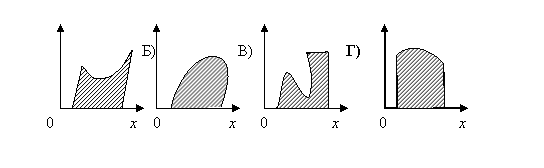
 Яку із зображених фігур можна назвати криволінійною трапецією?
Яку із зображених фігур можна назвати криволінійною трапецією?
-
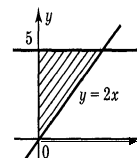 Якими лініями обмежена фігура, зображена на малюнку?
Якими лініями обмежена фігура, зображена на малюнку?
А) f(x) = 2х, у = х, у = 0;
Б) f(x) = 2х, у = 5х, х = 0;
![]() В) f(x) = 2х, х = 5, у = 0;
В) f(x) = 2х, х = 5, у = 0;
Г) f(x) = х, у = 0, у = 5.

Бланк відповідей Бланк правильних відповідей
|
|
А |
Б |
В |
Г |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
|
А |
Б |
В |
Г |
|
1 |
М |
|
|
|
|
2 |
|
|
А |
|
|
3 |
|
Р |
|
|
|
4 |
Ш |
|
|
|
|
5 |
|
|
|
А |
|
6 |
|
|
К |
|
(роздаю бланки із вирізаними комірками правильних відповідей)
- Правильні відповіді утворили прізвище відомого дитячого письменника, вірш якого буде епіграфом до картини нашого уроку.
2) Перевірка знання формул
Відтворення формул
На клумбі біля школи
Весняним днем чудовим
Метелики в квітках собі гуляли.
Одному з них, на лихо всім
Дві бабочки припали до душі.
І він, щоб швидше відгадати,
Кого із двох собі обрати,
Надумав їм букет подарувати.
Та замість крокусів і мальв
Букет із формул він зібрав.
- І нащо нам букет із формул? –
Обурено спитали двоє.
Красуням вишуканим він
Так філософськи відповів:
В усіх квіток, які зірву я
Первісний запах незабутній.
Проінтегрую їх в букети,
Що вам любов свою довести.
Коли квіток зів’яне цвіт,
Чи лишиться від квітки слід?
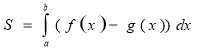 ,
, 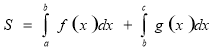 ,
,
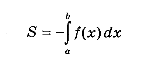
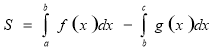 ,
,
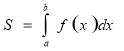

Щоб зберегти первісність весняних квітів, створимо на картині клумбу із квіток-формул. Співставте, будь ласка, графічні зображення криволінійних трапецій із відповідними формулами, та прикріпіть їх.


ІІІ. Перевірка домашнього завдання
На інтегральнім дереві синицям
Сьогодні вранці було чим поживиться.
Домашніх вправ плоди такі корисні:
Усі дозрілі, смачні і не кислі.
А може вони просто для насмішки
Плоди лиш понадзьобували трішки?
- Наступне завдання полягає у відтворенні втрачених елементів виконаного завдання. Із цим завданням гарно впорається той, хто самостійно виконував домашнє завдання. Візьміть із файлу картки-плоди і допишіть невистачаючі частини. Потім прикріпіть їх на інтегральне дерево картини.

Поставте кількість отриманих балів у відповідну графу картки самооцінювання.
IV. Робота з різнорівневими завданнями
- Де і для чого застосовують інтеграли?
Тепер і ви спробуйте свої сили у розв’язування вправ. Візьміть конверт із написом «Різнорівневі завдання», оберіть картку, яка відповідає вашому рівню й розв’яжіть. Виконання завдання біля дошки додасть вам 1 бал.
Картки
А. Середній рівень (кожне завдання по 4 б)
|


В. Достатній рівень (кожне завдання по 5 б)
|


С. Високий рівень (кожне завдання по 6 б)
|

Розв’язання.
А.1.
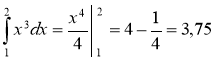
А.2.
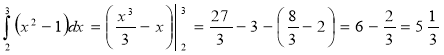 (од.2)
(од.2)
Відповідь: ![]() од.2
од.2
А.3.
![]() (од.2),
(од.2), 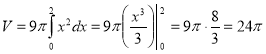 (од.3)
(од.3)
Відповідь: 24 од.3
В.1.
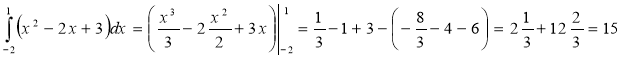 В.2.
В.2.
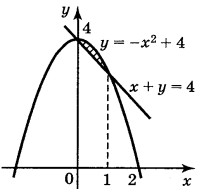 у = – х2 + 4, у = 4 - х:
у = – х2 + 4, у = 4 - х:
1) Знайдемо межі інтегрування:
– х2 + 4 = 4 - х;
х2 – х = 0;
х(х – 1) = 0;
х1 = 0, х2 = 1.
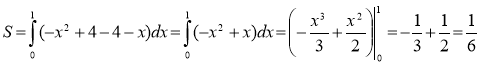 (од.2)
(од.2)
Відповідь: ![]() од.2
од.2
В.3.
![]() (од.2);
(од.2); 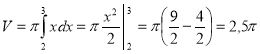 (од.3)
(од.3)
Відповідь: 2,5 од.3
С.1.
s(t) = ![]() dt =
dt = 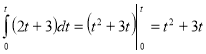
t2 + 3t = 36; t2 + 3t – 36 = 0; t1 = 6 c, t2 = – 9 – ст. к.
Відповідь:6 с.
С.2.
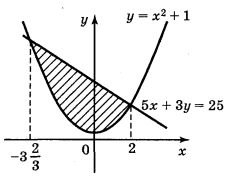 Знайдемо абсциси точок перетину ліній
Знайдемо абсциси точок перетину ліній
у = х2 + 1 і у =![]() :
:
х2 + 1 =![]() ; 3х2 + 3 = 25 – 5х;
; 3х2 + 3 = 25 – 5х;
3x2 + 5x – 22 = 0; x1 = 2; x2 = ![]() .
.
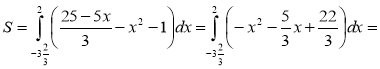
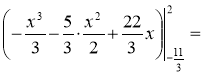
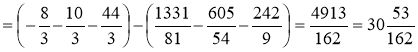 (од.2)
(од.2)
Відповідь: ![]() од.2
од.2
С.2.
Площа інтегрування: S = π (x2 + 1) 2 = π (x4 + 2x2 + 1)
V = 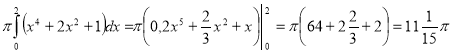 (од.3)
(од.3)
Відповідь: ![]() од.3
од.3
- Захист проекту
- Хто підготував проект про інше застосування інтеграла?
(Захист учнівського проекту "Застосування
інтеграла для розрахунку надійності ")


-
Підведення підсумків уроку
- Наш урок наблизився до завершення. Давайте проаналізуємо, чого ми досягли. Чи впорались ми із завданням, яке поставили на початку уроку?
Ми створили разом проект «Картина уроку»

- Проаналізуйте ваші бланки самооцінювання, підбийте загальну кількість балів і виставте оцінку, яку на вашу думку ви отримали. Аргументуйте оцінку, яку ви собі поставили за урок (2-3 учня).
- З останнього конверта, який знаходиться у вашому файлі, дістаньте "смайлик", яки відповідає вашому настрою наприкінці уроку, прикріпіть його до своєї картки самооцінювання та здайте мені. На перерві підійдіть із щоденником та отримайте зароблену оцінку.
- Повідомлення домашнього завдання
1. Повторіть правила інтегрування та таблицю первісних.
2. Виконайте завдання 11-13, 20 ст. 385-387 підручника
3. Підготуйтесь до контрольної роботи.
ДОДАТКИ ДО УРОКУ
Презентація до уроку

Презентація учнівського проекту



про публікацію авторської розробки
Додати розробку

 .
.