Використання інтеграла для обчислення об’ємів
Про матеріал
Дану презентацію можна використовувати як при вивченні інтегралів, так і на позакласних заняттях та гуртках з математики. Можна доповнити заняття інтерактивними тестами та іграми Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



![Формула Ньютона - Лейбніца. Перш ніж перейти до вивчення теми: «Використання інтеграла для обчислення об’ємів», слід згадати формулу Ньютона – Лейбніца, яка допомагає обчислювати визначений інтеграл. Якщо функція y = f (x) неперервна на проміжку [a; b], то справедлива є дана формула. Формула Ньютона - Лейбніца. Перш ніж перейти до вивчення теми: «Використання інтеграла для обчислення об’ємів», слід згадати формулу Ньютона – Лейбніца, яка допомагає обчислювати визначений інтеграл. Якщо функція y = f (x) неперервна на проміжку [a; b], то справедлива є дана формула.](/uploads/files/3468970/416624/472587_images/3.jpg)
![Загальні основні властивості інтеграла. Для випадку a > b приймемо за означенням, що При a=b також за означенням, Якщо функція f(x) неперервна на [a;b] і c ∈ [a;b], то Інші властивості: Загальні основні властивості інтеграла. Для випадку a > b приймемо за означенням, що При a=b також за означенням, Якщо функція f(x) неперервна на [a;b] і c ∈ [a;b], то Інші властивості:](/uploads/files/3468970/416624/472587_images/4.jpg)
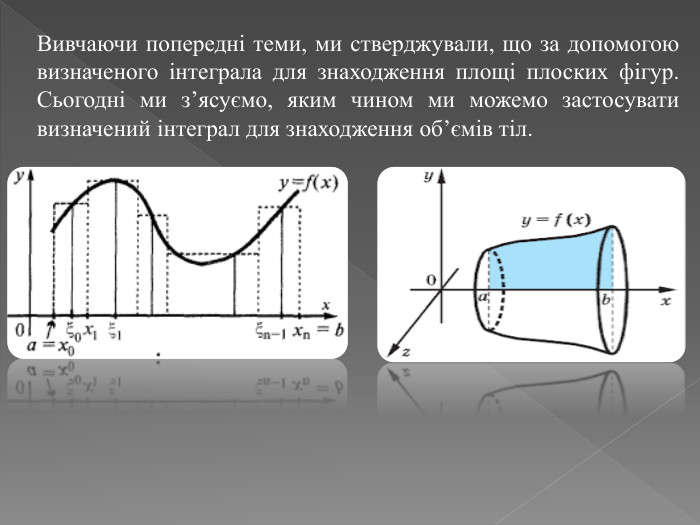

![Обчислення об'єму обертових тіл: Перший приклад, що варто розглянути, - це обчислення об'єму обертових тіл. Нехай маємо функцію f(x), яка визначена на відрізку [a,b] та не менше нуля на цьому інтервалі. Якщо цю функцію обернути навколо вісі x (або y), отримаємо об'єм тіла. Цей об'єм можна обчислити за допомогою наступного інтегралу: Обчислення об'єму обертових тіл: Перший приклад, що варто розглянути, - це обчислення об'єму обертових тіл. Нехай маємо функцію f(x), яка визначена на відрізку [a,b] та не менше нуля на цьому інтервалі. Якщо цю функцію обернути навколо вісі x (або y), отримаємо об'єм тіла. Цей об'єм можна обчислити за допомогою наступного інтегралу:](/uploads/files/3468970/416624/472587_images/7.jpg)
![Приклад 1: Нехай маємо функцію f(x)=x2 на інтервалі [0,1] Обчислимо об'єм тіла, яке утворюється обертанням цієї функції навколо вісі x: V = 𝝅𝟎𝟏𝒙𝟒𝒅𝒙=𝝅∙𝟏𝟓 = 𝝅𝟓 Приклад 1: Нехай маємо функцію f(x)=x2 на інтервалі [0,1] Обчислимо об'єм тіла, яке утворюється обертанням цієї функції навколо вісі x: V = 𝝅𝟎𝟏𝒙𝟒𝒅𝒙=𝝅∙𝟏𝟓 = 𝝅𝟓](/uploads/files/3468970/416624/472587_images/8.jpg)