Використання комп'ютерів у навчальному процесі як метод формування пізнавального інтересу молодших школярів

 

 

 

 

 

 

 

 

 

МОЖЛИВОСТІ ЗАСТОСУВАННЯ КОМП’ЮТЕРНИХ ТЕХНОЛОГІЙ НА УРОКАХ МАТЕМАТИКИ У ПОЧАТКОВИХ КЛАСАХ ПРИ ВИВЧЕННІ СЮЖЕТНИХ ЗАДАЧ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Харків  ̶  2018

ЗМІСТ

ВСТУП

1. Теоретичні основи вивчення сюжетних задач……………………….6
2. Методичні особливості вивчення сюжетних задач……………..….14
3. Досвід практичного застосування комп’ютерних технологій на уроках математики……………………………………………………20
4. Приклади практичного використання комп’ютерних технологій при вивченні сюжетних задач ……………………………………..……..26

ВИСНОВОК

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ВСТУП

У сучасному світі мабуть немає галузі, де б не використовувався комп’ютер і освітня галузь не є виключенням. Інтерес до вивчення предмету багато в чому залежить від того, як проходять уроки. Застосування комп'ютерної техніки на уроках дозволяє зробити урок нетрадиційним, яскравим, насиченим, наповнюючи його зміст знаннями з інших наочних областей, що перетворюють математику з об'єкту вивчення в засіб отримання нових знань.

Ефективність застосування нових інформаційних технологій на уроках математики обумовлена наступними факторами:

1)  різноманітність форм представлення інформації;

2)  висока степінь наочності;

3)  можливість моделювання за допомогою комп’ютера різноманітних об’єктів і процесів;

4)  звільнення від рутинної роботи, що відвертає увагу від  засвоєння основного змісту;

5)  можливість організації колективної та індивідуальної  дослідницької роботи;

6)  можливість диференціювати роботу учнів у залежності від рівня підготовки, пізнавальних інтересів та ін.; використовуючи сучасні інформаційні технології;

7)  можливість організувати комп’ютерний оперативний контроль і допомогу з боку вчителя;

8)  можливості комп’ютера дозволяють учню активно приймати  участь у процесі пізнання.

Об'єкт дослідження: комп’ютерні технології на уроках математики в

початковій школі.

Предмет дослідження: використання комп’ютерних технологій при вивченні сюжетних задач.

Мета дослідження полягає у визначенні впливу комп’ютерів на навчальну діяльність молодших школярів.

Вивчення психолого-педагогічної літератури з теми дослідження дозволило висунути таку гіпотезу: передбачається, що навчання за допомогою використання комп’ютерів можуть відігравати важливу роль у формуванні в учнів математичних знань при вивченні сюжетних задач.

У відповідності з метою та гіпотезою дослідження були визначені наступні завдання:

1. Здійснити аналіз наукових досліджень у галузі педагогіки,

психології та методики навчання математики щодо застосування інтерактивних технологій на уроках математики в початковій школі.

2. Обґрунтувати педагогічні умови використання інтерактивних

технологій на уроках з математики.

3. Перевірити ефективність умов використання комп’ютерів при вивченні сюжетних задач.

Для вирішення поставлених завдань і перевірки гіпотези були використані такі методи дослідження:

а) теоретичні: теоретичний аналіз, порівняння, узагальнення, класифікація, систематизація наукових джерел із філософії, психології, педагогіки та методики навчання математики, що дозволяють визначити та систематизувати основні положення, що складуть науково-теоретичну основу дослідження.

б) емпіричні: метод анкетування, тестування, бесіди, інтерв'ювання, узагальнення педагогічного досвіду, педагогічного спостереження, самоспостереження, опитування, статистичної обробки одержаних даних, які застосовуються для аналізу рівнів сформованості математичних уявлень та понять в учнів, дослідно-експериментальної перевірки результатів упровадження розробленого організаційно-методичного інструментарію, який має забезпечити формування математичних уявлень та понять в учнів початкової школи; педагогічний експеримент (констатувальний, формувальний етапи), математично-статистична обробка результатів дослідження - для аналізу одержаних даних, встановлення кількісних та якісних показників результатів дослідження.

Джерельну базу дослідження становить: наукові дисертації,підручники, посібники з фондів бібліотеки ХНПУ імені Г.С. Сковороди, національного університету імені В.Н. Каразіна та державної наукової бібліотеки імені В. Г. Короленка.

Практична значимість полягає в тому, що висновки та результати курсової роботи можуть бути використані в навчально-виховному процесі загальноосвітніх установ.

1. Теоретичні основи вивчення сюжетних задач

Поняття «задача» (від грец. Problema) є одним з найважливіших понять в психолого-педагогічних, природничо-математичних та методичних науках.

Значний внесок у розвиток методичного забезпечення по введенню даного поняття внесли Н.Г. Алексєєв, Г.А. Бал, Л.Л. Гурова, В.В. Давидов, Ю.М. Колягин, В.І. Крупич, Г.Л. Луканкін, Л.М. Фрідман, А.А. Столяр, П.М. Ерднієв та ін. Однак на сьогоднішній день немає єдиного підходу до визначення терміна «сюжетна задача».

Наприклад, у своїй статті «Про психологічний зміст поняття «завдання» Г.А. Бал [1] зазначає, що саме поняття «завдання» ніяк не можна визнати чітко визначеним. Даний термін використовується в психологічній і педагогічній літературі для позначення об'єктів, що відносяться до трьох різних категоріях: 1) до категорії мети дій (мета дії, вимоги завдання) суб'єкта; 2) до категорії ситуація (проблемна ситуація), що включає поряд з метою умови, в яких вона повинна бути досягнута; 3) до категорії словесної формулювання (формулювання задачі) цієї ситуації.

Г.А. Бал [1] вважає, що в психологічній літературі найбільш поширене

вживання терміна «задача» для позначення другої категорії. Аналізуючи

різні визначення, Г.А. Бал [1] наводить наступну послідовність визначень завдання у другому значенні цього слова:

1. Завдання є ситуація, що вимагає від суб'єкта деякої дії.

2. Розумова задача – ситуація, що вимагає від суб'єкта деякої дії, спрямованого на знаходження невідомого на основі використання його зв'язків з відомим.

3. Проблемна задача, або проблема,  ̶  ситуація, що вимагає від суб'єкта

деякої дії, спрямованого на знаходження невідомого на основі використання його зв'язків з відомим в умовах, коли суб'єкт не володіє способом (алгоритмом) цієї дії.

Л.Ф. Фрідман [28], підтримуючи думку Г.А. Балла з даного питання, зазначає, що завдання виникає на основі проблемної ситуації, притому з допомогою знаків якого-небудь мови як модель даної проблемної ситуації. З цим підходом не згодні А.В. Брушлинский [4] і А.М. Матюшкін [10]. Наприклад, А.М. Матюшкін обґрунтовує свою незгоду необхідністю розрізняти поняття: «проблемна ситуація» і «задача». «Очевидно, - пише він, - що поняття «проблемна ситуація» і поняття «завдання»  ̶  це принципово різні поняття, що позначають різні психологічні реальності». Проблемна ситуація характеризується як специфічний вид взаємодії суб'єкта та об'єкта, а задача – як сформульоване у словесній або знаковій формі відношення між певними умовами, що характеризуються як «відоме», і тим, що потрібно знайти, характеризується як «шукане». А.В. Брушлинский на додаток до сказаного пише, що виникнення задачі на відміну від проблемної ситуації означає, що:

а) вдалося попередньо розчленувати дане і невідоме;

б) чітко фіксовані вихідні умови задачі (що дано, що відомо і т.д.) і вимога (що потрібно довести, знайти, визначити, обчислити і т.д.).

В цій характеристиці задачі дуже чітко представлена ​​її структура: дане (відоме) – невідоме (шукане), умова - вимога [4].

Компромісне рішення даної проблеми запропонував у своїх дослідженнях Ю.М. Колягин [7], який під задачею розуміє складну систему, що складається з суб'єкта (людини) і об'єкта - деякого безлічі, що містить взаємопов'язані через деякі властивості і відносини елементи. Автор по відношенню до суб'єкта виділяє стаціонарні та проблемні системи: система Р називається стаціонарною, якщо суб'єкту відомі всі елементи множини і відомі всі властивості елементів і відносини між ними, достатні для того, щоб він міг вважати безліч Р системою; система Р називається проблемної і позначається символом Рх, якщо суб'єкту невідомий хоча б один елемент, одна властивість або відношення, визначені в Р, необхідні для того, щоб він міг вважати Р системою.

Якщо існує потреба і можливість у встановленні даній людині елементів, властивостей і відносин з безлічі Р, проблемний характер якого зафіксований, то останнє стає задачею для даного суб'єкта. При цьому Ю.М. Колягин [7] зазначає, що задача існує незалежно від того, чи діє людина в напрямку її вирішення чи ні; необхідно лише усвідомлення людиною нестаціонарності даної системи Р і наявність цільового вказівки (або суб'єктивною потреби) до її перетворення.

С.Є. Царьова [30] у своїй роботі, відзначаючи відмінності між поняттями «текстова задача» і «навчальна задача», підкреслює, що текстова задача перетворюється на елемент навчальної задачі при усвідомленні та прийнятті учнями навчальної мети роботи із завданням. Те є текстова задача разом з навчальною метою, заради досягнення якої вона розглядається учнями, становить навчальне завдання.

На відміну від Ю.М. Колягина С.Є. Царьова [30] розглядає «систему», включає не «суб'єкта», а «навчальну мету». І якщо врахувати, що одна і та ж текстова задача може бути використана для досягнення кількох навчальних цілей, то, отже, вона може бути використана в якості елемента кількох навчальних завдань. Але, як правило, для досягнення навчальної мети використовується декілька текстових задач. Тобто навчальні завдання при збігу навчальної мети можуть відрізнятися конкретними текстовими задачами.

При визначенні поняття «сюжетна (текстова) задача» у методичній літературі особлива увага приділяється другого аспекту поняття «задача»,

Визначалися завдання як безліч, що складається з взаємопов'язаних через деякі властивості і відносини елементів. Однак і в цьому випадку можна говорити про відсутність єдиного підходу до визначення даного поняття. Наведемо деякі з них:

1. Під задачею у початковому курсі математики мається на увазі спеціальний текст, в якому змальована якась життєва ситуація, охарактеризована чисельними компонентами (А.В. Белошистая).

2. Під текстовими арифметичними задачами подрозумівають завдання, що мають житейська вмістом вирішуються за допомогою арифметичних дій (А.А. Столяр, В.А. Дрозд).

3. Математична задача – це зв'язний розповідь, в який введені значення деяких величин, і пропонується відшукати інші відомі значення величин, залежні від даних і пов'язані з ними певними співвідношеннями, зазначеними в умови (А.А Свечников).

4. Під сюжетною задачею розуміють завдання, в яких описано деякий життєвий сюжет (явище, подія, процес) з метою знаходження певних кількісних характеристик або значень (Л.П. Фрідман).

5. Текстова задача є опис деякої ситуації (ситуацій) на природному мовою з вимогою дати кількісну характеристику будь-якого компонента цієї ситуації, встановити наявність або відсутність деякого відносини між її компонентами або визначити вид цього відношення (Л.П. Стойлова, А.М. Пишкало, В.В. Статкевич).

6. Завдання увазі таку життєву ситуацію, яка пов'язана з числами і вимагає виконання арифметичних дій над ними. (М.А. Бантова)

7. Текстовою задачею називається опис деякої ситуації (явища, процесу) на природному і (або) математичній мові з вимогою або дати кількісну характеристику якогось компонента цій ситуації (визначити числове значення деякої величини по відомим числовим значення інших величин і залежностям між ними), або встановити наявність або відсутність деякого відносини між її компонентами або визначити вид цього відношення, або знайти послідовність необхідних дій (Т.Є. Демидова, А.П. Тонких).

8. Задача – це система даних і шуканих з їх властивостями і відносинами і з вказівкою на необхідність знайти шукані (Г.Т. Зайцев)

9. Всяка задача є вимога або на знаходження будь-яких знань про явищах дійсності (об'єктах і процесах) і їх характеристики, які вони мають в певних заданих в задачі умовах, або на отримання якогось шуканого практичного результату (побудувати щось, забезпечити виконання якихось умов тощо) (І.І. Ільясов).

10. Сюжетною задачею називається вимога знайти (встановити, визначити!) які-небудь характеристики деякого об'єкта по відомим іншим його характеристикам (Л.П. Фрідман).

11. Задача – це сформульоване словами питання, відповідь на який може бути отриманий за допомогою арифметичних дій (І.Н Моро).

12. Задача є непорожня множина елементів, на якому визначено заздалегідь дане відношення (О.Б. Єпішева, В.І. Крупич).

Таким чином, в сучасній методичній літературі під сюжетною задачею розуміють:

1. Текст, в якому змальована якась життєва ситуація (А.В. Белошистая, А.А. Свєчніков, А.А. Столяр, В.А. Дрозд)

2. Математичну задачу, в якій описаний певний життєвий сюжет (Л.П.Фрідман).

3. Життєву ситуацію (Т.Є. Демидова, А.П. Тонких, Л.П. Стойлова, А.М.Пишкало, М.А. Бантова).

4. Систему даних і шуканих (Г.Т. Зайцев)

5. Вимога (І.І. Ільясов, І.М. Моро, Л.П. Фрідман).

6. Непорожнє безліч елементів (О.Б. Єпішева, В.І. Крупич, Ю.М. Колягин).

Для того щоб розібратися у всьому різноманітті даних визначень, необхідно виявити основні ознаки даного поняття. Зокрема, у своїх дослідженнях Я.А. Пономарьов вказує на необхідність у різних визначеннях знайти загальне, істотне, а це загальне і буде основою визначення поняття «Задача» [15].

Дослідження основних ознак поняття «сюжетна задача» має на увазі визначення компонентів її структури. У всіх розглянутих визначеннях поняття «Задача» спостерігається багато спільного і в той же час - деякі відмінності. Загальним є структура задачі, що складається з даних, або відомих, з шуканих або невідомих об'єктів, з властивості об'єктів або відносин між ними, з мети або вимоги знайти шукане. Спільним є й те, що за родове поняття при визначенні завдання береться поняття, стосується структурі задачі (відношення між шуканими і даними, мета або вимога задачі). Різниця, головним чином, виявляється в тому, що в одних визначеннях в якості родового поняття береться структура задачі в цілому: відношення між умовою і вимогою (А.А. Матюшкін), модель проблемної ситуації (Л. Фрідман), в інших - кінцева її мета: мета (А.Н. Леонтьєв), вимога знайти шукане (С.О. Шатуновский). Але ця різниця, як ми вже відзначили, не впливає на структуру самої задачі. Тому є сенс структуру вважати вихідним положенням при визначенні поняття «завдання». Проте щодо компонентів самої структури задачі на сьогоднішній день також немає єдиного підходу.

Наприклад, А.А. Свєчніков [18] і В.В. Статкевич [26] виділяють в структурі сюжетної задачі наступні складові елементи:

а) умова:

- Словесне виклад сюжету, в якому в явній або в завуальованій формі вказана функціональна залежність між величинами;

- Числові значення величин або числові дані, про які йдеться в тексті задача;

б) питання, в якому пропонується дізнатися невідомі значення однієї або декількох величин.

З метою обгрунтування системи компонентів структури сюжетної задачі звернемося до досліджень Ю.М. Колягина [7] і В.І. Крупич [9], в яких авторами проведено найбільш грунтовне вивчення компонентів структури задачі.

Розглядаючи задачу як систему, Ю.М. Колягин виділяє в ній компоненти ACRB, де А - початковий стан (умова завдання); С - базис рішення задачі (теоретичне обгрунтування рішення задачі); R- рішення задачі (спосіб перетворення умови задачі для знаходження необхідного шуканого); В - кінцевий стан (вимога або мета задачі).

В.І. Крупич [9], грунтуючись на тому, що завдання несе в собі дві інформаційні складові: суб'єктивну і об'єктивну, виділяє в задачах зовнішню (інформаційну) і внутрішню структури.

Враховуючи підхід Ю.М. Колягина, В.І. Крупич [9] розглядає інформаційну структуру як систему, що складається з елементів ACRDB, де А – умову задачі (дані і відносини між ними); С - базис рішення задачі (теоретична і практична основа, необхідна для обгрунтування рішення задачі); R

- Основне відношення в системі відносин між даними і шуканими; D - спосіб, визначальний процес вирішення задачі; В - вимога або мета задачі (шукані (шукане) і відносини між ними).

На відміну від Ю.М. Колягина В.І. Крупич вводить до складу інформаційної структури компонент R (основне відношення в системі відносин між даними і шуканими), виявлення якого, на думку автора, є основоположним для побудови внутрішньої структури задачі, її елементів і зв'язків між ними.

Під внутрішньою структурою задачі В.І. Крупич [9] передбачає сукупність елементів аналізованої системи, зв'язків і видів зв'язків.

Кожна задача містить явні і неявні дані і залежності між величинами. Явні дані і залежності психологічно представляють собою сильні подразники. А неявні дані і залежності - слабкими подразниками, тому на них часом не звертають увагу. Необхідно в процесі вирішення сюжетної задачі не допускати подібної недбалості, так як, на перший погляд, несуттєвий факт є ключем до вирішення задачі.

Під логічної правильністю постановки задачі Л.М. Фрідман [28] увазі правильність з'єднання в задачі окремих її частин. При цьому він формулює такі вимоги до правильним завданням: 1) всі зазначені в задачі елементи предметної області повинні існувати; 2) всі зазначені в задачі відносини повинні бути дійсно визначені для тих елементів предметної області, для яких ці відносини задані в умові задачі; 3) область значень кожної із заданих в задачі змінних повинна бути не пустою; 4) всі твердження, задані в умові задачі, повинні бути істинними; 5) твердження, задані в умові задачі, не повинні суперечити один одному; 6) якщо мета задачі полягає в перетворенні деякої висказивательної форми в справжнє висловлювання, то в умові задачі повинні бути вказані хоча б деякі підстави для цього.

Логічно неправильними задачами називають задачі, які внутрішньо суперечливі. Незважаючи на те, що є можливість призвести формальне «рішення» деяких подібних задач, прийняти його не можна. Так як подібне «рішення» не має ніякого сенсу, відповіддю до таких задач може бути тільки «задача неправильно поставлена» або «рішення задачі неможливо».

Проведений аналіз дозволив нам виділити наступні компоненти структури сюжетної задачі:

1) елементи задачі:

а) відомі (явно задані);

б) невідомі (неконкретні, неявно задані): шукані (їх потрібно знайти або встановити); проміжні або допоміжні (знаходження яких не потрібно, але вони повинні бути знайдені в процесі пошуку шуканих);

2) величини, якими охарактеризовані елементи (скільки і які величини задані явно чи неявно в тексті задачі; характер кожного значення величини);

3) характер взаємозв'язків між елементами;

4) основне відношення між величинами;

5) стану (зміна значень величин, що характеризують її елементи);

6) ситуації (пропозиція, формалізоване основним ставленням, реалізованим в задачі).

З урахуванням перерахованих вище компонентів можна говорити про те, що сюжетна задача являє собою опис у вигляді сюжету деякої непорожньої множини елементів, на якому визначено задане відношення з вимогою знайти яку-небудь характеристику елемента, або встановити взаємозв'язок між елементами, або знайти послідовність необхідних дій.

 

 

 

 

 

 

 

 

2. Методичні особливості вивчення сюжетних задач

Під  математичною  задачею  розуміють  будь-яку  вимогу обчислити,  перетворити,  побудувати,  довести  або  дослідити  що-небудь,  що  стосується  кількісних  відношень  і  просторових  форм, створених людським розумом на основі знань про навколишній світ.

Серед  численних  математичних  задач  виділяють  задачі,  які називають по-різному: арифметичні, текстові, сюжетні. Усі ці задачі характеризуються  наступними  рисами:  

1) задачі  сформульовані  на природній мові (тому їх називають текстовими);

2) в них звичайно описується  кількісний  бік  якихось  явищ,  подій (тому  вони називаються  сюжетними);

3)  вони  являють  собою  задачі  на визначення  шуканого  значення  деякої  величини,  які  у  початковій школі  розв’язуються  арифметичними  способами(тому  їх  інколи називають  арифметичними). 

Таким  чином,  усі  ці  терміни розкривають одне й те саме поняття.

Ми  користуємося  терміном «сюжетна  задача». Під  сюжетною задачею ми розуміємо математичну задачу, в якій описаний деякий життєвий сюжет, а саме кількісний бік реальних процесів, явищ та ситуацій і міститься вимога знайти шукану величину за даними в задачі величинами та зв’язками між ними.

Питання про цілі розв’язування сюжетних задач є центральним в

методиці  навчання  математики.  Вони  з  одного  боку,  складають специфічний розділ програми, зміст якого учні повинні засвоїти, з другого – виступають як дидактичний засіб навчання, виховання і розвитку учнів. Проаналізувавши цілі розв’язування сюжетних задач, які були визначені В. А. Євтушевським, Н. О. Менчинскою та М. І. Моро, Є. С. Ляпіним, Л. М. Фрідманом, дістаємо висновку про те, що цілі розв’язування сюжетних задач за багато років не змінилися. На сучасному  етапі  розбудови  шкільної  математичної  освіти розв’язування  сюжетних  задач  у  навчанні  математики  переслідує наступні  цілі:  формування  в  учнів  загального  підходу,  загальних

вмінь  і  здібностей  розв’язання  будь-яких  задач;  пізнання  і  більш глибинне  оволодіння  математичними  поняттями,  що  вивчаються,  і деякими  загальнонауковими  і  загальножиттєвими  поняттями;  оволодіння поняттями моделі і моделювання і власно математичним моделюванням; розвиток  мислення,  кмітливості  учнів,  їх  творчого потенціалу.  Крім  загальних  цілей,  розв’язування  задач  виконує  у навчальному процесі ряд функцій: навчальні, розвивальні, виховуючи та контролюючі.

Навчальні  функції  задач  спрямовані  на  формування  системи математичних  знань,  умінь  і  навичок.  Через  систему  задач  учні вчаться  не  лише  застосовувати  здобуті  теоретичні  знання,  а  й переконуються на етапі мотивації у потребі здобуття нових знань; в процесі  розв’язування  задач  дістають  інформацію  про  методи  їх розв’язування.

Під  розвивальними  розуміють  функції  задач,  спрямовані  на формування в учнів науково-теоретичного, зокрема функціонального,  стилю мислення, на оволодіння ними загальними та специфічними розумовими  діями  та  прийомами  розумової  діяльності.  У  процесі розв’язування задач учні виконують різні розумові дії(аналіз, синтез, абстрагування,  порівняння,  конкретизацію  й  узагальнення), висловлюють судження і міркування.

Під виховуючими розуміють такі функції задач, що спрямовані на формування в учнів наукового світогляду, сприяють екологічному,  економічному,  естетичному  вихованню,  розвивають  пізнавальний інтерес,  позитивні  риси  особистості.  Як  виховний  спосіб,  задачі роблять  можливим  пов’язання  навчання  з  життям,  ознайомлення учнів  із  пізнавально-важливими  фактами.  Внутрішня  краса  самої математики, оригінальність прийомів розв’язування задач збуджують у  дітей  естетичні  почуття.  Треба  виділити  ще  й  контролюючу функцію  сюжетних  задач,  яка  спрямована  на  встановлення навченості,  рівня  загального  і  математичного  розвитку,  стану

засвоєння навчального матеріалу окремими учнями і класом в цілому.

Між  тим,  розв’язування  будь-якої  сюжетної  задачі поліфункціонально,  але  в  кожній  конкретній  задачі  вчитель  має виділяти  провідну  функцію  і  за  належної  цільової  установки домагатися її реалізації в першу чергу. Останнім часом на перший план методисти висувають функцію формування умінь розв’язування будь-яких  сюжетних  задач (Н. Б.  Істоміна,  І.  Б.  Нефьодова, С. М. Лук’янова,  В.  В.  Малихіна,  Л.  М.  Фрідман,  С. Є. Царьова). Формування  уміння  розв’язувати  задачі  розуміється  вченими,  як

формування загального уміння та окремих умінь розв’язувати задачі певних видів. При цьому процес навчання розв’язування сюжетних задач  повинен  бути  організований  так,  щоб  він  здійснював ефективний  вплив  на  розвиток  мислення  учнів  та  формування  їх особистості. Це положення знайшло відображення і у новій редакції Державного стандарту початкової загальної освіти (2010 р.). Таким чином, сюжетні задачі в початковому курсі математики реалізують навчальні,  розвивальні,  виховуючі  і  контролюючі  функції,  але основною є функція вироблення вмінь у їх розв’язуванні.

Таким чином, метою навчання розв’язування  задач у початковій школі  є  формування  у  молодших  школярів  умінь(загального  і окремих), що виявляється у можливості учнів успішно розв’язувати задачу  будь-якої  математичної  структури  початкового  курсу математики. Очевидно, що змістом навчання – є задачний матеріал початкового  курсу  математики,  а  саме  види  простих  і  складених задач. На матеріалі простих і складених задач діти знайомляться із структурою задачі, етапами її розв’язування, в них опрацьовується загальне уміння розв’язувати сюжетні задачі. На матеріалі «типових» задач –  задачах  на  знаходження  четвертого  пропорційного,  на

пропорційне ділення, на знаходження невідомих за двома різницями, на  подвійне  зведення  до  одиниці,  на  спільну  роботу,  на  рух здійснюється формування окремих умінь розв’язувати задачі.

Випускники  початкової  школи  повинні  вміти  розв’язувати  усі види простих задач та складені задачі на 3-4 дії одного чи різних ступенів. До програмного мінімуму відносяться «типові» задачі на знаходження  четвертого  пропорційного,  ускладнені  задачі  на знаходження четвертого пропорційного(задачі на подвійне зведення до одиниці), на пропорційне ділення, на знаходження невідомих за двома  різницями,  на  спільну  роботу,  задачі  на  одночасний  рух  в різних напрямках(назустріч та у протилежних напрямках). Задачі на спільну роботу, в яких продуктивність спільної праці знаходять дією віднімання,  та  задачі  на  одночасний  рух  в  одному  напрямку

(навздогін та з відставанням) та на неодночасний рух викликають цікавість в учнів з достатнім і високим рівнем навчальних досягнень, тому  вони  хоча  і  містяться  у  чинних  підручниках,  але  до обов’язкових результатів навчання не відносяться.

Основним методом навчання молодших школярів розв’язування сюжетних задач є частково-пошуковий метод або евристична бесіда, який полягає в тому, що вчитель заздалегідь готує систему запитань, відповідаючи на які учні самостійно знаходять спосіб розв’язування задачі.  Таким  чином,  методом  навчання  є  особливі  системи взаємопов’язаних навчальних задач, які побудовані із застосуванням сюжетних  задач  різноманітних  математичних  структур,  що пропонуються  у  чинних  підручниках  математики  для  початкової школи.  Системи  навчальних  задач  побудовані  таким  чином,  щоб спонукати  учня  виконувати  операції  порівняння,  абстрагування,  узагальнення, тобто спрямовані на розвиток мислення дитини. В них передбачено розкриття зв’язків між задачами різних видів і типів, з їх допомогою учні приучуються пов’язувати  кожну нову задачу з раніш вже розв’язаною.

Так,  при  навчанні  розв’язування  простих  задач  учням пропонується  порівняти  структуру  взаємно  обернених  задач,  що містять  співвідношення  додавання  або  віднімання  або  різницевого порівняння – з метою визначення відмінних ознак та їх впливу на розв’язання задачі. При введенні задач нових математичних структур (простих, складених, в тому числі й «типових») також здійснюється порівняння із задачами відомих математичних структур, визначення їх відмінності та її впливу на розв’язання задачі. Для узагальнення

способу  розв’язування «типових»  задач  використовуються різноманітні зміни умови або вимоги задачі і досліджується їх вплив на  розв’язання.  Отже,  формування  уміння  здійснюється  не  за допомогою  розв’язання  великої  кількості  задач,  а  через «дослідження»  опорної  задачі  засобом  спеціальної  системи  навчальних задач, яка містить такі обов’язкові елементи: розв’язання задачі  відомої  математичної  структури,  зміна/зміни  її  умови  або вимоги, дослідження впливу цих змін на розв’язання задачі. Учні під керівництвом вчителя  аналізують спосіб розв’язування  задачі на прикладі опорної задачі, узагальнюють його, а потім застосовують до наступних задач.

Також при ознайомленні першокласників з поняттям «задача», її структурними  компонентами,  застосовується  пояснювально-ілюстративний метод.

Очевидно,  що  зазначені  зміст  і  методи  навчання  визначають форми  навчання  молодших  школярів  розв’язування  задач – фронтальну  роботу  вчителя  з  класом  під  час  ознайомлення  із задачами певного виду або типу і індивідуальну роботу учнів над задачею. Під час індивідуальної роботи здійснюється диференціація навчання  через  диференціацію  дози  допомоги  учням  або диференціацію  задач  за  рівнем  їх  складності.  Диференціація  дози допомоги  може  реалізуватися  через  застосування  карток  з друкованою основою. Диференціація змісту навчання розв’язування задач  здійснюється  за  допомогою  визначення  обов’язкових  для розгляду усіма учнями питань та додаткових, які вивчаються за умов резерву часу або для поглибленого вивчення за рахунок варіативного компоненту  навчального  плану.  Очевидно,  що  до  обов’язкових питань  відноситься  навчання  розв’язування  задач,  що  входять  до програмного мінімуму.

Основним  засобом  навчання  молодших  школярів  розв’язувати сюжетні  задачі  є  репрезентативні  та  розв’язуючі  моделі. Репрезентативні моделі у вигляді короткого запису задачі(схема або таблиця) або у вигляді схематичного рисунка; розв’язуючі моделі у вигляді «дерева міркувань». Навчання учнів самостійного складання схематичних  рисунків  розпочинається  ще  в1-му  класі  під  час підготовчої  роботи  до  введення  поняття «задача» і  продовжується протягом  наступних  років  навчання.  Тому  можна  очікувати,  що нескладні  схематичні  рисунки  діти  змозі  виконати  самостійно,  а рисунки до задач дещо ускладненої математичної структури – під керівництвом  вчителя.  Іноді  для  економії  часу  на  уроці  під  час фронтальної роботи над задачею, схематичний рисунок виконується вчителем на дошці, на основі пропозицій школярів або пропонується дітям  у  готовому  вигляді.  Схеми  аналізу  або  синтезу – «дерева міркування» –  є  ілюстрацією  процесу  пошуку  розв’язування  і складаються вчителем разом із учнями під час фронтальної роботи над  задачею.  Схематичний  рисунок  та «дерево  міркувань»  виконуються учнями у разі потреби, під час самостійної роботи над задачею.

Також  до  засобів  навчання  розв’язування  задач  віднесемо дидактичні  матеріали:  тексти  пам’яток,  картки  з  друкованою основою. На перших етапах засвоєння порядку роботи над задачами (простими,  складеними),  під  час  самостійної  роботи,  учні користуються картками із текстом пам’яток, почергово виконуючи їх завдання.  Для  опрацювання  окремих  дій  при  розв’язуванні  задач використовуються картки з друкованою основою, які містять певні наочні  опори.  Наприклад,  опрацьовуючи  дію  складання  короткого  запису  задач,  діти  розв’язують  задачі  на  картках  з  друкованою основою, на яких вже є ключові слова і треба записати відповідні ним числа.  До  засобів  навчання  можна  також  віднести  опорні  схеми простих  і  складених  задач,  що  подані  на  окремих  картках; також опорні схеми «типових» задач та узагальнені плани їх розв’язування тощо.

 

 

 

 

 

 

 

 

3. Досвід практичного застосування комп’ютерних технологій на уроках математики

Впровадження новітніх інформаційних технологій стрімко увійшло у повсякденне життя вчителя, вихователя, педагога. Крокуючи в ногу з часом, наше завдання кожного дня самовдосконалюватися, займатися самоосвітою, ділитися досвідом використання ІКТ технологій.

Досвід показує, що комп'ютер сприяє не тільки розвитку самостійності, творчих здібностей учнів, його застосування дозволяє змінити саму технологію надання освітніх послуг, зробити уроки більш наочними і цікавими.

Комп'ютер забезпечує взаємозв'язок учителя та учнів на уроці, сприяє здійсненню диференціації та індивідуалізації навчання, розвитку творчих здібностей та загальної обдарованості учнів, формуванню знань, посилює міжпредметні зв'язки. Все це дає можливість покращити якість навчання.

Процес організації навчання школярів з використанням ІКТ дозволяє:

• зробити цей процес цікавим, з одного боку, за рахунок новизни і незвичності такої форми роботи, а з іншого, зробити його захоплюючим і цікавим, різноманітним за формою за рахунок використання мультимедійних можливостей сучасних комп'ютерів;
• ефективно вирішувати проблему наочності навчання, розширити можливості візуалізації навчального матеріалу, роблячи його більш зрозумілим і доступним для учнів;
• індивідуалізувати процес навчання за рахунок наявності різнорівневих завдань, тестових програм;
• здійснювати самостійну навчально-дослідну діяльність (моделювання, метод проектів, розробка презентацій, публікацій тощо), розвиваючи тим самим у школярів творчу активність [7, с.2].

Інформаційні технології, на наш погляд, можна використовувати на різних етапах уроку: на етапі актуалізації знань учнів з даної теми, при введенні нового матеріалу, при формуванні вмінь та навичок, доцільно використовувати на етапі закріплення матеріалу, перевірки та контролю знань, а також у домашніх завданнях і позакласній роботі.

Які саме ІКТ технології використовувати кожен учитель обирає самостійно. На це впливає багато факторів. А саме, наявність комп'ютерного та мультимедійного забезпечення, грамотне володіння учнями основ роботи з ПК, наявність вільного доступу до мережі Інтернет тощо.

Комп'ютерне забезпечення уроків математики потребує належного прикладного програмного забезпечення (ППЗ). Вибір програм та розробка дидактичних комп'ютерних засобів здійснюється вчителем на основі наступних принципів:

• Доступність. У цьому принципі сконцентровані такі ідеї, як вибір ППЗ, що вже є у наявності (програми, що вже є у наявності на комп'ютері), а також підбір програм, з якими ознайомлений вчитель і вміє з ними працювати.
• Простота. Тут мається на увазі можливість учнів працювати з деякими програмами (текстовим та графічним редактором, тестовими програмами).
• Надійність. Програми, які використовує вчитель, мають бути ліцензовані, щоб не принести випадкової шкоди психічному чи фізичному здоров'ю дітей, які з ними працюють.
• Практична багатофункціональність. Можливість вчителя донести в цій програмі якомога більше корисної інформації для учнів: підібрати або створити малюнки, таблиці, схеми або іншу наочність, роздрукувати її, використовувати як наочний посібник саму програму або її продукти тощо [8, с.З].

Учні на уроках математики аналізують умову задачі. Потім вирішують її. Однак схоже завдання на «контрольної» багато учнів класу не можуть вирішити. І це зрозуміло: на уроці вони орієнтувалися на вказівки вчителя, а самостійно організувати свої дії навчаються не можуть. Причому, якщо при традиційному навчанні вчитель має можливість судити про правильність роботи кожного з учнів у класі головним чином за кінцевим результатом, після того, як роботи учнів зібрані і перевірені. То при використанні комп'ютерних технологій вчитель має можливість проконтролювати кожен крок роботи кожного з учнів у класі.

Наприклад, при роботі з програмою «Репетитор з математики» (Кирило і Мефодій) можна в режимі «Тренінгу» і «Завдання» створювати «закладки», розбивши всі наявні питання та завдання на теми, необхідні вчителю на даному уроці, на даному етапі вивчення теми і для кожного учня окремо, що є великою перевагою цієї програми. Ця програма розрахована на індивідуальні особливості учнів, забезпечує можливість працювати в індивідуальному темпі кожному учневі. Самостійність і активність учнів сприяє можливості самоврядування навчальною роботою на екрані. Учитель може моделювати завдання математики для «слабкого» і «сильного» учня в ході самостійної роботи, розділивши завдання на варіанти різні за складністю.

Інформаційні технології дозволяють дати учням унікальну можливість самим в процесі незалежно від вчителя дізнатися нове поняття, підмітити закономірність, висунути власну гіпотезу, відчути, як виникають математичні питання.

Комп'ютеризація дозволяє реалізувати навчання розв'язання задач на трьох рівнях:

• перший - для школярів, які не збираються продовжувати свою освіту після закінчення середньої школи
• другий - для тих, хто в майбутньому збирається опанувати гуманітарними спеціальностями;
• третій - для тих, хто планує здобути технічну освіту;
• четвертий, додатковий рівень можна відвести для учнів, які планують зробити математику своєю професією.

 При цьому перехід від одного рівня до іншого здійснюється в рамках однієї програми. Саме евристичні завдання цих програм сприяють певному перерозподілу акцентів у досліджуваному матеріалі, так як вивчається не тільки математичний зміст, а й прийоми, а також способи дій, властиві діяльності творчого характеру.

Використання інформаційно-комунікаційних технологій в процесі навчання підсилює в учнів потребу в здобутті додаткових знань, оскільки створюються умови для:

· індивідуальних навчальних можливостей і потреб;

· широкого вибору змісту, форм, темпів і рівня їх загальноосвітньої підготовки;

· задоволення освітніх потреб в поглибленому вивченні предмета;

· розкритті творчого потенціалу учнів: участь у конкурсах, олімпіадах;

· активного самостійного засвоєння знань.

На уроках математики можливе використання персонального комп'ютера за такими напрямками, як:

· контролююча машина;

· навчальний тренажер;

· моделюючий стенд;

· інформаційно-довідникові системи;

· ігрове навчальне середовище;

· електронний конструктор

· експертна система.

За допомогою комп'ютера легко створити на уроці цікаву ігрову ситуацію. Учні з захопленням відправляються на пошуки піратських скарбів, фантастичних світів, в космічні подорожі, але для цього їм доведеться засвоїти певні математичні знання та отримати необхідні математичні навички.

Комп'ютер може узяти на себе виконання навчальних функцій, не

говорячи вже про функції тренувального характеру, орієнтовані на закріплення знань, умінь, навичок. Вважаю, що систематичне використання

У процесі навчання важлива не інформаційна технологія сама собою, а

те, наскільки її використання сприяє досягненню освітніх цілей. Тому

необхідно також розв’язати психолого-педагогічні проблеми комп’ютерного навчання, а саме:

• уроки у комп’ютерному класі викликають емоційне піднесення в учнів, що не завжди сприяє ефективності процесу навчання. Тому 1-2 уроки протягом семестру носитимуть лише показове навантаження, а не навчальне. Для оптимізації процесу навчання математики необхідне систематичне використання комп’ютерних технологій;
• комп’ютерні уроки вимагають від учнів організованості, швидкості мислення, вміння переключати увагу протягом всього навчального часу.

Комп’ютерна презентація – одна із форм сучасного уроку, яка дозволяє зробити учбовий матеріал яскравим і переконливим.

Мультимедійні сценарії уроків виконуються у вигляді презентацій з використанням програми Microsoft Office Power Point.

Слайди презентацій, зазвичай, містять ілюстративний матеріал для

уроку, фрагменти відеофільмів, анімації. При підготовці презентації заздалегідь продумується структура уроку, послідовність слайдів визначає певний темп і логіку викладення матеріалу, тобто створюється сценарій проведення уроку. На слайдах розміщують короткі тези, дати, імена, терміни, визначення, формули, які необхідно учням запам’ятати.

Найбільш важливий матеріал для підключення асоціативної зорової пам’яті виділяють кольором, шрифтом, обрамленням тощо.

Є багато позитивних моментів при використанні такої методики:

1. Яскраві образи без надмірних зусиль надовго запам’ятовуються.

2. Завдяки рухливості малюнків, схем, таблиць є можливість їх

змінювати, доповнювати, корегувати, заповнювати поетапно, частинами, чи повернутись до попереднього моменту, повторити якийсь епізод.

3. Використання мультимедійних засобів на уроках сприяє створенню позитивної атмосфери, що має велике значення для сприйняття інформації.

Мультимедійні презентації зручно використовувати на уроках при

поясненні нового матеріалу, при повторенні вивченого матеріалу, при

організації поточного контролю знань (презентації-опитування), а також в

позаурочний час при створенні проектів і творчих робіт з математики.

Джерелом ілюстративного матеріалу для презентацій служать:

· СD-диски мультимедійних курсів математики;

· СD-диски електронних енциклопедій;

· Матеріали з Інтернет-джерел ;

· Матеріали, створені власноруч вчителем чи учнями

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Приклади практичного використання комп’ютерних технологій при вивченні сюжетних задач

Розробка конспекту уроку для 1 класу.

Тема. Складання і розв’язування прикладів на додавання і віднімання. Задачі на знаходження суми. Вимірювання довжини відрізків.

Мета:

• закріпити обчислювальні навички в межах 10, склад чисел у межах 10;
• удосконалювати вміння розв’язувати задачі на знаходження суми;
• закріпити вміння вимірювати і креслити відрізки;
• розвивати логічне мислення, кмітливість, спостережливість; виховувати інтерес до математики.

Обладнання: план подорожі, силуетні малюнки казкових героїв, картки для обчислень, лист від героя, презентація, відео фізкультхвилинка.

Тип уроку: урок застосування знань, умінь та навичок.

Форма проведення: урок-подорож.

 

ХІД УРОКУ

І.  Організація класу до уроку

1. Привітання.  

       2. Психологічна установка. Емоційне налаштування на урок.

ІІ. Мотивація навчальної діяльності

•    Діти, сьогодні вам прийшов лист від одного з казкових героїв. Ви його всі добре знаєте. Він добрий, кумедний. Прочитаймо лист. (Діти читають лист)

Дорогі друзі!

Запрошую вас до себе в гості. Дорога важка, але ваші знання

з математики допоможуть подолати всі перешкоди. А

супроводжувати вас буде моя маленька подружка – бешкетниця Маша. Бажаю успіхів.                                                                                           

Ваш ведмедик Мишко.

•    А ось і карта, щоб ми змогли потрапити до його будинку.
•    Дорога  далека, тому щоб подолати всі перешкоди ви повинні використати всі свої  знання з математики:

• повторити таблиці додавання і віднімання,
• навчитися рахувати в межах 20,
• скласти та розв’язати задачі,
• попрацювати з геометричним матеріалом.

•    Ви згодні вирушити в подорож? (Так.)
•    Ми помандруємо на автомобілях. Але перед тим як вирушити в дорогу, давайте перевіримо, чи справний наш транспорт, чи готові ми до подорожі.

ІІІ. Повторення і закріплення вивченого матеріалу

1. Інтерактивна технологія „Мозковий штурм”

2.              Каліграфічна хвилинка
3.              Математичний диктант
4.             
   Гра «Хто швидше» (в парах за партами та біля дошки; індивідуально – порівняти числа.)

Дидактична гра «На яку квіточку впала крапелька»  

 

               1+6        9-2

    10-5           8+1                          4+5            7-2 

 

5.              Робота з підручником

Фізкультхвилинка (музична)

6.              Розв’язування задач

•                  Діти, перед нами проспект Задачний.
  •           Віршовані задачі(презентація)
•                  Чи вмієте ви розв’язувати віршовані задачі.

                  На траві навколо хати

                  Метушились каченята

                  П ять білесеньких, як сніг

                  Двоє чорних,скільки всіх? (5+2=7 – запис в зошити прикладу)

    Біля річки на галявці

    Знайшли моркву сірі зайці

    Вісім морквин це немало.

    Одну з’їли. Скільки стало? (8-1=7 – запис в зошити прикладу)

 Пані Хрюша – господиня,

Добрі виростила дині!

Десять штук, такі смачні!

Ще й чотири кавуни!

На скільки більше динь, скажіть,

Лічити їй допоможіть. (10-4=6 – запис в зошити прикладу)

П’ять метеликів літають

І на квіточки сідають,

Прилетів ось ще один.

Сів на квіточку і він.

Полічимо швидше всіх –

Цих метеликів прудких. (5+1=6 – запис в зошити прикладу)

•            Розв’язування задачі за малюнком

 – Скласти і розв’язати задачу за малюнком (Малюнок в презентації)

    Маша знайшла 5 червоних яблук і 2 зелених. Скільки всього яблук знайшла Маша?

 

 

 

 

 

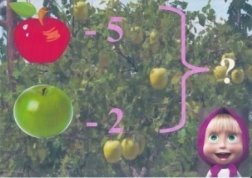
• З яких частин складається задача?
• Повторіть умову, запитання.
• Скільки червоних яблук знайшла Маша? (5)
• Скільки зелених? (2)
• Що позначає число 5, 2?
• Якою дією розв’яжемо задачу ? (+)
• Запишемо приклад – розв’язання у зошити. (5+2=7(ябл.))
• Закрийте очі, погладьте личко, вушка, відкрийте очі. (Заміна малюнка)
• Подивіться уважно на малюнок. Що змінилось? (Умова)

• Складіть задачу і запишіть розв’язання. (Маша знайшла 5 червоних яблук і стільки ж зелених. Скільки всього яблук знайшла Маша?) (5+5=10(ябл.))

2.               Робота з геометричним матеріалом. Вимірювання довжини відрізка.

ІV. Підсумок уроку

        «Мікрофон».

 

 

Розробка конспекту уроку для 3 класу.

Тема:       Засвоєння таблиці множення числа 8. Розв’язання задач на зведення до  одиниці.

Мета:   

• вправляти учнів у застосуванні знань таблиці множення числа 8 під час розв'язання математичних виразів і задач;
• закріплювати знання таблиць множення і ділення чисел від 2 до 8;
• розвивати пам'ять, увагу, логічне мислення;
• сприяти вихованню наполегливості, самостійності, взаємодопомоги.

Обладнання: презентація, Rich Test, карточки для індивідуального опитування.

Тип уроку: закріплення набутих знань.

                                            ХІД УРОКУ

I. Організація класу до уроку.

ІІ. Мотивація навчальної діяльності

III.      Перевірка домашнього завдання.

                 - Подивіться на слайд. Чи так ви розв’язали задачу вдома?

                      - Якщо б у їдальні було 70 кг борошна, відповідь збільшилася? (ні, зменшилася)

                        - А на скільки зменшилася? (На 10 кг)

IV. Математична розминка. Усні обчислення.

Робота з картками.

Хвилинка каліграфії.

V. Повідомлення теми і мети уроку.

- На нашому математичному стадіоні будемо вправлятися в застосуванні знань таблиці множення числа 8 при розв'язанні математичних виразів і задач. А працювати будемо під девізом: «Ні кроку без думки!»

Гімнастика для очей.

VI. Закріплення вивченого матеріалу.

-  Перемога у спорті – це успіх команди, тому так важливо взаєморозуміння та взаємодопомога. Перед зборами відповідальних змагань, у спортсменів перевіряють стан здоров’я. Тому я зараз хочу перевірити ваші знання, чи готові ви працювати на нашому математичному стадіоні?

1 група розв’язує приклади з підручника;

2 група – попрацює на комп’ютері над тестами

Фізкультхвилинка.

- Робота над задачами.

- Щоб спортсмени були вправними, швидкими і вони здобули перемогу, їм під час тренувань ускладнюють завдання.

- Ви готові до складних завдань?

- Складіть задачі за короткими записами та розв’яжіть їх.

- Що є спільного в задачах? ( за 7 матчів забили 42 м’ячі )

- Що є відмінного в задачах? ( в першій задачі – знайти кількість м’ячів; в другій задачі – знайти кількість матчів)

- Діти, як можна назвати ці задачі?  (Ці задачі називають оберненими).

Логічні задачі (резервний матеріал)

VII. Підсумок уроку.

VIII. Домашнє завдання (різнорівневе).

 

 

 

ВИСНОВОК

Головне завдання вчителя зробити навчання цікавим. Тому на урок потрібно йти не лише зі знанням навчального матеріалу, методів і прийомів навчання, набором задач і вмінням їх майстерно розв'язувати, але і з різноманітними та цікавими способами організації роботи учнів. Таке непросте завдання можна вирішити лише шляхом поєднання традиційних методів навчання з використанням інноваційних технологій, серед яких чільне місце займають інформаційно-комунікативні технології навчання.

Вони відкривають нові, ще недостатньо досліджені можливості вдосконалення навчальної діяльності. Позитивний результат гарантовано, бо молодь до комп'ютерів ставиться дуже доброзичливо, вона їх любить, їм довіряє, навіть їх обожнює. І треба розумно використати це ставлення школярів до комп'ютера при плануванні навчального процесу.

Важливі також деякі психологічні аспекти даної теми. Учні мають різний психологічний статус і багато хто з них хворобливо ставиться до

зауважень, дуже боїться зазнати фіаско на очах у класу. У діалозі з комп'ютером нічого подібного не відбувається: комп'ютер не рахує, скільки було невдалих спроб розв'язання задачі, не робить ніяких зауважень. Він ще й підкаже, що і як потрібно зробити. Таким чином формується ситуація психологічного комфорту, яка створює можливість пізнавальної та емоційної свободи учнів.

Використання комп'ютера можливе на всіх етапах, що складають процес навчання: представлення нового матеріалу учням, перевірка засвоєння ними знань, що вивчаються, уточнення змісту матеріалу і методів його викладання, фіксація всіх успіхів і невдач. Бурхливий розвиток електронних оптичних методів зберігання, передачі та обробки інформації призводить до переконання - необхідно на уроках використовувати комп'ютер, це значно підвищує ефективність навчання. Комп'ютерна підтримка уроків може бути надзвичайно різноманітна:

• Відео-та анімаційні фрагменти;
• Матеріали для тестового контролю (підсумкового, рубіжного,

діагностичного);

• Комплекти завдань для самостійної та групової роботи, із зразками
• рішень і можливістю перевірки результатів у комп'ютерному експерименті;
• Анімаційні малюнки, логічні схеми, інтерактивні таблиці тощо, які

використовуються в ході пояснення, закріплення та систематизації

• досліджуваного матеріалу.

Використання на уроках математики елементів такої педагогічної технології забезпечує кожному учневі формування позитивної мотивації до процесу навчання; розвиток мислення, пізнавальної самостійності, інтелектуальних і практичних умінь і навичок; розвиток ІКТ - компетентності учнів; раціональне використання часу на уроці; формування навичок самостійної, групової та колективної роботи учнів.

Досвід роботи показує, що такі уроки викликають в учнів справжній інтерес, примушують працювати всіх, навіть слабших учнів. Якість знань при цьому помітно зростає.

Від освіти сьогодні потрібно більше, ніж вчора. І саме використання на уроках інформаційних технологій допоможе вчителю побудувати навчальний процес більш ефективно, що сприяє формуванню сильної особистості, здатної жити й працювати у світі, що безперервно зазнає змін, здатної сміливо розробляти власну стратегію поведінки, здійснювати моральний вибір і нести за нього відповідальність. Тобто такої особистості, яка спроможна саморозвиватися і само реалізуватися.

Завдання поставлені на початку експерименту, нами були вирішені, мета дослідження досягнута, гіпотеза підтверджена.

 

 

 

 

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Балл Г.А. О психологическом содержании понятия «задача» // Вопросы психологии. 1970. № 6. С.17-22.
2. Бібік Г.В. Досвід інтеграції уроків математики й інформатики // Комп’ютер в школі та сім'ї. - 2004. - № 5. - С. 29-32. 
3. Богданович М.В., Козак М.В., Король Я.А. Методика викладання математики в початкових класах: Навч.посібник. - 2-е вид., перероб. і доп. - Тернопіль: Навчальна книга – Богдан, 2001. - 368 с. 
4. Брушлинский А.В. Психология мышления и проблемное обучение. М., 1983. 96 с.
5. Драч П.М. Заняття з математики з використанням комп'ютерної техніки // БВПШ. - 2003. - № 11. - С. 6-9. 
6. Дятлова С.І. Наочні засоби на уроках математики // Поч. школа. - 1990. № 5. - С. 45-47. 
7. Колягин  Ю.М.  Задачи  в  обучении  математике.  Ч.  I  //  Математические  задачи  как  средство обучения и развития учащихся. М., 1977. 110 с.
8. Король Я.А. Математична скарбничка: Навчальний посібник для дітей 6-7 -річного віку у двох частинах. - Тернопіль: Мандрівець, 1997. 
9.  Крупич В.И. Теоретические основы обучения решению школьников математических задач: дис. д-ра. пед. наук. М., 1992. 395 с.
10. Матюшкин А.М. Мышление, обучение, творчество. М., 2003. 719 с.
11. Мендыгалиева А.К. Система задач как средство развития младших школьников при обучении математике (на примере задач на движение): Дисс. … канд. пед. наук. – С-Пб., 1995. – 134 с.
12. Мізюк В. А. Формування вмінь учнів початкової школи розв'язувати текстові задачі: Автореф. дис... канд. пед. наук — К., 2000.
13. Ожогін В.Я. Технічні засоби в навчальному процесі.  Інформаційні властивості і ергономічні особливості застосування. – К.: Вища школа, 1984. - 194 с. 
14. Пометун О. І. Сучасний урок. Інтерактивні технології навчання : наук.-метод. посібн. / О. І. Пометун, Л. В. Пироженко; заг. ред. О.І. Пометун. К.: А.С.К., 2004.  ̶ 193 с.
15. Пономарев Я.А. Психология творчества. М., 1976, 304 с.
16. Програми середньої загальноосвітньої школи 1-4 (1-3) класи. - К.: Освіта, 1994. - 254 с. 
17. Роберт, И.В. Современные информационные технологии в образовании : дидактические проблемы; перспективы использования / И.В.Роберт. ̶ М. : Школа  ̶  Пресс, 1994.  ̶  205 с.
18.  Свечников А.А. Решение математических задач в 1-3 классах. М., 1976. 160 с.
19. Сергеева, Т. Новые информационные технологии и содержание обучения / Т.Сергеева // Информатика и образование. – 1991.  ̶  № 1.  ̶  С. 3 – 10.
20. Сиротенко, Г.О. Сучасний урок : інтерактивні технології навчання / Г. О. Сиротенко. – Х. : ВГ «Основа», 2003. – 80 с.
21. Скворцова С. О. Методика навчання розв’язування сюжетних задач у початковій школі. Навчально-методичний посібник для студентів. – Ч.І: Методика формування в молодших школярів загального уміння розв’язувати сюжетні задачі / С. О. Скворцова. – Одеса: ООО «Абрикос-Компани», 2011. – 268 с.
22. Скворцова С. О. Методика навчання розв’язування сюжетних задач у початковій школі. Навчально-методичний посібник для студентів. – Ч.ІІ: Методика формування в молодших школярів умінь розв’язувати задачі певних видів / С. О. Скворцова. – Одеса: Фенікс, 2011. – 156 с.
23. Скворцова С. О. Методична система навчання розв’язування сюжетних задач учнів початкових класів: Монографія / С. О. Скворцова. – Одеса: Астропринт, 2006. – 696 с.
24. Скворцова С.О. Методика формування у молодших школярів загальних умінь розв’язувати сюжетні математичні задачі (на матеріалі простих задач) // Матер. Між нар. наук.-практ. конф. „К.Д.Ушинський і сучасність: пріоритетні напрямки розвитку професійної освіти”. 21-22 жовтня 2004. Том 1. – Одеса, 2004. - С.76 - 80
25. Скворцова С.О. Методика формування у молодших школярів загальних умінь розв’язувати сюжетні математичні задачі ( на матеріалі складених задач) // Наука і освіта. -  № 6-7. - 2004. – С.275-277
26. Статкевич В.В. О начальном обучении решению задач. Минск, 1970. 208с.
27. Утепкалиев С. Методика обучения младших школьников самостоятельному решению текстовых задач по матемаике: Дисс… канд. пед. наук – Атырау, 1998. – 176 с.
28. Фридман Л.М. Сюжетные задачи по математике. История, теория, методика. М., 2002. 208 с.
29. Фридман Л.М. Сюжетные задачи по математике.– М.: Школьная Пресса, 2002. – 208 с.
30. Царева С.Е. Обучение решению текстовых задач, ориентированное на формирование учебной деятельности младших школьников. – Новосибирск: Изд-во НГПУ, 1998. – 135 с.