Міністерство освіти і науки України

Державний заклад

«Луганський національний університет імені Тараса Шевченка»

Навчально-науковий інститут публічного управління, адміністрування

та післядипломної освіти

Рибалка Анна Андріївна

ТЕМА: Використання навчальних і контролюючих програм при застосуванні комп’ютерiв для вивчення геометрії в 7-9 класах

Кваліфікаційна робота

за спеціальністю «Середня освіта. (Математика)»

Старобільськ – 2021

Зміст

1. Вступ

2. Програмні засоби навчального призначення

3. Програмні засоби для підтримки вивчення геометрії основної школи

3.1. Програмно-методичний комплекс GRAN

3.2. Програмний засіб DG – пакет динамічної геометрії

3.3. Програма створення тестів Test-W2

4. Висновки

5. Список використаних джерел

1.  Вступ

Сьогодні все більш актуальним в освіті стає питання про застосування та створення нових технічних умов навчання, не лише на уроках інформатики в школі, а й інших дисциплін – алгебри, геометрії, фізики, хімії, біології тощо.

В курсі геометрії існує дуже багато цікавих задач, які дозволяють глибоко пізнавати не тільки саму геометрію, але й математику в цілому. Серед таких задач важливе місце посідають задачі на побудову. Як правило, такі задачі формулюються дуже просто, але потребують багатьох знань для свого розв’язання. Ці задачі спонукають здобувачів освіти шукати необхідні елементи для вирішення питання, вивчати властивості геометричних фігур, більш глибоко засвоювати геометричні твердження. Задачі на побудову залишаються актуальними і потрібними в практичному змісті і сьогодні.

Тому, щоб зацікавити здобувачів освіти у вивчення геометрії як дисципліни, прогресивний вчитель в наш час має можливість за допомогою програмних засобів під час уроку продемонструвати різні геометричні об’єкти та процеси їх побудови, зокрема побудову графіків функцій або геометричних фігур, що вивчаються в шкільному курсі геометрії у 7-9 класах.

Однією з проблем для школярів у вивченні геометрії є те, як підійти до доведення теореми або розв’язку досить абстрактної задачі. А проблема вчителів – як навчити здобувачів освіти знаходити потрібний підхід. Справа в тому, що хоча геометрична, просторова уява притаманна деяким школярам, але таких не так вже й багато. Більшій частині школярів потрібна допомога в розвитку вміння представляти і зображати стандартні планіметричні конфігурації, їх доводиться навчати геометричному баченню: розумінню теорем і умов завдань, сформульованих словесно.

Вирішенню цієї проблеми сприяє впровадження в навчальний процес нових навчальних і контролюючих програм при застосуванні комп’ютерів для вивчення геометрії в 7-9 класах, які є ефективним засобом управління пізнавальної діяльності і формуванню просторових уявлень здобувачів освіти. При їх використанні відкриваються величезні можливості, зміни і вдосконалення методики відбору необхідної теоретичної та практичної інформації, яка сприяє поліпшенню формування просторової уяви школярів на уроках геометрії. Такий процес навчання характеризується індивідуальним і диференційованим підходом, призводить до зміни змісту характеру діяльності між учителем і здобувачем освіти.

2.  Програмні засоби навчального призначення

Раціональне використання педагогічних програмних засобів (ППЗ) навчального призначення є невід'ємною складовою сучасного навчання і разом з іншими наочними засобами навчання призводить до поліпшення якості знань здобувачів освіти та підвищення їх інтересу до предмету, який вони вивчають.

Перевагою програмних засобів навчального призначення порівняно з традиційними засобами навчання є наявність зручних у використанні засобів візуалізації навчального матеріалу: статичне та динамічне представлення об'єктів, процесів, явищ, їх складових, наочне представлення закономірностей і результатів проведених експериментів, дослідів, знайдених розв’язків задач.

Навчальні програми подають новий матеріал у вигляді логічно поєднаних блоків і закінчуються набором тестів. Вони сприяють засвоєнню нової інформації та спрямовують процес навчання залежно від рівня знань та індивідуальних здібностей здобувачів освіти.

Тренувальні або програми-тренажери – розраховані на повторення і закріплення вивченого матеріалу.

Імітаційно-моделюючі програми дозволяють вивчати властивості системи на основі моделі. Маніпулюючи доступними для зміни параметрами, здобувач освіти за реакцією системи визначає діапазон допустимих змін і усвідомлює суть процесів, які здійснюються під його керівництвом.

Діагностично-контролюючі програми призначені для діагностування, перевірки й оцінювання знань, умінь і навичок здобувачів освіти.

Бази даних – це джерела інформації з різних галузей знань, у яких за допомогою питань відшукують необхідні відповіді.

Інструментальні програми дають можливість школярам самостійно розв’язувати задачі за короткий час із меншими зусиллями. Вони звільняють від рутинної обчислювальної та статистичної роботи, надаючи здобувачу освіти свободу у виборі методів розв’язання конкретних задач і простір для творчості.

Інтегровані навчальні програми поєднують в собі ознаки двох або трьох перерахованих вище категорій.

Використання навчальних і контролюючих програм при застосуванні комп’ютерів для вивчення геометрії на уроках в 7-9 класах, дозволяє підвищити зацікавленість, а значить і увагу школярів за рахунок новизни способу викладу матеріалу. Підвищується інтерес до навчання і до геометрії в цілому. Здобувачі освіти активно включаються в пошук і підготовку матеріалів до уроків, що в свою чергу розвиває у них навички навчально-дослідницької діяльності і дозволяє домогтися кращих результатів не тільки у вивченні геометрії, а й в інформатиці та інформаційних технологіях. Сучасний етап розвитку шкільної освіти вимагає застосування інформаційних технологій, а саме навчальних і контролюючих програм. Потужні навчальні середовища, навчальні програми, зокрема, по геометрії, є тим засобом, який здатний підвищити якість навчання, зробивши сам процес більш наочним і інтерактивним.

3.  Програмні засоби для підтримки вивчення геометрії основної школи

Інформатизація суспільства, зокрема розвиток засобів комп’ютерної графіки дуже плідно впливає на розвиток геометрії, особливо її алгоритмічних аспектів. Іншими словами, досягнення в геометрії стимулюють розвиток інформатики, яка, в свою чергу, ставить перед геометрією все нові завдання. Цікавим є те, що досягнення комп’ютерної графіки дозволяють створювати нові програми, які можна плідно використовувати для розвитку самої геометрії.

Це, перш за все програми, які дозволяють будувати геометричні моделі досліджуваних об’єктів, маніпулювати ними (тобто інтерактивно змінювати їх параметри), спостерігати за динамікою змін параметрів цих моделей. Такі пакети прийнято називати пакетами динамічної геометрії.

Зокрема гідне місце серед інших займають GRAN 1, GRAN 2D, DG, які дають можливість створювати зображення основних планіметричних або стереометричних фігур, їх комбінацій, здійснювати їх перетворення на координатній площині, проводити комп’ютерні експерименти з математичними моделями.

Названі програмні засоби прості у використанні, оснащені досить зручним і “люб’язним” інтерфейсом, максимально наближеним до інтерфейсу найбільш поширених програм загального призначення (систем опрацювання текстів, управління базами даних, електронних таблиць, графічних і музичних редакторів і ін.), контекстно-чутливою допомогою. Від користувача не вимагається значний обсяг спеціальних знань з інформатики, основ обчислювальної техніки, програмування тощо, за винятком найпростіших понять, цілком доступних для школярів середніх класів.

Використання подібних програм дає можливість здобувачеві освіти розв’язувати окремі задачі, не знаючи відповідного аналітичного апарату, методів і формул, правил перетворення виразів тощо. Наприклад, здобувач освіти може розв’язувати рівняння і нерівності та їх системи, не знаючи формул для відшукання коренів, методу виключення змінних, методу інтервалів тощо, обчислювати похідні та інтеграли, не пам’ятаючи їх таблиць, досліджувати функції, не знаючи алгоритмів їх дослідження, відшукувати оптимальні розв’язки найпростіших задач лінійного і нелінійного програмування, не використовуючи симплекс-метод, градієнтні методи і т.д. Разом з тим, завдяки можливостям графічного супроводу комп’ютерного розв’язування задачі, здобувач освіти чітко і легко буде розв’язувати досить складні задачі, впевнено володіти відповідною системою понять і правил. Використання програмних засобів зазначеного типу дає можливість у багатьох випадках зробити розв’язування задачі настільки ж доступним, як просте розглядання рисунків чи графічних зображень. Відповідні програмні засоби перетворюють окремі розділи і методи математики в “математику для всіх”, що стають доступними, зрозумілими, легкими і зручними для використання, а той, хто розв’язує задачу, стає користувачем математичних методів, можливо не володіючи їх побудовою і обґрунтуванням, аналогічно до того, як він використовує інші комп’ютерні програми (текстові, графічні, музичні редактори, електронні таблиці, бази даних, операційні системи, експертні системи), не знаючи, як і за якими принципами вони побудовані, якими мовами програмування описані, які теоретичні положення покладено в їх основу.

3.1.  Програмно-методичний комплекс GRAN

Програмно-методичний комплекс GRAN створений авторським колективом під керівництвом доктора педагогічних наук, професора, завідувача кафедри інформатики Національного педагогічного університету імені М.П. Драгоманова М.І. Жалдака, академіка, доктора математичних наук.

За допомогою GRAN1 (Graphic Analysis 1) школярі можуть будувати і аналізувати функціональні залежності явного і неявного виду, які задані в декартових координатах, таблично; графічно розв’язувати рівняння, нерівності та їх системи з однією або двома змінними; наближено визначати корені многочленів; досліджувати числові послідовності та функції; обробляти статистичні дані; будувати графіки функції розподілу; обчислювати визначені інтеграли; площі криволінійних трапецій; площі поверхонь і об’єми тіл обертання і т. д. GRAN1 простий у використанні, має «люб’язний» інтерфейс (Рис.1.1).

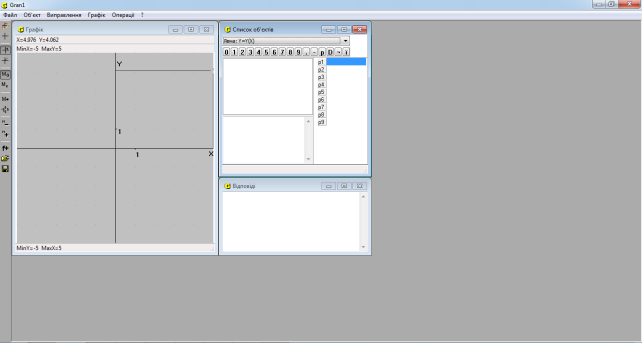
Рис. 1.1. Програмний засіб GRAN 1

Розглянемо розв’язок задачі геометричного змісту за допомогою програмного засобу GRAN 1.

Задача. Дано сторони трикутника: AB = 7,2, BC = 11,2, AC = 9,85. Обчислити міри його кутів (у радіанах).

Для розв’язання даної задачі потрібно виконати таку послідовність дій:

1. Запустити програму GRAN1.
2. Виконати Операції  Калькулятор.
3. Обчислити значення косинуса кута A за формулою 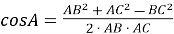, увівши в поле Вираз таку послідовність символів (7.2^2+9.85^2-11.2^2)/(2*7.2*9.85) (рис. 1.2).

Результат обчислень: 0,1651

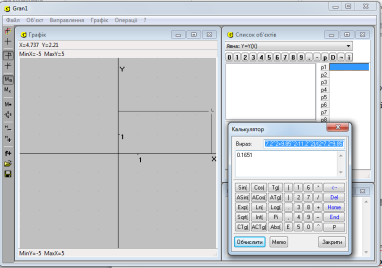
Рис. 1.2. Вікно програми GRAN1: знаходження значення косинуса кута A

4. Обчислити міру кута А (в радіанах) за формулою А=arccos (cos (A)) , увівши в поле Вираз таку послідовність символів AСos(0.1651).(Рис 1.3)

Результат обчислень: 1,405.

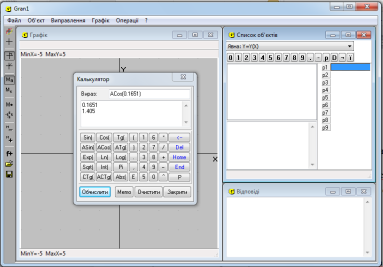
Рис. 1.3. Вікно програми GRAN1: знаходження значення косинуса кута A в радіанах

5. Обчислити значення синуса кута B за формулою: 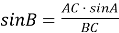, увівши в поле Вираз таку послідовність символів 9.85* Sin(1.405)/11.2. (Рис. 1.4)

Результат обчислень: 0.8674.

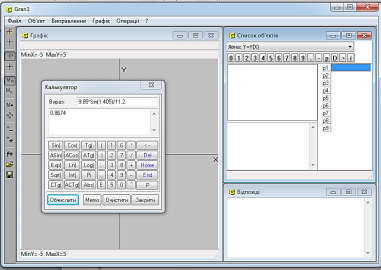
Рис. 1.4. Вікно програми GRAN1: знаходження значення синуса кута B

6. Обчислити міру кута B (в радіанах) за формулою В = arcsin (sin(B)) , увівши в поле Вираз таку послідовність символів ASin(0.8674). (Рис. 1.5)

Результат обчислень: 1.05.

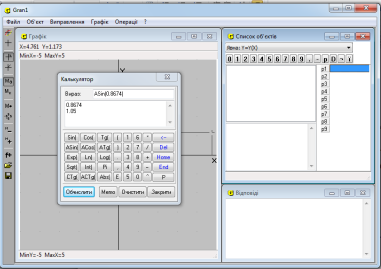
Рис. 1.5. Вікно програми GRAN1: знаходження значення синуса кута В в радіанах

7. Обчислити міру кута С (в радіанах) за формулою C = π – A – B, увівши у поле Вираз таку послідовність символів Pi – 1.405 – 1.05. (Рис. 1.6)

Результат обчислень: C=0.687.

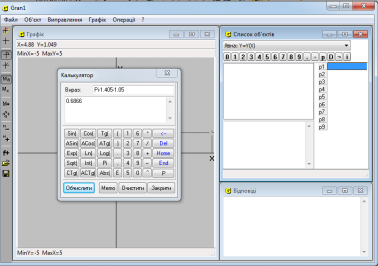
Рис. 1.6. Вікно програми GRAN1: знаходження значення кута С в радіанах

За допомогою засобів динамічної геометрії GRAN 2D зручно вирішувати завдання на побудову на площині, спростовувати окремі припущення. Створивши динамічні моделі, аналізуючи динамічні вирази, можна проводити дослідження геометричних місць точок, встановлювати екстремальні значення певних величин; шукати закономірності, послідовність яких може привести до доказу теорем тощо. Це програмний засіб призначений для графічного аналізу систем геометричних об’єктів на площині, звідки й походить назва (GraphicAnalysis2-Dimension) (Рис.1.7).

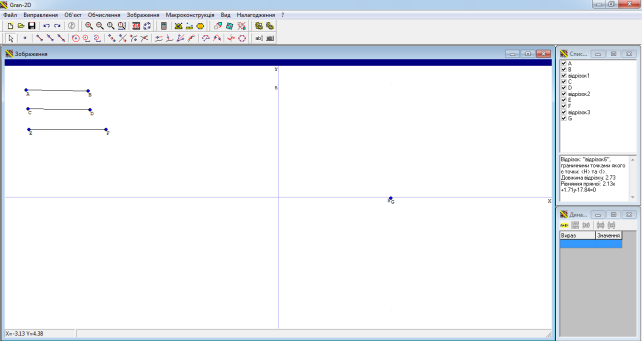
Рис. 1.7. Програмний засіб GRAN 2D

Приклад 1. Побудувати трикутник за трьома заданими сторонами.

Будуємо пряму l, т.G ∈ l, потім будуємо точку H: коло(G;r=EF) ⋂ l=H, далі будуємо точку K: коло(H;r=CD) ⋂ коло(G;r=AB) =K. З'єднуємо ці три точки, так в нас утворюється трикутник GHK за трьома заданими сторонами.(Рис.1.8)

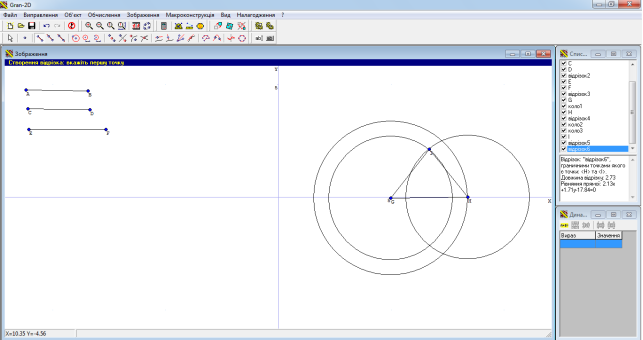
Рис. 1.8. Побудова трикутника в GRAN 2D

Таким чином, програми Gran-1d та Gran-2d можуть бути запроваджені в

навчальний процес до використання під час вивчення таких тем, як побудова графіків функцій та для розв’язку геометричних задач.

3.2.  Програмний засіб DG – пакет динамічної геометрії

Пакет динамічної геометрії DG створений авторським колективом співробітників ХДПУ ім. Г.С. Сковороди для комп’ютерної підтримки шкільного курсу планіметрії. Пакет забезпечує підтримку конструктивного напрямку в навчанні та принципу наочності, надаючи середовище для експериментування. DG – це інтерактивне середовище для експериментування в геометрії.

DG призначений для використання вчителями математики і учнями 7-9 класів на уроках геометрії в школі. Мета пакета – дати учням можливість самостійного відкриття геометрії шляхом експериментування на комп’ютері. DG можна застосовувати для ілюстрування задачі теорем курсу планіметрії, створення і використання наочних інтерактивних навчальних матеріалів. Пакет може також використовуватися і в дослідженнях для створення ілюстрацій, моделювання, формування гіпотез і перевірки їх на правдоподібність. Його можуть з успіхом застосовувати студенти математичних спеціальностей і взагалі всі, хто цікавиться дивовижним світом геометрії.

Основна ідея DG – дати користувачеві можливість робити на комп’ютері побудови, аналогічні класичним геометричним побудовам «на папері». Однак потім DG дозволяє «оживити» отриманий малюнок, поспостерігати, як він «на льоту» змінюється при переміщенні базових точок мишкою. Процес побудови здійснюється за допомогою геометричних інструментів (Рис. 2.1).

Рис. 2.1. Програмне середовище динамічної геометрії DG

Таким чином з’являється можливість створити побудову будь-якої складності за допомогою обмеженого набору основних інструментів. Після завершення побудови можна переміщати вихідні точки мишкою, і все креслення буде динамічно змінюватися, зберігаючи залежності між частинами побудови. Це основний принцип динамічної геометрії. Так DG забезпечує інтерактивність роботи з малюнком і можливість його дослідження в динаміці. Можливості динамічної геометрії – моделювання геометричних побудов; створення побудов за допомогою комп’ютерних аналогів циркуля і лінійки, дослідження отриманих результатів, проведення вимірювань.

Переваги динамічної геометрії:

•              миттєва зміна всіх залежних побудов і вимірювань при зміні деяких вихідних параметрів;
•              створення живих і наочних ілюстрацій, інтерактивних і динамічних навчальних посібників, довідників і експертних систем, використання коментарів, кнопок, підказок і гіперпосилань;
•              організація комп’ютерних експериментів і досліджень, висування і візуальна перевірка гіпотез.

Використання динамічної геометрії DG підвищує ступінь емоційної залученості учнів в заняттях математикою, забезпечує можливість постановки творчих завдань і організації проектної роботи. Демонструє, як сучасні технології ефективно застосовуються для моделювання і візуалізації математичних понять.

Системи динамічної геометрії – це програмне забезпечення, створене для підтримки освітньої та дослідницької діяльності в області геометрії, що дозволяє створювати віртуальні динамічні моделі геометричних об’єктів (динамічні креслення), тобто виконувати побудови геометричного об’єкта на комп’ютері таким чином, що при зміні одного з елементів креслення інші також змінюються, зберігаючи задані алгоритмом побудови співвідношення незмінними.

Розглянемо використання динамічної геометрії DG під час вивчення теми «Взаємне розміщення прямих на площині». (Рис. 2.2)

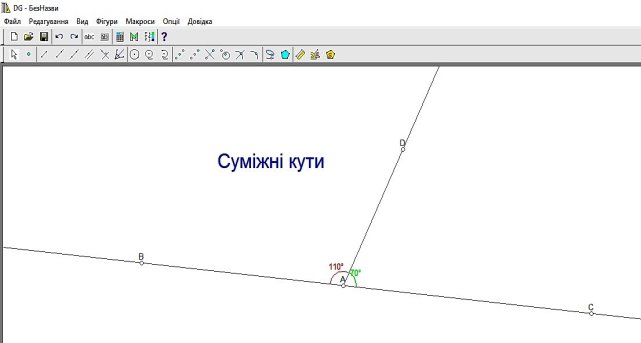
Рис. 2.2 Суміжні кути та їх властивості

При вивченні теми «Взаємне розміщення прямих на площині» на початку уроку «Суміжні кути та їх властивості» можна запропонувати учням побудувати пряму, на ній поставити точку (наприклад т. А) і із цієї точки провести промінь. На основі побудови учням ставляться запитання:

•       Скільки кутів утворилось в одній півплощині? (два)
•       Що вони мають спільного? (спільна сторона)
•       Як на вашу думку називаються ці кути? (суміжними)

Далі учні на основі виконаного рисунка, а згодом і матеріалу підручника, намагаються сформулювати означення суміжних. Коли учні дали означення, потрібно запропонувати позначити ці кути (тобто поставити точки на прямій і на промені, наприклад: т. В, т. С, т. О) і спитати їх, де на цьому рисунку спільна сторона та доповняльні пів промені і, звичайно ж, суміжні кути. Під час наступної частини уроку, а саме, вивчення властивості суміжних кутів, роботу класу можна спрямувати на вирішення навчальної проблеми за допомогою DG - встановити зв'язок між градусними мірами суміжних кутів.

Це можна зробити за допомогою «мозкового штурму»: поділити клас на пари і запропонувати їм проблемне завдання: «Знайти суму величин суміжних кутів»

Учні використовуючи раніше побудовані суміжні кути за допомогою інструменту вимірювання кутів, пакету DG, встановлюють, що сума величин суміжних кутів дорівнює 180°.

3.3.  Програма створення тестів Test-W2

Програми створення тестів ADTester і Test-W2 та проведення тестування на уроках доцільно використовувати:

•              на початку вивчення теми, для самоконтролю: учні шукають у конспектах або підручнику правильні відповіді на тестові запитання;
•              для проведення самостійної роботи: у тестах запропоновано приклади та задачі, які учні розв’язують у зошитах і вибирають правильну відповідь;
•              у кінці вивчення теми для контролю теоретичних знань учнів (при цьому учень не має права підглядати у зошит, книжку чи інший посібник);
•              для самостійного створення сильними учнями тестів до уроків з конкретних тем у позаурочний час.

TEST-W2 – контрольно-діагностична система. Ця система призначена для контролю знань учнів, перевірки відповідності знань вимогам навчальних програм, виявлення рівня навчальних досягнень учнів з будь-якого предмета за допомогою комп’ютера.

До складу системи входять:

•              Test-W2.exe – тестуюча програма;
•              Editor.exe – редактор тестів;
•              Converter.exe – конвертор тестів Test-W у формат Test-W2;
•              Result.dat – протокол результатів тестування (створюється автоматично тільки для читання).

Система Test-W2 надає такі можливості:

•              встановлення індивідуальних параметрів тестування (кількість запитань, час тестування тощо);
•              використання шкали оцінювання на 2, 5, 6, 9 або 12 балів;
•              проведення тестування з діагностикою (в процесі тестування позначаються правильні й неправильні відповіді);
•              авторизація учня (вводиться прізвище, ім’я, клас) та збереження даних у протоколі;
•              захист тестів і протоколу тестування від несанкціонованих дій;
•              редагування тестів;
•              використання можливостей редактора Paint та процесора Microsoft Word для редагування тестів;
•              конвертування тестів системи Test-W2;
•              робота в локальній комп’ютерній мережі.

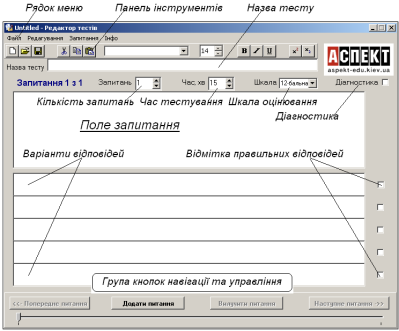
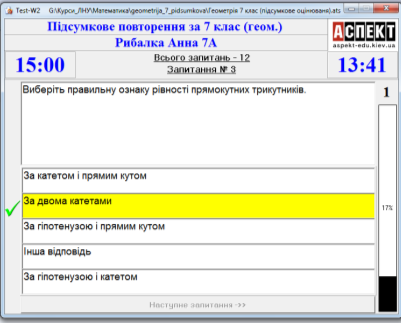
Рис. 3.1. Контрольно-діагностична система Test-W2

4.  Висновки

На уроках геометрії заявлена проблема, яка стоїть в задачі, якоюсь мірою, може бути вирішена шляхом використання комп’ютерних програмних засобів, які, по–перше, мають у своїй основі строгий алгоритм дій здобувача освіти. Адже не кожен здобувач освіти, вивчивши правила, може ними користуватися в практичній діяльності. Використання певних алгоритмів, схем-карт, таблиць, тобто орієнтувальних схем, впорядковує процес навчання і застосування набутих знань.

По–друге, у зв’язку з гострою проблемою економії часу і великим обсягом матеріалу в ході навчального процесу перед сучасною школою також ставиться завдання – знайти такі засоби і прийоми навчання, що дозволяють максимально економити час та засвоювати геометричний матеріал  на уроці. І саме використання інформаційно-комунікаційних технологій на уроках геометрії і є одним з таких засобів.

По–третє, навчання з використанням інформаційно-комунікаційних технологій, а саме програмних засобів – це є рівнева диференціація, тому що в умовах цієї технології здобувач освіти має право на вибір змісту своєї освіти, рівня засвоєння знань і вмінь. При цьому діяльність вчителя повинна забезпечити можливість кожному здобувачу освіти опанувати знання на обов’язковому або більш високому рівні (за вибором здобувача освіти).

У відповідності з поставленими цілями, використання навчальних і контролюючих програм при застосуванні комп’ютерів для вивчення геометрії в 7-9 класах (GRAN 2D,DG, Test-W2 ) повинні допомогти здобувачам освіти отримати більш якісні знання, які необхідні для успішної здачі ДПА.

Крім цього, в якості очікуваних результатів від використання навчальних і контролюючих програм, можна виділити наступні:

•              формування ключових компетентностей здобувачів освіти у процесі навчання і в позаурочній діяльності;
•              підвищення мотивації до навчання здобувачів освіти;
•              оволодіння комп’ютерною грамотністю здобувачами освіти, підвищення рівня комп’ютерної грамотності у вчителя;
•              організація самостійної та дослідницької діяльності здобувачів освіти;
•              створення власного банку навчальних і методичних матеріалів, готових до використання на уроках;
•              розвиток просторового мислення, пізнавальних здібностей здобувачів освіти;
•              естетична привабливість уроків геометрії.

Застосування навчальних і контролюючих програм при вивченні геометрії в 7-9 класах на уроках і в позаурочній діяльності розширює можливості творчості як вчителя, так і здобувачів освіти, підвищує інтерес до предмета, стимулює освоєння здобувачам освіти досить серйозних тем з геометрії, що веде до інтенсифікації процесу навчання.

Отже, застосування комп’ютерних програмних засобів дає змогу вирішити проблему більш якісного засвоєння знань з геометрії в 7-9 класах та здатності їх застосування на практиці, підвищує математичну грамотність здобувачів освіти, сприяє розвитку в них математичної компетентності.

5.  Список використаних джерел

1.               https://studfile.net/preview/9724757/page:3/
2.               https://zhaldak.fi.npu.edu.ua/prohramnyi-zasib-gran
3.               Богач О. В. Застосування інформаційних технологій під час навчання геометрії учнів основної школи. Посібник для вчителів математики. – В., 2020 – 6 с.
4.               Геометрія: підруч. для 7 кл. загальноосвіт. навч. Закладів / А. Г. Мерзляк В. Б. Полонський, М. С. Якір. – Ч. : Гімназія, 2015. – 224 с. : іл..
5.               Державний стандарт базової і повної загальної середньої освіти. /К.: Постанова Кабінету Міністрів України № 804 від 07.06.2017.
6.               Жалдак М. І., Вітюк О. В. Комп’ютер на уроках геометрії: Посібник для вчителів. – К.: РННЦ „ДІНІТ”, 2004. – 168 с.
7.               Раков С. А. Вивчення геометрії на основі дослідницького підходу з використанням пакета динамічної геометрії DG //Математика в школі. – 2005. – No7. – с. 2 – 9.