Властивості функцій для підготовки до ЗНО

 

Варіант 1

 

Частина перша

 

1.1. Графіку якої з наведених функцій належить точка А(8;2)?

А);   Б); В) у=х³;  Г) у=log₂ x.

1.2. Функція у=f(x) парною. Знайти f(4), якщо f(4) = 6.

А) 0;  Б) 6;  В) 6;  Г) знайти неможливо.

1.3. Яка область визначення функції ?

А) (∞;3];  Б) [3; ∞); В) (3;∞);  Г) (∞;3).

1.4. Графік функції у=2^х перенесли паралельно на 3 одиниці вправо вздовж осі абсцис і на 4 одиниці вгору вздовж осі ординат. Графік якої функції було отримано?

А) у=2^х–3 – 4; Б) у=2^х–3 + 4; В) у=2^х+3 + 4; Г) у=2^х+3 – 4.

1.5.  Якого найбільшого значення може набувати функція f(х)=3сos4х1?

А) 11; Б) 2;  В) 4;   Г) 1.

1.6. Яка з функцій зростає на проміжку (0;∞)?

  А);  Б) y = 8x; В) y = 8^x; Г) y = log₈ x.

1.7. У якій координатній чверті знаходиться вершина параболи у=(х+8)²12?

А) у І чверті;      Б) у ІІ чверті; В) у ІІІ чверті;      Г) у ІV чверті.

1.8. Чому дорівнює значення функції в точці х₀=9?

А) 2;   Б) 3;  В) 4 ;   Г) 2.

 

Частина друга

 

2.1. Установити відповідність між функціями (1–4) та їх областями визначення (А–Д):

1.       А (6;+)

2.      Б (–;–2)(–2;2)(2;+)

3.       В (–;6)(6;+)

4.       Г (–;–2(2;+)

        Д [5;+)

 

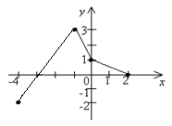2.2. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–4;2], та проміжками (А–Д):

1. функція f(x) зростає на проміжку  А[–4;–3]

2. функція f(x) спадає на проміжку  Б[–3;2]

3. функція f(x)≤0 на проміжку   В[–4;–1]

4. функція f(x)≥0 на проміжку   Г[–2;3]

        Д[–1;2]

 

Варіант 2

 

Частина перша

 

1.1. Серед наведених функцій вказати парну функцію.

А) у = х cosx;  Б) у = х+ cosx; В) у = х sinx; Г) у = х + sinx.

1.2.Чому дорівнює значення функції у точці х₀ = 81?

А) 9;    Б) 27;   В) 3;   Г) 81.

1.3. Графік функції y=tg x перенесли паралельно на дві одиниці вліво вздовж осі абсцис.

         Графік якої з функцій було отримано?

А) y=tg x+2; Б) y= tg x2; В) y= tg (x2); Г) y= tg (x+2).

1.4. Область визначення якої з функцій складається з однієї точки?

  А) ;   Б) ;  В) ;  Г) .

1.5. Знайти координати точки перетину графіків функцій у=lg x і у=2.

А) (2; 100);   Б) (100; 2);  В) (20; 2);   Г) (10; 2).

1.6. У якій координатній чверті знаходиться вершина параболи у=(х+8)²16?

А) у І чверті;      Б) у ІІ чверті; В) у ІІІ чверті;      Г) у ІV чверті.

1.7. Чому дорівнює найбільше значення функції   f(x) = sin x ctg x + 1?

  А) 0;      Б) 1;            В) 2;      Г) такого значення не існує.

1.8. Яка область визначення функції ?

А) (∞;3];  Б) [3; ∞); В) (3;∞);  Г) (∞;3).

 

 

Частина друга

 

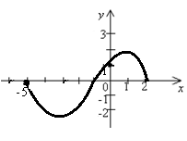2.1. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–5;2], та проміжками (А–Д):

1. функція f(x) спадає на проміжку  А [–5;–3]ᴗ[1;2]

2. функція f(x) зростає  на проміжку  Б [–2;2]

3. функція f(x) ≥0 на проміжку   В [–1;2]

4. функція f(x) ≤ 0 на проміжку   Г [–5;–1]

        Д [–3;1]

 

2.2. Установити відповідність між функціями та їх областями значень:

1.      А

2.      Б [3; 7]

3.     В [1; 5]

4.      Г [–1; 3]

Д [1; 9]

 

 

Варіант 3

 

Частина перша

 

1.1. Графік якої з даних функцій проходить через початок координат?

А) у=sin х;   Б) у=cos х;  В) у=lg х; Г) у=10^х.

1.2.  Якого найбільшого значення може набувати функція f(х)=3сos4х1?

А) 11;  Б) 2;   В) 4;   Г) 1.

1.3. Серед наведених пар функцій вказати пару взаємно-обернених функцій.

А)у=7^х і ;  Б)і ;     В)у=е^х і ;   Г)у=х і у=х.

1.4. Яка область визначення функції ?

А) (0; ∞); Б) (4; ∞); В) (0;4)U(4;∞); Г) (4;5)U(5; ∞).

1.5. Яка з даних функцій спадає на проміжку (0;∞)?

А) у=х²; Б) у=2^х;  В);   Г) .

1.6. Функція у=f(x) парною. Знайти f(4), якщо f(4)=6.

А) 0;        Б) 6;  В) 6;      Г) знайти неможливо.

1.7.Чому дорівнює значення функції у точці х₀ = 16?

А) 2;   Б) 4;   В) 8;   Г) 16.

1.8. Яка область визначення функції ?

А) [3;∞);   Б) (3; ∞); В) [3;∞);  Г) (3;∞).

 

Частина друга

 

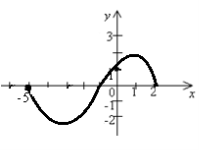2.1. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–5;2], та проміжками (А–Д):

1. функція f(x) зростає на проміжку  А [–5;–3]ᴗ[1;2]

2. функція f(x) спадає  на проміжку  Б [–2;2]

3. функція f(x) ≤0 на проміжку   В [–1;2]

4. функція f(x) ≥0 на проміжку   Г [–5;–1]

        Д [–3;1]

 

2.2. Установити відповідність між функціями (1–4) та їх областями визначення (А–Д):

1.       А (–;+), крім

2. +3      Б [–3;+3]

3.       В (–;–5)(–5;0)(0;+)

4.       Г

        Д (–;+)

 

 

Варіант 4

 

Частина перша

 

1.1.  Вказати область визначення функції .

А) [8;∞);    Б) (8; ∞);  В) [8;∞);  Г) (8;∞).

1.2. Вказати серед даних функцій непарну.

А) у=;  Б) у=;  В) у=;  Г) у=.

1.3. Серед наведених пар функцій вказати пару взаємно-обернених функцій.

А)у=5^х і ;  Б)і ;  В)у=е^х і ; Г)у=х і у=х.

1.4. Як треба перенести паралельно графік функції у=sin x, щоб отримати графік функції ?

А) на одиниць вгору;  В) на одиниць вправо; 

 Б) на одиниць вниз;  Г) на одиниць вліво.

1.5. Яка з наведених функцій зростає на проміжку (0;∞)?

А) у = log_0,4 x; Б) у = ;  В) у = 7х²;  Г) у = .

1.6. У якій координатній чверті знаходиться вершина параболи у=(х4)²2?

А) у І чверті;  Б) у ІІ чверті; В) у ІІІ чверті; Г) у ІV чверті.

1.7. Областю визначення якої з наведених функцій є множина дійсних чисел?

А); Б); В); Г).

1.8.Чому дорівнює значення функції у точці х₀ = 64?

А) 2;    Б) 4;   В) 8;   Г) 16.

 

Частина друга

 

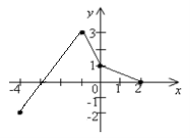2.1. Установити відповідність між властивостями функції f(x) (1–4), зображеної на рисунку графіком на відрізку [–4;2], та проміжками (А–Д):

1. функція f(x) спадає на проміжку  А[–4;–3]

2. функція f(x) зростає на проміжку  Б[–3;2]

3. функція f(x) ≥ 0 на проміжку   В[–4;–1]

4. функція f(x) ≤0 на проміжку   Г[–2;3]

        Д[–1;2]

 

2.2. Задано функцію y=f(x) з множиною значень Установити відповідність між функціями (1–4) та їх множинами значень (А–Д):

1.  y=f(x)+2       А

2. y= –f(x)       Б

3. y=2f(x)      В

4.  y=|f(x)|       Г

   Д