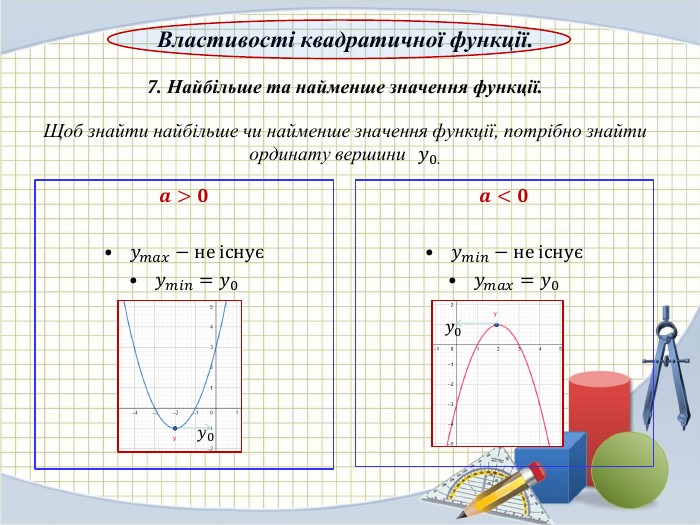
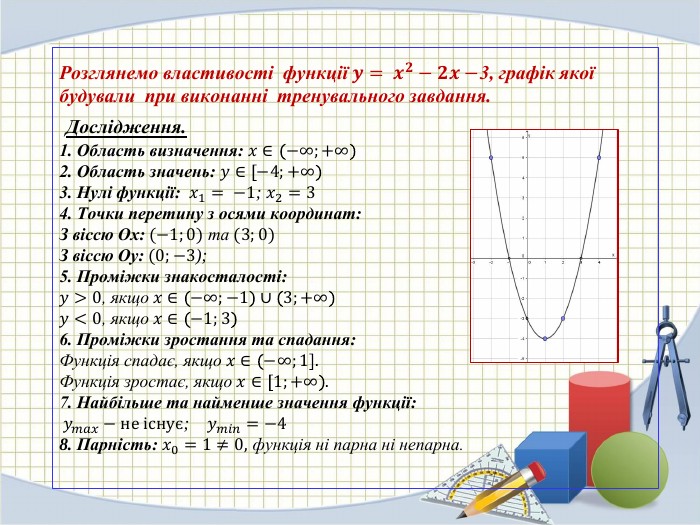
Властивості квадратичної функції.

Властивості квадратичної функціїЗаняття № 4

Вивчаючи тему, ви навчитесь:

Повторення. Квадратичною функцією називають функцію, яку можна задати у вигляді 𝒚=𝒂𝒙𝟐+𝒃𝒙+𝒄, де a,b,c — дійсні числа, a≠0. Графіком квадратичної функції є парабола. Якщо 𝒂>𝟎, то вітки параболи напрямлені вгору. Якщо 𝒂<𝟎, то вітки параболи напрямлені вниз. Координати вершини параболи 𝒚=𝒂𝒙𝟐+𝒃𝒙+𝒄 обчислюються за формулами:𝒙𝟎=−𝒃𝟐𝒂  ;     𝒚𝟎=𝒚 (х𝟎)Точка перетину з віссю ординат: (𝟎;𝒄). Точки перетину з віссю абсцис : (𝒙𝟏;𝟎) і (𝒙𝟐;𝟎), де 𝒙𝟏, 𝒙𝟐 – корені тричлена 𝒂𝒙𝟐+𝒃𝒙+𝒄. Щоб їх знайти потрібно розв'язати рівняння 𝒂𝒙𝟐+𝒃𝒙+𝒄=𝟎. Графік квадратичної функції:може не мати точок перетину з віссю Ox,може мати тільки одну спільну точку з цією віссю,може мати дві такі точки. 

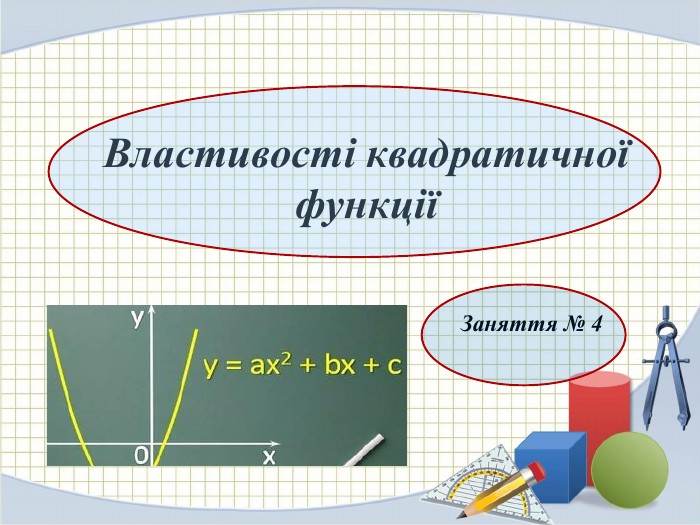
Властивості квадратичної функції.𝒚=𝒂𝒙𝟐+𝒃𝒙+𝒄             𝒂>𝟎 1. Область визначення: 𝒙∈−∞;+∞.2. Область значень: Щоб знайти область значень, потрібно:визначити напрям віток параболи і знайти ординату вершини параболи 𝒚𝟎. 𝒚∈[𝒚в;+∞) 𝒚=𝒂𝒙𝟐+𝒃𝒙+𝒄𝒂<𝟎 1. Область визначення: 𝒙∈−∞;+∞.2. Область значень: Щоб знайти область значень, потрібно:визначити напрям віток параболи ізнайти ординату вершини параболи 𝒚𝟎𝒚∈(−∞;𝒚в] 3. Нулі функціїЩоб знайти нулі функції потрібно розв'язати рівняння𝒂𝒙𝟐+𝒃𝒙+𝒄=𝟎. Якщо D>0, то рівняння має два кореня 𝒙𝟏  і 𝒙𝟐, які будуть нулями функції. Якщо D=0, то рівняння має один корінь 𝒙𝟏, який буде нулем функції, даний корінь буде співпадати 𝒙𝟎. Якщо D<0, то рівняння коренів немає і нулів функції також немає. 

Властивості квадратичної функції.4. Точки перетину з осями координат: з віссю Оу: (0;с)з віссю Ох: немає точок перетину, якщо немає нулів функції(𝒙о;𝟎), якщо є один нуль функції;(𝒙𝟏;𝟎) та (𝒙𝟐;𝟎), якщо є два нулі функції. 

5. Проміжки знакосталості𝒂>𝟎  𝒚>𝟎, якщо 𝒙∈−∞;+∞𝒚>𝟎, якщо х∈−∞;𝒙𝟎∪𝒙𝟎;+∞𝒚>𝟎, якщо  𝒙∈−∞;𝒙𝟏∪𝒙𝟐;+∞ 𝒚<𝟎, якщо 𝒙∈𝒙𝟏;𝒙𝟐  5. Проміжки знакосталості𝒂<𝟎 𝒚<𝟎, якщо 𝒙∈−∞;+∞ 𝒚<𝟎, якщо 𝒙∈−∞;𝒙𝟎∪𝒙𝟎;+∞𝒚<𝟎, якщо 𝒙∈−∞;𝒙𝟏∪𝒙𝟐;+∞ 𝒚>𝟎, якщо 𝒙∈𝒙𝟏;𝒙𝟐  Властивості квадратичної функції.𝒙𝟎 𝒙𝟎 

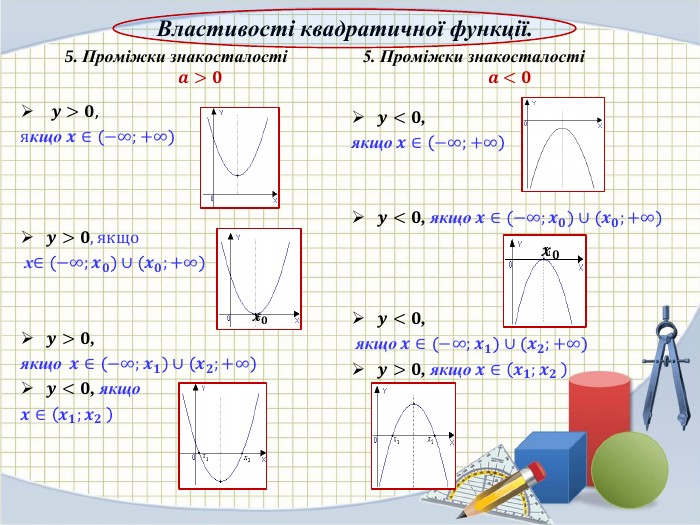
Властивості квадратичної функції.6. Проміжки зростання та спадання. Щоб знайти проміжки зростання та спадання функції , потрібно знайти абсцису вершини параболи 𝑥0=−𝑏2𝑎 . 𝒂>𝟎 Функція спадає при 𝑥∈(−∞;𝑥0]Функція зростає при 𝑥∈[𝑥0;+∞) 𝒂<𝟎 Функція зростає при 𝑥∈(−∞;𝑥0]Функція спадає при 𝑥∈[𝑥0;+∞) 𝑥0 𝑥0 

Властивості квадратичної функції.7. Найбільше та найменше значення функції. Щоб знайти найбільше чи найменше значення функції, потрібно знайти ординату вершини   𝑦0. 𝒂>𝟎𝑦𝑚𝑎𝑥−не існує𝑦𝑚𝑖𝑛=𝑦0 𝒂<𝟎𝑦𝑚𝑖𝑛−не існує𝑦𝑚𝑎𝑥=𝑦0 𝑦0 𝑦0 

Властивості квадратичної функції.8. Парність квадратичної функції. Щоб визначити парність квадратичної функції, потрібно знайти абсцису вершини: якщо вона дорівнює нулю, то функція парна. У решті випадків функція ні парна ні непарна.𝒙𝟎=−𝒃𝟐𝒂=𝟎−парна, 𝒙𝟎=−𝒃𝟐𝒂≠𝟎− ні парна ні непарна 

Розглянемо властивості функції 𝒚= 𝒙𝟐−𝟐𝒙−3, графік якої будували при виконанні тренувального завдання. Дослідження.1. Область визначення: 𝑥∈−∞;+∞2. Область значень: 𝑦∈−4;+∞3. Нулі функції: 𝑥1= −1; 𝑥2=34. Точки перетину з осями координат: З віссю Ох: (−1;0) та (3;0)З віссю Оу: (0;−3);5. Проміжки знакосталості:𝑦>0, якщо 𝑥∈−∞;−1∪3;+∞𝑦<0, якщо 𝑥∈−1;36. Проміжки зростання та спадання: Функція спадає, якщо 𝑥∈−∞;1.   Функція зростає, якщо 𝑥∈1;+∞.7. Найбільше та найменше значення функції: 𝑦𝑚𝑎𝑥−не існує; 𝑦𝑚𝑖𝑛=−48. Парність: 𝑥0=1≠0, функція ні парна ні непарна. 

Дякую за увагу!