Всі уроки по темі "Прості механізми"

Урок 1-2

Тема: Прості механізми.

Мета: Дати уявлення про прості механізми та їх роль у житті людини. Ознайомити з основними елементами простих механізмів.

Обладнання: важіль, блок, коловорот, похила площина, важки, ножиці, кусачки, плоскогубці, таблиці.

 

З давніх-давен людина використовує певні знаряддя праці для виконання роботи: молоток – розбити горіх, забити гвіздок; лопата – перекопати поле; коса – зібрати врожай; сокира – для ваління дерев і тому подібне. Тіло яке застосовують для виконання роботи, перетворення величини сили або її напрямку називають знаряддям (механізмом). Всі механізми можна поділити на два типи найпростіших механізмів: 1) важіль і 2) похила площина.

Важіль - це тверде тіло, що може обертатися навколо нерухомої опори. Кожному відомо, що важкий предмет (камінь, шафу, верстат), який не можна перемістити безпосередньо руками, легко зсунути з місця за допомогою довгої і міцної жердини – важеля. За допомогою важелів три тисячі років тому під час спорудження пірамід у Стародавньому Єгипті пересували й піднімали на велику висоту важкі кам’яні брили.

Демонструємо дію важеля (використовуючи важелі закріплені на магнітній дошці або на штативі). Вказуємо на виграш в силі який дає важіль.

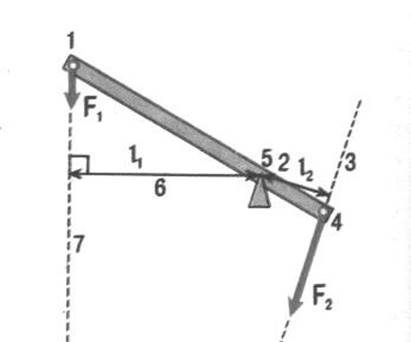Для встановлення правила важеля вводимо такі характеристики. Частини   важеля        до      яких прикладені сили відносно осі обертання називають плечами важеля. Важіль має два плеча (одне плече – частина важеля між точками 1-5, друге плече – частина важеля між точками 24). Точка прикладання сили (1,4) – це точка, в якій на важіль діє сила. Вісь обертання (5) – лінія, перпендикулярна до повздовжньої   осі     важеля. Важіль може вільно обертатися навколо цієї осі. Лінія дії сили (3,7) – це лінія, яка показує напрям дії сили. Найменшу відстань від осі обертання до

напрямку дії сили (довжину перпендикуляра опущеного з осі обертання на напрям дії сили) називають плечем сили. Плечі сил (l₁ і l₂) – визначають, будуючи відрізки, перпендикулярні як до осі обертання, так і до лінії дії сили. Плечі важеля не завжди рівні плечам сил. (Рівність спостерігається за умови прикладання сил перпендикулярно до важеля). Сили прикладені до важеля позначають F₁ i F₂. Плечі сил позначають відповідно l₁ і l₂. Переміщення сил відповідно s₁ i s₂. Швидкості точок прикладання сил v₁ і v₂. Проводячи вимірювання, під час демонстрації піднімання вантажу за допомогою важеля, доводимо правильність наступних співвідношень: F₁/F₂ = l₂/l₁= s₂/s₁ = v₂/v₁; (t₁ = t₂). Важіль дає виграш в силі. В скільки разів плече сили більше в стільки ж разів сила менша. Але при переміщенні шлях меншої сили (прикладеної до довгого плеча) і її швидкість більші в стільки ж разів в скільки дана сила менша.

Існує легенда, що Архімед, захоплений відкриттям правила важеля вигукнув: “Дайте мені точку опори, і я підніму Землю!”. Звичайно Архімед не зміг би здійснити свій намір, якби йому і дали точку опори (яка мала б лежати поза Землею) та важіль потрібної довжини. Піднімаючи Землю всього на 1 см, довге плече важеля описало б дугу величезної довжини. Для переміщення довгого кінця важеля по цьому шляху, наприклад із швидкістю 1 м/с, потрібно було б мільйони    років.          Важелі можна         використовувати двояко. В важелі першого роду        (Мал.1)       –        сили прикладенні        по      різні сторони осі обертання.

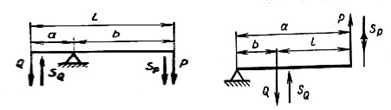
Мал. 1.                              Мал. 2.

В важелі другого роду (Мал. 2)– сили прикладені по одну сторону від осі обертання. Правило рівноваги важеля справджується для обох випадків.

Задача 1. Довжина меншого плеча важеля 5 см, більшого 30 см. На менше плече діє сила 12 Н. Яку силу потрібно прикласти до більшого плеча щоб зрівноважити важіль?

F₁= 12 Н         l₁ = 5см = 0,05 м;     l₂ = 30cм = 0,3 м;  l₁ = 5см            F₁/F₂ = l₂/l₁;       12/F₂= 0,3/0,05;      F₂= 12/6 = 2 (H). l₂ = 30cм F₂ - ?   

Задача 2. На менше плече важеля діє сила 300 Н, на більше 20 Н.

Довжина меншого плеча 5 см. Визначити довжину більшого плеча.

F₁= 300 H         l₁ = 5см = 0,05 м;   F₁/F₂ = l₂/l₁;  300/20 = l₂/0,05; F₂= 20 H            l₂= 15·0,05 = 0,75 (м).

l₁ = 5 см l₂ - ?

Задача 3. На кінці важеля діють сили 40 Н і 240 Н, відстань від точки опори до меншої сили 6 см. Визначити довжину важеля, якщо він перебуває в рівновазі.

F₁= 40 H         l₁= 6 см = 0,06 м;        F₁/F₂ = l₂/l₁;  40/240 = l₂/0,06; F₂= 240 H           l₂= 0,06/6 = 0,01 (м);       l = l₁ + l₂; l₁= 6 см           l = 0,06 + 0,01 = 0,07 (м). l  - ?

Правило важеля лежить в основі дії різноманітних інструментів і пристроїв що застосовуються в техніці й побуті там, де потрібний виграш в силі, або виграш в шляху. Виграш в силі маємо працюючи з таким знайомим всім механізмом як ножиці. Ножиці – це важіль, вісь обертання, якого проходить через гвинт, що з’єднує обидві половини ножиць. Залежно від призначення ножиці бувають різні за будовою. (Демонструються різні типи ножиць). Конторські ножиці, призначені для різання паперу, мають довгі леза і майже такої самої довжини ручки, бо для різання паперу не потрібна велика сила, а довгим лезом зручніше різати по прямій лінії. Ножиці для різання листового металу мають ручки значно довші від лез, оскільки сила опору металу велика і для її зрівноваження плече діючої сили доводиться значно збільшувати. Ще більша різниця між довжиною ручок і відстанню різальної частини від осі в гострозубцях (кусачках), призначених для “перекушування” дроту.

Різного роду важелі є в багатьох машинах. Ручка швейної машинки, педалі і ручне гальмо велосипеда, педалі автомобіля і трактора, клавіші друкарської машини і піаніно – все це приклади важелів. Рукоятки лещат і верстатів, важіль свердлильного верстата – це теж приклади важелів.

На принципі важеля ґрунтується дія і важільних терезів. Навчальні терези діють як рівноплечий важіль (маса вантажу дорівнює масі важків). У десяткових терезах плече, до якого підвішена шалька з гирями, у десять разів довше від плеча, яке несе вантаж. Зважуючи вантаж на десяткових терезах, треба помножити масу гир на десять.

В скелеті тварин і людини всі кістки, які мають деяку рухливість є важелями. Наприклад, у людини – кістки кінцівок, нижня щелепа, череп (точка опори перший хребець), фаланги пальців. У кішок важелями є рухомі кігті, у багатьох риб – шипи спинного плавника, у членистоногих більшість сегментів їх зовнішнього скелета, у двостворкових молюсків – створи раковини, клешні в рака.

Важільні механізми скелета здебільше розраховані на виграш в швидкості при втраті в силі. Особливо великий виграш в швидкості отримується в комах (для швидкого руху крил).

Співвідношення довжин плеч важільного елемента скелета знаходиться в прямій залежності від життєвих функцій які виконує даний орган. Наприклад, довгі ноги гончої і оленя визначають їх здатність до швидкого бігу, короткі ноги крота розраховані на розвивання великої сили при малій швидкості, довгі челюсті гончої дозволяють швидко схопити здобич під час бігу, а короткі челюсті бульдога змикаються повільно, але сильно тримають (жувальний м’яз прикріплений дуже близько до ікол, і сила м’язів передається на ікла майже без послаблення).

В рослинах важільні елементи зустрічаються не так часто, що пояснюється їх малою рухливістю. Типовий важіль – ствол дерева і його продовження головний корінь.

Цікаві важільні механізми можна знайти в деяких квітах (наприклад тичинки шалфея), а також в деяких плодах, що розкриваються. Витягнута тичинка таких рослин являється довгим плечем важеля. На її кінці знаходиться пильник. Коротке плече ніби оберігає вхід в квітку. Коли комаха заповзає в квітку, вона натискає на коротке плече важеля. Довге плече при цьому пильником вдаряє по спині комахи і залишає на ній пилок. Перелетівши на іншу квітку, комаха цим пилком запилює його.

В природі поширені гнучкі органи, які можуть в широких межах змінювати свою кривизну (хребет, хвіст, пальці, тіло змій і багатьох риб). Їх гнучкість зумовлена або поєднанням великого числа коротких важелів з системою тяг, або поєднанням елементів, порівняно негнучких, з проміжними елементами, які легко піддаються деформації (хобот слона, тіло гусениці і ін.). керування згином в другому випадку досягається системою поздовжніх або косо розміщених тяг.

Зупинимось на ще одному прикладі використання важеля.

Який вантаж ви можете підняти рукою? Припустимо, що десять кілограм. Ви думаєте, що ці 10 кг визначають силу мускулів вашої руки? Помиляєтесь: мускули набагато сильніші! Прослідкуємо за дією, наприклад, так званого двоголового м’язу нашої руки. Він прикріплений поблизу точки опори важеля, яким є кістка передпліччя, а вантаж діє на інший кінець цього живого важеля. Відстань від вантажу до точки опори, тобто до суглобу, майже в вісім раз більша, ніж відстань від кінця м’яза до опори. Значить якщо вантаж складає десять кілограм, то мускул тягне з силою в вісім раз більшою. Розвиваючи силу в вісім раз більшу, ніж наша рука, мускул міг би підняти безпосередньо не десять а вісімдесят кілограм.

Ми можемо без перебільшення сказати, що кожна людина набагато сильніша самої себе, тобто що наші мускули розвивають силу, значно більшу ніж та, яка проявляється в наших діях. //Демонстрація моделі руки//

Чи доцільний такий пристрій? На перший погляд ніби ні, - ми бачимо тут втрату сили, нічим не оплачену. Однак згадаймо, що втрачаючи в силі ми виграємо в переміщенні (швидкості). Тут і відбувається виграш в швидкості: наші руки рухаються в вісім раз швидше, ніж м’язи, що ними керують. Такий метод закріплення мускулів, який ми бачимо в тілі тварин, забезпечує кінцівкам спритність рухів, більш важливий в боротьбі за існування, ніж сила. Ми були б вкрай повільними істотами, якби наші руки і ноги не були побудовані по даному принципі.

Добуток сили на її плече називають моментом сили і позначають буквою М. Ця величина потрібна, щоб встановити умови за яких тіло буде перебувати в рівновазі коли на нього діє декілька сил. Момент сили визначається за формулою: М = F·L; М вимірюють в Н·м, F – сила, виміряна в Н, L – плече сили виміряне в м. Тоді правило важеля можна сформулювати так: важіль перебуває в рівновазі коли сума всіх моментів сил що діють на важіль рівна нулю. Причому момент сили береться з знаком плюс (+), якщо сила повертає тіло за стрілкою годинника, і мінус (-) - якщо проти стрілки годинника.

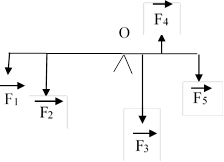Задача 4. На тіло діє п’ять сил, прикладених так як показано на малюнку. Чи перебуватиме важіль в рівновазі, якщо F₁=1 Н, F₂=2 Н, F₃=4 Н, F₄=1 Н, F₅=1,5 Н, L₁=3 м, L₂=2 м, L₃=0,5м, L₄=1 м, L₅=2 м.

Розв’язання.

Запишемо правило моментів:

     - М₁ – М₂ + М₃ – М₄ + М₅ = 0.

М₁= F₁·L₁ =1·3 =3 (Н·м),

М₂= F₂·L₂ =2·2 =4 (Н·м),

М₃= F₃·L₃ =4·0,5 =2,0 (Н·м),

М₄= F₄·L₄ =1·1 =1 (Н·м), М₅= F₅·L₅ =1,5·2 =3 (Н·м). Знайдемо суму всіх моментів: - М₁ – М₂ + М₃ – М₄ + М₅= -3 – 4 + 2 – 1 +3 = -5 (Н·м). Сума моментів не дорівнює нулю. Отже важіль не перебуватиме в рівновазі, а буде повертатися проти годинникової стрілки.

Запитання до учнів.

1.               Чому паличку легше розламати посередині, ніж відламати від неї невелику частину? (При розламуванні палички посередині плечі прикладених сил будуть більші ніж при відламуванні частини. А якщо плече сили більше то сила для розламування буде менша).

2.               Яке призначення ключа під час закручування гайки?

3.               Розламайте сірник пополам, отримані частини знов розламайте пополам і так продовжуйте ламати сірник на все менші шматочки. Чому маленькі шматочки важче розламати ніж великі?

4.               Чому дверну ручку прикріплюють не до середини дверей, а біля їх краю?

5.               Як легше різати ножицями картон: розміщуючи картон ближче до кінців ножиць чи ближче до їх середини?

6.               Як легше перемістити навантажений віз: штовхаючи його в задню стінку чи прикладаючи зусилля до верхньої частини ободу колеса? (Прикладаючи силу до верхньої частини ободу колеса, візник створює вдвічі більший момент сили при однаковому зусиллі. Отже вигідніше прикладати силу саме так).

7.               Чому відкриваючи двері від себе, слід штовхати їх ближче до ручки ніж до завісів?

8.               Чому на витягнутій руці неможливо втримати такий самий вантаж як і на зігнутій?

9.               Чому качки і гуси ходять вперевалку?

(В залежності від контингенту учнів, їх здібностей, ступеня підготовки, вмінь і навичок даний матеріал розбивається вчителем, на свій розсуд, на дві частини, які опрацьовуються на першому і другому уроках відповідно. В класах з глибокими знаннями з математики доцільно збільшити число розрахункових завдань).

Завдання додому. Опрацювати відповідні параграфи підручника. Виконати одну із розрахункових задач із підручника.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 3

Тема:      Лабораторна     робота    "З'ясування     умови    рівноваги    важеля".

Розв'язування х задач. 

Мета:     Перевірити на досліді правило важеля. Навчити учнів застосовувати   правило моментів при розв'язуванні задач з статики. 

Обладнання: Важіль на штативі, набір тягарців, лінійка, динамометр.

 

Перевірка домашнього завдання проводиться методом фронтального опитування учнів і перевіркою записів в їх зошитах.

1.     Що називають плечем сили? плечем важеля? за яких умов плече сили дорівнює плечу важеля? 

2.     Яка умова рівноваги важеля? 

3.     Що називають моментом сили?

4.     В яких одиницях вимірюється момент сили?

5.     Коли момент сили додатній? від'ємний?

6.     Як формулюється правило моментів? 7. Наведіть приклади проявів важелів в живій природі?

 

Розділ фізики в якому вивчається рівновага тіл називається статикою. Щоб тіло перебувало в рівновазі (не рухалось) потрібно, щоб сума всіх сил, що діють на тіло, дорівнювала нулю. Однак якщо буде задовільнятись лише ця умова то тіло буде мати можливість повертатись (якщо воно має вісь обертання - важіль). Тому для тіла що має вісь обертання необхідною умовою рівноваги сил є ще й рівновага моментів сил. Сума моментів сил що діють на тіло повинна дорівнювати нулю (з урахуванням знаків моментів). При розв'язуванні задач на статику необхідно враховувати вагу всіх точок тіла. Неоднорідне розміщення речовини буде створювати додаткові моменти сил. Якщо важіль однорідний і вісь обертання проходить через його центр, то момент створюваний силою тяжіння рівний нулю і його можна не враховувати. В цьому випадку важіль повинен займати горизонтальне положення. Якщо плечі важеля неоднакові то положення важеля не буде горизонтальним - в цьому випадку момент сили тяжіння не дорівнює нулю – важіль - не зрівноважений.

Після проведення інструктажу по правилах поводження з приладами при виконанні лабораторної роботи, учні записують тему і хід виконання роботи в зошити і приступають до її виконання. 

 

Хід роботи.

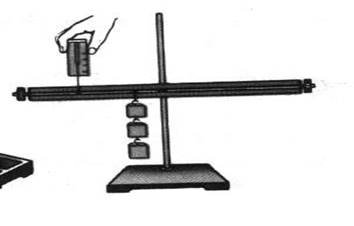
1.                     Закріпити важіль на штативі і зрівноважити його (викручуючи або вкручуючи гвинти на кінцях важеля).

2.                     Підвісити на лівій частині важеля два тягарці (F₁).

3.                     Пересуваючи тягарець, який причіплюємо (F₂) справа, добиваємось рівноваги важеля. Вимірюємо довжину плеч обох сил.

4.                     Знаходимо дослідним шляхом точку в якій потрібно справа підвісити два тягарці (F₂), щоб важіль перебував в рівновазі. Вимірюємо плечі сил.

5.                     Знаходимо величину плеча, де потрібно справа підвісити три тягарці (F₂), щоб важіль перебував в рівновазі.

Знаючи, що кожен тягарець важить 1Н, запишіть дані вимірювань і обчислень в таблицю.

                     F₁                                    F2

   

№ п/п	F1 (Н)	L1 (м)	M1=F1·L1 (Н·м)	F2 (Н)	L2 (м)	M2=F2·L2 (Н·м)	F1/F2	L2/L1
1	2
2	2
3	2

 

Зробити висновок із отриманих результатів.

6.                     Перевірити правило моментів для кількох сил. Зліва в одній точці підвісити два тягарці. Справа тягарці по 1 Н розмістити в трьох точках так щоб важіль перебував в рівновазі. Виміряти плечі сил. Знайти суму моментів всіх сил. Перевірити правило моментів.

7.                     Перевірити чи справджується правило моментів для важеля другого роду. Для цього зліва підвісити три тягарці. Зліва знайти точку в якій потрібно під’єднати динамометр, щоб важіль перебував в рівновазі. Виміряти сили і плечі сил. Перевірити співвідношення: М₁ = М₂.

 

Завдання додому. Задачі із збірника задач.

 

 

 

 

 

 

 

 

 

Урок 4

Тема: Застосування закону рівноваги важеля до блока. Види блоків і їх застосування.

Мета: Ознайомити учнів з основними елементами блока. Пояснити способи їх застосування.

Обладнання: модель рухомого і нерухомого блоків, поліспаст, таблиці.

 

Перевірка розв’язання учнями домашніх завдань.

Повторення опорних понять.

1.     Яка умова рівноваги важеля?

2.     Що називають плечем сили?

3.     Який важіль називають рівноплечим?

4.     Яке співвідношення між силами що діють на важіль і величинами їх переміщень? Швидкостями?

5.     Де використовуються важелі?

6.     Який важіль називають важелем першого роду? другого роду?

 

Одним із різновидностей важеля є блок. Блок це колесо з жолобом (щоб не сповзала вірьовка) закріплене в обоймі. По жолобу блока пропускають вірьовку, трос або ланцюг. Здебільшо блоки використовують під час переміщення вантажів. Нерухомий блок – це блок вісь обертання якого не переміщується під час піднімання вантажу. Рухомий блок – це блок вісь обертання якого переміщується разом з переміщенням вантажу. (Під час пояснення вчитель демонструє блоки і їх дію).

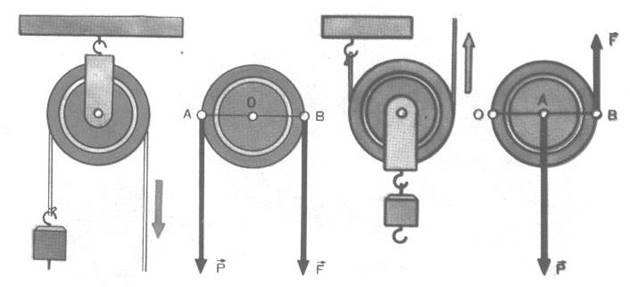
                           Малюнок 1.                                           Малюнок 2.

Нерухомий блок (Мал.1) можна розглядати як рівноплечий важіль в якого плечі сил (АО і ОВ) дорівнюють радіусу колеса (R). Такий блок не дає виграшу в силі (P = F), але дає можливість змінювати напрям сили (від 0 до 180º). Величини переміщень сили і вантажу однакові. Однакова також швидкість руху сили і вантажу.

Рухомий блок (Мал.2) можна розглядати як важіль другого роду, плечі сил якого відносяться як 1:2 (ОА : ОВ). запишемо умову рівноваги важеля стосовно рухомого блока: F·2·R = P·R. Звідси F = P/2. Отже рухомий блок дає виграш в силі в два рази. (Всі пояснення супроводжуються обов’язковими демонстраціями, які підтверджують правильність пояснюваних положень). 

Однак при використанні рухомого блока виграючи в два рази в силі ми в два рази програємо в шляху і швидкості. При всіх застосуваннях блоків необхідно не забувати що блоки і троси (нитки) мають певну масу і на приведення їх в дію (рух) потрібно прикласти додаткову силу, а також що між віссю обертання і блоком існує тертя. Звичайно на практиці застосовують комбінацію нерухомого і рухомого блоків. Вага рухомого блока прикладена до середини блока (плече сили дорівнює R). Сила тертя напрямлена по дотичній до обода блока (плече сили тертя для рухомого блока дорівнює 2R). Щоб підняти рухомий блок вагою Р потрібно прикласти силу: F = F_тертя + P/2. в залежності від конкретних потреб використовують різне сполучення рухомих і нерухомих блоків яке дає потрібний виграш в силі.

 

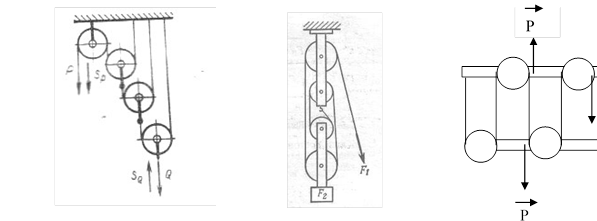
Мал.3 Мал.4                                    Мал.5

Система блоків (Мал.3) дає можливість змінювати напрям прикладеної сили (Р) з допомогою нерухомого блока з одночасним виграшем в силі в 2ⁿ раз (Р = Q/2ⁿ). Де n – кількість рухомих блоків. (В випадку показаному на малюнку виграш в силі становить 8, тому що n = 3, і Р = Q/2³ = Q/8). 

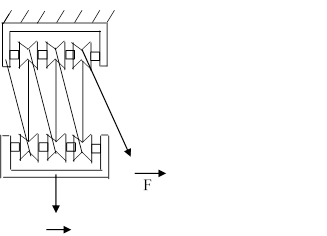
Ступеневий поліспаст (Мал.4) дає виграш в силі в 4 рази (F₁ =F₂/4).

Поліспаст може мати і іншу будову (Мал.5), в цьому випадку виграш в силі теж рівний 4. 

 

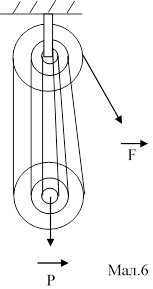                                                                                                                                           P                                                              

                                                                                                                                                          ^Мал.7                                           

 

Блоки можна закріпити і на одній осі (на одній нерухомі а на другій рухомі) Мал.6 і Мал.7. Діаметр всіх блоків може бути різний (Мал.6) або однаковий (Мал.7). Виграш в силі дорівнює 2n, де n – число рухомих блоків. Для систем на Мал.6,7 виграш в силі рівний 6. (F = P/(2n) = P/(2·3) = Р/6).

Збільшуючи кількість блоків можна отримати більший виграш в силі. Однак збільшення числа блоків веде до збільшення сили тертя, яка зумовлює зменшення виграшу в силі.

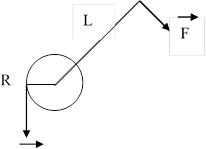Однією із різновидностей важеля є коловорот. Коловорот – це нерухомий блок, який обертається разом із закріпленою в ньому віссю. (Проводиться демонстрація дії коловорота). Одним із застосувань коловорота є використування його в колодязях. Коловорот дає виграш в силі в стільки разів в скільки разів довжина ручки коловорота (L) більша

P                                                  за його радіус (R). F = P·R/L.

 

Задача 1. За допомогою рухомого блока вантаж підняли на висоту 1,5м. На яку висоту при цьому витягнуто вільний кінець вірьовки?

(S_F=2 S_P = 2·1,5 м = 3 м).

Задача 2. Вантаж якої маси можна підняти за допомогою рухомого блока вага якого 20 Н, прикладаючи зусилля 210 Н до вільного кінця вірьовки.

P_блока = 20 H      (P + P_блока)/2 = F,   P + 20 = 210·2,  P = 420 – 20 = 400 (H). F = 210 H           P = m·g,   m = P/g,    g = 10 Н/кг,    m = 400/10 = 40 (кг). m - ?

Задача 3. Як застосувати блок щоб мати виграш у відстані?

 

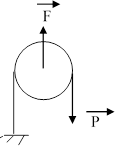(Потрібно силу (F) прикласти до самого блоку а не  до вірьовки. Вантаж Р пройде відстань в два рази

більшу ніж прикладена сила F).

 

 

 

Задача 4. Як можна з’єднати один з одним рухомі і нерухомі блоки, щоб дістати виграш в силі в чотири рази? В шість раз?

Відповідь. Можливі варіанти з’єднань показані на малюнках.

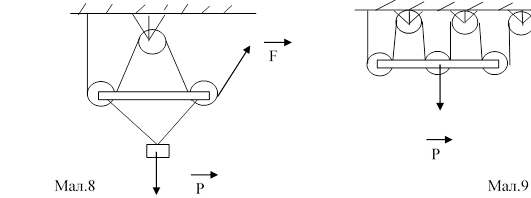
Для Мал.8   F = P/4.  Для Мал.9   F = P/6.  (Можна і так як показано на малюнках 6,7).

Закріплення матеріалу проводимо розв’язуючі задачі поданого нижче типу.

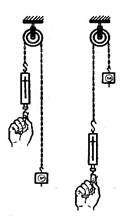Задача 5. Через нерухомий блок перекинуто ланцюг. В якому випадку динамометр          показуватиме       меншу         силу при рівномірному підніманні вантажу? Чому? (В другому. Тому що в першому випадку довжина ланцюга, який потрібно піднімати більша, а ланцюг має певну масу).

 

 

 

 

 

 

 

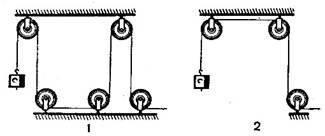Задача 6. В якій із систем нерухомих блоків потрібно прикласти більшу силу для піднімання одного й того самого вантажу якщо тертя в кожному з блоків однакове? (В першому більшу, тому що в першому      випадку      більша кількість блоків, а значить і більша сила тертя).

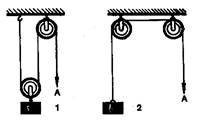Задача                              7.    Для    піднімання одного        й        того   самого       вантажу використовують        дві     системи       блоків.        Чи однакові сили потрібно прикласти в точці А, якщо тертя в кожному блоці однакове, а вага рухомого блока набагато менша від ваги вантажу? (В випадку 1 сила буде менша бо використовується рухомий блок).

 

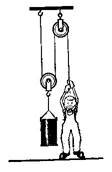Задача 8. Який найбільший вантаж може підняти хлопчик масою 42 кг, користуючись одним рухомим і одним нерухомим блоком стоячи на поверхні Землі. (84 кг).

 

 

 

 

 

 

 

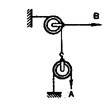Задача 9. Яку силу потрібно прикласти до троса А, щоб трос В був натягнутий із силою 4000 Н?  (2000 Н).

 

 

 

 

Задача 10. Яку силу потрібно прикласти до троса А, щоб трос В був натягнутий із силою 10 кН? (2,5 кН)

 

 

 

 

 

 

 

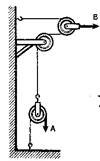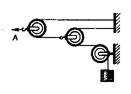Задача 11. З якою силою натягнуто трос А, якщо вага вантажу дорівнює 1000 Н? (4000 Н)

 

 

 

 

Задача 12. За допомогою рухомого блока піднімають вантаж, прикладаючи силу 100 Н. Визначити силу тертя, якщо вага блока дорівнює 20

Н, а вага вантажу 165 Н.

F = 100 H           F = F_тертя + (P_блока + P_{вантажу})/2; 100 = F_тертя + (20 + 165)/2; P_блока = 20 H       100 = F_тертя + 92,5;    F_тертя = 100 – 92,5 = 7,5 (H).

P_{вантажу} = 165 H F_тертя - ?

Задача 13. Вантаж піднімають за допомогою рухомого блока діаметр якого 5 см, а пізніше за допомогою блока діаметр якого 10 см. Чи вплине заміна блоків на виграш в силі? (Вважати блоки невагомими). (Ні)

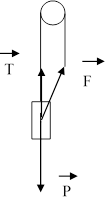Задача 14. Як легше підніматися вгору: лізти по мотузці чи піднімати себе за допомогою блока (дивись малюнок)?

Розв’язання. Людина для піднімання прикладає мускульну силу рук (F) до правого кінця вірьовки, спричинюючи силу натягу вірьовки (T). Сила натягу лівого кінця і правого кінця однакова (вірьовка нерозтяжна). До лівого кінця вірьовки також прикладена вага людини (P) зменшена на мускульну силу рук. Отже до людини прикладено три сили: сила

тяжіння, мускульна сила і сила натягу вірьовки. P = T + F; так як T = F то будемо мати: P = F + F;  P = 2F; F = P/2. Отже використовуючи блок людина для підняття буде прикладати силу майже в два рази меншу за вагу тіла.

 

Завдання додому. Відповідні параграфи підручника.

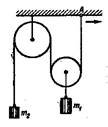Задача 15. В системі яка складається із рухомого і нерухомого блоків, вантажі масою m₁  і m₂ які висять на блоках, перебувають в рівновазі, коли нитки паралельні. Що відбудеться, якщо точку до якої прикріплена нитка (А) переміщувати вправо як показано на малюнку.

Масами блоків знехтувати.

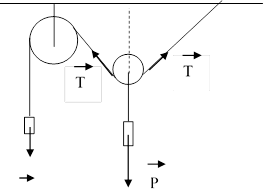Розв’язання. Коли нитки паралельні то сила натягу нитки Т = Р/2. Якщо  нитки на рухомому блоці будуть не паралельні, то сума проекцій сил натягу (Т) цих ниток на вісь ваги (Р) буде меншою за суму сил Т і не буде  зрівноважувати вагу Р (коли нитки паралельні то Т+Т = Р). Тому вантаж Р буде       опускатися а       вантаж        Р/2 підніматися.

 

                  P/2                                                                       

 

 

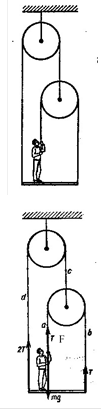Задача 16. З якою силою F повинна людина тягнути вірьовку, щоб втримати дошку в рівновазі, якщо маса людини 60 кг? (Дивись малюнок). Масами дошки, вірьовки і блока знехтувати. 

Розв’язання. Людина прикладає до частини вірьовки (а) мускульну силу F. Так як вірьовка нерозтяжна то на обох частинах вірьовки (а) і (b) сила натягу буде однакова, Т = F. Натяг вірьовки перекинутої через нерухомий блок в обох її частинах (c) і (d) буде рівний T + F = F + F = 2F. Отже до дошки будуть прикладені такі сили: сила натягу вірьовки (d) рівна 2F, напрямлена вверх; сила натягу вірьовки (b) рівна F, напрямлена вверх; сила тяжіння mg зменшена на величину мускульної сили людини F, (mg - F), напрямлена вниз. Так як за умовою дошка перебуває в

рівновазі то: (mg - F) = 2F + F. Звідки отримуємо F = mg/4. підставивши числові дані отримаємо: F = 60·10/4 = 150 (Н).

 

Додаткові завдання.

 

Задача 17.  В якому напрямку буде рухатись тіло А, якщо ручку Р повертати за годинниковою стрілкою?

 

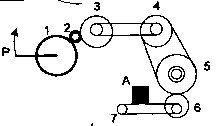
/Відповідь – вліво/.

Задача 18. у системі зображеній на малюнку, перше тіло має швидкість v₁ = 4 м/с. Яка швидкість другого тіла v₂?

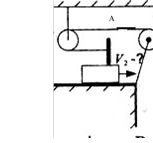
Розв’язання. Оскільки друге тіло рухається вправо із швидкістю v₂ , точка А нитки рухається вліво з такою самою швидкістю, тобто швидкість першого тіла напрямлена вверх. Якщо точка А переміститься на Х вліво, то рухомий блок разом з першим тілом піднімуться на Х/2. це означає, що швидкість точки А (і другого тіла) у 2 рази більша за швидкість першого тіла.

v₂ = 2 v₁ = 8 м/с.

 

Задача 19. В механічній системі, зображеній на малюнку, циліндр А котиться без проковзування із швидкістю v₁ = 2 м/с і намотує на себе нитку. Яка швидкість v₂ тягарця В?

 

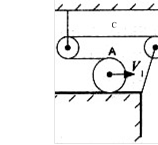
Розв’язання. Точка А циліндра і нитки (С) має швидкість v₃ = 2v₁ =4м/с. Точка С  має таку саму швидкість, що і точка А, але напрямлену вліво. Це означає, що тіло В піднімається вверх із швидкістю v₂ = 0,5 v₃ = v₁ =2 м/с.

 

Задача 20. В механічній системі, зображеній на малюнку, дошка рухається по горизонтальній поверхні з швидкістю v₁ = 1 м/с. Циліндр А котиться без проковзування по дошці з відносною швидкістю v₂ = 2 м/с і намотує на себе нитку. Яка швидкість v₃ тягарця В?

 

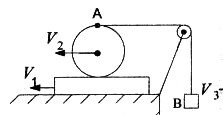
Розв’язання. Швидкість тягарця В дорівнює швидкості точки А циліндра (нитки). Швидкість точки А відносно дошки вдвічі більша за швидкість осі циліндра v₁. v_АВ= 2v₂ . Швидкість точки А відносно поверхні:

v_А = v_АВ + v₁ = 2 v₂ + v₁ = 5 м/с.

 

Задача 21. В механічній системі, зображеній на малюнку, дошка рухається по горизонтальній поверхні із швидкістю v₁ = 2 м/с. Циліндр А котиться без проковзування по дошці з відносною швидкістю v₂ = 1 м/с і намотує на себе нитку. Яка швидкість v₃ тягарця В?

 

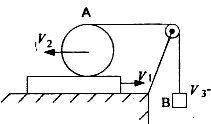
Розв’язання. Швидкість тягарця В дорівнює швидкості точки А нитки (циліндра). Швидкість точки А відносно дошки v_А = 2 v₂ . Швидкість  точки А відносно поверхні: v_АВ = v_А - v₁ = 0. v₃ = v_АВ = 0.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 5.

Тема: Похила площина і її різновиди. Лабораторна робота “Визначення коефіцієнта корисної дії похилої площини”.

Мета: Ознайомити учнів із ще одним простим механізмом – похилою площиною. Навчити практично визначати коефіцієнт корисної дії похилої площини та з’ясувати його залежність від кута нахилу до горизонту.

Обладнання: похила площина, клин, гвинт, динамометри, бруски, лінійка, транспортир.

 

Активізація опорних знань.

1.     Перевірити правильність виконання домашніх задач.

2.     Що називають ККД механізму?

3.     Як визначають ККД механізму?

4.     Від яких факторів залежить ККД механізму?

5.     Як можна збільшити ККД механізму?

 

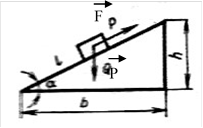Крім важелів до простих механізмів належить похила площина. Тобто площина розміщена під кутом до горизонту. Її використовують, щоб підняти або викотити вантаж на деяку висоту. Для опису руху по похилій площині  вводять такі позначення. L – довжина похилої площини, h – висота похилої площини. Щоб підняти вантаж на висоту h, пересуваючи його по похилій площині, потрібно прикласти силу F яка менша за вагу тіла Р. На основі “золотого правила” механіки: А_F = А_P; F·L = P·h; Або L/h = P/F. Звідси можна сформулювати таке правило:

піднімаючи вантаж уздовж похилої площини виграємо в силі у стільки разів у скільки довжина схилу похилої площини більша за її висоту. Частина роботи витрачається на перемагання тертя, тому А_к < А_з. І коефіцієнт корисної дії буде рівним: ККД = А_к/A₃ = F·L/ P·h. Різновидом похилої площини є клин і гвинт. 

Клин – тверде тіло, поздовжнім перерізом якого є прямокутний трикутник (Мал. 2). Найчастіше використовують клин у формі двох прямокутних клинів, складених своїми основами (Мал. 3). Клин становить 

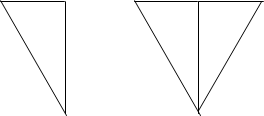основну частину колючих, ріжучих, стругальних інструментів: ножиць, ножа, сокири, стамески, рубанка, лемеша плуга, тощо. “Колюча зброя” багатьох тварин і рослин – кігті, роги, зуби і колючки – по формі нагадують клин. На клин подібна і загострена форма голови швидкісних риб.

            Мал. 2                           Мал. 3             Багато із цих клинів мають дуже гладенькі

тверді поверхні (для мінімуму тертя),

завдяки чому і досягається їх велика гострота.

 

 

 

 

 

 

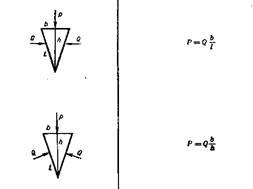
Співвідношення між прикладеною силою P і силою Q яка отримується при використанні клина показані на малюнку. Виграш в силі в першому випадку становить Q/P = l/b а в другому Q/P = h/b.

 

Запитання. Щоб забити гвіздок у тонку дощечку, не розколовши її, рекомендується спочатку обрубати зубилом загострений кінчик гвіздка. Чому такий гвіздок не розколює дощечку? //Вістря гвіздка, подібно до клина, розсуває деревину, а обрубаний кінець цієї дії не створюватиме//.

Гвинтом називають прямий циліндр, який має на поверхні гвинтову лінію (нарізку). Гвинтовою лінією називається лінія, описана на поверхні циліндра гіпотенузою прямокутного трикутника, накрученого на циліндр, при цьому основа трикутника має дорівнювати довжині кола циліндра. Гвинт використовується в домкраті, гвинтовому пресі, свердлику. //Проводиться одночасна демонстрація//.

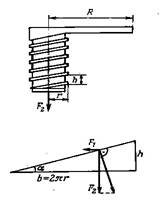Гвинт можна подати як похилу площину, навиту на вісь. Введемо позначення. F₁ – сила, яка діє на відстані r від осі гвинта і необхідна для повороту гвинта. F₂ – сила, яка діє в напрямку осі гвинта, h – крок гвинта, r - середній радіус різьби. α – кут нахилу різьби (похилої площини). Тоді F₁/F₂ = h/b = tg α. Або F₁ = F₂· tg α. Якщо сила F₁ прикладена на деякій відстані R від осі гвинта, то F₁/F₂ =h/b = h/2πR або F₂ = F₁·2πR/h. Виграш в силі при застосуванні гвинта дорівнює: F₂/F₁ = 2πR/h.

Задача. При рівномірному переміщенні вантажу масою 15 кг по похилій площині динамометр прив’язаний до нього, показує силу 40 Н.

Обчислити ККД похилої площини, якщо довжина її 1,8 м, висота 30 см.

m = 15кг        h = 30 см = 0,3 м,  ККД = А_к/А_з,  А_з = F·L, 

F = 40 Н        А_з =40·1,8=72 (Дж). А_к = P·h, P = m·g, P = 15·10 = 150 (Н). L = 1,8 м        А_к = 150·0,3 =45 Дж,         ККД = 45/72 = 0,625.

h = 30 см ККД - ?

 

Прочитати в підручнику хід виконання лабораторної роботи. Після виконання роботи учні повинні зробити висновок що ККД збільшується із збільшенням кута нахилу.

Виконання роботи.

1.     Виміряти вагу бруска динамометром.

2.     Виміряти висоту і довжину похилої площини.

3.     Переміщуючи рівномірно по похилій площині брусок, прикладаючи силу до динамометра який зчеплений з бруском, визначити покази динамометра. Ця сила буде рівна силі тертя.

4.     Обчислити корисну і затрачену роботу.

5.     Визначити ККД похилої площини.

6.     Дані вимірювань і обчислень занести в таблицю.

№ п/п	Р (Н)	h (м)	Ак = P·h (Дж)	F (Н)	L (м)	Аз = F·L (Дж)	ККД = Ак/Аз

7.     Повторити вимірювання збільшуючи кут нахилу похилої площини.

8.     Зробити висновки.

 

Завдання додому. Вивчити матеріал відповідних параграфів і запитань до них, закінчити оформлення звіту про виконання лабораторної роботи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 6.

Тема: Робота, потужність, механізми. Розв’язання задач.

Мета: Поглибити знання учнів про роботу, потужність, механізми. Навчити застосовувати теоретичні знання при розв’язуванні задач. Прививати вміння правильно вибирати формули, визначати з них потрібні величини. Підготувати учнів до проведення підсумкового оцінювання по даній темі.

Повторення опорних понять.

1.     Назвати формули обчислення роботи.

2.     Як обчислюється потужність?

3.     Які одиниці вимірювання роботи? Потужності?

4.     Як знайти ККД механізму?

5.     Яка робота називається корисною? Затраченою?

 

Задача 1. Вага ковша з вугіллям 3000 Н. Знайти потужність двигуна підйомного крана, якщо за 5 с ківш рівномірно підніметься на висоту 15 м. P = 3000 H        N =A/t;       A = P·h; t = 5 c                 A = 3000·15 = 45000 (Дж). h = 15 м             N = 45000/5 = 9000 (Вт). N - ?

Задача 2. Яку роботу виконує підйомний кран, рівномірно піднімаючи алюмінієву плиту об’ємом 2 м³ на висоту 10 м?

V = 2 м³           A = P·h;    P = m·g;   m = ρ·V.

h = 10 м          ρ_{алюмінію} = 2700 кг/м³;    m = 2700·2 = 5400 (кг).

Алюміній       Р = 5400·10 = 54000 (Н).  А - ?                А = 54000·10 = 540000 (Дж).

 

Задача 3. Обчисліть роботу, виконану під час піднімання ящика на висоту 12 см за допомогою важеля, одне плече якого в 10 раз довше від другого, коли сила, що діє на довге плече, дорівнює 150 Н.

S_P = 12 см      S_P = 12 см =0,12 м;

L_F = 10·L_P       A = F·S_F; S_F =10·S_P;      S_F = 10·0,12 = 1,2 (м);

F = 150 H       A = 150·1,2 = 180 (Дж). A - ?

Задача 4. За допомогою рухомого блока рівномірно піднімають протягом 0,5 хв. ящик з цеглою на висоту 12 м, діючи силою 320 Н. Чому дорівнює потужність, яку розвивають під час піднімання ящика? t = 0,5 хв.     t = 0,5 хв =0,5·60 с = 30 c,     N = A/t,   A = F·S_F.

S_P = 12 м     Для рухомого блока S_F = 2S_P;  S_F = 2·12 = 24 (м). F = 320 H    A = 320·24 = 7680 (м); N - ?             N = 7680/30 =256 (Вт).

Задача 5. Стержень, на одному кінці якого підвішено вантаж масою 12 кг, перебуває в рівновазі в горизонтальному положенні, якщо його підперти на відстані 1/5 довжини стержня від вантажу. Чому дорівнює вага стержня? Вважати що вага стержня прикладена до його середини.

 

 

 

                  m = 12 кг      F = m·g,                                             _O

L_F = 1/5 L F = 12·10 = 120 (H), P - ?                 L_P = L/2 – L/5 = 3·L/10.

M_F = M_P;  M_F = F·L_F; M_P = P·L_P;

F·L_F = P·L_P;  120·L/5 = P·3·L/10,

                  24 = P·3/10;  P = 240/3 =80 (H).                             _F

Задача 7. Чи міг Архімед підняти Землю?

“Дайте мені точку опори, і я, підніму Землю!” – такий вигук легенда приписує Архімеду, геніальному механіку давності, який відкрив закон важеля. “Одного разу Архімед, - читаємо ми в Плутарха, - написав сіракузькому царю Герону, якому він був родич і товариш, що довільною силою можна підняти будь-який вантаж. Захоплений силою доведення, він додав, що якщо б була інша Земля, він перейшовши на неї, зрушив би з місця нашу”.

Архімед знав, що немає такого вантажу, якого не можна було б підняти самою малою силою, якщо використати важіль: досить лише прикласти цю силу до дуже довгого плеча важеля, а коротке плече заставити діяти на вантаж. Тому він вважав, що натискаючи на надзвичайно довге плече важеля, можна силою рук підняти і вантаж, маса якого рівна масі землі. 

Але, якщо б великий механік давності знав, яка величезна маса Землі, він напевно не висказав би свого гордого виклику. Уявімо, що Архімеду дана та “друга Земля”, та точка опори, яку він шукав, уявімо дальше, що він заготовив важіль потрібної довжини. То для цього щоб підняти Землю на 1 см йому потрібно було б тридцять тисяч більйонів років (3·10¹⁰ років). Справді, маса Землі 6·10²⁴ кг. Якщо людина безпосередньо може підняти лише 60 кг, то щоб “підняти Землю” йому потрібно прикласти силу рук до довгого плеча важеля, яке більше за коротке в 10²³ раз (6·10²⁴/60 = 10²³)! Тоді поки короткий кінець важеля підніметься на 1 см (0,01 м) то довгий пройде шлях 10²¹ м (0,01 м·10²³ = 10²¹ м). Такий шлях повинна була б пройти рука Архімеда, щоб “підняти Землю” на 1 см. Скільки ж часу потрібно для цього? Якщо вважати що Архімед здатен підняти 60 кг на 1 см за 1 с, то для підняття Землі на 1 см потрібно 10²¹с (1 с·10²¹ = 10²¹ с), тобто тридцять тисяч більйонів років. Ніякі пристосування геніального винахідника не допомогли б йому зменшити цей час. “Золоте правило” механіки говорить, що виграш в силі призводить до втрати в часі. Навіть якби Архімед рухав руку з найбільшою можливою в природі швидкістю (3·10⁸ м/с) то й при цьому він

“підняв би Землю” на 1 см лише за десять мільйонів років (10⁶).

 

Завдання додому. Підготуватися до тематичного оцінювання. Вчитель роздає учням (групам учнів) індивідуальні завдання різного ступеня складності.