Як навчитися розв’язувати задачі з фізики
Так як, одна проблема, над якою працюю «Формування в учнів алгоритмічних прийомів розв'язання фізичних задач», то велику увагу приділяю формуванню і розвитку алгоритмічних прийомів розв'язування задач.
Як навчитися розв’язувати задачі з фізики
Так як, одна проблема, над якою працюю «Формування в учнів алгоритмічних прийомів розв’язання фізичних задач», то велику увагу приділяю формуванню і розвитку алгоритмічних прийомів розв’язування задач. Для цього на своїх уроках використовую опорні конспекти, алгоритми розв’язку, блок-схеми.
Для чого треба вміти розв’язувати задачі з фізики
Розв’язування фізичних задач у на уроках фізики:
1. Сприяє більш виразному формуванню фізичних понять, більш різнобічному і глибокому розумінню, міцному освоєнню змісту навчання.
2. Створює і зміцнює навички й уміння в застосуванні фізичних законів для пояснення явищ природи і для розв’язання практичних питань. Таким чином, реалізується єдність теорії і практики.
3. Допомагає наповнити фізичні формули конкретним змістом, дати учням навик у виборі формул і в користуванні ними.
4. Є одним з дієвих способів встановлення міжпредметних зв'язків.
5. Дозволяє здійснити повторення пройденого матеріалу, організувати контроль знань.
З досвіду роботи з учнями, на початку найбільшу складність під час розв’язування задач викликають знаходження невідомих величин з формул. Тому можна застосовувати деякі прийоми під час виконання цих дій.
Наприклад, учні вчаться «шифрувати» три-чотири формули, які містять по 3-4 величини в одному «трикутнику».
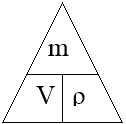 Щоб знайти шукану величину, закриваємо її в трикутнику – отримуємо необхідну формулу (m= Vρ, V =
Щоб знайти шукану величину, закриваємо її в трикутнику – отримуємо необхідну формулу (m= Vρ, V = ![]() , ρ =
, ρ = ![]() ). Такі трикутники допомагають учням уникати помилок під час застосування тієї чи іншої формули. (Дивись рисунок). При цьому необхідно пояснювати фізичний зміст кожної формули, щоб не було механічного запам’ятовування.
). Такі трикутники допомагають учням уникати помилок під час застосування тієї чи іншої формули. (Дивись рисунок). При цьому необхідно пояснювати фізичний зміст кожної формули, щоб не було механічного запам’ятовування.
Що стосується виведення загальної формули, то пропонуємо виконувати це в такій послідовності (застосовуючи прийом «ланцюжок» або «матрьошка» під час підстановок:
- написати формулу для шуканої величини;
- проаналізувати, чи всі величини, що входять до формули мають чисельні значення за умовою;
- якщо всі – приступати до обчислень;
- якщо не всі – написати формули для невідомих величин;
- якщо в останню написану формулу входять тільки відомі величини, починати виконувати підстановки – останню – в передостанню і так далі «знизу вгору» (для методу «матрьошка».
Коли загальна формула виведена, виконують обчислення, одночасно перевіряють, виконуючи дії над одиницями вимірювання.
Приклад. Скільки потрібно часу, щоб насос потужністю 50 кВт з шахти глибиною 150 м відкачав 200 м3 води?
 Дано: Розв’язання
Дано: Розв’язання
![]() N = 50 кВ = 50000 Вт
N = 50 кВ = 50000 Вт
h = 150 м
v = 200 м3
![]() ρ = 1000 кг/м3
ρ = 1000 кг/м3
t - ? с
В результаті підстановок отримаємо формулу t = ![]() . Під час обчислень використовуємо скорочення одиниць вимірювання для перевірки правильності розв’язку.
. Під час обчислень використовуємо скорочення одиниць вимірювання для перевірки правильності розв’язку.
t = 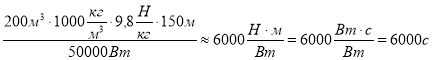
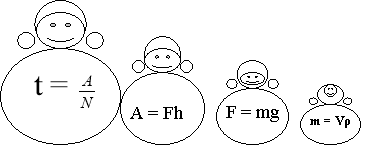
На уроках розв’язування задач доцільно використовувати формули-книжки за якими зручно слідкувати за поступовим виведенням ускладненої формули.
В старших класах обов’язково необхідно навчити учнів користуватися алгоритмом перетворення формули 2-го закону Ньютона у відповідності з даною фізичною ситуацією. Розглянемо наступний алгоритм.
- Аналіз прочитаної умови задачі, скорочений запис даних величин, та тих, котрі необхідно визначити.
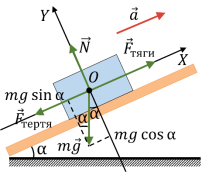
- Виконання рисунку з показом діючих сил, прискорень та швидкостей.
- Запис основного рівняння динаміки для даного виду руху у векторній формі.
- Раціональний вибір системи координат (часто пов’язують з рухомим тілом) та запис основного рівняння динаміки в проекціях на осі
- Аналіз отриманих рівнянь та робота з ними, визначення невідомих величин через задані, або ті котрі необхідно визначити.
- Розв’язування рівнянь з використанням початкових умов.
- Запис отриманих результатів в раціональній формі, обчислень числових значень та їх аналіз.
Приклад 2. Автомобіль масою 2 т піднімається на гору, нахил якої становить 0,2. На ділянці шляху 32 м швидкість руху автомобіля зросла від 21,6 км/год до 36 км/год. Вважаючи рух автомобіля рівноприскореним, визначте силу тяги двигуна, якщо коефіцієнт тертя дорівнює 0,02.
|
Дано:
|
Розв’язання
Система відліку, пов’язана з Землею інерціальна. Швидкості тіл малі порівняно зі швидкістю світла. Рух поступальний. Отже, закони Ньютона в даній ситуації можуть бути застосовні.
Запишемо другий закон в проекціях на координатні осі:
Це рівняння (1) та (2). |
- Робимо аналіз даних рівнянь.
Бачимо, що є два рівняння з чотирма невідомими. Сила реакції опори з другого рівняння (2): ![]() . Підшукуємо ще два рівняння: Сила тертя
. Підшукуємо ще два рівняння: Сила тертя ![]() . (3).
. (3).
- Виходячи з умови задачі знайдемо прискорення:
 (4)
(4)
Підставимо знайдені величи в першу формулу (1), маємо:
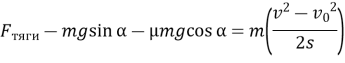
Маємо загальну формулу
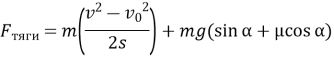
- Не забуваємо зробити перевірку одиниць:
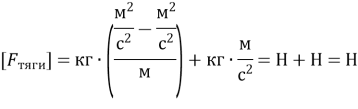
Підставляємо значення:
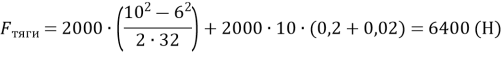
Не забуваємо проаналізувати даний результат.
Відповідь:![]()
Слід зауважити, що захоплюватися алгоритмічними методами і прийомами недоцільно, але на кожному етапі вивчення фізики можна підібрати 1-2 алгоритми з основних тем.


про публікацію авторської розробки
Додати розробку

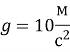
 Аналіз умови задачі
Аналіз умови задачі