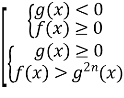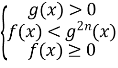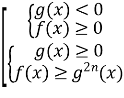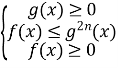Як одне запитання допомагає розв'язати ірраціональну нерівність

Як одне правильно поставлене запитання допомагає розв’язати ірраціональну нерівність

В математиці ставити питання

важливіше за вміння їх розв’язувати.

Г. Кантор

Часто при розв’язуванні ірраціональних нерівностей учні використовують той же прийом, що і при розв’язуванні ірраціональних рівнянь: піднесення обох частин нерівності до одного і того ж степеня. Але практика показує, що саме при цьому виникає найбільше помилок, особливо при розв’язуванні нерівностей виду (або ).

Згадаємо, як розв’язується рівняння виду .

Зазначимо спочатку, що найкращим способом для розв’язування даного рівняння є перехід до рівносильної системи

.

Це зумовлюється тим, що ОДЗ часто не виключає сторонні корені, при цьому потрібна ще перевірка.

Але при розв’язуванні нерівностей повна перевірка практично неможлива, тому потрібно йти тим же шляхом переходу до рівносильної системи чи сукупності систем нерівностей.

Як же учневі при цьому запам’ятати послідовність і доцільність тієї чи іншої нерівності у системі?

Багаторічний досвід підказує, що перед розглядом теоретичного обґрунтування даного питання бажано розглянути декілька прикладів, коли вираз g(x) набуває числового значення.

Приклад 1. Розв’язати нерівність .

Область допустимих значень: х ≥ 2,5.

Піднесемо обидві частини нерівності до квадрата: 2х – 5 < 9.

Звідси х < 7. Враховуючи область допустимих значень, маємо хϵ[2,5; 7).

Відповідь: [2,5; 7)

Приклад 2. Розв’язати нерівність .

Підкреслюємо, що за означенням арифметичного квадратного кореня нерівність не має розв’язків. (Піднесення обох частин до квадрату привело б до відповіді з попереднього прикладу).

Відповідь: розв’язків немає.

Приклад 3. Розв’язати нерівність .

Область допустимих значень: х ≥ 2,5.

Піднесемо обидві частини нерівності до квадрата: 2х – 5 > 9.

Звідси х > 7. Поглинаючи область допустимих значень, маємо хϵ(7; +∞).

Відповідь: (7; +∞).

Приклад 4. Розв’язати нерівність .

Область допустимих значень: (х ≥ 2,5) і є розв’язком нерівності, оскільки за означенням арифметичний квадратний корінь більший за будь-яке від’ємне число при всіх допустимих значеннях змінної.

Відповідь: [2,5; +∞).

Тепер учні готові для того, щоб зрозуміти, навіщо задавати головне питання: Чи може бути g(x) < 0?

Можна побудувати алгоритм дій для розв’язання нерівностей даного типу і подібних нерівностей.

 Слід пояснити учням, чому так будується сукупність (перша система – приклад 4, коли розв’язком є область допустимих значень, у другій системі – приклад 3, коли значення f(x) більше квадрата виразу, що є невід’ємною величиною). А у випадку з системою нерівностей усі дії цілком логічні.

 Аналогічно будуємо алгоритм для нестрогих нерівностей (можна запропонувати учням побудувати його самостійно).

Після цього учням набагато легше розв’язувати подібні нерівності, запам’ятовування змінюється розумінням. На прикладах закріплюємо матеріал.

Приклад 5. Розв’язати нерівність .

Запитання: Чи може бути 4 – х < 0? Так.

Тому складаємо сукупність нерівностей.

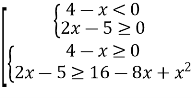
Для першої системи хϵ(4; +∞), для другої хϵ(3; 4]. Об’єднуємо проміжки.

Відповідь: (3; +∞).

Приклад 6. Розв’язати нерівність .

Запитання: Чи може бути 4 – х < 0? Ні.

Тому складаємо систему нерівностей.

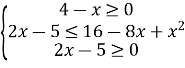
Маємо

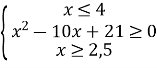
Звідси  хϵ [2,5; 3)

Відповідь: [2,5; 3)

Приклад 7. Розв’язати нерівність

Запитання: Чи може бути  х + 3a < 0? Ні.

Тому складаємо систему нерівностей.

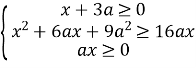
Маємо

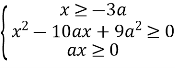
Оскільки ах ≥ 0, то а і х мають один і той же знак. При від’ємних а і х не виконується нерівність х ≥ – 3а, система розв’язків не має, тому а ≥ 0 і х ≥ 0.

Якщо а = 0, то х ≥ 0.

Якщо а > 0, (х ≥ 0), то перша і третя нерівності виконуються при всіх невід’ємних значеннях х. Залишається розв’язати нерівність

.

Розкладемо на множники:   .

При додатних значеннях а маємо 9а>а, тому хϵ[0; а] [9а; +∞)

Відповідь: Якщо а < 0, то нерівність розв’язків не має;

якщо а = 0, то х ≥ 0;

якщо а > 0, то хϵ[0; а] [9а; +∞).

Останній приклад показує, як можна застосувати набуті знання і уміння для виконання нерівності з повним поясненням, наприклад, для виконання завдання №35 під час ЗНО 2020.