ЗМІСТ

 

Вступ………………………………………………………………………………...3

 

1. Інтерактивні технології навчання ………………………………………………..4

 

2. Застосування нових інформаційних технологій при вивчення математики…...7

 

 

3. Використання засобів інформаційних технологій навчання під час розв’язання стереометричних задач обчислювального характеру …………………………..14

 

4. Використання елементів методів проектів та комп’ютерної підтримки на уроках фізики …………………………..………………………………………….23

 

 

5. Урок-лабораторна робота ………………………………………………………...31

 

6. Урок – гра ………………………………………………………………………….33

 

7. Урок – захист творчих робіт учнів ……………………………………………....37

 

 

Висновки …………………………………………………………………………..50

 

Список використаних джерел …………………………………………….51

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВСТУП

 

«Скажи мені-і я забуду,

Покажи мені –і я запитаю

Дай мені діяти самому - і я навчуся»

(мудрість китайського філософа)

 

 

На сьогоднішній день залишається відкритими питання про нові принципи, системи, програми та методики формування знань учнів. В наш час використання інтерактивних технологій в навчальному процесі відкриває перспективи його якісного вдосконалення. Пошуки нових форм навчально-виховного процесу сьогодні не тільки виправдані, але як ніколи актуальні.

Нові методи навчання, нестандартні форми уроку допомагають розбудити інтерес учня до досліджуваної проблеми, сприяють більш глибокому вивченню теми уроку. Взагалі, подальшого вивчення потребують питання застосування методів навчання, які забезпечують формування у учнів творчих умінь, розвитку їх пізнавальної діяльності, самостійності, індивідуальних творчих здібностей.

Важливим аспектом застосування інтерактивних технологій є оновлення структури уроків. Кожен вчитель знає, що такі уроки краще запам’ятовуються учнями, викликають зацікавленість і бажання взяти участь в уроці. В нашій роботі ми пропонуємо використання різних форм роботи на уроках математики, фізики та інформатики.

 

Мета: Ознайомлення вчителів математичних дисциплін з сучасними інтерактивними технологіями у процесі навчання.

 

Об’єкт: процес вивчення застосування інтерактивних технологій в навчанні.

 

Предмет: це процес формування знань школярів з математичних дисциплін.

 

Виходячи з мети, об’єкту та предмету нашої роботи можна сформулювати такі завдання:

1. Вивчити стан проблеми в психолого-педагогічній та методичній літературі.
2. Розкрити суть поняття інтерактивні технології навчання.
3. Введення засобів інформаційних технологій навчання під час розв’язання стереометричних задач обчислювального характеру.
4. Розробити уроки на застосування різних форм організації діяльності учнів.

 

Гіпотеза: рівень знань учнів підвищиться, якщо особливу увагу приділяти використанню інтерактивних технології навчання.

 

 

 

 

ІНТЕРАКТИВНІ ТЕХНОЛОГІЇ НАВЧАННЯ.

 

Як відомо, в шкільній освіті  існує безліч методів навчання, різні типи уроків, які переслідують одну єдину мету - засвоєння знань учнями. Заохочувальним є впровадження нововведень та їхнє гармонічне уливання в устояну структуру уроку.

Учень і вчитель є рівноправними суб'єктами навчання. Організація інтерактивного навчання припускає моделювання життєвих ситуацій, використання рольових ігор, загальне рішення питань на підставі аналізу обставин і ситуації. Зрозуміло, що структура інтерактивного уроку буде відрізняться від структури звичайного уроку, це також вимагає професіоналізму і досвіду викладача. Тому в структуру уроку включаються тільки елементи інтерактивної моделі навчання – інтерактивні технології, тобто включаються конкретні прийоми й методи, які дозволяють зробити урок незвичайним і більше насиченим і цікавим. Хоча можна проводити і повністю інтерактивні уроки.

У педагогіці розрізняють кілька моделей навчання:

1) пасивна - учень виступає в ролі <об'єкта> навчання (слухає й дивиться)

2) активна - учень виступає <суб'єктом> навчання (самостійна робота, творчі завдання)

3) інтерактивна - inter (взаємний), act (діяти). Процес навчання   здійснюється в умовах постійної, активної взаємодії всіх учнів.

Інтерактивні технології навчання - це така організація процесу навчання, у якому учню неможливо не приймати участь – в колективному, взаємодоповнюючому, заснованому на взаємодії всіх його учасників процесу навчального пізнання.

Форми організації діяльності учнів на уроці .

   1) групова - навчає одна людина, більше тих, хто слухає, чим тих, хто говорить; 

  2) кооперативна (колективна) - спосіб навчання в малих групах.

Кожна людина має дві потреби: потреба росту й бути в безпеці, прилучившись до групи людей. При кооперативному способі навчання досягається спільна діяльність заради досягнення загальних цілей. У дітей з'являється впевненість у собі, вони пишаються навчальними успіхами один одного.   Кооперативне навчання може існувати не тільки в групах, але й у парах.

Окремої уваги вимагає організація роботи в малих групах. Коли потрібно вирішити складні проблеми колективним розумом.

Ось приклади деяких конкретних методик роботи в малих групах:

 «Діалог» - його суть полягає в тім, що групи шукають погоджене рішення, а результат роботи повинен бути відображений у вигляді схеми, перерахування ознак, кінцевому тексті, що потім записується в зошитах. Ця методика включає протистояння й критику позицій тієї або іншої групи, а вся увага зосереджена на сильних моментах позиції інших. Експерти фіксують загальні погляди і під завершення роботи дають узагальнену відповідь на завдання, що записується всіма.
«Синтез думок» - схожий на попередній метод, з тією різницею, що учні не ведуть записи на дошці, а всі записи роблять на аркушах, які потім передають наступній групі. У цьому аркуші підкреслюються думки, з якими дана група не згодна. Експерти обробляють ці аркуші, зіставляючи написане, роблять загальний звіт, що потім обговорює весь клас.

«Спільний проект» - у цьому випадку групи одержують завдання різного змісту, які висвітлюють проблему з різних боків. При завершенні роботи кожна група робить звіт і робить свої записи на дошці. Із цих записів ніби складається спільний проект, що рецензується й доповнюється групою експертів.

«Пошук інформації» - метод застосовується, якщо потрібно якось пожвавити сухий, найчастіше нецікавий матеріал. Суть його в тім, що відбувається командний пошук інформації, що доповнює вже наявну (прочитану вчителем лекцію або домашнє завдання) з наступними відповідями на питання. Для груп розробляються питання, відповіді на які можна знайти в підручниках, роздавальному матеріалі, документах і т.д. Завжди визначається час, протягом якого потрібно проаналізувати інформацію й знайти відповіді на питання.
«Коло ідей» - метою є вирішення гострих спірних питань, складання списку ідей і залучення всіх учнів до обговорення питання. Всі групи повинні виконувати одне і теж завдання, що складається з декількох питань (позицій), які представляються групами по черзі. При відповідях кожна із груп озвучує тільки один аспект проблеми, а вчитель задає питання по колу доти, поки ідеї не закінчаться. Це виключає можливість доповіді всієї інформації однією групою.

Всі перераховані методи інтерактивних методів навчання ставляться до технологій кооперативного навчання, коли учням потрібно скооперуватися для виконання завдань вчителя, активної роботи на уроці, засвоєння матеріалу і вироблення навичок спілкування при дискусії й аргументації своїх позицій. Величезним плюсом даного виду навчальної діяльності є залучення абсолютно всіх учнів класу у спільну роботу. Труднощі полягають в умінні вчителя організувати роботу учнів і привчити їх до такої роботи як постійної. Звичайно, це не все, що можна використовувати. На основі цих методів можна будувати інші, або придумувати щось принципово нове, у цьому і полягає перевага інтерактивного навчання.

Технологій інтерактивного навчання існує величезна кількість. Кожний вчитель може самостійно  вигадувати нові форми роботи із класом.

Вид роботи:

1) Робота в парах.

2) Ротаційні (змінні) трійки.

3) Карусель.

4) Робота в малих групах.

5) Акваріум.

6) Незакінчена пропозиція.

7) Мозковий штурм.

8) Броунівський рух.

9) Дерево рішень.

10) Суд від свого імені.

11) Громадські слухання.

12) Рольова (ділова) гра.

13) Метод прес.

14) Займи позицію.

15) Дискусія.

16) Дебати.

Карусель, коли утворюється два кільця: внутрішнє й зовнішнє. Внутрішнє кільце – це сидячі нерухомо учні, а внутрішнє – учні через кожні 30 секунд змінюються. Таким чином, вони встигають проговорити за кілька хвилин декілька тем і постаратися переконати у своїй правоті співрозмовника.

Технологія Акваріум полягає в тім, що декілька учнів розігрують ситуацію в колі, а інші  спостерігають і аналізують.

Броунівський рух припускає рух учнів по всьому класі з метою збору інформації із запропонованої теми.

Дерево рішень - клас ділиться на 3 або 4 групи з однаковою кількістю учнів. Кожна група обговорює питання й робить записі на своєму «дереві» (аркуш ватману), потім групи міняються місцями і дописують  на деревах сусідів свої ідеї.

Займи позицію. Зачитується яке-небудь ствердження і учні повинні підійти до плаката зі словом «ТАК» або «НІ». Бажано, щоб вони пояснили свою позицію.

Свіча. По колу передається запалена свіча і учні висловлюються про різні аспекти навчання.

Інтерактивні технології навчання стимулюють пізнавальну діяльність і самостійність учнів. Ця модель бачить спілкування в системі вчень-вчитель, наявність творчих (часто домашніх) завдань як обов'язкових. Інтерактивна модель своєю метою ставить організацію комфортних умов навчання, при яких всі учні активно взаємодіють між собою. Інтерактивна творчість вчителя й учня безмежна. Важливо тільки вміло направити її для  досягнення поставлених навчальних цілей.

 

 

 

 

                            Підготувала:

                                                   Вчитель математики та інформатики  - Ликова І.П.                    

 

 

 

 

 

 

 

 

 

 

 

 

ЗАСТОСУВАННЯ НОВИХ ІНФОРМАЦІЙНИХ

ТЕХНОЛОГІЙ ПРИ ВИВЧЕННІ МАТЕМАТИКИ

 

В наш час використання засобів сучасних інформаційних технологій в навчальному процесі відкриває перспективи його якісного вдосконалення. Загальна комп’ютеризація та інформатизація освіти повинна бути застосована на єдиному понятійному апараті і широкому застосуванні методів інформатики при вивченні інших шкільних предметів.

Ефективне застосування засобів нових інформаційних технологій у навчальному процесі передбачає перш за все формування та оволодіння провідними компонентами сучасної інформаційної культури (на базі основ комп’ютерної грамотності) вчителями всіх спеціальностей. Слід зазначити, що вчитель повинен бути перш за все кваліфікованим фахівцем у своїй галузі, будь то біологія чи історія, література, мова чи математика, а також він повинен добре вміти правильно інтерпретувати повідомлення, які видаються комп’ютером. Знати принципи побудови та дії комп’ютерів і програм для комп’ютерів при цьому зовсім не обов’язково, якщо це не стосується пов’язаної з фахом предметної області.

Інформатика тісно зв’язана з іншими шкільними навчальними дисциплінами. Тобто, знання, вміння та навички, які учні отримують при вивченні інформатики, необхідні при вивченні інших шкільних предметів, коли комп’ютер буде активно допомагати процесу їх вивчення на базі різноманітних навчаючих програм.

Комп’ютер грає велику роль в індивідуалізації навчання учнів всіх рівней здібностей. Вчитель математики за допомогою комп’ютера може задавати вправи, які являються додатковими до регулярних програм для відпрацювання навичок у відповідності з можливостями кожного учня, а також вироблення навичок використання основних понять та ідей при розв’язуванні задач різноманітного роду.

Система діалогу „Запитання  – відповідь”, де можна застосовувати комп’ютер:

• як тренажер;
•   як репетитор;
• як пристрій, який моделює визначення предметні ситуації; можна також використати для проведення самостійних робіт (перевірка вироблення учнями практичних навичок), контрольних робіт та заліків.

Для останніх можна використати контрольно – діагностичну систему, яка має за ціль перевірку теоретичних знань і практичних навичок за допомогою комп’ютерного тестування. Спеціальна програма виводить на екран запитання тексту і дає на нього до 5-ти варіантів відповідей, один з яких правильний. Учневі досить вказати правильну, на його думку, відповідь і перейти до наступного запитання. Послідовність виведення запитань тестів на сусідні комп’ютери різна. Час відповіді обмежується 3-10 хвилинами. Залежно від кількості відповідей автоматично виставляється оцінка. Запитання, які залишалися без відповідей, зараховуються як неправильні.

Використання такої системи дає можливість учителю математики під час занять акцентувати увагу на стимулюванні процесів саморозвитку. На уроках математики з використанням інформатики всіх учнів очікує напружена і цікава робота. Кожен працює в міру своїх здібностей і можливостей.

На уроках змішаного типу учень ставиться в такі умови, що відсидітися за спинами інших не можливо. Учитель уміло керує діяльністю учнів, пропонуючи їм такі завдання і вправи, щоб їхнє мислення було спрямоване на самостійне розв’язування нестандартних творчих завдань, розвиток індивідуальних здібностей.

Учитель свідомо ставить кожного учня в такі умови, щоб вибір подальших дій залежав від нього, а тому учні набувають впевненості, поваги до себе, професійності.

Але слід зауважити, що до використання комп’ютерів у школі потрібно поставити деякі вимоги. По-перше – в рамках освітньої галузі у школах без поглибленого вивчення математики і інформатики не слід намагатися вчити дітей „дорослим” мовам програмування. По-друге – візуалізація (наочність) – потужний засіб при вивченні математики. Наприклад, у викладанні тригонометрії помітну допомогу може справити наочне подання перетворень графіків тригонометричних функцій на комп’ютері. Такий підхід дозволить значно скоротити час, який відводиться на викладання теоретичних положень, а також з більш природних, наочних позицій роз’яснити способи побудови графіків тригонометричних функцій.

Наявність комп’ютерів і відповідного програмного забезпечення дозволяє розширити коло прикладів, багато з яких будуть виникати у новій освітній технології.

Реалізація комп’ютерного підходу потребує розробки методичного і методологічного забезпечення, створення відповідних програм, великої роботи по підготовці педагогів.

Але широке впровадження нових інформаційних технологій в практику шкільного навчання буде сприяти створенню єдиного підходу до організації навчального процесу, який надасть викладачам потужний апарат, що дозволить не тільки пояснювати новий матеріал, але й отримувати через комп’ютер дійсно об’єктивну інформацію про хід навчального процесу.

З метою втілення в практику роботи нових інформаційних технологій, за темою: „Комп’ютерна підтримка уроків математики в старшій школі” вчителями, методичним об’єднанням математиків СЗШ № 90 було проведено семінар – практикум, з метою представлення доцільності використання комп’ютерної техніки в старшій школі та перспектив введення елементів комп’ютерної грамотності в основній школі.

Нижче наводяться приклади фрагментів уроків різного типу, а саме:

• урок систематизації і узагальнення знань з алгебри в 10–А класі за темою: „Тригонометричні рівняння”.
• урок вивчення нового матеріалу з алгебри в 11–А класі за темою: „Похідна ”.

 

 

Тема: Зростання та спадання функції. Дослідження функції на монотонність (фрагмент).

Мета: Формування вмінь та навичок в знаходженні проміжків монотонності

Хід уроку:

1.    Актуалізація опорних знань:

1.   Означення (висвітлюється на моніторі). Функції зростаючі та спадні називаються монотонними.

Функція називається  зростаючою на проміжку J,якщо для довільних x₁ та x₂, якщо x₂ > x₁, то ƒ(x₂) > ƒ(x₁).

2.   Ознаки зростання (спаду) функції.

Якщо функції у = ƒ(х) у внутрішній точці х₀ проміжка J має похідну ƒ′(x₀) та       ƒ′(х₀) > 0 (ƒ′(x₀) < 0), то функція у = ƒ(х)  в кожній точці J, то у = ƒ(х) зростає (спадає) на J.

Значити, щоб дослідити функцію на монотонність, треба знайти проміжки з її області визначення, де ƒ′(х) > 0,  ƒ′(х) < 0.  

2. Приклади розв’язування вправ (на моніторі)

Повторюється алгоритм дослідження функції на монотонність.

1. Знайти область визначення заданої функції у = ƒ(х);
2. Знайти похідну ƒ′(х);
3. Розв’язати нерівності:

а) ƒ′(х) > 0, вказати проміжки зростання функції у = ƒ(х)

б) ƒ′(х) < 0, вказати проміжки спадання функції у = ƒ(х)

1) Дослідити у = х³ – 3х² – 24х на монотонність

Розв’язування:

D(у) = R, ƒ′(х)= 3х² – 6х – 24

ƒ′(х) > 0, якщо 3х² – 6х – 24 > 0, х² – 2х – 8 > 0.

Розв’язуємо методом інтегралів

х² – 2х – 8 = 0, х₁ = -2, х₂ = 4

         +                –               + 

                 -2                4  

ƒ′(х) > 0, якщо х  (– ∞; –2)  (4;+ ∞)

ƒ′(х) < 0, якщо х   (–2;4)

Таким чином, функція зростає на (– ∞; –2)  (4;+ ∞), спадає на (–2;4)

2) Дослідити на монотонність у = х +

Розв’язування:

D(у) = (– ∞; 0)  (0;+∞);

у′(х) = 1 – ;  1 – > 0;  > 0;

Розв’язуємо методом інтегралів

         +                –               + 

                  0                2  

у′(х) > 0, якщо х  (– ∞;0)  (2;+ ∞)

у′(х) < 0, якщо х   (0;2)

III) Тренувальні вправи

На моніторі: Бажаєте потренуватися так / ні  

Вчитель: Без вірного розв’язування цих двох вправ неможливий перехід до наступних. Програма побудована так, що у кожного з вас вправи індивідуальні.

Приклади тренувальних вправ:

1.         Дослідити на зростання функції

у = 2х²  – 8х + 4;

у = –х² + 6х + 1;

2.         Дослідити на спадання функції

у = 2х³ – 15х² – 36х + 15;

у = 6х² – 30х – 80;

IV) Контрольні вправи

Вчитель: В процесі розв’язування ви можете, якщо виникли труднощі, нажати на клавіши:

F1 – підказка

1. Означення

2. Ознаки монотонності

3. Приклад 1.

4. Приклад 2.

5. Таблиця похідних

6. Повернення

F2 –  калькулятор

В кінці розв’язування всіх контрольних завдань вам буде виставленна оцінка, кількість підказок. За відведений час ви можете встигнути зробити декілька варіантів контрольних завдань. Після закінчення кожного блоку завдань на моніторі висвітлюється оцінка, яку ви одержали. Всі результати в кінці роботи занесіть в карту особистих досягнень.

Приклади контрольних завдань

1. Дослідити на зростання:

у = х² – 2х + 4

2. Дослідити на зростання:

у =

3. Дослідити на спадання:

у = , тощо

В кінці уроку учні самостійно виводять собі середній бал.

 

                                             Підготували:

вчитель математики –Яцушко А.І.,

вчитель математики –Шевчук Т.В.,

вчитель математики –Скрипченко О.Д.

 

 

 

 

Тема: Тригонометричні рівняння, які зводяться до алгебраїчних.

Мета:  узагальнити і систематизувати знання учнів основної тригонометричної  тотожності і наслідків з неї формул подвійного аргументу;

• виховувати в учнів охайність, точність при розв’язуванні рівнянь і при введенні в ПК;
• розвиток вольових зусиль, цілеспрямованості і навичок самоконтролю учнів.

Тип уроку: узагальнення і систематизація знань, умінь і навичок учнів.

Хід уроку:

1. Мотивація навчальної діяльності

Вчитель: оголошує тему і мету уроку;

зачитує епіграф до уроку, який записаний на дошці.

Вчитель інформатики: ставить перед дітьми задачу згадати ключові моменти при роботі з ПК, які допоможуть їм в засвоєнні поставленої мети.

2. Узагальнення теоретичного матеріалу. На моніторі висвічується спосіб розв’язування тригонометричних рівнянь.

Вчитель: розглянемо перший спосіб: приведення до одноіменної тригонометричної функції.

2 Sin²x – 3Sin x + 1 = 0

Sin x = y     y  < 1

Вчитель: чому ставиться умова  y  < 1?

2у² – 3у + 1 = 0

D = 3² – 4*2*1 = 9 – 8 = 1

D > 0, то

y =         y =

y₁ = 1                  y₂ =  

Обидва корені задовольняють умові y  < 1

Вчитель: згадайте як знайти тригонометричного рівняння Sin x = а, окремий випадок Sin x = 1.

Sin x = 1             Sin x =

х = + 2k, k  Z        x = ( - 1)*arcsin + n, n  Z

Відповідь:  + 2k, k  Z;          ( - 1)*+ n, n  Z

Вчитель: розглянемо другий приклад (на моніторі висвітлюється приклад 2)

Cos2x + Sin²x + Sin x = 0,25

Вчитель: назвіть формулу косинус подвійного аргументу (висвітлюється на моніторі).

Cos2x = Cos²x  - Sin²x

маємо:   Cos²x  - Sin²x + Sin²x + Sin x = 0,25

Вчитель: назвіть основну тригонометричну тотожність

Sin²x + Cos²x = 1

маємо:   1 - Sin²x + Sin x = 0,25

Нехай  Sin x = у,  y  < 1, тоді

4у² – 4у – 3 = 0

D = 4² + 4*4*3 = 64

у₁ = 1,5  у₂ = –

у₂ – не задовольняє умові y  < 1

Sin x = –

х = (– 1) n, n  Z

Вчитель: зробіть висновки, як розв’язуються тригонометричні рівняння; способи зведення до алгебраїчних і які формули при цьому використовуються.

Після обговорення на моніторі висвітлюються висновки:

• Якщо рівняння шляхом тотожних перетворень можна звести до алгебраїчного рівняння, то його розв’язують шляхом підстановки.

При цьому використовують:

•  основна тригонометрична тотожність і наслідки з неї, тотожність

tg * ctg = 1

•  формула Cos2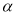= Cos²x - Sin²x і її наслідки

Cos 2 = 1 – 2 Sin²

Cos2 = 2Cos²x – 1

На моніторі висвітлюється другий спосіб „Розкладання на множники”

Sin2х + 3 Sin х = 0

Вчитель: згадайте формулу сінуса подвійного аргументу

Sin2х = 2Sin х * Cos х

маємо:   2Sin х * Cos х + 3Sin х = 0

Sin х * ( 2Cos х + 3) = 0

Вчитель: сформулюйте необхідну і достатню умову, при якій добуток дорівнює нулю.

Sin х = 0,  або 2Cos х + 3 = 0

х = n, n  Z    Cos х = , не задовольняє умові y  < 1

Приклад 4 (висвітлюється на моніторі)

Sin х + Sin3х = Sin2х

Вчитель: назвіть формулу додавання сінусів

маємо:  2 Sin *Cos – Sin2x = 0

2Sin2x * Cos x – Sin2x =0

Sin2x *( 2Cos x – 1) = 0

Sin2x = 0     2Cos x = 1

2x = n, n  Z    x =  arccos  + 2n, n  Z   

x = , n  Z      x =  n, n  Z   

3. Перевірка знань, умінь і навичок учнів на комп’ютері:

– кожен одержує завдання індивідуальне;

– розв’язує рівняння і відповідь заносить до комп’ютеру;

– після цього на моніторі висвітлюється оцінка;

• далі учень одержує слідуюче завдання; 
•   результати заносяться до карти досягнень.

Приклади для самостійної роботи.

1 – 5Sin x + 2Cos²x = 0

Cos x – Cos3x = Sin2x

Розв’язуючи рівняння учні можуть звернутися за підказкою (клавіша F1).

 

 

                                              Підготували:

вчитель – математики Яцушко А.І.,

вчитель – математики  Шевчук Т.В.,

вчител– математики Скрипченко О.Д.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Використання засобів інформаційних технологій навчання під час розв’язання стереометричних задач обчислювального характеру

 

Використання в школі при вивченні точних  дисциплін засобів новітніх інформаційних технологій навчання (НІТН), зокрема педагогічних програмних засобів, дозволяє поєднати високі обчислювальні можливості ЕОМ при дослідженні різноманітних об'єктів з унаочненням результатів на всіх етапах розв'язування задач.

Використання GRAN-3D дає можливість економити навчальний час за рахунок виключення рутинних обчислювальних операцій, озброює учнів ефективними наочними методами розв'язування широкого класу стереометричних задач.

Аналіз стану викладання геометрії в середній школі показує, що мотивація, наочність, інтерес до предмета, а також формування прийомів розумової діяльності, зокрема узагальнення та систематизації, можуть бути ефективно реалізовані поєднанням традиційної методики навчання з впровадженням у навчальний процес нових інформаційних технологій:

1) як засіб наочності - для полегшення: процесу оперування просторовими образами; розуміння теоретичного матеріалу (аналіз понять га їх відношень); осмислення та усвідомлення умови поставленої задачі; виділення головного;

2) як калькулятор — для полегшення складних обчислень;

3) для самоконтролю;

4) для діагностики навчальних досягнень учнів.

При вивченні шкільного курсу геометрії, зокрема стереометрії, незаперечним є факт величезної ролі наочності в процесі вивчення геометричних об'єктів у тривимірному просторі. Сучасні математичні методи поступово перетворюються у допоміжні дидактичні інструменти, які після програмної реалізації за допомогою потужної комп'ютерної техніки перетворюються в супровідні засоби навчального процесу, що сприяють активізації роботи дітей .

Впровадження комп'ютерних технологій у процес викладання математичних дисциплін, зокрема геометрії, сприяє досягненню педагогічної мети за рахунок використання комп'ютерних засобів: ілюстрації геометричних понять, створення та вивчення інформаційних і математичних моделей явищ і процесів, розвитку геометричної інтуїції.

За допомогою комп'ютера як засобу моделювання учень отримує графічний образ поняття разом із пов'язаною з ним числовою інформацією, що спрощує усвідомлення змісту нового поняття, сприяє розвитку образного мислення та формуванню просторових уявлень.

Основною метою узагальнюючого повторення на рівні системи понять є вироблення в учнів уміння порівнювати вивченні поняття, встановлювати нові зв'язки і відношення між ними, прослідкувати розвиток понять в їх ієрархічних залежностях, тобто встановлювати підпорядкування виду роду у випадку порівняння понять чи утворення нових.

Повторення на рівні системи понять спрямоване також на виявлення спільних властивостей групи понять та поширення їх на інші поняття. При цьому на перший план висувається аналіз взаємозв'язків понять. Спочатку виділяються відношення, які встановлюють зв'язки між елементами одного й того самого класу математичних об'єктів, потім відношення, які встановлюють зв'язки між елементами різних класів.

Тема «Многогранники» є однією із основних тем курсу стереометрії. Основні питання, які розглядають в цій темі, є такі: зображення многогранників, побудова перерізів многогранників площиною, визначення кута між гранями многогранника або між площиною перерізу й однією з його граней, знаходження площі поверхні і об'єму многогранника.

При вивченні теми «Многогранники» в багатьох задачах учні зустрічаються з необхідністю побудови кута між прямою і площиною.

Практика показує, що коли в задачі йдеться про такі кути, більшість учнів будує їх правильно. Характерним для цих задач є те. що площина, на яку проектується пряма-горизонтальна. Коли ж у задачі йдеться про кут між прямою і не горизонтальною площиною, то більшість учнів не можуть правильно будувати кут. Помилки учнів зумовлені тим. що поняття перпендикуляра, проведеного з даної точки на площину, вони пов'язують з розумінням відстані від даної точки до горизонтальної площини .

З метою формування системних знань про кут між прямою та площиною потрібно розв'язувати задачі, в яких доводиться проектувати пряму на площину, розмішену не горизонтально. Використання ППЗ GRAN 3D дозволяє розглянути геометричні об'єкти в динаміці, що полегшує процес аналізу.

Розв'язувати такі задачі з учнями варто під час вивчення многогранників та в процесі заключного повторення стереометрії у випускному класі. Наведемо розв’язання декількох задач.

Розв'язувати задачі за допомогою використання ППЗ GRAN-3D.

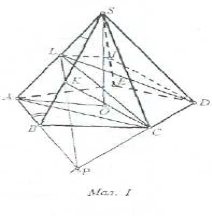
Задача 1. У правильній чотирикутній піраміді побудуйте кут між діагоналлю основи i площиною бічної грані.

Розв’язання: На початку розв'язування задачі доцільно пригадати означення

кута між прямою і площиною (кутом між прямою і площиною називається кут між цією прямою і її проекцією на площину). З означення випливає, що для побудови кута між прямою і площиною треба побудувати прямокутну проекцію цієї прямої на дану площину, за допомогою послуг Об’єкт/ Створити Базовий/ Правильна чотирикутна піраміда будуємо правильну чотирикутну піраміду NABCD (мал.1).

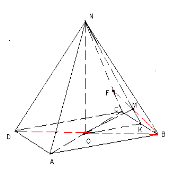
                                                                 мал.1

Відмітимо в основі піраміди діагоналі BD і AC. Для цього, відмітивши відповідні точки, за допомогою послуг Об’єкт/ Створити з екрану/ Ламана побудуємо дані діагоналі.

Побудуємо кут між діагоналлю BD площиною бічної грані BNC . Для нього потрібно побудувати проекції двох точок прямої BD на площину BNC/ Точка B лежить у площині грані BNC. Побудуємо ще  наприклад, проекцію точки O. Проведемо OK┴BC і NK┴BC, використовуючи послугу Об’єкт/ Створити з екрану/ Ламана. За теоремою про три перпендикуляри NK┴BC. Отже, BС перпендикулярна до площини трикутника CSK. Це означає, що площини BNC і NOK також перпендикулярні. Будуємо OM┴NK. Оскільки NK— пряма перетину двох взаємно перпендикулярних площин, то OM— перпендикуляр до площини грані BNC. Пряма BF є проекцією прямої BD на площину грані BNC. Кут DBF — шуканий.

Іншим прикладом може бути:

Задача 2. Дано прямий паралелепіпед. Побудуйте кути нахилу його більшої діагоналі до площин бічних граней.

Розв’язання: Будуємо прямий паралелепіпед ABCDA1B1C1D1 (мал. використовуючи послуги Об’єкт/ Створити Базовий/ Прямий паралелепіпед. Відмітивши точки A1 і С побудуємо за допомогою послуг Об’єкт/ Створити з екрану/ Ламана діагональ A1C. У прямому паралелепіпеді більша діагональ проектується на більшу діагональ основи. Нехай у паралелограмі ABCD кут при вершині A — гострий. Тоді AC— більша діагональ основи, A1C— більша діагональ паралелепіпеда. Спроектуємо вершину A1 на гра­ні BB1C1C і CC1D1D. Для цього досить з A1 провести висоти A1M і A1K паралелограма A1B1С1D1, використовуючи послуги Об’єкт/ Створити  (вони лежать зовні паралелограма, оскільки кут D1A1B1 — гострий). Відмітивши точки C, M, і K, за допомогою послуг Об’єкт/ Створити з екрану/ Ламана побудуємо відрізки CM і CK— проекції A1C на площини відповідних граней BB1C1C і CC1D1D. Тому кути A1CM і A1CK — шукані (м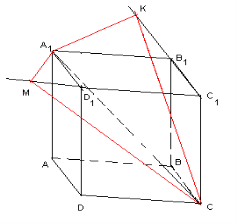ал.2).                                                                             мал.2

 

Порівняльний аналіз „класичного” способу розв'язування даних задач і способу, який передбачає використання програмного засобу GRAN 3D, дозволяє зробити наступні висновки:

1. Використання ППЗ GRAN 3D  полегшує учням з наочно-образним типом мислення процес аналізу і синтезу, зокрема дозволяє уникнути хибного враження, що продовження сторони C1D1 лежить у площині грані AA1D1D (задача № 2) або що CM перетинає CB (задача № 1).

2. Можливість розглянути дані геометричні об'єкти в динаміці полегшує процес аналізу взаємозв'язків понять при узагальненні на рівні системи понять, дозволяє шляхом моделювання ефективніше підвести учнів до розуміння змісту явищ і процесів.

3. Послуга „фонове зображення ” дозволяє виділити шукані елементи, зокрема плоскі кути A1MC і AKC (задача № 2) іншим кольором, що покращує сприйняття і полегшує процес формування образу геометричного об’єкта, сприяє формуванню цілісного уявлення про матеріал.

Вході експериментальної перевірки запропонованої методики ми пропонували учням розв’язати стереометричні задачі обчислювального характеру аналітично („класичним” - способом) і з використанням ППЗ GRAN-3D та співставили отримані результати і час, витрачений на обчислення.

 

Задача. Правильну п'ятикутну піраміду, висота якої 5 лін. од., а сторона основи 3 лін. од., перетнуто площиною,  що проходить через сторону основи і середину протилежного бічного ребра  піраміди. Знайти площу та  периметр утвореного перерізу піраміди.

Спочатку розв'яжемо задачу аналітично, а щоб не ускладнювати кінцеві вирази, будемо виконувати проміжні  обчислення.

Аналітичний спосіб розв’язання задачі.

 

Розглянемо утворений переріз CKLID (мал. 1): КС = LD, KL=LI (оскільки піраміда SАВСDЕ правильна), СD=3 лін. од. (за умовою). Площа п'ятикутника СKLID складається з площ трьох трикутників:                        Sckld = Scld+Sdli+Sckl=Scld+2Sckl (оскільки трикутники СKL та DLI рівні). Щоб знайти площі вказаних трикутників, необхідно знайти довжини їх сторін СК, KL та LC (LС=LD). Відповідно периметр обчислюється за формулою Pcklid = CK+KL+LI+ID+CD=2KL+CK+CD.

LC можна знайти з трикутника LSС, але перед цим необхідно встановити довжину бічного ребра піраміди та величину кута LSС (або величину рівного йому кута ASC).

Знайдемо довжину бічного ребра піраміди. Розглянемо прямокутний трикутник АSО (точка О — центр описаного навколо основи кола).

S0=5 лін.од. (за умовою). Оскільки для правильного n- кутника має місце рівність R=, де an- довжина сторони  n-кутника, а R-радіус описаного навколо нього кола, то  AО =  лін. од. Отже, скориставшись теоремою Піфагора.  маємо:  АS === 5.613596 лін. од.

Величину кута LSС можна встановити з рівнобедреного трикутника АSС, але для нього необхідно знати довжину сторони АС. З рівнобедреного трикутника АВС маємо: АС²=АВ²+ВС²-2·АВ·ВС·соsАВС (за теоремою косинусів). Але оскільки АВ=ВС=3 лін. од. (за  умовою),  а  кут   АВС ==108°, то AC=3·=4,554102 лін. од. Отже, всі сторони трикутника АSС відомі.       Скориставшись теоремою косинусів для трикутника АSС, маємо:

АС²=АS²+SС²-2·AS·SC·соsАSС,             соsАSС=1-= 0.626143.

Повернемося до трикутника LSС. Відомі дві його сторони та кут між ними: LS=,   SC=AS,   LSC=ASC.       

Отже, LС =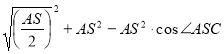=AS·=4,433877 (за теоремою косинусів).

Залишилось знайти LK і КС. Для подальших обчислень необхідно встановити величину кута АВS. З рівнобедреного трикутника АSВ, скориставшись теоремою косинусів,  отримаємо:

соsABS=== 0,267208.

Розглянемо рівнобедрений трикутник ВСР: СВР = ВСР = 180°- АВС , а оскільки сума кутів опуклого n-кутника дорівнює 180°(n - 2),

то   СВР =180°- =72°.  Тоді  ВР=== =4.854102, АР=АВ+ВР = 7.854102.

З трикутника АLР маємо: LР = ===7,601571  (за теоремою косинусів).

За відомими сторонами АL, LР і АР, скориставшись теоремою косинусів ще раз, знайдемо кут АРL:   cosAРІ. = =-0.934557.

Для трикутника КВР мають місце наступні співвідношення:

 ==   →  KP=BP·,   KB=BP·                        - (за теоремою синусів).

Оскільки ВКР=180°-KBP-KPB=ABS-APL,  KBP=180-ABS, KPB=APL, sin(180-ABS)=sinABS,  

то KP=BP=5.807079,

 KB=BP=2.144199.

Оскільки LP = LK+KP,  то LK=LP-KP = 1.794492.

Скориставшись теоремою косинусів, з трикутника KBC отримаємо:

КС = == 3.187461.

Отже, LС, LK і KC знайдено. Для обчислення площі трикутників СLD і CKL доцільно скористатись формулою Герона:

S =,  де а, b,c— довжини сторін трикутника, а,p— його півпериметр.

Для трикутників СКL та СLD маємо:

Pckl==4.707915,   Sckl=2.3900607.

Pcld==5.933877,    Scld=6.258662.

Таким чином, площа перерізу становить Scklid=Scld+Sckl=11.039876 кв. од.  Периметр дорівнює РСKLID=2·1,794492+2·3,187461+3 = 12.963906 лін. од.

А тепер спробуємо розв'язати задачу з використанням ПК за допомогою ППЗ GRAN-3D. Вважатимемо, що програму вже завантажено і на екрані відкрито її головне вікно.

Розв'язування будь-якої задачі зводиться до створення моделі стереометричного об'єкта і виконання операцій, що фігурують в умові задачі. Даний програмний засіб дозволяє оперувати моделями таких геометричних (та просторових) об'єктів як точка, відрізок (або ламана), площина, многогранник, поверхня обертання та довільна поверхня, що визначається рівнянням виду z=f(х,у).

В умові фігурують об'єкти «правильна п'ятикутна піраміда», «точка» (як середина бічного ребра піраміди), «площина». «переріз» (як об'єкт — результат виконання операції «переріз»). Отож необхідно створити моделі об'єктів «правильна п'ятикутна піраміда», «точка» та «площина», що задовольняють умову задачі, та виконати операцію «переріз».

Для створення моделі піраміди зручно скористатися послугою програми „Створити базовий об'єкт”. У вікні „Завдання базових стереометричних об'єктів”, що з'явиться, на вкладинці „Правильна піраміда” встановимо лівий перемикач у положення „Висота” і введемо у полі введення під цим перемикачем значення „5”. Далі встановимо перемикач типу завдання нижньої основи у положення „Сторона” та введемо у поле введення під цим перемикачем значення „З”. Введених параметрів цілком достатньо для автоматичного обчислення за програмою інших параметрів, необхідних для створення многогранника. Після натиснення кнопки  „Створити” з'явиться вікно „Конструювання просторового об'єкту” з вкладинкою «Многогранник”, де можна змінити (якщо не потрібно) деякі параметри створюваного об'єкта. Ми лише змінимо назву об'єкта на „Правильна п'ятикутна піраміда”, а його колір змінимо на синій (за замовчуванням програма встановлює чорний колір). Після натиснення кнопки „Оk” модель піраміди буде створено: зображення п'ятикутної піраміди з'явиться у полі зображення головного вікна, а назва — у переліку об'єктів (мал. 1).

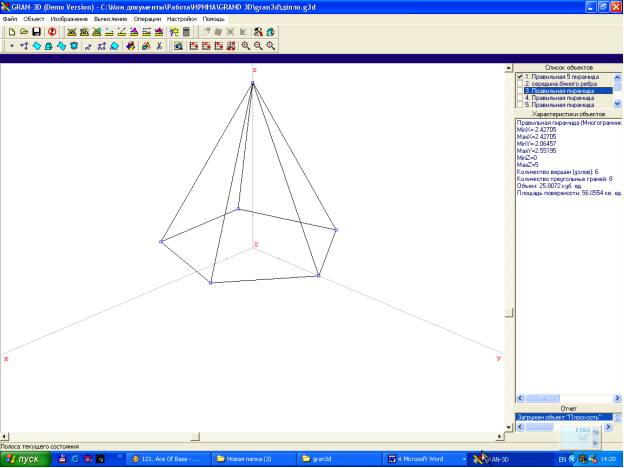
 мал.1

Далі потрібно створити об'єкт «Точка», що відповідає середині одного з бічних ребер піраміди. Для нього необхідно встановити просторові координати цієї точки, що не важко зробити, якщо відомі координати кінців ребра. Якщо підвести вказівник „мишка” до будь-якої вершини піраміди на зображенні, у полі інформування (у нижній частині головного вікна) з'являться просторові координати цієї вершини. Скориставшись цією властивістю програми, встановимо координати вершини, у якій сходяться бічні ребра піраміди (X1=0, У1= 0, Z1 = 5) та координати будь-якої вершини, що належить основі (наприклад, координати най лівішої на зображенні вершини X2=1,5, Y2=-2.064573, Z2 =0 з'являться у полі інформування при наведенні вказівника „миша” до зображення вказаної вершини). Не важко обчислити (за допомогою послуги програми „Калькулятор”) координати середини ребра з кінцями в означених вершинах:

X==0.75,       Y==-1.0322865,    Z= =2.5.

Встановивши перемикач типу об'єкта (над переліком об'єктів) у положення „Точка”, звернемося до послуги головного меню програми Об’єкт/ Створити. У вікні „Конструювання просторового об'єкта”, що з'явиться, на вкладниці „Точка” введемо знайдені координати середини ребра, а у полі введення „Назва об'єкта” введемо „Середина бічного ребра”. Після натиснення кнопки „Оk” об'єкт буде створено (мал.2).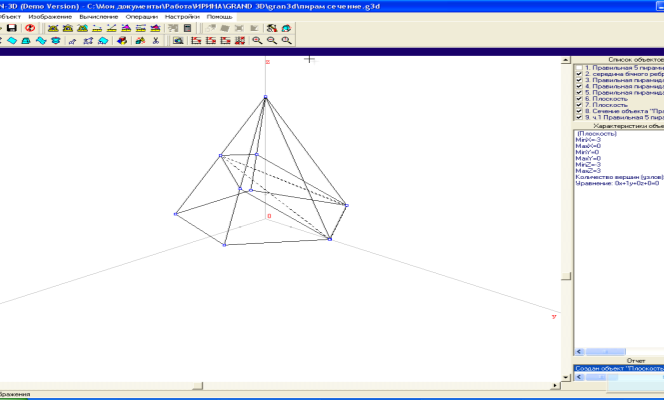

                                                            мал.2

Для задання площини перерізу зручно скористатись послугою програми „Об'єкт/Створити з екрану”: у полі зображення слід лише вказати три точки, що визначатимуть площину. Для нього послідовно підводимо вказівник „мишки” та натискаємо ліву кнопку „мишки” на зображенні точки „Середина бічного ребра” та на зображеннях вершин сторони основи піраміди, протилежної до вибраного бічного ребра. У вікні „Конструювання просторового об'єкта”, що з'явиться після вказання третьої точки, на вкладинці „Площина” введемо назву об'єкта „Площина перерізу” та натиснемо кнопку „Оk”.

Залишилось лише виконати операцію перерізу піраміди площиною. Для нього доцільно скористатися послугою програми „Операції/Виконати переріз” та за відповідними запитами програми у полі зображення за допомогою „мишки” вказати площину перерізу та многогранник, стосовно якого виконується операція. Після виконання операції у полі звіту з'явиться результат обчислення площі та периметра утвореного перерізу (відповідно 11,039855 кв.од. та 12,963595 лін. од.), а також буде створено два нових об'єкти-многогранники: „ч. 1. Правильна п'ятикутна піраміда” та «ч. 2. Правильна п'ятикутна піраміда”, що є частинами базової піраміди в різних півпросторах відносно площини перерізу. Надалі утвореними об'єктами можна оперувати як окремими моделями.

Для унаочнення моделей стереометричних тіл доцільно скористатися послугою програми „Зображення/Режим півтонового зображення”, завдяки чому об'єкти зображуються з врахуванням видимості ліній і площин, чим досягається „реалістичність” зображення.

Не важко переконатись, що відповіді, отримані під час розв'язування задачі двома вказаними різними способами збігаються з досить високою точністю, але при ньому час, витрачений на розв'язування задачі за допомогою ППЗ GRAN-3D, значно менший, ніж час, витрачений на відшукання розв'язку за „класичним” методом. Так, на розв'язування задачі „класичним” способом (виконання малюнка, відшукання способу розв'язування, обчислення) витрачено близько тридцяти хвилин, причому    80% часу було витрачено на побудову малюнка та виконання обчислень, і лише 20 % — на аналіз. І хоча наведена задача досить цікава, важко сподіватися, що її можна встигнути розв'язати за один урок на заняттях з геометрії. На розв'язування ж цієї задачі за допомогою ППЗ GRAN-3D (створення моделей, виконання операцій) було затрачено близько двох хвилин. При цьому важливим є те, що на створених моделях можна розв'язати цілий ряд обчислювальних задач (наприклад, обчислити об'єм базової піраміди або об'єми многогранників. утворених в результаті виконання перерізу, знайти довжини ребер, площі граней многогранників тощо). Вся „рутинна” обчислювальна робота виконується програмою автоматично, залишаючи учням час на дослідницьку діяльність.

Щодо методичного аспекту використання означеного ППЗ у школі, то слід підкреслити, що GRAN-3D призначений, перш за все, для підвищення ефективності навчально-пізнавальної діяльності учнів, надання цій діяльності творчого, дослідницького спрямування за рахунок появи можливостей швидкого отримування відомостей про об'єкти та залежності, що досліджуються, проводити обчислювальні експерименти, підтверджувати або спростовувати гіпотези тощо.

Слід зауважити, що можливості використання розглядуваного програмного засобу не обмежуються розв'язуванням задач наведених типів.

 

 

                               Підготувала:

                                                      Вчитель математики та інформатики  - Ликова І.П.

                         

 

 

 

 

 

 

 

               

 

 

 

 

Використання елементів методів проектів та компютерної підтримки

 

ТЕМА:  В  МИРЕ  ДИАГРАММ.

ЦЕЛЬ:

Выработать у учащихся определенные умения и навыки работы с разными видами диаграмм: построение, чтение,  редактирование и форматирование.

ЗАДАЧИ:

Образовательные: Познакомить с различными видами диаграмм; дать представление о применении диаграмм; выработать умения строить, редактировать и форматировать диаграммы.

Воспитательные: Показать роль диаграмм в окружающем мире; вовлечь  в активную практическую деятельность; воспитывать внимание, находчивость, аккуратность, самостоятельность и самокритичность.

Развивающие:     Научить работать с дополнительной литературой и другими источниками информации (Интернет); готовить доклады выступать перед аудиторией, умение анализировать, выделять главное, обобщать и делать выводы.

 

Тип урока:  Формирования знаний, умений и навыков.

 

Вид урока:   Урок с применением компьютера.

 

Формы работы:  Групповая, индивидуальная.

 

ОБОРУДОВАНИЕ:

Персональный компьютер, прикладная программа Excel, Мудрая Сова, жетоны, раздаточный материал.

 

 

Структура урока:

1. Организационно-психологическая часть. (3мин.)
2. Подготовка к сознательной обучающей работе: постановка целей, мотивация. (3 мин.)
3. Актуализация знаний и умений. (5 мин.)
4. Обобщение знаний и умений. (11 мин.)
5. Систематизация вовремя выполнения практической работы. (15 мин.)
6. Итог урока. (5 мин.)
7. Домашнее задание. (3 мин.)

 

 

 

 

ХОД УРОКА.

 

Подготовка к уроку:     (Подготовить мини памятки по диаграммам.

Для ознакомления учеников с табличным процессор Excel проводились  дополнительные уроки.)

 

1. Организационно-психологическая часть.

Учитель математики:

Приветствие учащихся. Начать сегодняшний урок я решила со слов: «Достижение успешного результата во время решения задач - совсем не привилегия одной математики. Вся человеческая жизнь – это ни что иное, как постоянная постановка и желание достичь успеха во время решения всё новых вопросов и проблем »

Со школы мы должны вынести не только багаж теоретических знаний и практических умений ,но и некоторые рецепты достижения успехов. Поэтому мы предлагаем вам поработать не только с математическим материалом ,но и ответить на вопрос –что именно поможет вам достичь успеха, и пополнить свой жизненный опыт по теме урока.

 

2. Подготовка к сознательной обучающей работе: постановка целей, мотивация.

Учитель математики:

Достичь успеха можно только тогда ,когда есть определенная цель. Ознакомить учащихся с планом урока и сформулировать цель.

Приготовим наши тетради к работе. Хочется напомнить ,что во время работы с деловыми документами залогом успеха есть аккуратное ,внимательное отношение к своей работе .(запись даты и темы урока) .

Для создания позитивной мотивации используем как можно больше фактического материала: виды разных диаграмм с помощью  презентации на ПК «В мире диаграмм» (прилагается на диске № 2, файл «Мир диаграмм»)

Наводим учащихся на мысль, что во-первых они должны научиться «читать» диаграммы, во вторых ,нужно научиться самим строить диаграммы ,чтоб показать наглядное соотношение между величинами.

В школьном учебнике рассматривается 2 вида диаграмм  (круговые , столбчатые). Сегодня , с помощью ПК мы увидим разнообразие форм изображения зависимости одной величины  от другой.(Презентация на ПК).

 

3.Актуализация опорных знаний.

Учитель математики:

-А где в жизни вы встречались с диаграммами и какими видами?

Ученики приводят  свои примеры.

Таким образом вы видите, что много информации можно предоставить с помощью диаграмм.

Предлагается посмотреть на отдельной доске творческие задания учащихся с составленными задачами и построенными к ним диаграммами.

В докладах своих товарищей вы часто сталкивались с понятием проценты.

-Что вы знаете об этом понятии?

Ученики дают ответ на вопрос.

Учитель информатики:

Сегодня мы будем работать на компьютере не посредственно в программе Excel. Для это повторим некоторые понятия.

1. Как запустить Табличный процессор Excel?  

     (главное меню Пуск / Все программы / Microsoft Office / Microsoft Office Excel)

2. Как открыть файл? (два раза нажать на левую клавишу мышки)
3. Как построить диаграмму?  (на панели инструментов выбрать значок диаграммы)
4. Как сохранить созданный файл? (меню Файл / Сохранить как…)

 

4. Обобщение знаний и умений.

Учитель математики:  -Сейчас мы с вами  построим диаграмму к задаче и ответим на  вопросы.

Задача 1

Построить  Столбчатую диаграмму по использованию учеником 6-Г класса Петей Ивановым свободного от учебы времени, определив процент пребывания на свежем воздухе. Если он тратит на просмотр телевизора 35%

Занятие спортом -15%

Помощь родителям -2%

Чтение литературы-19%

Игра на компьютере-25%

Пребывание на свежем воздухе (100-(35+15+2+19+25))=4%

Вопросы :

1.Сколько процентов свободного времени он проводит с пользой для здоровья? (15+4=19%)

2.Во сколько раз больше он тратит на просмотр телевизора и игры на компьютере, чем на помощь родителям?  ((35+25):2 =30 раз )

3.На что он больше (меньше) всего тратит время?

4.Что бы вы посоветовали Пете изменить в распределении свободного времени?

Задание от Мудрой Совы

Задача 2.

Из 120 грузовиков автопарка 40 автомобилей КАМАЗ (К)

60-ЗИЛ (З), остальные  ГАЗ (Г). выполнив необходимые вычисления, выясните , какая из приведенных диаграмм соответствует условию задачи?

 

 

 

 

 

 

 

Задача 3

В семье Петренков 45% -семейного бюджета составляет заработная плата отца,

30%- зарплата мамы,20%-пенсия бабушки и остаток 140гр-стипендия сына. Какой семейный бюджет Петренков? Построить столбчатую (1вариант)и коническую (2вариант) диаграммы.

 

Решение:

1)Найдём  сколько процентов составляет стипендия сына.

100-(45+30+20)=5%

2)5%-140гр                              х=140:5*100=2800 гр

  100%-хгр;       

Ответ: Бюджет семьи составляет 2800гр

 

 

5.Систематизация знаний и умений

(Вовремя выполнения практической работы ученикам даются жетоны. По количеству, которых в конце урока ученики смогут проанализировать свои умения и навыки работы с разными видами диаграмм: построение, чтение,  редактирование и форматирование.)

 

Учитель информатики

Чтобы на сегодняшнем уроке каждый мог с уверенностью сказать ,что он достиг успеха необходимо поработать над выполнением практических заданий и самостоятельно.

Китайская мудрость говорит : «… покажи мне -и я запомню , дай мне действовать самому -и я научусь…»

Умение работать самостоятельно есть важным и в учёбе и в жизни, поэтому  на этом этапе нашего урока мы не только систематизируем достижения ,но и  будем продолжать  развивать умения работать самостоятельно. Для достижения успеха важным есть наличие друзей, партнеров поэтому практическую работу проводим в парах.

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРАКТИЧЕСКАЯ  РАБОТА

ТЕМА: Построение диаграмм.

ЦЕЛЬ: Сформулировать умения и навыки учеников по построении диаграмм разных видов,      научиться их редактировать и форматировать.

ОБОРУДОВАНИЕ:

Персональный компьютер, прикладная программа Excel.

Задание:

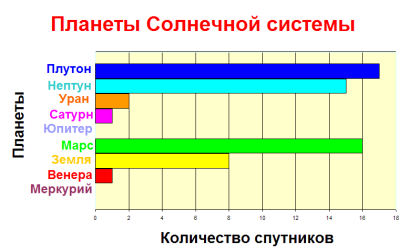В таблице показано количество спутников планет Солнечной системы. Постройте диаграмму «Планеты солнечной системы» (аналогично как показано на рисунке, прилагается на диске № 2, файл «Пример_диаграмм»), используя информацию поданную в таблице.

№	ПЛАНЕТЫ	КОЛИЧЕСТВО СПУТНИКОВ
1	Меркурий	-
2	Плутон	1
3	Нептун	8
4	Юпитер	16
5	Венера	-
6	Земля	1
7	Марс	2
8	Уран	15
9	Сатурн	17

ХОД РАБОТЫ:

Открыть документ Excel с таблицей, D:/Работа/6_класс/Диаграмма (прилагается на диске №2, файл «Диаграмма»)

Построить диаграмму (аналогично рисунку)

1. Выделить диапазон ячеек С3:С11
2. Запустить Мастер диаграмм (кнопка ).
3. Просмотреть все типы диаграмм. Выбрать – Линейная.

(Шаг 1. Выбрать тип диаграммы Линейчатая и первый вид. Нажать кнопку Далее.)

4. Установить ряды в строках.

(Шаг 2. Переключить радиокнопку Ряды в строках, в столбцах и сравнить диаграммы,            соответствующие разным представлениям ряда данных. Выбрать Ряды в строках.)

5. Дать название рядам.

(Перейдите на закладку Ряд поочереди в ячейке Имя указать названия рядов. Нажать кнопку Далее.)

6. Подписать данные, заглавия осей, название диаграммы, ось, линию сетки.

(Шаг 3. Выбрать параметры диаграммы.
Максимально возможное число закладок на этом шаге - 6.

 На каждой закладке можно определить ряд параметров диаграммы.

В закладке Заголовки, записать название диаграммы:

"Планеты солнечной системы", ось Х :  «Планеты», ось У: «Количество планет».

На закладке Оси установить флажок в поле ось У.

На закладке Линии сетки указать основные линии для оси Х.

На закладке Подписи данных установите переключатель Значение.

Нажмите кнопку Далее.)

7. Разместите диаграмму  на отдельном листе.

(Шаг 4. Выбрать для размещения диаграммы отдельный лист.

Нажать кнопку Готово.)

            8. Отформатировать диаграмму по рисунку.

9. Показать диаграмму учителю.

10. Отформатировать диаграмму по своему усмотрению, используя разные виды диаграмм.

11. Продемонстрировать работу учителю.

12. Сохранить документ под именем «Диаграмма солнечной системы»

 

Учитель информатики

Итак какие возникли трудности при выполнении практической работы?

Заслушиваются ответы учащихся.

 

Учитель информатики

Построив диаграмму мы теперь можем быстро ответить на такие вопросы:

1. У какой планеты наибольшее количество спутников?  (Сатурн)
2. Есть ли планеты, у которого нет спутников?   (Меркурий, Венера)
3. Во сколько раз у Юпитера спутников больше, чем у Нептуна?   (в 2 раза)

Сегодня мы с вами познакомились с различными видами диаграммам. Чтобы проверить на сколько вы умеете  ориентироваться в «Мире диаграмм».

Проведем с вами «Мозговой штурм».

Я говорю заглавную букву, а вы называете вид диаграмм.

Итак:

Г

– гистограмма

– график

Л

– линейчатая

– лепестковая

– логарифмическая

К

– круговая

– кольцевая

– коническая

 П

– пирамидальная

– пузырьковая

– поверхность

6. Итог урока.

Учитель математики

Мир диаграмм  многообразен и познать его за один урок не возможно. Вы еще не раз столкнетесь с ними и в школе на уроках математики в 9-11 кл., на уроках информатики в 11 кл., но и в поседневной жизни.

Сейчас настало время вернуться к началу нашего урока к цели которую мы перед собой ставили. Я считаю, что мы с вами достигли нашей цели: Выработали определенные умения и навыки работы с разными видами диаграмм: построение, чтение,  редактирование и форматирование. В начале урока мы говорили о том, что человеку помогает достигнуть успеха. Давайте попробуем проанализировать, что нам на уроке помогло достичь успеха.

 

Учитель информатики

Ответьте на вопросы:

1. Что полезного для учебы, для дальнейшей жизни вы вынесли с урока? (учились самостоятельно работать [как?], достигли успеха [как?], помогали другим, общались…)?
2. Использование компьютера помогло ли вам достичь успеха?
3. Почему мы можем сказать, что этот урок важен для нас?
4. Где, в каких ситуациях вы можете использовать полученные на этом уроке знания и умения?

 

 Оценивание:  (выставление оценок)

При оценивании учитывается и количество заработанных жетонов.

 

8. Домашнее задание.

Учитель математики:

Задача.

В селе 90 домов. Из них 15 домов под железной крышей, 45 под черепицей, остальные под шифером. Выполним вычисления, найдите сколько домов было под шифером. Изобразите на круговой диаграмме соотношение домов в зависимости от вида крыш.

(задание вы можете выполнить, используя компьютер и отчет предоставить на следующем уроке на листе А4)

 

 Учитель информатики

В любой ситуации каждый может видеть, что-то доброе и полезное. Учите свой ум и душу видеть хорошее – и тогда дорога к успеху будет для вас открыта!

Спасибо за подготовку и проведение этого урока. Желаю всем присутствующим УСПЕХА!!!

                        

                                  Підготувала:

                                                      Вчитель математики та інформатики  - Ликова І.П.

                                                      Вчитель математики – Апрасюхіна І.В.

Урок  –  лабораторна робота

 

акі уроки є однією з форм організації самостійної навчально – пізнавальної діяльності учнів. Вони дають можливість учням більш повно і свідомо з’ясувати математичні залежності між величинами, знайти певні закономірності, удосконалити навички вимірювань і обчислень, роботи з таблицями, графіками, діаграмами тощо.

Завдання лабораторної роботи вчитель записує на дошці або використовує графопроектор. Робота може складатися з обов’язкової і додаткової частин. Під час виконання завдань учні записують у зошитах тему, мету і результати виконання роботи.

Основними етапами лабораторних робіт є:

1. Актуалізація опорних знань і вмінь.
2. Мотивація навчання, повідомлення теми і мети роботи.
3. Інструктаж щодо послідовності вимірювань, обчислень, запису результатів роботи.
4. виконання учнями роботи.
5. Аналіз та оцінювання результатів роботи.

 

Наведемо приклад таких уроків – лабораторних робот.

 

Тема: „Поняття площі” (9 клас).

Мета: Безпосереднім  обчисленням  встановити та  сформувати основні властивості площі простих фігур.

 

Хід роботи.

Учням надаються малюнки простих рівних фігур. (3 трикутники, 3 чотирикутники, 3 трапеції, по дві фігури з яких рівні)

Обов’язкові завдання.

1. За допомогою лінійки виміряти відповідні сторони, та обчислити площі даних фігур. Заповнити відповідні таблиці.

Для трикутників

I                                                   II                                                 III

а1			a2			a3
h1			h2			h3
S1			S2			S3

Для прямокутників

I                                                   II                                                 III

а1			a2			a3
b1			b2			b3
S1			S2			S3

 

 

Для трапецій

I                                                   II                                                 III

а1			a2			a3
b1			b2			b3
h1			h2			h3
S1			S2			S3

Порівняти відповідні значення площ для кожного випадку фігур зробити висновок.

(Рівні фігури мають рівні площі.)

2)Учням пропонується складна фігура, яку можна розбити на декілька простих фігур. (Наприклад трапеція)

 

 

           1            2           3        

 

Завдання:

1. Визначити площу даної трапеції S.
2. Визначити площу кожної фігури, на які поділена дана трапеція S₁, S₂, S₃ . Знайти суму площ цих фігур:

S′ = S₁ + S₂ + S₃

Порівняти значення площ S та S′. Зробити висновок.

2. Аналіз виконаної роботи.

 

 

Тема: Розміщення прямої відносно системи координат (8 клас).

Мета: Сформувати поняття про розміщення прямої відносно вісей координат, якщо її рівняння ax + by + c= 0 має окремі випадки.

Хід роботи.

Обов’язкові завдання.

1. Побудувати пряму за рівнянням для випадку: а = 0, b  0, тоді у = .  Зробити висновок про розміщення прямої відносно вісі ox.
2. Побудувати пряму для випадку: b = 0, а  0;

Зробити висновок про розміщення прямої відносно вісі oy.

3. Побудувати пряму для випадку c = 0

Зробити висновок про розміщення прямої відносно системи координат.

Додаткове завдання.

Для 1 та 2 випадку побудувати пряму за умовою, що c = 0.

Зробити висновок про розміщення прямої відносно системи координат у цих випадках.

3. Аналіз виконаної роботи.

                                                 

                                                Підготувала:

  вчитель математики –  Чупікова Т.В.

 

Урок – Гра

 

Гра - це шлях дітей

до пізнання світу

в якому вони живуть

і який покликані  

зрозуміти.

 

иникнення інтересу до математики в учнів значною мірою залежить від методики її викладання, від того ,наскільки вміло буде побудована робота .

Потрібно турбуватися про те ,щоб на уроці кожний учень працював активно, захоплено і використовувати це як відправну точку для виникнення та розвитку допитливості ,глибокого пізнавального інтересу. Це особливо важливо робити у підлітковому віці ,коли ще тільки формуються, а іноді ще тільки  зароджуються постійні інтереси  і нахили до певного предмету .Саме в цей період учителю треба розкрити притягальні сторони математики .Важлива роль тут відводиться дидактичним іграм на традиційних уроках математики та урокам –іграм. Сучасна дидактика справедливо вбачає в них можливості ефективної організації взаємодії учителя і учнів, продуктивної форми їх спілкування з елементами змагання, розкутості, інтересу.

  Гра –це творчість, гра-це праця . У процесі гри у дітей формується звичка зосереджуватися, мислити самостійно, розвивається увага, уява ,прагнення до знань. Захопившись учні не помічають, що вчаться :пізнають, запам’ятовують нове , орієнтуються в незвичних ситуаціях, фантазують.

    Нетрадиційними і цікавими для учнів є урок-подорож , урок-казка . Казкові герої можуть спонукати дитину долати ті чи інші математичні труднощі.                                                           

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

гра

Брейн – ринг

„Математика-Королева Наук”

Мета:

• Перевірити рівень засвоєння матеріалу по всьому курсі математики;
• Розвивати системність мислення, пам’ять, спостережливість, логічне мислення;
• Поглибити вміння аналізувати;
• Сприяти вихованню всебічно розвиненої особистості.

План проведення:

Змагаються між собою дві команди: переможець другого туру та команда під номером 4. Тур складається з 12 запитань. Він визначає переможця брейн-рингу. Цей тур містить 16 запитань.

 

 Гра проводиться для учнів 11-х класів.  Деякі запитання з історії математики можуть здатися складними. Та нема  жодного запитання, відповідь на яке учні не чули під час вивчення відповідних тем на уроках.  

 У відбірних турах ведучому допомагають асистенти. Вони слідкують за тим, хто з капітанів двох команд, які змагаються, першим підніме руку після того, як буде зачитано запитання.

 

Щоб не було незаповнених пауз, звучить тематично підібрана музика: «2x2 = 4», «Чему учат в школе», «Песня Незнайки» та ін.

 

Ведучий:         Добрий вечір, дорогі друзі!

                          Брейн-ринг вітає вас!

Тема якого - „Математика- королева наук”.

Сьогодні ви будете свідками найцікавішої боротьби між командами. В нашому змаганні не можна вигукувати з місця, тупотіти, свистіти. Категорично забороняється підказувати.

А зараз послухаємо склад команд. Отже, починаємо наш Брейн-ринг.

Насамперед ми виберемо наше журі і асистентів, які будуть уважно спостерігати за грою і рахувати бали команд.

 

( Вибирається шановне журі та асистенти. Виходять команди починається привітання.)

Команда 1:Ми, за справедливий і чесний конкурс, в якому переможе сильніша команда і дружба.

Команда 2: Ми урочисто обіцяємо: якщо виграємо, то не задиратимемо носа, а якщо програємо – то не будемо лити гірких сліз.

Команда 3:   Щоб усе було гаразд.

            Прикладемо старання .

Виконаємо дружно ми

Ведучого всі бажання.

Команда 4: Хочемо, щоб противник наш.

Другом був завжди для нас.

(Дві команди сідають за столи. Починається гра).

 

Ведучий: Запрошуємо на сцену гравців.

1. Піфагор та його учні вважали, що «числа правлять світом». Розставте числа в порядку спадання.

 А. Тисяча.  В. Мільйон.  С. Трильйон.  D. Мільярд.

                                                                         Відповідь. С, D, В, А.

Ведучий.   

2. Чому дорівнює сума кутів рівнобедреного трикутника?

А. 180°.       В. 360°.       С. 90°.       D. 60°.

Ведучий.  

3. Багато хто з математиків були філософа­ми, геометрами, механіками, астрономами... Наприк­лад, Ісаака Ньютона, видатного англійського вченого, математики вважають математиком, фізики — фізиком, астрономи — астрономом. Джіроламо Кардано займався медициною, в математиці його ім'я носить формула для розв'язування кубічних рівнянь, а в механіці — кар­данний вал. Багато хто з математиків дружив зі спортом.

                      Хто з учених давнини був переможцем кулачних боїв?

А. Евклід.           С. Піфагор.

В. Фалес.            D. Архімед.

Ведучий.     

Так, саме Піфагор брав участь у кулачно­му бою на олімпіаді в 548 р. до н. є. і довго утримував титул чемпіона в цьому виді спорту.

Ведучий.    

4. Як називається частина круга, що містить­ся між двома  радіусами?

А. Сектор.  В. Сегмент.   С. Радіан.  D. Діаметр.

Ведучий.    

5. Хто написав перший російський підручник з математики?

А. Лобачевський.          С. Магницький.

В. Ковалевська.             D. Колмогоров.

Ведучий.  

Так, саме Леонтій Магницький у 1703 р. написав цей підручник і назвав його «Арифметика». Михайло Ломоносов називав цю книгу «вратами своєї вченості» і майже всю її знав напам'ять.

Ведучий.  

6. Які лінії перетинаються у центрі вписано­го кола?

А. Висоти.          С. Бісектриси.

В. Медіани.        D. Серединні перпендикуляри.

Ведучий.     

7. Кого називають «батьком алгебри»?

А. Евкліда.     В. Вієта.      С. Декарта.     D. Гаусса.

 

 

Ведучий.      Так, це Франсуа Вієт, французький уче­ний, за освітою юрист. Зацікавився астрономією, для цього йому були потрібні знання з алгебри і тригоно­метрії. Він почав вивчати математику, щоб написати великий астрономічний трактат. Та математика, як ви­явилося, ховала не менше загадок, ніж космос, їх вис­тачило на все життя. Трактат з астрономії не був напи­саний, а математика завдяки Вієту зробила великий крок у своєму розвитку. Саме Вієт першим почав позначати буквами не лише невідомі, а й коефіцієнти при них, що дало можливість виражати властивості рівнянь та їх коренів загальними формулами. За це Вієта й назва­ли «батьком алгебри». Одна з теорем алгебри носить його ім'я.

Ведучий.   

8. Що таке орт?

А. Одиничний вектор.       С. Вісь ординат.

В. Вісь абсцис.                      D. Один із телевізійних каналів.

Ведучий.    

9.  Що таке аргумент?

А. Музичний інструмент.

В. Вісь Ох.

С. Незалежна змінна.

D. Залежна змінна.

Ведучий.

Так, аргумент — це незалежна змінна. Поняття змінної величини ввів Рене Декарт у книзі «Геометрія» більш ніж 300 років тому.

 

Ведучий.

10. Фігури називаються рівновеликими, якщо вони мають однакові.

                      А. Сторони.   В. Кути.   С. Периметри.    D. Площі.

Ведучий.    

11.  S =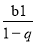— формула для обчислення...

А. Площі сектора.

В. Суми арифметичної прогресії.

С. Суми геометричної прогресії.

D. Суми нескінченно спадної геометричної прогресії.

Ведучий.   

12. Графіком функції у² - х = 0 є...

                     А. Коло.

                     В. Парабола симетрична відносно осі Ох

                     С. Парабола симетрична відносно осі Оу.

                     D. Пряма.

Ведучий.

13. Алгебра тримається на чотирьох китах: число, рівняння, тотожність, функція. З прикладами функціональних залежностей людство зустрічалося з давніх-давен. А саме слово «функція» вперше застосу­вав Готфрід Лейбніц у XVII ст. Воно походить від ла­тинського “functio”.Що в перекладі означає це слово?

А. Відновлення.           С. Рух.

В. Виконання.              D. Залежність.

Ведучий.    

14. Піфагор багатьом числам дав назви.

                      Як він назвав числа, у яких сума дільників одного з них                        дорівнює другому числу?

А. Досконалими.          С. Фігурними.

В. Дружніми.                D. Близнюками.

 

Ведучий. Досконалим Піфагор назвав число, яке дорівнює сумі своїх дільників. До фігурних він відно­сив трикутні, квадратні та інші, які можна отримати, якщо з камінців викладати трикутник чи квадрат. Числа-близнюки, це такі числа, які йдуть одне за одним у ряду простих чисел. Розглядалися чоловічі та жіночі числа тощо. А пари чисел, про які йшлося у запитанні, Піфагор назвав дружніми.

 

Ведучий. 

15. Як відомо, геометрію побудовано аксіо­матично. А чи можна аксіоматично побудувати алгеб­ру? Над цим питанням замислились у кінці XIX ст.

Хто з математиків побудував систему аксіом для дійсних чисел?

А. Пеано.      В. Абель.      С. Галуа.      D. Дедекінд.

Ведучий:

16. З давніх-давен щасливим вважалося число 7. У бага­тьох народів це число увійшло до легенд, прислів'їв та приказок. Усі чули про 7 чудес світу.

                      Хто може їх назвати?                                   

      Відповідь:

1.  Висячі сади Семіраміди у Вавилоні.

2.  Піраміди у Єгипті.

3.  Храм Артеміди в Ефесі.

4.  Статуя Зевса в Олімпії.

5.  Гелікарнаський мавзолей.

6.  Статуя Бога Сонця на острові Родос (колос Ро­доський).

7.  Александрійський маяк.

 

Ведучий: Поки ми проведемо хвилинку відпочинку, журі порахує бали і скаже переможця.

(Один із болільників розповідає віршик)              

Проста арифметика.

Викликає вчитель Люду,

Слабшу серед дітвори,

І питає: «Скільки буде:

Десять поділить на три?»

Розв'язать вона не може,

Звісно, знітилась, мовчить...

Вчитель каже: «Так не гоже.

Прості дроби треба вчить».

«Хай картоплі є десяток, —

Вчитель далі річ веде, —

Розділи на трьох дівчаток.

То по скільки припаде?»

Люда каже: «Зайвий клопіт,

І нащо мені це знать?

Я зварю їм ту картоплю,

Потовчу — і хай їдять...»

А.Динник.

 

(Журі називає переможця.)

 

Ведучий.   Вітаємо всіх везунчиків з перемогою! Нехай і надалі вам щастить!

 

 

 

                                 Підготувала:

                                                      Вчитель математики та інформатики  - Ликова І.П.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок – захист учнями творчих робіт

 

 Необхідний час – 90 хвилин.

    Підготовка до уроку триває до двох тижнів. Оголошується тема, дається список рекомендованої літератури, визначається термін  написання робіт та дата їх перевірки. Протягом усього часу вчитель проводить консультації і допомагає визначитися з рекомендованою літературою, розібратися з більш складним теоретичним матеріалом, пояснює, переглядає та коректує роботи, відбирає найбільш вдалі.

    Тема: Декартові координати на площині.

    Мета: формувати уміння застосовувати здобуті знання у нестандартних                  умовах; вчити їх аналізувати та систематизувати ті знання, які вони отримують на уроках і черпають з додаткової літератури.

  

 Напис на дошці:

    Каждая решенная мною задача становилась образцом, который служил впоследствии для решения других задач.

                                                                                                                           Р. Декарт

Хід уроку

І. Актуалізація опорних знань.

            ( у формі бесіди )

Запитання для бесіди

1. Пояснити, як знаходяться координати точки.
2. Які знаки мають координати точки в кожній чверті?
3. Записати формули для координат середини відрізка.
4. Записати формулу для відстані між точками.
5. Записати рівняння кола.
6. Як знайти координати точки перетину двох прямих, які задані рівнянням цих прямих.
7.  Що таке кутовий коефіцієнт  прямої і який його геометричний зміст?
8. При якій умові пряма і коло не перетинаються, перетинаються в двох точках, дотинаються?
9. Дати поняття синуса, косинуса, тангенса для довільного кута від 0⁰ до 180⁰.

 ІІ. Повідомлення теми та мети уроку.

   Оголошуються приз віща доповідачів та порядок їх виступів.

ІІІ. Творче застосування узагальнених знань, навичок та умінь.     

    Доповідачі виступають зі своїми повідомленнями. У кінці кожного виступу учні задають доповідачу запитання.

1. Загальна характеристика епохи.
2. Коротка біографія Р. Декарта.
3. Гносеологія нового часу.
4. Рене  Декарт і його внесок в теорію пізнання.
5. Критика вчення Декарта Локкартом і Юмом.
6. Значення вчення Декарта.
7. Декартова система координат.

1. Общая характеристика эпохи.

    Гносеология – теория познания, - по Н. Гартману, метафизическая составная часть познания наряду с логической и психологической.

    Теория познания – сердце и души философии в том виде, в котором она существовала с начала XVII века. Большинство самых крупных философов – Р. Декарт, Г. Лейбниц, Дж. Локк, Д. Беркли, Дэвид Юм, Иммануил Кант _ сделали эпистемологические исследования главной части своей работы. Если мы не можем осознать, что заставило их столь серьёзно заняться вопросами, которые кажутся нам странными сегодня, то мы не можем действительно понять философию в том виде, в котором она существовала в течении последних четырёх веков. Во – вторых, кажущиеся странными проблемы современной теории познания непосредственно связаны с одной из ведущих культурных и интеллектуальных черт развития постсредневекового мира, а именно, с устойчивым движением к радикальному индивидуализму в религии, политике, искусстве и литературе, а также философии. Хотя эпистемологические загадки философии XVII – XVIII веков кажутся на первый взгляд странными и не имеющими отношения к интуиции, но они оказали глубокое влияние на то, как рисовали художники, писали поэты, каким образом теологи интерпретировали “ Слово Божье “, и даже на те способы, которыми экономисты, политологи и социологи объясняли нашу коллективную социальную жизнь.

2. Краткая биография Р. Декарта.

    По общему признанию, человеком, который открыл новую страницу в теории познания, был француз Рене Декарт, родившийся в 1596 г. в Лаэ (Турень, Франция). Происходил из старинного дворянского рода. Образование получил в иезуитской школе Ла Флеш в Анжу. В начале 30 – летней войны служил в армии, которую оставил в 1621 г.; после нескольких лет путешествий переселился в Нидерланды, где провел 20 лет в уединенных научных занятиях. Здесь вышли его главные сочинения. В 1649 г. По приглашению шведской королевы Кристины переселился в Стокгольм, где вскоре умер в 1650 г.

 Хотя Декарт за 54 года своей жизни написал ряд значительных работ, в которых обсуждались проблемы математики, физики и других наук, в том числе и философии, мы можем точно назвать философскую работу, которая знаменует собой начало современной философии в том её виде, в котором мы её изучаем сегодня. Это – “размышления о первой философии”, опубликованные Декартом в 1641 г. (русский перевод 1950 г.). следует отметить, что XVII век был веком научных гигантов, но среди великих мыслителей познания, усилиями которых было создано то , что известно сегодня как современная наука, только немец Готфрид  Лейбниц и англичанин Иссак Ньютон могут встать рядом с Декартом.

 

3. Гносеология нового времени: рационализм и эмпиризм.

Декарт родился три четверти века спустя после того, как Мартин Лютер начал протестантскую реформацию, прибив гвоздями свои знаменитые тезисы к дверям церкви в Виттенберге. Любопытно, что сам Декарт был и всю свою жизнь оставался католиком. Своё начальное образование, как отмечено выше, философ получил у иезуитов. Однако если сущностью протестантской Реформации был отказ от религиозной власти института церкви и акцент на первичность индивидуального сознания, то ясно, что Декарт был интеллектуально и эмоционально крайним протестантом. Ведущей нотой его работы на протяжении всей жизни был бескомпромиссный отказ от общепринятого мнения, установившейся дактрины и власти, предшественников, а также совершенно индивидуалистическое требование приятия только тех истин, которые его собственный разум может признать доказательным.

Когда ему было едва за 20 лет, интерес Декарта был обращен к математике и физике – областям, в которых в то время доминировали еще аристотелевские и платоновские концепции и методы почти двухтысячелетней давности. Новые, захватывающие открытия были сделаны в обеих областях и Декарт, как и многие молодые гении, устремился в эту сферу. В ночь на 10 ноября 1619 года Декарт увидел три сна, которые перевернули всю его жизнь. Он говорил и писал о них впоследствии, как о поворотной точке своей карьеры. Сам Декарт интерпретировал свои сны как знак того, что он должен посвятить свою жизнь открытию новой объединённой теории Вселенной, основанной на математике – то, что сегодня можно было бы назвать математической физикой.

 

4. Выдающиеся мыслители: Рене Декарт и его вклад в теорию познания.

В круге вопросов философии, которые разрабатывал Декарт, первостепенное значение имел вопрос о методе познания. Как и Ф. Бэкон, Декарт видел конечную задачу знания в господстве человека над силами природы, в открытии и изобретении технических средств, познании причины действий, в усовершенствовании самой природы человека. Декарт ищет, безусловно, достоверное исходное основоположение для всего познания и метод, посредством которого возможно, опираясь на это основоположение, построить столь же достоверное знание всей науки. Ни это основоположение, ни этого метода он не находит в схоластике. Поэтому исходный пункт философских рассуждений Декарта – сомнение в истенности общепризнанного знания, охватывающего все виды знания. Однако, как и у Бэкона, сомнение, с которого начинал Декарт, есть не убеждение агностика, а только предварительный методический приём. Можно сомневаться в том,  существует ли внешний мир, и даже в том, существует ли моё тело, но само моё сомнение, во всяком случае, существует. Сомнение же есть один из актов мышления. Я сомневаюсь, поскольку я мыслю. Если, таким образом, сомнение – достоверный факт, то оно существует лишь, поскольку существует мышление, поскольку существую я сам в качестве мыслящего: «… Я мыслю, следовательно, я существую…».

В учении о познании Декарт был родоначальником рационализма, который сложился в результате наблюдения над логическим характером математического знания. Математические истины, по Декарту, совершенно достоверны, обладают всеобщностью и необходимостью, вытекающими из природы самого интеллекта. Поэтому Декарт отвёл заключительную роль в процессе познания дедукции, под которой он понимал рассуждения, опирающиеся на вполне достоверные исходные положения (аксиомы) и состоящие из цепи также достоверных логических выводов. Достоверность аксиом усматривается разумом интуитивно, с полной ясностью и отчётливостью. Для ясного и отчётливого представления всей цепи звеньев дедукции нужна сила памяти. Поэтому непосредственно очевидные исходные положения, или интуиция, имеют преимущество сравнительно с рассуждениями дедукции. Вооруженный достоверными средствами мышления – интуицией и дедукцией, разум может достигнуть во всех областях знания полной достоверности, если только будет руководствоваться истинным методом.

Таким образом, важной частью плана Декарта является не новая наука, которую он разработал, а его концепция методов, с помощью которых он должен был проводить исследования. В своей частично биографической, частично философской работе, вышедшей в свет в 1637г. и озаглавленной «Рассуждения о методе, чтобы верно направлять свой разум и отыскивать истину в науках», он излагает четыре правила, которые, как он утверждает, являются достаточными для того, чтобы направлять свой разум:

«Первое – ни когда не принимать за истинное ничего, что я не признал бы таковым с очевидностью, то есть тщательно избегать поспешности предубеждения и включать в свои рассуждения только то, что предоставляется моему уму столь ясно и отчётливо, что никому никаким образом не может дать повод к сомнению (т.е. допускать в качестве истинных только такие положения, которые представляются истинными и отчётливыми, не могут вызвать никаких сомнений в их истинности).

Второе – делить каждую из рассматриваемых мною трудностей на столько частей, сколько потребуется, чтобы лучше их разрешить (т.е. расчленять каждую сложную проблему на составляющие её частные проблемы или задачи).

Третье – располагать свои мысли в определённом порядке, начиная с предметов простейших и легко познаваемых, и восходить мало помалу, как по ступеням, до познания наиболее сложных, допуская существование порядка даже среди тех, которые в естественном ходе вещей не предшествуют друг другу (т.е. методически переходить от известного и доказанного к неизвестному и недоказанному).

И последнее – делать всюду перечни настолько полные и обзоры столь всеохватывающие, чтобы быть уверенным, что ничего не пропущено» (т.е. не допускать никаких пропусков в логических звеньях исследования).

Прежде всего, метод Декарта – это метод вопрошания. Другими словами – это метод доказательства того, что вы уже знаете, или усовершенствование вашего знания путём его систематизации. Правила для ума Декарта должны послужить руководством для человека, который пытается разрешить какую-либо проблему или проанализировать какое-либо явление. Другими словами, он принимает точку зрения человек, который ещё не знает нечто, но пытается открыть это нечто с помощью своего ума, а не исходя из точки зрения учителя или эксперта, которые совершенно уверены в том, что они знают нечто, и просто пытаются объяснить это кому-нибудь ещё.

Во-вторых, метод Декарта – это метод сомнения. Его первое правило: «никогда не принимать за истинное ничего, что я не признал бы таковым с очевидностью». Декарт имеет в виду, что мы должны отказываться принимать нечто, как бы до этого ни были уверены в том, как бы много людей не верило в это, сколько бы очевидным это ни казалось до тех пор, пока мы не сможем быть абсолютно уверенными в том, что это на 100% верно. Если же существует малейшее, самое смутное, самое слабое сомнение относительно истинности подобного факта, то мы не должны его принимать.

Когда метод вопрошания комбинируется с методом сомнения, начинается трансформация самой природы философии. Эта трансформация, называемая некоторыми эпистемологическим поворотом, потребовала для своего завершения полтора века, вплоть до кантовской «критики чистого разума». После этого вся философия настолько изменилась, что сами вопросы, которые философы ставили, а также ответы, которые они давали, очень мало походили на то, что было написано до «Размышлений…». Эпистемологический поворот – очень простое , но хитрое понятие.

Сердцем епистемологического поворота не более, чем обращение назад в постановке двух основных вопросов философии. Со времён первых до сократовских космологов до эпохи Декарта на первое место философы ставили вопросы о том, что существует, о природе Вселенной, и только потом вопрошали о том, что я могу узнать относительно того, какова природа Вселенной. Это означает, что философы считали, что вопросы бытия имеют превосходство и они важнее вопросов сознания. Таким образом, в философии, которая предшествовала Декарту, метафизика брала верх над эпистемологией.

Два метода Декарта – метод вопрошания и метод сомнения – результат пересмотра предшествующего положения вещей. Понятые в прямом смысле слова и проводимые с последовательностью и твёрдостью, которых сам Декарт никогда не достигал, эти два метода заставили философов отложить вопросы бытия до тех пор, пока они не разрешат вопрос познания. А сам этот факт изменения значения вопросов о бытии так, что ко времени, когда революция, начатая Декартом, пошла своим ходом, привёл к тому, что метафизика старого типа закончила своё существование, а эпистемология нового типа заняла её место в качестве основной философии.

Как упоминалось выше, когда Декарт резюмировал доказательства своего собственного бытия на латинском языке, он употреблял фразу: «Cogito, ergo sum», что означает «Я мыслю, следовательно, существую». Таким образом, его доказательство стало известным в философском обиходе как Cogito – аргумент. Произнесение или утверждение высказывания является решающим моментом, потому что именно утверждение гарантирует истинность. Суть состоит в том, что если высказывание утверждается, то кто-то должен совершать это утверждение и, если я утверждаю его, этот кто-то должен быть мною. Нет необходимости говорить, что я не могу использовать это доказательство для утверждения существования кого-либо ещё. Моё утверждение всякого высказывания, истинного или ложного относительно меня самого или относительно кого-либо ещё, гарантирует, что я существую, потому что я есть субъект (т.е. тот, кто утверждает, т.е. сознательно мыслит это высказывание). А это есть ключевой момент – высказывание есть утверждение, и, следовательно, оно должно быть утверждаемо кем-то.

В своём первом «Размышлении…» Декарт сомневается во всём, что не известно с достоверностью. Он доходит до того, что принимает такой строгий критерий достоверности, что, в конечном счёте, ничто, кроме утверждения о его собственном существовании, не может удовлетворить его требованиям. Рассматривая всё многообразие своих верований, Декарт далее разделяет их на две большие группы: те верования, которые, как он считал, ему известны на основании свидетельств его собственных чувств, и те верования, которые, как он полагал, известны ему на основании мышления с помощью общих понятий.

Таким образом, благодаря аргументации в первом «Размышлении…» Декартом поднимаются две главные проблемы. Первая – это проблема достоверности. Какой критерий истинности мы должны принять в качестве стандарта, с которым соотносим наши познания? Вторая проблема есть источников познания. Если мы что-либо знаем, то встаёт вопрос о том, основано ли наше знание на источниках чувств, на абстрактном размышлении, или на некоей комбинации их обоих? Философия последующих 150 лет после опубликования «Размышлений…» представляла собой различные вариации этих двух главных тем.

Сам Декарт предложил предварительные ответы на вопросы о достоверности и источниках познания в заключительной части второго «Размышления…». В отношении проблемы достоверности он предложил два критерия, две проверки достоверности размышления:

1. «… ясное и чёткое ощущение того, что я произвожу высказывание, чего в действительности было бы недостаточно для того, чтобы убедить меня в том, что то что я говорю, истинно».
2. «… все вещи, которые я ощущаю, совершенно ясно и отчётливо, являются истинными».

Что касается источников нашего знания, то Декарт честно и прямо становится на сторону разума, а не на сторону чувств. Это именно то, чего и следовало ожидать от того, кто мечтал создать математическую физику. Вместо наблюдения и собирания данных на основе зрения, слуха, обоняния и осязания Декарт предпочитает создавать универсальную систему науки, исходя из логических и математических предпосылок и обоснованную жёсткой дедукцией. Чтобы убедить своих читателей в первичности разума в процессе познания, Декарт использует то, что называется «мыслительным экспериментом». Другими словами, он просит нас вообразить вместе с ним некую ситуацию (в данном случае то, что он сидит около камина с куском воска в руке), и затем он пытается нас заставить увидеть благодаря анализу ситуации, что наши методы рассуждения и познания должны иметь достоверный характер. Философы часто прибегают к такого рода утверждениям, когда они пытаются установить некоторые общие высказывания, а не доказывать определённый факт. В современной науке считается, что мысленный эксперимент не может выступать в качестве доказательства. В действительности он скорее является простым инструментом исследования логических и концептуальных взаимоотношений между различными идеями, так как должен дополняться тщательными вычислениями.

5. Критика учения Декарта Локкартом и Юмом.

Дискуссия по декартовым проблемам вскоре сама вылилась в конфликт между двумя более или менее сложившимися школами мысли – рационалистами и эмпириками.

Рационалисты приняли требования Декарта о неопределённости, они согласны с его точкой зрения на то, что логика и математика являются моделями для всякого истинного знания, и стараются отыскать способы построения главных утверждений науки и метафизики, обладающие той же степенью определённости и истинности, как силлогизм и геометрия. Они изыскивают доказательства существования Бога; они демонстрируют в качестве наглядных примеров фундаментальные принципы новой физики и продолжают верить в мечту Декарта о создании универсальной системы знания. Так же, как и Декарт, они отрицают значение наших чувств как источника знания и вместо этого выдвигают требования, чтобы всё истинное знание основывалось на операциях разума.

Эмпирики также принимают стремление Декарта к достоверности, но всё более настойчиво атакуя позицию рационалистов, они утверждают, что это требование не может быть выполнено. Дэвид Юм, наиболее блестящий и выдающийся представитель эмпириков, самым убедительным образом показал, что не утверждения науки, ни верования здравого смысла не могли бы, вероятно быть квалифицированы как знание, если рассматривать их с точки зрения собственно декартовых стандартов достоверности.

Эмпирики отвергают также и приверженность рационалистов к разуму, как единственному источнику познания. Сначала Джон Локк в своём «Трактате о человеческом понимании», а затем Юм «Трактате о человеческой природе» настаивали на том, что все идеи, содержащиеся в человеческом разуме, должны в конечном счёте проистекать из зрения, слуха, обоняния, осязания и вкуса, присущих нашим органам чувств. Разум, утверждают они, в действительности может сделать не больше, чем организовать и отсеять тот материал, который он получает через ощущения. Это подчинение разума чувствам было одним из самых сильных аргументов в наступлении эмпиристов на научные и метафизические системы, которые выдвигались философами – рационалистами.

Последовательно рассматривая возражение философов – эмпиристов «Размышление…» Декарта, следует начать с наступления, предпринятого Локком. Локк воспользовался простой, но очень действенной стратегией для своей атаки на утверждение, что только разум может дать нам знания. Вместо того, чтобы исследовать наши требования к познанию непосредственно, Локк предлагает задаться вопросом о том, из какого источника мы берём идеи, которые используем, устанавливая эти требования к познанию.

Согласно Локку, наш разум в момент нашего рождения представляет собой пустое свободное место. Он сравнивает его с листом чистой бумаги, на котором опыт пишет свои письмена. Согласно Локку: «…представим себе, что разум есть, как мы выражаемся, чистая бумага, лишённая всяких образов, всяких идей. Каким же образом он заполняется? Откуда берутся эти обширные запасы? Откуда берётся весь этот материал разума и познания? На это я отвечаю одним словом – опыт. В нём одном находится основание всего нашего познания; и из него, в конечном счёте, происходит всё».

Эмпириком, который довёл стратегию Локка до её логического конца, был Дэвид Юм. На самых первых страницах «Трактата о человеческой природе» Юм заимствует стратегию Локка и выдвигает свою версию принципа «белой бумаги». Он использует слово «восприятие» для того, чтобы обозначить любое содержание разума, и затем разделяет восприятия на те, которые происходят прямо из наших чувств, и на те, которые мы образуем на основе наших впечатлений, воспроизводя, классифицируя или же, в противном случае, изменяя их.

В теории Юма следует отметить три ключевых момента:

1. это, конечно, то, что Юм принял теорию «белой бумаги»;
2. это то, что иногда называют теорией идей – копий. Согласно Юму все наши идеи являются либо прямыми копиями чувственных впечатлений, либо комбинациями и перестановками копий чувственных впечатлений;
3. то, что у Юма имеется «атомистическая» теория содержания разума. Это означает, что он мыслит разум, как состоящий из маленьких неделимых «атомарных» кусочков ощущений и из неделимых копий этих кусочков, и ещё из того, что мы могли бы назвать «молекулярными» комбинациями атомарных ощущений.

Поскольку всё содержание разума может быть разделено на атомарные единицы, то из этого следует, что мы всегда можем отделить одну единицу от другой. Кроме того, говорит Юм, разум имеет власть разделять две единицы ощущения друг от друга, представляя одну из них несуществующей, и в то же время сохраняя другую в разуме. Посредством этих двух принципов, которые прямо следуют из его теории идеи, как копий, и из его атомарной теории содержания разума, Юм делает вывод, который одним махом сметает все метафизические, все естественнонаучные и почти все наши верования о мире, обоснованные здравым смыслом: «…опрометчиво поступают те, кто говорит, что всякое действие должно иметь причину, потому что последняя заключена в самой идее действия. Всякое действие необходимо изменяет причину, так как действие – относительный термин, коррелятом которого является причина. Но не доказывает, что каждому бытию должна предшествовать причина, точно так же, как из того, что каждый муж должен иметь жену ещё не следует, что каждый мужчина должен оказаться женатым. Правильная постановка вопроса такова: всякий ли объект, начинающий существовать, обязан своим существованием какой-нибудь причине? Я утверждаю, что это не достоверно, не интуитивно, не демонстративно и надеюсь, что такое мнение в достаточной степени было доказано мной с помощью предшествующих аргументов».

Не надо обладать богатым воображением, чтобы понять глубину выводов Юма. Я верю, что когда я сделаю глоток воды, это уменьшит испытуемую мною жажду. Я верю, что когда я поверну выключатель, загорится свет. Простейшие утверждения химии, физики и биологии, либо сами являются причинными суждениями, либо зависят от последних.

6. Значение дуалистичности учения Декарта для последующего развития идеализма и материализма.

Таким образом, можно отметить, что британские эмпирики сделали выводы из скептических аргументов Декарта более последовательно, чем он это сделал сам, и, таким образом, поставили под вопрос в отношении единства и существования личности, основные утверждения физики и математики. Продолжавшееся до середины XVIII века сражение эмпириков и рационалистов без решающего успеха какой-либо стороны были остановлены вышедшей в 1781г. работой немецкого философа Иммануила Канта «Критика чистого разума», изменившей понимание познания, сознания, собственной личности и отношения между тем, что мы знаем, и способом, каким существуют вещи.

Учение Декарта и направление философии и естествознания, продолжавшее его идеи, получило название картезианство (латинизированное имя – Картезий), он оказал значительное влияние на последующее развитие науки и философии. Учение Декарта о непосредственной достоверности самосознания, о врождённых идеях, об интуитивном характере аксиом, о противоположности материального и идеального явились опорой для развития идеализма. С другой стороны, учение Декарта о природе и его всеобщий механистический метод делают философию Декарта одним из этапов материалистического мировоззрения нового времени.

7. Декартова система координат.

    Декартова  система координат – прямолинейная система  координат в евклидовом пространстве.

    На плоскости общая декартова система координат ( аффинная система координат ) задаётся точкой О ( начало координат ) и упорядоченной парой приложенных к ней неколлинеарных векторов L₁ и L₂ (базисных векторов). Прямые, проходящие через начало координат в направлении базисных векторов, называются  осями координат данной Д. с. к. Первая, определяемая вектором L₁, называется осью абсцисс (или осью Ох),вторая осью ординат (или осью Оу). Сама Д. с. к. обозначается О_L1L2 или Оху. Декартовыми координатами точки М (рис. 1) в Д. с. к. О_L1L2 называется упорядоченная пара чисел (х, у), которые являются коэффициентами разложения вектора ОМ  по базису L₁L₂:

OM = XL₁+XL₂

    Число х называется абсциссой, число y – ординатой точки М. Если (x,y)- координаты точки М, то пишут М (x,y).

    Если на плоскости введены две Д. с.к. ОL₁L₂ и О^/L^/₁L^/₂ так, что векторы базиса L^/₁L^/₂выражены через векторы базиса L₁L₂ формулами

L^/₁= A₁₁L₁ + A₁₂L₂,

L^/₂ = A₂₁L₁ + A₂₂L₂

 и точка О^/ имеет в Д. с. к. ОL₁L₂ координаты (х, y) точка М в Д.с.к. ОL₁L₂ и координаты (x, y) той же точки в Д.с.к. О^/L^/₁L^/₂связаны соотношениями

X = A₁₁X^/ + A₂₁Y^/ + X_0,

Y = A₁₂X^/ + A₂₂Y^/ + Y₀

    Д.с.к. называется прямоугольной (прямоугольной системой координат), если базис L₁L₂ – ортонормированный, т.е. векторы L₁и L₂ взаимно перпендикулярны и по длине равны единице (векторы L₁ и L₂ называются в этом случае ортами). В прямоугольной Д.с.к. координаты (х, у) точки М (прямоугольные координаты) соответственно равны: х – величине ортогональной проекции вектора ОМ  на ось абсцисс, у – величине ортогональной проекции вектора ОМ на ось координат. В прямоугольной Д.с.к. Оху расстояние между точками М₁(х₁,у₁) и М₂ (х₂, у₂) равно:

М₁ М₂ = (х₁ – х₂)² + (у₂ – у₁)²

    Формулы перехода от одной прямоугольной Д.с.к. Оху к другой прямоугольной Д.с.к. О^/x^/y^/, начало которой О^/ имеет в Д.с.к. Оху координаты (х₀,у₀), имеет вид:

 

Х = Х^/COSL – Y^/SINL + X₀,

Y = X^/SINL + Y^/COSL + Y₀.

Или

X = X^/COSL + Y^/SINL + X₀,

Y = X^/SINL – Y^/COSL + Y₀.

    В первом случае система Оx^/y^/ образуется поворотом базисных векторов на угол L и последующим переносом начала координат в точку О^/ (рис. 2), а во втором случае – поворотом и последующим отражением относительно прямой, несущей вектор L₁, а затем переносом начала координат (рис. 3).

    Иногда используется косоугольная Д.с.к., отличающаяся от прямоугольной тем, что угол между единичными базисными векторами не являются прямыми.

    Аналогично определяется общая декартова система координат (аффинная система координат) в пространстве заданием точки О – начала координат, и базисных векторов – трёх некомпланарных векторов L₁, L₂, L₃. аналогично плоскому случаю (рис.4) определяются оси координат – ось абсцисс  (или ось Ох), ось ординат (или ось Оу) и ось аппликат (или ось Оz). Д.с.к. в пространстве обозначается О_L1L2L3 (или ось Oxyz).

    Плоскости, проходящие через пару осей координат, называются координатными плоскостями. Д.с.к. в пространстве называется правой, если поворот от оси Ох к оси Оу совершается в направлении, противоположном часовой стрелке, если смотреть на плоскость Оху из какой-нибудь точки положительной полуоси Оz, в противоположном случае – левой. Если базисные векторы L₁,L₂,L₃ единичной длины и попарно перпендикулярны, Д.с.к. называются прямоугольной (прямоугольной системой координат). Положение одной прямоугольной Д.с.к. с той же ориентацией определяется тремя эйлеровыми углами.

    Д.с.к. названа по имени Р.Декарта, хотя в его соч. “ Геометрия ” (1637) система координат сводилась к оси абсцисс с началом отсчёта и системе параллельных, вообще говоря, наклонных ординат, а расстояния по оси и до оси могли быть только положительными числами. Но в издании 1659 – 61 к “ Геометрии “ приложена работа И. Гудде, в которой впервые допускаются как положительные, так и отрицательные значения координат.

    Пространственную Д.с.к. ввёл Ф. Лаир (1679); он же впервые применил термин “ начало” – отсюда, видимо, обозначение О для начала координат. Обозначение х,у,z для декартовых координат не были приняты сразу и установились лишь в начале XVIII века. Современное название “ правая “ и “ левая “ системы предложены Дж. Максвеллом (1873).     

     

 

 

 у

 

 

 

 

 е₂ х

 Рис. 1

 о е₁

 

 

 у x^/

у^/

 е₂^/

 е^/₁

 о^/

           е₂ L

     х

о е₁ Рис. 2

 

 

 

 

 

 

 у х^/

 

 

 o^/ е^/₁

 

 

           е₂ е^/₂

 L х

            о      е₁    Рис. 3

 

y^/

 

 

 z 

 

 M

 

 

 

 

      е₃

 

O           е₂

 y          Рис. 4

е

   x

 

Обговорення виступів

Учні висловлюють свої враження від захисту творчих робіт, аналізують ці роботи, вносять доповнення, роблять поправки.

IV.Захист кросвордів

№1.

По вертикали:

1.Пара чисел для точки.

3. Ось необозначенная стрелкой.

7.Чем является d в формуле d² = (x₁ – x₂)² + (y₁ – y₂)².

9.Уравнением чего является формула ax + by + c = 0.

11.Если а = 0, в = 0, то прямая… оси Х.

13.Чем является k в уравнении k = (y₂ – y₁)/(x₂ – x₁) – угловым…

15.Если R = d, окружность и прямая…

16.x = (x₁ + x₂)/2, y = (y₁ + y₂)/2 – это координаты… отрезка.

18.Первая, вторая, третья…

19.Знаки + ; + имеет… четверть.

21. Какая четверть имеет знаки - ; -

23. Уравнение окружности x² + y² = R², если начало координат является… окружности.

26. Какое тригонометрическое тождество находится по формуле Y/R?

По горизонтали:

2. Как называют ось обозначенную стрелкой?

4.Ось Х называют ось…

5.Ось Y - …

6.Как называют координаты на плоскости?

8.Уравнением чего является формула (x – a)² + (y – b)² = R².

10. В формуле ax +  by + c = 0, a, b, c - … число.

12.Если с = 0, прямая проходит… координат.

14.Если R>d прямая… окружность в двух точках.

17.Что обозначается буквой R.

20.Какая четверть имеет знаки -;+?

22.Какая четверть имеет знаки +;-?

24.Как называется функция y = ax + b?

25.Что такое прямая, гипербола для функции?

       №2.

1.Как называется ось Х на координатной плоскости?

2.Как называется Х и Y для определенной точки на плоскости?

3.Как называются четыре части координатной плоскости?

4.Как ещё координаты Х и Y называются на плоскости?

5.Координаты середины чего мы находим по формуле: x = (x₁ + x₂)/2 ?

6.Расстояние между чем находится по формуле: d² = (x₁ – x₂)²+(y₁ – y₂)² ?

7.Если по формуле d²=(x₁ – x₂)²+(y₁ – y₂)²  d=0, то что происходит с точками на плоскости?

8.Любые 2 числа, которые удовлетворяют этому уравнению, являются координатами некоторой точки… чего?

9.Уравнение чего находится по формуле (x – a)²+(y – b)²=R² ?

10.Уравнение чего находится по формуле ax+by+c=0 ?

11.Как называется коэффициент k в уравнении прямой?

12.График какой функции задаётся формулой y=kx+c?

13.Что является графиком линейной функции?

14.С чем пересекается прямая в системе уравнений x²+y²=R², x=d?

15.Если точка лежит на оси ординат, то чему равен Х?

5. Підсумок уроку

Вчитель підсумовує учнівські виступи та доповнення до них, вказує на культуру математичного мовлення і мовлення взагалі, на лаконічність та ясність доповідей та відповідей на запитання.

6. Оцінювання

Оцінки виставляються за основні виступи та доповнення.

                                   Підготувала:

вчитель математики   Данішевська Т.Ф.

 

 

ВИСНОВКИ

 

В результаті аналізу психолого-педагогічної, методичної літератури з питань формування знань за допомогою інтерактивних технологій навчання та використовуючи дані знання на уроках ми виявили, що ці форми сприяють формуванню інтелектуальних вмінь.

У ході дослідження було розроблено його головні завдання:

1. Вивчили стан проблеми в психолого-педагогічній та методичній літературі.
2. Розкрили суть поняття інтерактивні технології навчання.
3. Застосували засоби інформаційних технологій навчання на уроках математичних дисциплін.
4. Розробили уроки на застосування різних форм організації діяльності учнів.

Данні форми викликають зацікавленість ,викликають позитивні емоції, сприяють кращому запам’ятованню матеріалу. Дитину втомлює пасивність, а праця, яка пов’язана із позитивними емоціями, сприяє гарному застосуванню та закріпленню знань.

Результати нашої роботи  показали що висунута гіпотеза підтвердилась: використання інтерактивних технології навчання, дозволили підвищити рівень знань учнів. Що доказало  свою ефективність для оволодіння уміннями навчального матеріалу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

СПИСОК ВИКОРИСТОВАНИХ ДЖЕРЕЛ

 

1. Александрова Н.В. Математические термины: Справочник. — М.: Высш. шк., 1978.
2. Бевз Г.П.Методика викладання математики: Навч.посібник –К.: Вища школа., 1989. -367с.
3. Бич О.В., Григорєва О.В. Застосування інформаційних технологій при вивченні математики. –Кривий Ріг КДПУ,2003р.
4. Борисова В.О. Міжнародний конкурс-гра „Кенгуру - 2002” // Математика – 2003 - № 7, с.18-20.
5. Борисова В.О. Міжнародний конкурс-гра „Кенгуру - 2002” // Математика – 2003 - № 8, с.7-9.
6. Вітюк О.В. Використання засобів новітніх інформаційних технологій навчання під час розв’язання стереометричних задач на обчисленого характеру. // Математика в школі. - 2000.- №5.
7. Глейзер Г.И. История математики в школе: Пособие для учителей. — М.: Просвещение, 1982.
8. Гончаренко С.У. Физика-11 параграф 49-51(65-67).
9. Карпінська І.Н. Нестандартні уроки з математики. –Тернопіль,2000.- 48с.
10. Колесников С.Я. Комп’ютерні технології навчання на уроках математики в 1-6класах . Ж. Комп ютер у школі та сім ї №1. 1998р.
11. Кл.Э.Суорц. Необыкновенная физика обыкновенных явлений.
12. Колосов А. А, Книга для внекласеного чтения по математике в старших классах. — М: Учпедгиз, 1963.
13. Кирик Л.А. Физика 11. Разноуровневые  Самостоятельные и контрольные работы по 12-бальной системе ,самостоятельные работы № 22-25
14. Майя К. Узагальнююче повторення на рівні системи понять теми „Многогранники” // Комп’ютер у школі. - 2001.- №3.
15. Підручна М.В., Янченко Г.М. Дидактичний матеріал для уроків - практикум з геометрії у 7кл., 8кл.- Тернопіль: Підручники і посібники,1998-64с.
16. Раухман А.С., Сень Я.Г.Усні вправи з геометрії 7-11кл: Посібник для вивчення. –К.: Радянська школа,1989. -160с.
17. Фридман Л.М., Турецкий Е.М.Как научиться решать задачи.: Кн. для уч-ся ст. классов  сред. шк. – М.: Просвещение,1989.-192с.
18. ЧиркоВ.О. Іннформаційна технологія і  математична освіта Комп’ютер в школі та сім’ї №2 ,1998
19. Энциклопедия «Аванта+» , физика том 2 .
20. Яиченко Г.М. Сучасні уроки з математики. – Тернопіль, 1991.-26с.