З Випускна робота Роль державної підсумкової атестації та різних типів оцінювання при викладанні математики

Полтавський обласний інститут післядипломної педагогічної освіти

ім. М.В. Остроградського

 

 

Відділ природничо-математичних дисциплін

                                                                              

 

Випускна робота

Роль державної підсумкової атестації та різних типів оцінювання при викладанні математики

Завдання для підсумкової атестації

з математики

9 клас

 

 

 

Виконала:  Стаднік Юлія Валеріївна,

учитель філії “Білицька ЗОШ І-ІІ ст. №3”

      опорного закладу “Білицька ЗОШ І-ІІІ ст. №1

      Кобеляцької районної ради

      Полтавської області”

     спеціальність математика

 

 

ПОЛТАВА

2019

 

 

ПОЯСНЮВАЛЬНА ЗАПИСКА  

Структура, зміст та оцінювання завдань атестаційної роботи

У першій частині атестаційної роботи пропонується 6 завдань з вибором однієї правильної відповіді. До кожного завдання наведено чотири можливі варіанти відповіді, з яких тільки одна є правильною.

Правильне розв’язання кожного завдання першої частини 1–6 оцінюється одним балом. Загальна сума балів за виконання завдань даної частини оцінюється 6 балами.

Друга частина атестаційної роботи складається із 4 завдань тестової форми з  вибором однієї правильної відповіді.

Правильне розв’язання кожного із завдань оцінюється двома балами. Загальна сума балів за виконання завдань даної частини оцінюється 8 балами.

Третя частина атестаційної роботи складаються із п’яти завдань відкритої форми з розгорнутою відповіддю. Такі завдання вважаються виконаними правильно, якщо учень навів розгорнутий запис розв’язування з обґрунтуванням кожного його етапу та дав правильну відповідь. Загальна сума балів за виконання завдань даної частини оцінюється 15 балами.

Четверта частина атестаційної роботи складаються із п’яти завдань відкритої форми з розгорнутою відповіддю. Такі завдання вважаються виконаними правильно, якщо учень навів розгорнутий запис розв’язування з обґрунтуванням кожного його етапу та дав правильну відповідь. Загальна сума балів за виконання завдань даної частини оцінюється 20 балами.

Переведення оцінки у балах в оцінку за 12-бальною системою оцінювання навчальних досягнень учнів

Сума нарахованих балів за виконані завдання, переводиться в оцінку за 12-бальною системою оцінювання навчальних досягнень за наступною шкалою.

 

Номери завдань	Кількість балів	Усього
1 – 6	по 1 балу	6 балів
7 – 10	по 2 бали	8 балів
11 – 15	По 3 бали	15 бали
16 – 20	по 4 балів	20 балів
Сума балів		49 бали

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Кількість набраних балів	Оцінка за 12-бальною шкалою системи оцінювання навчальних досягнень учнів
0-4	1
5 – 8	2
9 – 12	3
13 – 16	4
17 – 20	5
21 – 25	6
26 – 29	7
30 – 33	8
34 – 37	9
38 – 41	10
42 – 45	11
46 – 49	12

 

 

Завдання для підсумкової атестації

з математики

9 клас

Варіант І

Початковий рівень

1. Округліть число 22,8563 з точністю до десятих:

А) 22,8

Б) 22,86

В) 22,9

Г)22,85

2. Вкажіть, який вираз не є одночленом:

А) 4xy3

Б) 5z4

В) -4+2y

Г)

3. Обчисліть значення виразу √16+√4

А) 6

Б) 10

В) √20

Г) 2√5

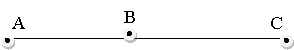4. Прямій АС належить т.В. Чому дорівнює АВ, якщо АС=10см, ВС=2см?

 

 

А) 12 см

Б) 8 см

В) 10 см

Г) 2 см

5. Вкажіть відповідні кути.

 

 

 

 

 

 

 

А)     4 та     5

Б)      6 та     7

В)      2 та      6

Г)      3 та      5

 

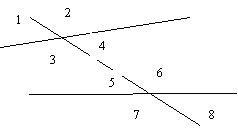
6. Обчисліть діаметр кола, якщо його радіус дорівнює 10 см.

А) 5 см

Б) 20 см

В) 10 см

Г) 25 см

 

Середній рівень

7. Вкажіть рівняння рівносильне даному: 3x – 2=5.

А) 3x = 5:2

Б) 3x =5-2

В) 3x=5+2

Г) 3x=5

8. Яка з наведених функцій не є лінійною?

А) y=x+1

Б) y=2+x

В) y=x2

Г) y=x-1

9. Менша основа трапеції дорівнює 5 см, а середня лінія – 8 см. Знайдіть більшу основу трапеції.

А) 22 см

Б) 16 см

В) 27 см

Г) 11 см

10.  В магазині светр коштує 300 грн, а в бутіку на 26% дорожче. Наскільки гривень светр дорожчий в бутіку, ніж в магазині?

А) на 75 грн

Б) на 81 грн

В) на 72 грн

Г) на 78 грн

 

Достатній рівень

11.  Спростіть вираз .
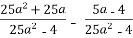12. Розв’яжіть рівняння .
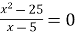13.  Знайдіть номер члена арифметичної прогресії 6, 14, 22, …, який дорівнює 214.
14.  Трикутники ABC та DEF подібні. AB =18 см, ВС=16 см, АС = 28 см, АВ:DE =4:5. Знайдіть сторони трикутника DEF.
15.  Розв’яжіть трикутник АВС, якщо ВС = 6√2 см, АС = 2 см,

С = 30֯.

Високий рівень

16.  Побудуйте графік функції y= -x²+6x-5 та знайдіть:

1). Область значень функції;

2). Область визначень функції.

17.  Човен пливе за течією річки 10 км, а потім піднімається проти течії на 6 км. Швидкість течії річки дорівнює 1 км/год. Знайти власну швидкість човна, якщо вся поїздка зайняла 4 год. У яких межах може змінюватися швидкість човна, щоб уся поїздка зайняла від трьох до чотирьох годин?
18.  Знайдіть значення виразу Знайдіть значення виразу
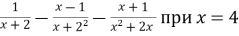
19.  Один із кутів трапеції дорівнює 30֯, а прямі, на яких лежать бічні сторони трапеції, перетинаються під прямим кутом. Знайдіть довжину меншої бічної сторони трапеції, якщо її середня лінія дорівнює 10 см, а одна з основ 8 см.
20. Знайдіть перший член і знаменник геометричної прогресії (b_n), якщо b₄ – b₁ = - 9 і b₂ +b₃+b₄= - 6.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Варіант ІІ

Початковий рівень

1. Округліть число 75,0069 з точністю до сотих:

А) 75,00

Б) 75,1

В) 75,01

Г)75,02

2. Вкажіть, який вираз не є одночленом:

А) 0,5 y

Б) 8x2

В) 2y

Г)

3. Обчисліть значення виразу √100-√25

А) 2

Б) 10

В) 5

Г) 2

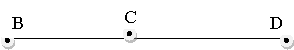4. Прямій BD належить т.C. Чому дорівнює ВC, якщо BD=12см, СD=7см?

 

 

 

А) 12 см

Б) 10 см

В) 5 см

Г) 19 см

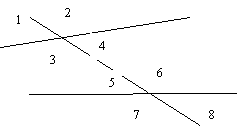
5. Вкажіть односторонні кути.

 

 

 

 

 

А)     2 та     3

Б)      6 та     7

В)      2 та      6

Г)      3 та      5

6. Обчисліть радіус кола, якщо його діаметр дорівнює 20 см.

А) 40 см

Б) 20 см

В) 50 см

Г) 10 см

 

Середній рівень

7. Серед наведених нижче рівнянь укажіть рівняння коренем якого є число -1.

А) 3x -8=11

Б) 3x-2=-5

В) 3x+1=-8

Г) 3x+8=1

8. Яка з точок належить графіку функції y=2x+7

А) (-1;5)

Б)(-1;-5)

В) (1;5)

Г) (0;5)

9. Більша основа трапеції дорівнює 11 см, а середня лінія – 8 см. Знайдіть меншу основу трапеції.

А) 5 см

Б) 10 см

В) 21 см

Г) 8 см

10. Який відсоток вмісту солі у воді, якщо 400 г води міститься 18 г солі?

А) 3%

Б) 4%

В) 3,5%

Г) 4,5%

Достатній рівень

11. Спростіть вираз :
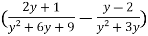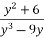
12. Розв’яжіть рівняння (3x²+7)(x²-3)-(x²-5)(x²+5)=x⁴+3x².
13. Обчисліть суму двадцяти перших членів арифметичної прогресії (a_n), якщо а₄=13, а₁₂ =61.
14. Розв’яжіть трикутник АВС, якщо ВС = 7√3 см, ВС = 1 см,

В = 150֯.

15.  Сторони паралелограма дорівнюють 8 см і 19 см, а різниця діагоналей – 10 см. Обчисліть діагоналі паралелограма.

 

Високий рівень

16. Побудуйте графік функції y= x²-2x-8 та знайдіть:

1). Проміжок зростання функції;

2). Область значень функції.

17.  Для оплати пересилки чотирьох бандеролей знадобилося чотири різних марки на загальну суму 28 грн. Знайти вартості марок, придбаних відправником, якщо вони утворюють арифметичну прогресію, а найдорожча марка у 2,5 рази дорожча від найдешевшої.
18.  Знайдіть значення виразу .
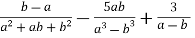19.  Перпендикуляр, опущений із вершини кута А прямокутника ABCD на діагональ, ділить її у відношенні 1:3, рахуючи від вершини В. Діагональ дорівнює 6 см. Знайдіть відстань від точки перетину до  більшої сторони прямокутника.
20.  При будь-якому n сума n перших членів деякої арифметичної прогресії S_n =3n² +5n. Знайдіть три перших члени цієї прогресії.