ЗАДАЧІ ФІЗИЧНОГО ЗМІСТУ ПРИ ВИВЧЕННІ МАТЕМАТИКИ В ЗАГАЛЬНООСВІТНІЙ ШКОЛІ
розглянути деякі питання взаємозв'язку
фізики і математики, вказати вчителеві фізики на деякі можливості,
що їх дає нова програма, підручники та навчальні посібники з
математики.
Навчально-методичне видання
Поліщук Зоя Петрівна
Федьович Микола Васильович Харченко Марія Миколаївна
ЗАДАЧІ ФІЗИЧНОГО ЗМІСТУ ПРИ ВИВЧЕННІ
МАТЕМАТИКИ
В ЗАГАЛЬНООСВІТНІЙ ШКОЛІ
Навчально-методичний посібник
Надруковано із оригінал-макета авторів
Зам.____ від ______, ______ від _________2007.
Формат 60х90/16. Ум. друк. арк.. 6,5.
Обл.. вид. арк.. 13,5. Друк різографічний. Наклад ____.
________________________________________________________
Видавництво Житомирського державного університету імені Івана Франка
ЖТ №______ від _________.
м. Житомир, вул.. Велика Бердичівська, 40 електронна пошта (E-mail) : zu@zu.edu.u Фізика і математика завжди допомагали одна одній, і розвиток їх часто нероздільний.
С. І. Вавилов
В С Т У П
Однією з умов підвищення ефективності навчального процесу та вдосконалення якості знань учнів є встановлення та реалізація міжпредметних зв’язків у процесі викладання предметів, зокрема математики та фізики.
Вивчення математики та інших природничих і технічних дисциплін відбувається паралельно, вони доповнюють одна одну. Учні повинні вивчати математику не як окремий предмет, а у взаємозв’язку з іншими предметами природничого циклу. Це дає можливість:
– значно розширити світогляд учнів;
– поглибити знання та підвищити їх якість;
– допомогти учням краще зрозуміти практичну значимість матеріалу, що вивчається;
– зацікавити учнів фізико-математичними дисциплінами.
Часто ж знання з одного предмета використовуються під час викладання іншого цілеспрямовано, з метою показати практичне застосування матеріалу й активізувати пізнавальну діяльність учнів. Мета цієї роботи — розглянути деякі питання взаємозв'язку фізики і математики, вказати вчителеві фізики на деякі можливості, що їх дає нова програма, підручники та навчальні посібники з математики.
Проблема міжпредметних зв'язків у навчально-виховному процесі сучасної школи є дуже важливою. Від успішного її розв'язання багато в чому залежить підвищення ефективності навчання і виховання учнів. У школі учень має засвоїти систему знань не тільки з даного предмета, а й пізнати зв'язки даного предмета з іншими. При цьому міжпредметні зв'язки повинні відбивати об'єктивно існуючі зв’язки між науками про природу й суспільство.
Проблему міжпредметних зв’язків слід розглядати насамперед у плані формування світогляду учнів на основі філософського узагальнення знань, що їх здобувають вони при вивченні суміжних дисциплін. Маючи це на увазі, „кожний педагог, формуючи світогляд учнів, повинен об’єднати зусилля із зусиллями інших вчителів, насамперед при введені і розвитку таких загальних фундаментальних понять науки, як матерія, час, простір, рух, розвиток тощо. Формування таких понять – це основна лінія викладання основ наук. Інша можливість – розгляд з учнями методологічних проблем науки, зокрема концепції теорії пізнання, що можна успішно здійснювати при вивченні і фізики, і хімії, і математики, і біології.
Кожна шкільна дисципліна має свою специфіку реалізації міжпредметних зв'язків. Так, курс математики озброює учнів кількісними методами та прийомами опису явищ, що вивчаються в курсах фізики, хімії, біології тощо. Завдання викладачів суміжних дисциплін полягає в тому, щоб повною мірою використати на своїх уроках весь арсенал математичних знань учнів.
Реалізація принципу міжпредметних зв'язків — один з основних резервів подальшого вдосконалення навчально-виховного процесу в школі, оскільки це сприяє систематизації знань учнів, забезпечує формування світогляду, «підвищує ефективність навчання і виховання, забезпечує наскрізне застосування й закріплення знань, умінь і навичок, що їх набули учні на уроках з різних предметів. Нарешті, реалізація міжпредметних зв'язків дає змогу підвищити ефективність (одночасно сприяє полегшенню) роботи самих школярів. Усім цим і зумовлена виняткова важливість і актуальність проблеми міжпредметних зв'язків у навчально-виховному процесі».
Застосування нової математичної символіки у фізиці в багатьох випадках дає змогу записати умову задачі і її розв'язання коротше. Привчаючи учнів правильно користуватися математичною символікою, можна досягти також певного виховного ефекту: виробити звичку до точності й лаконічності в письмовій та усній мові. Так, використання нових символів при розв'язуванні задач на побудову зображень у тонких лінзах, сферичних і плоских дзеркалах допомагає зробити пояснення символічними.
Тепер у школі вивчають основи сучасної математики
з її новими ідеями, математичним апаратом, сучасною термінологією та символікою.
Тому вчитель фізики повинен докладно ознайомитися із змістом програми з математики,
підручниками й навчальними посібниками з математики, обов'язково знати сучасну термінологію
і символіку для того, щоб використовувати міжпредметні зв'язки для формування
в учнів міцних і глибоких знань
з фізики.
I. АЛГЕБРА
1.ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ
Задачі цього типу викликають певні труднощі в учнів. Їх розв’язування слід розпочати з визначення коефіцієнта пропорційності.
Задача 1.
Відстань між Києвом і Тернополем дорівнює 360 км. Яка відстань між цими містами на карті з масштабом 1:5000000?
Розв’язання:
Оскільки масштаб карти 1:5000000, 1 см на карті відповідає 5000000 см=50 км на місцевості. Нехай відстань між Києвом і Тернополем на карті дорівнює х см. Тоді:
1 см — 50 км; х см — 360 км.
Відстань на місцевості прямо пропорційна відстані на карті.
![]()
![]() Тому 1 = 50 , звідки х = 1 см⋅360 км = 7,2 см. х 360 50
км
Тому 1 = 50 , звідки х = 1 см⋅360 км = 7,2 см. х 360 50
км
Відповідь: відстань між містами на карті 1,7 см.
Задача 2.
Відстань на карті між двома містами дорівнює 23 см. Яка відстань між цими містами на місцевості, якщо карта має масштаб
1:2000000?
Розв’язання:
Оскільки масштаб карти 1:2000000, 1 см на карті відповідає 2000000 см=20 км. Нехай відстань між цими містами на місцевості дорівнює х км:
1 см — 20 км; 23 см — х км. 1:23=20:х;
х![]() .
.
Відповідь: відстань між містами на місцевості 460 км.
Задача 3.
Відстань між двома містами на місцевості дорівнює 360 км. Яка відстань між ними на карті, що має масштаб 1:8000000?
Розв’язання:
Оскільки масштаб карти 1:8000000, 1 см на карті відповідає 8000000 см=80 км. Нехай відстань між містами на карті дорівнює х км:
1 см — 80 км; х см — 360 км.
1:х=80:360;
360 км⋅1см
х
= ![]() = 4,5 см.
= 4,5 см.
80 км
Відповідь: відстань між двома містами на карті 4,5 см.
Задача 4.
Відстань між двома пунктами на місцевості дорівнює 195 км, а на карті — 6,5 см. Знайдіть масштаб карти.
Розв’язання:
![]() 195 км=195000000см. М
=195000000см=1950000000см=30000000.
195 км=195000000см. М
=195000000см=1950000000см=30000000.
6,5см 65см
Відповідь: масштаб карти 1:30000000.
Задача 5.
Сплав складається з міді, цинку і нікелю, маси яких відносяться як 13:3:4. Знайти масу сплаву, якщо для його виготовлення використали 1,8 кг цинку. (Відношення 13:3:4 означає, що у сплаві на мідь припадає 13 частин, на цинк — 3 таких же за масою частини т на нікель — 4 частини.)
Розв’язання:
Сплав складається з 13+3+4=20 частин, з яких на цинк припадає 3 частини. Нехай маса сплаву дорівнює х кг. Тоді:
20 частин — х кг; 3 частини — 1,8 кг.
За сталої частини кількість частин та їх маса прямо пропорційні.
![]() Тому 20 = х , звідки: х
=
Тому 20 = х , звідки: х
= ![]() 20⋅1,8 кг =12 кг.
20⋅1,8 кг =12 кг.
3 1,8 3
Відповідь: маса сплаву 12 кг. Задача 6.
Сплав містить 36% заліза. Скільки кілограмів заліза міститься у
970 кг сплаву?
Розв’язання:
100 кг сплаву — 36 кг заліза
970 кг сплаву — х кг заліза
100:970=36:х;
970 кг ⋅36 кг
х
= ![]() = 349,2 кг.
= 349,2 кг.
100 кг
Відповідь: у 970 кг сплаву міститься 349,2 кг заліза.
Задача 7.
Сплав складається з міді, олова й сурми, взятих у відношенні
1:2:2. Знайдіть масу сплаву, якщо він містить 2,8 кг олова.
Розв’язання:
1.Знайдемо скільки частин становить весь сплав.
1ч+2ч+2ч=5ч
2.Знайдемо скільки припадає олова на 1 частину?
2,8 кг:2=1,4 кг.
3.Знайдемо масу всього сплаву
1,4кг ⋅5 = 7кг. Відповідь: маса сплаву 7 кг.
Задача 8.
У процесі перегонки нафти з неї отримують 30% гасу. Скільки потрібно нафти, щоб одержати 9 т гасу?
Розв’язання:
Маса нафти становить 100%, а маса гасу — 30%. Нехай щоб одержати 9 т гасу, потрібно переробити х т нафти. Запишемо умову задачі у вигляді схеми:
х т — 100%; 9 т — 30%.
![]() Складаємо пропорцію: х = 100; звідки х =
Складаємо пропорцію: х = 100; звідки х = ![]() 9 т⋅100 % = 30 т —
9 т⋅100 % = 30 т —
9 30 30 %
маса нафти.
Відповідь: маса нафти 30 т.
Задача 9.
За 8 годин токар виготовив 17 деталей. Скільки годин потрібно токареві для виготовлення 85 деталей, якщо він працюватиме з тією самою продуктивністю?
Розв’язання:
8 годин — 17 деталей;
х годин — 85 деталей.
8 17
![]() = ; х 85
= ; х 85
х ![]() .
.
Відповідь: для виготовлення 85 деталей, токареві потрібно 40
год.
Задача 10.
Певне замовлення при одночасній роботі 5 автоматів виконується за 12 год. За скільки годин буде виконано те саме замовлення при одночасній роботі 8 автоматів?
Розв’язання:
Нехай 8 автоматів виконають замовлення за х год. Оскільки із збільшенням числа автоматів у кілька разів час виконання замовлення зменшується у стільки ж разів, то час виконання замовлення обернено пропорційний до числа автоматів. За властивістю обернено пропорційних змінних відношення х до 12 дорівнює оберненому відношенню 8 до 5:
х 5
![]() = .
= .
12 8
Звідси: 8х =12⋅5,
х ![]() .
.
Відповідь: при одночасній роботі 8 автоматів, те саме замовлення буде виконано за 7,5 год. Задача 11.
Для перевезення піску планували виділити 15 самоскидів вантажністю 4 т кожний. Скільки самоскидів вантажністю 5 т слід виділити для виконання тієї самої роботи?
Розв’язання:
15 самоскидів — 4 т; х самоскидів — 5 т.
15 5
![]() = ;
= ;
х 4
х ![]() (самоскидів).
(самоскидів).
Відповідь: для виконання тієї самої роботи потрібно виділити 12 самоскидів вантажністю 5 т.
Задача 12.
Скільки важить бензин, об’єм якого 25 л?
Розв’язання:
Нам потрібно знайти вагу бензину Р
V = 25 л = 0,025 м3;
кг ρбензину =
0,7 ![]() 3 ; м
3 ; м
м
g
= 9,8 ![]() 2 .
2 .
с
. Ми знаємо, що вага тіла прямо пропорційна масі і прискоренню вільного падіння тіла за другим законом Ньютона.
P=m⋅g;
m=ρ⋅V ;
P![]() . м с с
. м с с
Відповідь: вага бензину становить 0,17 Н.
Задача 13.
Довжина меншого плеча важеля 5 см, більшого 30 см. На менше діє сила 12 Н. Яку силу треба прикласти до більшого плеча, щоб зрівноважити важіль?
Розв’язання:
Нам потрібно знайти силу, яку треба прикласти до більшого плеча F2.
l1 = 5 см = 0,05 м; l2 = 30 см = 0,3 м;
F1 =12 H.
![]() За умовою рівноваги важеля, сили
прикладені до плечей, обернено пропорційні довжинам плечей: F1 l2
За умовою рівноваги важеля, сили
прикладені до плечей, обернено пропорційні довжинам плечей: F1 l2
= ;
F2 l1
![]() F1 ⋅l1 12 H ⋅0,05 м
F1 ⋅l1 12 H ⋅0,05 м
F2 = = = 2 Н. l2 0,3 м
Відповідь: щоб зрівноважити важіль, до більшого плеча потрібно прикласти силу в 2 Н.
Задача 14.
Який тиск на підлогу чинить хлопчик, маса якого 48 кг, а площа підошв його взуття 320 см2.
Розв’язання:
Нам потрібно знайти тиск на підлогу, який чинить хлопчик Р. m = 48 кг;
S = 320 см2 = 0,032 м2;
м
g =
9,8 ![]() 2 .
2 .
с
F
P
= ![]()
S
Сила F , з якою хлопчик тисне на підлогу, дорівнює mg. Тоді
тиск на підлогу
P =
![]() mg , де тиск прямо пропорційний
масі і S
mg , де тиск прямо пропорційний
масі і S
прискоренню вільного падіння і обернено пропорційний площі підошов взуття.
м
48 кг ⋅9,8 2
![]() Р = 2с =14700
Р = 2с =14700 ![]() Н2 =14700 Па.
Н2 =14700 Па.
0,032м м
Відповідь: тиск, який хлопчик чинить на підлогу становить
14700 Па.
Задача 15.
Неоднорідний стержень АВ має довжину 12см. Маса його частини АВ зростає пропорційно квадрату відстані точки М від кінця А і дорівнює 10г при АМ=2см. Знайдіть масу всього стержня і лінійну густину в точках А і В.
Розв’язання: Нехай довжина відрізка АМ = х(см), тоді m = kx2 , де k— коефіцієнт пропорційності. Маємо
10 = k ⋅22 , k = 2,5.
Маса стержня дорівнює: m = 2,5⋅(12см)2 = 360г. Лінійна густина дорівнює: ρl = m′(x) = 2kx = 5x.
В точці А m′(x) = m′(0) = 0.
В точці В m′(x) = m′(12) = 5⋅12 = 60.
Відповідь: маса всього стержня становить 360 г, а лінійна
густина в точках А становить
0 ![]() г 3 , а в точці В становить
60
г 3 , а в точці В становить
60 ![]() г 3 . см см
.
г 3 . см см
.
2.ЗАДАЧІ НА НАЙБІЛЬШЕ І НАЙМЕНШЕ ЗНАЧЕННЯ
Проблема знаходження найменших та найбільших значень відіграє важливу роль в фізиці, техніці та економіці. Мова йде про визначення оптимально можливих значень фізичних і інших величин, економії часу, енергії, матеріалів, про попередження аварійних ситуацій і ін.
Запропоновані задачі носять вибірковий характер, вони лише в невеликій мірі відображають масштабність цієї проблеми.
Задача 1.
Електричні заряди q1 = 5нКл і q2 =11нКл розміщені на відстані r один від одного. Яким чином слід перерозподілити заряди, щоб сила взаємодії між ними була найбільшою?
Розв’язання:
За законом Кулона сила взаємодії між зарядами
![]() q1 ⋅ q2
q1 ⋅ q2
F = k ⋅ 2 .
r
Відповідь: оскільки k і r є сталими, то щоб отримати максимальну силу, треба лише перерозподілити заряди. Для отримання найбільшої сили потрібно від q2 відняти 3нКл і передати q1. Задача 2.
Електричне коло складається з двох паралельно з’єднаних провідників. При якому співвідношенні між опорами цих провідників опір найбільший, якщо при послідовному з’єднанні опір кола дорівнює 6 Ом?
Розв’язання:
При послідовному з’єднанні: R = R1 + R2 ,
![]() при паралельному— 1 = 1 + 1 , R =
при паралельному— 1 = 1 + 1 , R = ![]() R1R2 .
R1R2 .
R R1 R2 R1 + R2
Оскільки R1 + R2 = 6 = const, то R1R2 досягає найбільшого значення при R1 = R2 = 3(Ом) і, відповідно,
R1R2 9
![]() R
= = =1,5.
R
= = =1,5.
R1 + R2 6
Зауваження: при розв’язуванні двох останніх задач була використана теорема:
Добуток двох додатних множників, сума яких є сталою, має найбільше значення при рівності множників.
Покажемо ще один спосіб розв’язування останньої задачі.
![]() R1R2 R1(6 − R1 )
R1R2 R1(6 − R1 )
R = = ,
R1 + R2 6
R′(R1 ) = ![]() (6 − 2R1 ), 6 − 2R1 = 0, R1 = 3, R2 = 3,
(6 − 2R1 ), 6 − 2R1 = 0, R1 = 3, R2 = 3,
R′′(R1 ) < 0
і ми маємо максимум.
Відповідь: при співвідношенні R′′(R1 )< 0 між опорами цих провідників опір найбільший.
Задача 3.
Річка шириною 120м тече зі швидкістю
1,5 ![]() м. Човняр, який с
м. Човняр, який с
може гребти зі швидкістю
2,5 ![]() м, хоче досягти протилежного
берега в с
м, хоче досягти протилежного
берега в с
найкоротший час. Знайдіть цей час і напрям руху човняра відносно берега.
Розв’язання:
Для досягнення поставленої цілі необхідно, щоб результуюча швидкість була направлена перпендикулярно до берегів річки
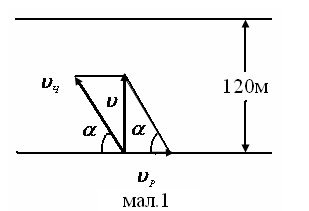 (найменшій
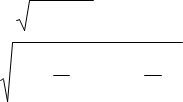
відстані відповідає найменша затрата часу) (мал.1) υ= υч2 −υр2 =
(найменшій
відстані відповідає найменша затрата часу) (мал.1) υ= υч2 −υр2 =
м2 м2 м
= 2,5 −1,5 = 2 ![]() ,
,
с с с
t![]() ),
),
2
tgα= ![]() ≈1,33,
≈1,33,
1,5 α≈ 53°.
Відповідь: час, за який човняр досягне протилежного берега, становить 60 с, напрям руху човняра відносно берега становить ≈ 53°.
Задача 4.
 Між точками А
і В рухається по прямій тіло так, що виходячи з точки А з початковою
швидкістю υ0 = 0, воно повинно мати в
точці В швидкість υ= 0. При цьому тіло може рухатися з сталим
за модулем прискоренням і рівномірно. Яким має бути характер руху, щоб час руху
був мінімальним?
Між точками А
і В рухається по прямій тіло так, що виходячи з точки А з початковою
швидкістю υ0 = 0, воно повинно мати в
точці В швидкість υ= 0. При цьому тіло може рухатися з сталим
за модулем прискоренням і рівномірно. Яким має бути характер руху, щоб час руху
був мінімальним?
Розв’язання:
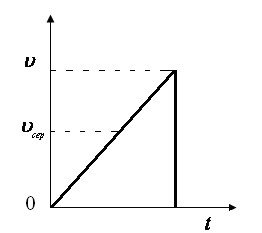
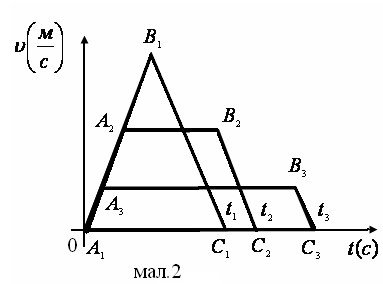
Пройдений шлях може бути зображений у вигляді площі трапеції чи трикутника (мал.2).
SABC1 1 1 = SA AB C1 2 2 = SA A B C1 3 3 3 ,
A1C1 < A1C2 < A1C
3
або t1 < t2 < t3.
Відповідь: першу половину часу тіло повинно рухатись рівноприскорено, а другу половину рівносповільнено.
В задачі ми використали деяке твердження, яке доцільно було б довести.
Твердження. Якщо рівність:
1 1 1 1
![]() =
+ +...+
=
+ +...+ ![]() , а
а1 а2 ап
, а
а1 а2 ап
де а > 0, a1 > 0, a2 > 0, ..., an > 0, то а < a1, a < a2 , ...,a < an. Доведення:
1 1 a1 − a
![]() − >
0,
− >
0, ![]() > 0, a1 > a, a < a1 і т.д. a a1 aa1
> 0, a1 > a, a < a1 і т.д. a a1 aa1
Дане твердження має велике практичне значення в фізиці, електротехніці і ін. Задача 5.
Електричне коло має деякий опір (значення цього опору може бути відомим або невідомим). Потрібно змінити опір кола так, щоб він став меншим 5 Ом.
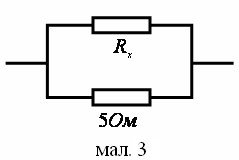 Для розв’язання цієї
задачі достатньо паралельно підключити провідник з опором R ≤ 5Ом (мал.3).
Для розв’язання цієї
задачі достатньо паралельно підключити провідник з опором R ≤ 5Ом (мал.3).
1 1 1
![]() = + , R < 5. R Rx 5
= + , R < 5. R Rx 5
Задача 6.
До конденсатора ємності Сх треба приєднати інший так, щоб в результаті отримали ємність, меншу 3мкФ.
Розв’язання:
При послідовному з’єднанні конденсаторів:
1 1 1 1
![]() = + +...+
= + +...+ ![]() .
.
С С1 С2 Сп
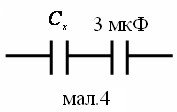 До конденсатора ємності Сх треба послідовно підключити
інший конденсатор ємністю С ≤
3мкФ.(мал.4).
До конденсатора ємності Сх треба послідовно підключити
інший конденсатор ємністю С ≤
3мкФ.(мал.4).
1 1 1
![]() = + , С < 3. С Сх 3
= + , С < 3. С Сх 3
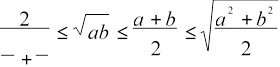 Теорема: якщо a >
0 i b >
0 , то
Теорема: якщо a >
0 i b >
0 , то
.
1 1
a b
Доведення.
![]() 2ab 2ab
− a ab − b ab −
2ab 2ab
− a ab − b ab −
− ab = = a + b a + b
(Інші нерівності доводяться аналогічно).
ab( a − b)2
≤ 0.
a + b
Задача 7. r r
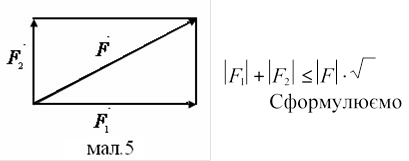 Доведіть, що коли дві сили F1 і F2 прикладені до однієї точки
під кутом 90°,
то 2 , де F - рівнодійна F1 i F2 .
Доведіть, що коли дві сили F1 і F2 прикладені до однієї точки
під кутом 90°,
то 2 , де F - рівнодійна F1 i F2 .
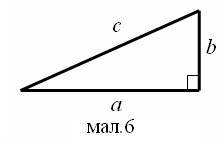
задачу по-іншому. Доведіть, що в прямокутному трикутнику найбільше значення суми довжин катетів
 дорівнює
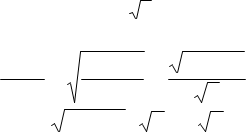
довжині гіпотенузи, помноженої на 2 (мал.5, 6). Доведення.
дорівнює
довжині гіпотенузи, помноженої на 2 (мал.5, 6). Доведення.
a + b a2 + b2 a2 + b2
≤ = ,
2 2 2 a + b ≤ a2 + b2 ⋅ 2 = c 2.
Задача 8.
Визначте мінімальну відстань між предметом і його дійсним зображенням в збиральній лінзі з фокусною відстанню F .
Розв’язання.
Перший спосіб розв’язування:
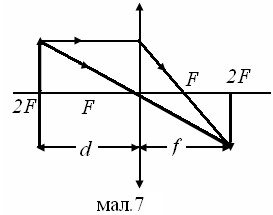 1 1 1
1 1 1
![]() + = —формула тонкої d f F
+ = —формула тонкої d f F
лінзи, де d - відстань від предмета до лінзи, f - відстань від лінзи до зображення предмета, F – фокусна
відстань.
d + f 2
 ≥ = ,
≥ = ,
1 1
+
d f
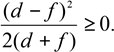
Найменшій відстані d + f відповідає d = f (мал.7).
![]() З 1 + 1 = 1 знаходимо d f F
З 1 + 1 = 1 знаходимо d f F
1 2
![]() = ,
F d
= ,
F d
d = 2F,
.
d 2
a = ![]() , d
− F d + f = 4F.
, d
− F d + f = 4F.
Другий спосіб:
Нехай d + f = a, f = a − d ,
1 1 1
![]() + = ,
+ = ,
d a − d F d 2
a
= ![]() ,
,
d − F
d 2 − ad + aF = 0,
![]() a ± a 2 −
4aF d =,
a ± a 2 −
4aF d =,
2
a 2 − 4aF ≥ 0, amin = 4F або (d + f )min = 4F.
Третій спосіб:
dF dF d 2 (d − 2F)2
![]() f =
f =
![]() , d
+ f =
, d
+ f = ![]() + d = = + 4F. d − F d − F d − F d − F
+ d = = + 4F. d − F d − F d − F d − F
При d = 2F маємо найменшу відстань, що дорівнює 4F. Четвертий спосіб:
d 2
d + f = ![]() ; d
− F
; d
− F
![]() (d +
f )′(d ) =
2d(d −
F) −2 d 2 =
d 2 − 2dF2 ;
(d +
f )′(d ) =
2d(d −
F) −2 d 2 =
d 2 − 2dF2 ;
(d − F) (d − F)
d 2 − 2dF = 0, d = 2F. При d = 2F f = 2F,a d + f = 4F.
Принцип Ферма П’єр Ферма (1601-1665 рр.) в результаті розв’язування багатьох задач проголосив так званий принцип найменшої дії. Згідно цього принципу природа змушує всі явища відбуватися з найменшою затратою енергії, часу і ін. (Принцип Ферма не є універсальним).
Наприклад, світло вибирає із всіх можливих траєкторій, що з’єднують дві точки, ту, яка вимагає найменшого часу.
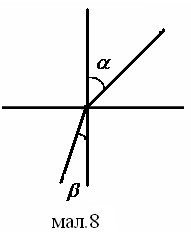 Якщо застосовувати
принцип Ферма до закону заломлення світла—час проходження границі двох середовищ
мінімальний при
Якщо застосовувати
принцип Ферма до закону заломлення світла—час проходження границі двох середовищ
мінімальний при ![]() =
=
![]() , де υ1 iυ2 —швидкості поширення
, де υ1 iυ2 —швидкості поширення
світла в різних середовищах, наприклад в повітрі і воді, α—кут падіння, β—кут заломлення. (мал.8)
Задача 9.
Пішохід повинен пройти з пункту А, що знаходиться на одному тротуарі, в пункт В, що знаходиться на другому тротуарі. Знаючи, що швидкість руху по тротуару в µ раз (µ>1) більша, ніж по бруківці, визначте, під яким кутом φ пішохід повинен перейти вулицю для того, щоб подолати шлях в найкоротший час.
Розв’язання:
υ sin(90° −α) 1 1
![]() = , = cosϕ,ϕ= arccos
= , = cosϕ,ϕ= arccos ![]() . µυ
sin90° µ
µ
. µυ
sin90° µ
µ
Якщо допустити, наприклад, що µ=2,то ϕ= 60°.
Відповідь: для того, щоб подолати шлях в найкоротший час,
пішохід повинен перейти вулицю під кутом ϕ= arccos ![]() 1 .
1 .
µ
3.РОЗВ’ЯЗУВАННЯ СЮЖЕТНИХ ЗАДАЧ МЕТОДОМ РІВНЯНЬ
Задача 1.
Катер у стоячій воді йде зі швидкістю
20 ![]() км . Швидкість течії
год
км . Швидкість течії
год
річки 2 ![]() км . Знайдіть відстань між двома пристанями,
якщо рейс год туди й назад катер здійснює за 5 год.
км . Знайдіть відстань між двома пристанями,
якщо рейс год туди й назад катер здійснює за 5 год.
Розв’язання:
Швидкість катера за течією дорівнює 20 + 2 = 22( ![]() км ); год
км ); год
швидкість катера проти течії дорівнює
20 − 2 =18( ![]() км ). год
км ). год
Нехай
x — відстань між двома пристанями. Тоді, пливучи за течією, катер витрачає
![]() x годин; а, пливучи проти
течії, витрачає
x годин; а, пливучи проти
течії, витрачає
22
x ![]() годин.
годин.
18
Отримаємо:
x x 9x +11x
![]() + = 5, звідси
+ = 5, звідси ![]() = 5, 20x = 990,x = 49,5.
= 5, 20x = 990,x = 49,5.
22 18 198
Відповідь: відстань між пристанями 49,5 км.
Задача 2.
Катер у стоячій
воді проходить 15 ![]() км ,швидкість течії річки год
км ,швидкість течії річки год
км
2 ![]() . Знайдіть
відстань між двома пристанями, якщо в один бік год
. Знайдіть
відстань між двома пристанями, якщо в один бік год
катер проходить її на півгодини швидше, ніж у другий. Розв’язання:
![]() Нехай відстань між двома пристанями
х км. Швидкість катера за течією дорівнює: 15 км + 2 км =17
Нехай відстань між двома пристанями
х км. Швидкість катера за течією дорівнює: 15 км + 2 км =17 ![]() км , швидкість катера
проти год год год
км , швидкість катера
проти год год год
![]() течії — 15 км − 2 км =13
течії — 15 км − 2 км =13 ![]() км . Пливучи за течією,
катер витрачає
км . Пливучи за течією,
катер витрачає
год год год
x x
![]() годин.
Пливучи проти течії, катер витрачає
годин.
Пливучи проти течії, катер витрачає ![]() годин. Тоді
годин. Тоді
17 13
![]() отримаємо: x = x − 1 , звідси
отримаємо: x = x − 1 , звідси
17 13 2
x x 1
![]() − = − ,
− = − ,
17 13 2
![]() ,
,
![]() ,6.
,6.
Відповідь: відстань між пристанями дорівнює 27,6км. Задача 3.
Відстань ніж двома станціями потяг може проїхати зі швидкістю
70 ![]() км на півгодини швидше, ніж зі швидкістю
60
км на півгодини швидше, ніж зі швидкістю
60 ![]() км . Знайдіть цю год год
км . Знайдіть цю год год
відстань.
Розв’язання:
Нехай хкм – відстань між двома станціями, тоді зі швидкістю
70 ![]() км , потяг проходить
цю відстань за
км , потяг проходить
цю відстань за ![]() x годин; а зі год 70
x годин; а зі год 70
![]() швидкістю
60
швидкістю
60 ![]() км – за
км – за ![]() x годин. Отримаємо: x + 1 = x , звідси год
60 70 2 60
x годин. Отримаємо: x + 1 = x , звідси год
60 70 2 60
6x + 210 7x
![]() = , 420 420
= , 420 420
6x + 210 = 7x,
x = 210.
Відповідь: відстань між двома станціями рівна 210 км.
Задача 4.
Пасажирський потяг протягом 3 год проходить на 10 км більше,
ніж товарний протягом 4 год. Швидкість товарного потяга
на 20 ![]() км год
км год
менша від швидкості пасажирського. Знайдіть ці швидкості.
Розв’язання:
Нехай швидкість пасажирського потяга дорівнює х ![]() км
, год
км
, год
тоді швидкість
товарного потяга — (x −
20)
![]() км . год
км . год
Протягом 3 годин пасажирський потяг пройде 3x км.
Протягом 4 годин товарний потяг пройде 4(x − 20) км.
Складемо рівняння, виходячи з умов задачі:
3x − 4(x − 20) =10. Розв'яжемо це рівняння:
3x − 4(x − 20) =10,
3x − 4x +80 =10,
− x = −70, x = 70.
Швидкість пасажирського потяга дорівнює 70 ![]() км , тоді год
км , тоді год
швидкість товарного потяга дорівнює 70 ![]() км − 20
км − 20 ![]() км = 50
км = 50 ![]() км .
км .
год год год
Відповідь: швидкість пасажирського потяга дорівнює 70 ![]() км ,
км ,
год
швидкість товарного потяга дорівнює 50 ![]() км . год Задача
5.
км . год Задача
5.
Велосипедист їхав 2 год ґрунтовою дорогою і 1 год асфальтованою — всього 28 км. Знайдіть його швидкість на кожній ділянці дороги, якщо асфальтованою дорогою він їхав зі швидкістю
на 4 ![]() км більшою, ніж ґрунтовою.
км більшою, ніж ґрунтовою.
год
Розв’язання:
Нехай х ![]() км — швидкість велосипедиста
на асфальтованій год
км — швидкість велосипедиста
на асфальтованій год
дорозі; тоді (x
− 4)
![]() км — швидкість велосипедиста
на ґрунтовій год
км — швидкість велосипедиста
на ґрунтовій год
дорозі.
Складемо рівняння, виходячи з умов задачі: x + 2(x − 4) = 28. Розв'яжемо це рівняння:
x + 2(x − 4) = 28;
x + 2x −8 = 28,
3x = 36, x =12.
Відповідь: по асфальтованій дорозі велосипедист їхав зі
швидкістю 12 ![]() км , по ґрунтовій — 8
км , по ґрунтовій — 8
![]() км . год год
км . год год
Задача 6.
Від станції до турбази туристи йшли зі швидкістю 4 ![]() км , а нагод
км , а нагод
зад — зі швидкістю
5 ![]() км , і тому на той самий
шлях витратили на год
км , і тому на той самий
шлях витратили на год
годину менше. Знайдіть відстань від станції до турбази.
Розв’язання:
Нехай відстань від станції до турбази x км. Тоді, ідучи
зі швидкістю 4 ![]() км , туристи витратили
км , туристи витратили
![]() x годин, ідучи зі швидкістю
год 4
x годин, ідучи зі швидкістю
год 4
км x
![]() 5 - годин.
год 5
5 - годин.
год 5
Отримаємо: ![]() x −1
=
x −1
= ![]() x,
x,
4 5
звідси
5x − 20 4x
![]() = ,
= ,
20 20
5x − 20 = 4x, x = 20.
Відповідь: відстань від станції до турбази 20 км.
Задача 7.
Відстань між пунктами А і В по залізниці дорівнює 66 км, а по річці 80,5 км. З пункту А поїзд виходить на 4 год пізніше пароплава і прибуває до В на 15 хв раніше. Визначити середню швидкість поїзда,
якщо вона
на 30 ![]() км більша за швидкість
пароплава. год
км більша за швидкість
пароплава. год
Розв’язання:
Нехай швидкість поїзда дорівнює х ![]() км , тоді швидкість год
км , тоді швидкість год
пароплава буде (х −30)
![]() км . Весь шлях поїзд
проходить за
км . Весь шлях поїзд
проходить за ![]() 66 год, а год х
66 год, а год х
пароплав за ![]() 80,5 год. Оскільки
поїзд виходить на 4 години пізніше, а х −30
80,5 год. Оскільки
поїзд виходить на 4 години пізніше, а х −30
прибуває на 15 хвилин раніше, ніж пароплав, то поїзд був у дорозі на
4![]() год менше пароплава, тобто:
год менше пароплава, тобто:
80,5 66 1
![]() − = 4 , х −30 х 4
− = 4 , х −30 х 4
або
17х2 −568х −7920 = 0,
Звідки х1 =
−10![]() , а х2 =
44.
, а х2 =
44.
Перший корінь умову задачі не задовольняє. Отже, х=44.
Відповідь:
середня швидкість поїзда становить 44 ![]() км . год Задача
8.
км . год Задача
8.
Теплохід пройшов відстань між пристанями в
одному напрямі за 4 год, а в протилежному — за 5 год. Знайдіть відстань
ніж пристанями, якщо швидкість течії річки дорівнює 2 ![]() км . год Розв’язання:
км . год Розв’язання:
Нехай швидкість теплохода в стоячій воді дорівнює х ![]() км , год
км , год
тоді швидкість за течією дорівнює (x + 2)
![]() км , а швидкість проти
км , а швидкість проти
год
течії дорівнює (x − 2)
![]() км . Відстань між пристанями
— 4(x
+ 2)
або год 5(x −
2).
км . Відстань між пристанями
— 4(x
+ 2)
або год 5(x −
2).
Отримаємо: 4(x + 2) = 5(x − 2), звідси:
4x +8 = 5x −10, 5x − 4x = 8+10, x =18.
Швидкість теплохода в стоячій воді — 18
![]() км , тоді відстань год
км , тоді відстань год
між пристанями дорівнює: 4⋅(18+ 2) = 4⋅20 = 80(км).
Відповідь: відстань між пристанями дорівнює 80 км. Задача 9.
Вертоліт пролетів відстань між двома містами при попутному вітрі за 5,5 год, а при зустрічному — за 6 год. Знайдіть відстань між містами і власну швидкість вертольота, якщо швидкість вітру
дорівнювала 10 ![]() км . год
км . год
Розв’язання:
Нехай власна швидкість вертольота —x ![]() км , тоді швидкість год
км , тоді швидкість год
при попутному вітрі дорівнює (x
+10)
![]() км , а швидкість проти
вітру год
км , а швидкість проти
вітру год
дорівнює (x
−10)
![]() км . год
км . год
Відстань між містами дорівнює: 5,5(x +10) км або 6(x −10) км. Отримаємо: 5,5(x +10) = 6(x −10).
Звідси:
5,5x + 55 = 6x − 60;
0,5x =115, x = 230.
Швидкість вертольота дорівнює 230 ![]() км , тоді відстань між
год
км , тоді відстань між
год
містами дорівнює: 6⋅(230 −10) =1320(км).
Відповідь: відстань між містами становить
1320 км; власна швидкість вертольота становить230 ![]() км . год
км . год
Задача 10.
Швидкість моторного
човна за течією 23 ![]() км , а проти течії
км , а проти течії
год
км
17 ![]() . Знайдіть власну швидкість човна і швидкість
течії.
. Знайдіть власну швидкість човна і швидкість
течії.
год
Розв’язання:
Нехай х ![]() км – власна швидкість
моторного човна, а у
км – власна швидкість
моторного човна, а у ![]() км – год год
км – год год
швидкість течії річки, тоді х + у = 23 і х − у =17. Отримали систему рівнянь:
x + y = 23,
x − y =17;
![]()
2x = 40,x = 20 y = 23− 20, y = 3.
Відповідь: власна швидкість моторного човна дорівнює
20 ![]() км , год
км , год
швидкість течії
річки – 3 ![]() км . год
км . год
Задача 11.
Туристи проїхали 640 км, з них 7 год потягом і 4 год автобусом.
Знайдіть швидкість
потяга, якщо вона на 5 ![]() км більша від швидкості год
км більша від швидкості год
автобуса.
Розв’язання:
Нехай швидкість автобуса х ![]() км , а швидкість потяга
— у
км , а швидкість потяга
— у ![]() км .
км .
год год
Відомо, що х + 5 = у. Потягом туристи проїхали 7у км, автобусом —
4х км, всього вони проїхали 640 км, отже, 4х + 7у = 640. Розв'яжемо систему рівнянь:
х + 5 = у,
4х + 7у = 640;
4х + 7(х + 5) = 640,
4х + 7х + 35 = 640,
11х = 605, х = 55, у = 55 + 5, у = 60.
Відповідь:
швидкість потяга дорівнює 60 ![]() км . год Задача 12.
км . год Задача 12.
Два туристи вийшли одночасно з двох міст, відстань між якими
38км, і зустрілись через 4 год. З якою швидкістю йшов кожний, якщо перший до зустрічі пройшов на 2 км більше, ніж другий? Розв’язання:
Нехай швидкість
одного туриста x ![]() км , а другого — у
км , а другого — у ![]() км . За год год
км . За год год
чотири години вони пройшли відповідно 4х км і 4у км кожний. Разом вони пройшли 4х + 4у = 38(км). Оскільки перший турист пройшов на 2 км більше, ніж другий, можемо записати:
4х − 4у = 2(км).
Отримали систему рівнянь:
4х + 4у = 38,
4х − 4у = 2;
![]()
8х = 40,х = 5,
20 − 4у = 2,−4у = −18, у = 4,5.
Відповідь: швидкість першого туриста
5 ![]() км , швидкість другого
год
км , швидкість другого
год
туриста –4,5
![]() км . год
км . год
Задача 13.
Відстань 160 км легковий автомобіль проходить на 2 години швидше, ніж автобус. Знайдіть їх швидкості, якщо вони відносяться, як 2:1.
Нехай легковий автомобіль проходить 160 км за x годин, тоді автобус проходить цю відстань за (x + 2) годин. Отже, швидкість
автомобіля дорівнює 160![]() км , а автобуса
км , а автобуса
![]() 160 км
.
160 км
.
х год x + 2 год
Отримаємо рівняння:
160 160
![]() : = 2 :1. х х + 2
: = 2 :1. х х + 2
160 160
![]() : = 2; х х + 2
: = 2; х х + 2
160(х + 2)
![]() = 2;
= 2;
х⋅160 х + 2
![]() = 2; х
= 2; х
х + 2 − 2х = 0;
− х + 2 = 0;х = 2.
Дане значення х є коренем рівняння, оскільки знаменник при цьому не дорівнює 0.
Автомобіль проходить 160 км за 2 години, тоді автобус за 4
години. Отже, швидкість автомобіля дорівнює 160: 2 = 80 ![]() км , а год
км , а год
швидкість автобуса дорівнює 160: 4 = 40
![]() км .
км .
год
Відповідь: швидкість автомобіля становить 80 ![]() км ; швидкість год
км ; швидкість год
автобуса становить
40 ![]() км . год
км . год
Задача 14.
Теплохід пройшов за течією річки 48 км і стільки ж проти течії і затратив на весь шлях 5 год. Знайдіть власну швидкість теплохода,
якщо швидкість течії річки 4 ![]() км .
км .
год
власна швидкість теплохода дорівнює x ![]() км , тоді год
км , тоді год
швидкість за течією дорівнює (х
+ 4)
![]() км . На шлях за течією
теплохід год
км . На шлях за течією
теплохід год
затратив ![]() 48 годин, на шлях проти течії
–
48 годин, на шлях проти течії
– ![]() 48 годин, а всього х + 4 х − 4
48 годин, а всього х + 4 х − 4
затратив 5 годин. Отримуємо рівняння:
48 48
![]() + =
5; х + 4 х
− 4 х ≠ 4, х ≠ −4.
+ =
5; х + 4 х
− 4 х ≠ 4, х ≠ −4.
48(х − 4)+ 48(х + 4)−5(х2 −16)
![]() 2 = 0; х −16
2 = 0; х −16
−5х2 + 96х +80 = 0;
5х2 −96х −80 = 0; D = 2304 + 400 = 2704;
х![]() ;
;
х![]() ;
;
![]()
х
Очевидно, що від’ємне значення кореня не задовольняє умову
задачі. Отже, власна швидкість теплохода дорівнює 20 ![]() км . год
км . год
Відповідь: власна швидкість теплохода становить 20
![]() км . год
км . год
Задача 15.
Човен пройшов проти течії 22,5 км і за течією 28,5 км, затративши на весь шлях 8 годин. Швидкість течії річки км
2,5 ![]() .Знайдіть власну швидкість човна.
.Знайдіть власну швидкість човна.
год
власна швидкість човна дорівнює x ![]() км . Тоді швидкість год
км . Тоді швидкість год
за течією складає (х
+ 2,5)
![]() км , а швидкість проти
течії дорівнює год
км , а швидкість проти
течії дорівнює год
(х − 2,5)
![]() км . На дорогу проти
течії човен затратив
км . На дорогу проти
течії човен затратив ![]() 22,5 годин, а на год х − 2,5
22,5 годин, а на год х − 2,5
дорогу за течією
– ![]() 28,5 годин. Всього він витратив
8 годин на весь х +
2,5
28,5 годин. Всього він витратив
8 годин на весь х +
2,5
шлях. Отримуємо рівняння:
28,5 22,5
![]() + = 8;
+ = 8;
х + 2,5 х − 2,5
28,5(х − 2,5)+ 22,5(х + 2,5)−8(х 2 − 6,25)= 0;
28,5х − 71,25+ 22,5х + 56,25−8х 2 + 50 = 0;
−8х 2 + 51х + 35 = 0;
8х2 −51х −35 = 0. D = 2601+1120 = 3721;
![]() х1,2 =
х1,2 = 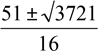 ;
;
51+ 61
х1
= ![]() = 7;
= 7;
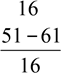 10 5
10 5
![]() х2 == − = − .
х2 == − = − .
16 8
Очевидно, що від’ємне значення кореня не задовольняє умову
задачі. Отже, власна швидкість човна
дорівнює 7 ![]() км . год
км . год
Відповідь:
власна швидкість човна становить 7 ![]() км . год
км . год
Задача 16.
Електропотяг затримався в дорозі на 4 хв і ліквідував запізнення
на перегоні в
20 км, пройшовши зі швидкістю на 10 ![]() км більшою, ніж год
км більшою, ніж год
за розкладом. З якою швидкістю йшов потяг на цьому перегоні?
швидкість електропотяга за розкладом дорівнює x ![]() км , год
км , год
тоді перегін в 20 км він проїхав
би за ![]() 20 годин, але він їхав на
цьому х
20 годин, але він їхав на
цьому х
перегоні зі швидкістю (х
+10)
![]() км і проїхав його на
4 хвилини год
км і проїхав його на
4 хвилини год
швидше. Оскільки 4 хвилини складають ![]() години, маємо рівняння:
години, маємо рівняння:
20 20 1
![]() − = ; х х
+10 15
− = ; х х
+10 15
20 20 1
![]() − − = 0; х х +10 15
− − = 0; х х +10 15
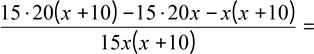 0;
0;
300х + 3000 −300х − х2 −10х = 0;
− х2 −10х + 3000 = 0; х2 +10х −3000 = 0; х = −60 або х = 50.
Від’ємне значення кореня не задовольняє умову
задачі, тому швидкість електропотяга за розкладом дорівнює 50 ![]() км , а швидкість год
км , а швидкість год
на перегоні дорівнює 60 ![]() км . год
км . год
Відповідь: потяг на перегоні їхав з швидкістю 60
![]() км . год
км . год
Задача 17.
З пункту А відправили за течією річки пліт. Через 5 год 20 хв з пункту А слідом за плотом вийшов моторний човен, який наздогнав пліт, пройшовши 20 км. Знайдіть швидкість течії річки, знаючи, що човен проходив щогодини на 12 км більше, ніж пліт.
Позначимо швидкість течії ріки через x ![]() км . Очевидно, що пліт
год
км . Очевидно, що пліт
год
рухався зі швидкістю
x ![]() км . Оскільки моторний
човен проходив за год
км . Оскільки моторний
човен проходив за год
годину на 12 км більше, можна сказати, що його швидкість була
(х
+12)
![]() км . Тоді 20 км
він пройшов за
км . Тоді 20 км
він пройшов за ![]() 20 годин. Пліт знаходився год х +12
20 годин. Пліт знаходився год х +12
в дорозі на 5 год 20 хв довше і проплив ті ж 20 км, тобто
20 20 1 1
![]() −
= 5 (тут ми врахували, що 20 хв складають
−
= 5 (тут ми врахували, що 20 хв складають ![]() години). x
x +12 3 3
години). x
x +12 3 3
Розв’яжемо це рівняння:
20 20 16
![]() − = ; х х
+12 3
− = ; х х
+12 3
20 20 16
![]() − − = 0; х х +12 3
− − = 0; х х +12 3
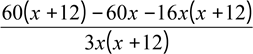 =
0;
=
0;
60х + 720 − 60х −16х2 −192 = 0; −16х2 −192х + 720 = 0; х2 +12х − 45 = 0, х = −15 або х = 3.
Від’ємне значення кореня не задовольняє умову задачі. Отже,
швидкість течії ріки дорівнює 3
![]() км . год
км . год
Відповідь:
швидкість течії річки становить 3 ![]() км . год
км . год
Задача 18.
На середині шляху між
А і В потяг затримали на 10 хв. Щоб прибути в В за розкладом,
довелось початкову швидкість потяга збільшити на 12 ![]() км . Знайдіть початкову
швидкість потяга, якщо год
км . Знайдіть початкову
швидкість потяга, якщо год
відстань між А і В дорівнює 120 км.
Позначимо початкову швидкість потяга через x ![]() км . Оскільки год
км . Оскільки год
відстань від А до В дорівнює 120 км, половина
цієї відстані дорівнює 60 км. Якщо б потяг ішов з початковою швидкістю, то
він пройшов би цю відстань за ![]() 60 годин. Він же пройшов цю відстань зі x
60 годин. Він же пройшов цю відстань зі x
швидкістю (x
+12)
![]() км і пройшов її на
10 хв або на
км і пройшов її на
10 хв або на ![]() 1 години год 6
1 години год 6
швидше. Отримуємо рівняння:
60 60 1
![]() − = ; х х +12 6
− = ; х х +12 6
60 60 1
![]() − − = 0; х х +12 6
− − = 0; х х +12 6
360(х +12)−360х − х(х +12)
= 0;
![]() 6(х
+12)х
6(х
+12)х
360х + 4320 −360х − х2 −12х = 0; − х2 −12х + 4320 = 0; х2 +12х − 4320 = 0, х = −72 або х = 60.
Від’ємне значення кореня не задовольняє умову задачі.
Початкова швидкість потяга60
![]() км . год
км . год
Відповідь: початкова швидкість потягу становить 60
![]() км . год
км . год
Задача 19.
Теплохід пройшов униз річкою 150 км і повернувся назад, витративши на весь шлях 5,5 год. Знайдіть швидкість течії річки,
якщо швидкість теплохода в стоячій воді 55 ![]() км . год Розв’язання:
км . год Розв’язання:
Позначимо швидкість течії річки через
х ![]() км . Тоді теплохід за
год
км . Тоді теплохід за
год
течією йшов зі швидкістю (55+ х)
![]() км , а проти течії зі
швидкістю
км , а проти течії зі
швидкістю
год
(55− х)
![]() км . Йдучи за течією
він затратив
км . Йдучи за течією
він затратив ![]() 150 годин, проти течії –
год 55+ х
150 годин, проти течії –
год 55+ х
150
![]() годин,
а всього затратив 5,5 годин. Складемо рівняння:
годин,
а всього затратив 5,5 годин. Складемо рівняння:
55− х
150 150
![]() + = 5,5;
+ = 5,5;
55 + х 55 − х
150 150
![]() + − 5,5 = 0;
+ − 5,5 = 0;
55 + х 55 − х
150(55 − х) + 150(55 + х) − 5,5(3025 − х 2 )
![]() =
0;
=
0;
3025 − х 2
8250 − 150х + 8250 − 150х − 16637,5 + 5,5х 2 = 0;
5,5х 2 − 137,5 = 0;
5,5х2 =137,5;
|
х2 = 25; х = ±5. |
|
|
|
|
Від’ємне значення кореня не Швидкість течії річки дорівнює 5 |
задовольняє |
умову |
задачі. |
Відповідь:
швидкість течії річки становить 5 ![]() км . год
км . год
Задача 20.
Турист проплив моторним човном вгору річкою 25 км, а назад спустився плотом. Човном він плив на 10 год менше, ніж плотом. Знайдіть швидкість течії річки, якщо швидкість човна в стоячій
воді 12 ![]() км .
км .
год
Розв’язання:
Нехай швидкість течії річки дорівнює
x ![]() км . Угору по річці год
км . Угору по річці год
моторний човен плив зі швидкістю (12− х)
![]() км , пліт плив зі год
км , пліт плив зі год
швидкістю, що дорівнює швидкості течії річки, тобто x ![]() км . На
км . На
год
моторному човні турист подолав 25 км за ![]() 25 годин, пливучи
25 годин, пливучи
12 − x
плотом, він подолав ту ж відстань за час, що на 10 годин більше часу плавання човном. Отримуємо рівняння:
25 25
![]() − =10;
x 12− x
25 25
− =10;
x 12− x
25 25
![]() − −10 = 0; x 12− x
− −10 = 0; x 12− x
25(12− x)− 25x −10(12− x)x
= 0;
![]() x(12− x)
x(12− x)
300− 25x − 25x −120x +10x2 = 0; 10x2 −170x +300 = 0; x2 −17x +30 = 0;
D = 289−120 =169;
![]() 17
± 169
17
± 169
x1.2 =;
2
x1
= ![]() =15;x2 =
=15;x2 = ![]() = 2.
= 2.
Корінь x1 =15 нам не підходить, тому що швидкість течії річки не може бути більшою швидкості моторного човна. Отже, швидкість
течії річки дорівнює 2 ![]() км . год
км . год
Відповідь:
швидкість течії річки становить 2 ![]() км . год
км . год
Задача 21.
Велосипедист проїхав 96 км на 1,6 години швидше, ніж передбачав. При цьому за кожну годину він проїжджав на 2 км більше, ніж розраховував проїжджати. З якою швидкістю він їхав? Розв’язання:
Позначимо швидкість велосипедиста через x ![]() км , тоді год
км , тоді год
швидкість, з якою передбачав їхати велосипедист, дорівнює
(х − 2)
![]() км . Відстань год
км . Відстань год
96 км він
проїхав за ![]() 96 годин і це швидше, ніж
передбачалось, х
96 годин і це швидше, ніж
передбачалось, х
на 1,6 години, тобто:
96 96
![]() − =1,6;
− =1,6;
х − 2 х
96 96
![]() −
−1,6 = 0; х
− 2 х
−
−1,6 = 0; х
− 2 х
96х −96(х − 2)−1,6(х − 2)
= 0;
![]() х(х
− 2)
х(х
− 2)
96х −96х +192 −1,6х2 + 3,2х = 0; −1,6х2 + 3,2х +192 = 0; х2 − 2х −120 = 0; х = −10 або х =12.
Від'ємне значення кореня не задовольняє умову задачі.
Швидкість велосипедиста дорівнює
12 ![]() км . год
км . год
Відповідь:
велосипедист їхав з швидкістю 12 ![]() км . год
км . год
Задача 22.
З А до В, відстань між якими 350 км, вийшов автобус. Якби він
зменшив швидкість
на 5 ![]() км , то в дорозі був
би на 1
км , то в дорозі був
би на 1![]() 2 год довше. год 3
2 год довше. год 3
Скільки годин їде автобус від А до В?
Розв’язання:
Нехай швидкість автобуса дорівнює x ![]() км , тоді відстань від
А до год
км , тоді відстань від
А до год
В він проїжджає за ![]() 350 годин. Якщо він зменшить
швидкість на 5 км, х
350 годин. Якщо він зменшить
швидкість на 5 км, х
то його швидкість буде (х
−5)
![]() км .Тоді відстань від
А до В він пройде год
км .Тоді відстань від
А до В він пройде год
за ![]() 350 годин, і це буде на
1
350 годин, і це буде на
1![]() 2 години довше. х −5 3
2 години довше. х −5 3
Складемо рівняння:
350 350 2
![]() −
=1 ; х −5
х 3
−
=1 ; х −5
х 3
350 350 5
![]() − − = 0; х −5 х 3
− − = 0; х −5 х 3
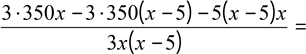 0;
0;
1050х −1050х + 5250 −5х2 + 25х = 0;
−5х2 + 25х + 5250 = 0; х2 −5х −1050 = 0; х = −30 або х = 35.
Оскільки від'ємне значення кореня не задовольняє умову задачі,
то швидкість автобуса дорівнює 35 ![]() км , тоді відстань від
А до В він год
км , тоді відстань від
А до В він год
пройде за ![]() =10
(годин).
=10
(годин).
Відповідь: автобус від А до В їде 10 годин.
Задача 23.
Мотоцикліст їхав з одного міста в друге 4 год. Повертаючись назад, він перші 100 км їхав з тією самою швидкістю, а потім
зменшив її на 10
![]() км і тому на зворотний
шлях витратив на 30 хв год
км і тому на зворотний
шлях витратив на 30 хв год
більше. Знайдіть відстань між містами.
Розв’язання:
Нехай відстань між містами дорівнює x км. Тоді початкова
швидкість мотоцикліста дорівнює ![]() x км . Перші 100 км
він проїхав за
x км . Перші 100 км
він проїхав за
4 год
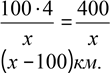 годин. Після цього йому залишилось проїхати
годин. Після цього йому залишилось проїхати
Швидкість його при цьому була
![]() x −10
x −10 ![]() км або
км або ![]() х −
40 км ,
х −
40 км ,
4 год 4 год
отже, решту шляху він подолав за (х −100):
![]() х −
40 = 4(х −100) годин.
х −
40 = 4(х −100) годин.
4 х − 40
Оскільки на зворотний шлях він витратив на 30 хвилин більше, можемо твердити, що він здолав зворотний шлях за 4,5 години.
(30 хвилин = 0,5 години). Складемо рівняння:
400 4(х −100)
![]() + = 4,5; х х − 40
+ = 4,5; х х − 40
400 4(х −100)
![]() + − 4,5 =
0; х х − 40
+ − 4,5 =
0; х х − 40
![]() 400(х
− 40)+ х(4х
− 400)− 4,5(х
− 40)
400(х
− 40)+ х(4х
− 400)− 4,5(х
− 40)
= 0;
х(х − 40)
− 0,5х2 +180х −16000 = 0; х2 −360х + 32000 = 0, х = 200 або х =160.
Обидва корені не задовольняють умову задачі. Отже, відстань між містами дорівнює або 160 км, або 200 км.
Відповідь: відстань між містами становить 160 км або 200 км.
Задача 24.
Рибалка вирушив на човні з пункту А проти течії річки. Пропливши 6 км, він кинув весла, і через 4,5 год після виходу з А течія знову віднесла його до пункту А. Знайдіть швидкість течії річки,
якщо швидкість
човна в стоячій воді 90 ![]() м . хв
м . хв
Розв’язання:
Нехай швидкість течії ріки дорівнює х ![]() км , тоді відстань 6
км
км , тоді відстань 6
км
год
рибалка проплив до пункту А без
весел за ![]() 6 годин. Швидкість човна
х
6 годин. Швидкість човна
х
проти течії (враховуючи,
що 90 ![]() м = 5,4
м = 5,4 ![]() км ) дорівнює (5,4
− х)
км ) дорівнює (5,4
− х)
![]() км . хв год год
км . хв год год
Отже, відстань 6 км від пункту А проти течії рибалка проплив за
6 ![]() годин. Всього пройшло
4,5 години після його виходу з пункту 5,4−
х
годин. Всього пройшло
4,5 години після його виходу з пункту 5,4−
х
А. Тоді:
6 6
![]() + = 4,5;
+ = 4,5;
5,4− х х
6 6
![]() + − 4,5 = 0;
+ − 4,5 = 0;
5,4− х х
6х + 6(5,4− х) − 4,5х(5,4− х)
![]() =
0;
=
0;
х(5,4 − х)
6х +32,4−6х − 24,3х + 4,5х2 = 0;
4,5х2 − 24,3х +32,4 = 0; D = 590,49 −583,2 = 7,29;
х1,2 =
![]() ;
;
х1
= ![]() = 3;х2 =
= 3;х2 = ![]() = 2,4.
= 2,4.
Обидва корені задовольняють умову задачі. Отже, швидкість
течії ріки могла бути або 3 ![]() км ,або 2,4
км ,або 2,4 ![]() км . Якщо швидкість ріки
год год
км . Якщо швидкість ріки
год год
дорівнювала 3 ![]() км , то рибалка плив
проти течії
км , то рибалка плив
проти течії ![]() 6 = 2,5 години, а за год 2,4
6 = 2,5 години, а за год 2,4
течією його знесло за ![]() = 2 години, всього 4,5 годин. Якщо швидкість
= 2 години, всього 4,5 годин. Якщо швидкість
течії ріки дорівнювала 2,4 ![]() км , то рибалка плив
проти течії год
км , то рибалка плив
проти течії год
![]() =
2години, а за течією його знесло за
=
2години, а за течією його знесло за ![]() = 2,5 години,
= 2,5 години,
всього 4,5 годин.
Відповідь: швидкість течії річки або 3
![]() км , або 2,4
км , або 2,4 ![]() км .
км .
год год
Задача 25.
Відстань між пристанями А і В теплохід проходить за течією за 5 год, а проти течії за 6 год. За скільки годин пропливе цю відстань за течією пліт?
Розв’язання:
Нехай власна швидкість теплохода дорівнює
x ![]() км ,а швидкість год
км ,а швидкість год
течії ріки — у ![]() км ;тоді за течією швидкість
теплохода становить год
км ;тоді за течією швидкість
теплохода становить год
(х
+ у)
![]() км , а проти течії
— (х
− у)
км , а проти течії
— (х
− у)
![]() км . Знайдемо, на скільки
швидше год год
км . Знайдемо, на скільки
швидше год год
теплохід пройде за течією, ніж проти течії, тобто знайдемо різницю його швидкостей: (х + у) −(х − у) = х + у − х + у = 2у.
Як бачимо, різниця швидкостей теплохода за течією і проти течії дорівнює подвоєній швидкості течії ріки. Використаємо це при розв'язуванні задачі. Позначимо відстань між пристанями А і В через
S,тоді швидкість теплохода за течією дорівнює ![]() S км , а проти течії
S км , а проти течії
5 год
становитиме ![]() S км . Пліт пливе зі швидкістю, що дорівнює швидкості
S км . Пліт пливе зі швидкістю, що дорівнює швидкості
6 год
течії ріки. Нехай він подолає цю відстань за tгодин, тоді його
швидкість (а отже, і швидкість течії ріки) дорівнює ![]() S . Як було t
S . Як було t
показано вище, різниця швидкостей теплохода за течією і проти течії дорівнює подвоєній швидкості течії ріки. Отже, можемо записати:
S S 2S
![]() − = ;
− = ;
5 6 t
1 1 2
![]() − = ;
− = ;
5 6 t 1 1 2
![]() − − = 0;
− − = 0;
5 6 t
6t −5t −60
![]() =
0;
=
0;
30t
6t −5t −60 = 0; t −60 = 0;t = 60.
Пліт подолає цю відстань за 60 годин.
Відповідь: пліт пропливе відстань за течією за 60 годин.
Задача 26.
Катер пройшов за течією 90 км за певний час. За той самий час він пройшов би проти течії 70 км. Яку відстань за цей час пропливе пліт?
Розв’язання:
Позначимо час через tгодин. Тоді швидкість
катера за течією дорівнює ![]() 90 км , а швидкість
катера проти течії дорівнює
90 км , а швидкість
катера проти течії дорівнює
![]() 70 км . t год t
год
70 км . t год t
год
Нехай швидкість
течії ріки дорівнює х ![]() км . Відомо, що різниця
год
км . Відомо, що різниця
год
швидкостей катера за течією і проти течії дорівнює подвоєній швидкості течії ріки. Пліт рухається зі швидкістю, що дорівнює швидкості течії ріки. Запишемо:
90 70
![]() − = 2x;
− = 2x;
t t
45 35
![]() −
= x; t t
−
= x; t t
45−35 = xt; xt =10.
Але x⋅t–це відстань, яку пройде пліт за час t. Отже, пліт за час t пройде 10 км.
Відповідь: пліт за час t пройде відстань в 10 км.
Задача 27.
Круговою доріжкою завдовжки 2 км рухаються в одному напрямі два ковзанярі, які сходяться через кожні 20 хв (див. малюнок). Знайдіть швидкість кожного ковзаняра, якщо перший з них пробігає коло на 1 хв швидше, ніж другий.
Розв’язання:
![]()
Нехай перший ковзаняр пробігає коло довжиною 2км за xхвилин,
тоді швидкість його буде дорівнювати ![]() 2 км або
2 км або ![]() 2⋅60 км . x хв х год
2⋅60 км . x хв х год
Другий ковзаняр пробігає коло довжиною 2 км на 1 хвилину швидше, тобто за (х −1)хв. Отже, його швидкість
дорівнює ![]() 2 км або
2 км або ![]() 2⋅60 км . За двадцять хвилин другий
ковзаняр х −1
хв х год
2⋅60 км . За двадцять хвилин другий
ковзаняр х −1
хв х год
пробігає шлях, більший на одну довжину кола, тобто на 2 км, ніж перший ковзаняр. Запишемо:
2 2
![]() ⋅20+
2 =
⋅20+
2 = ![]() ⋅20; х х −1
⋅20; х х −1
40 40
![]() +
2 =
+
2 = ![]() ; х х
−1
; х х
−1
40+ 2х 40
![]() − = 0; х х
−1
− = 0; х х
−1
(40 + 2х)(х −1) − 40х = 0;
40х + 2х2 − 2х − 40− 40х = 0; 2х2 − 2х − 40 = 0; х2 − х − 20 = 0; D =1+80 = 81;
x1.2 ![]() ;
;
Умову задачі задовольняє
тільки додатне значення кореня, тому x =
![]() =
5. Перший ковзаняр пробігає 2 км за 5 хвилин, отже, його
=
5. Перший ковзаняр пробігає 2 км за 5 хвилин, отже, його
швидкість дорівнює: ![]() Другий пробігає 2 км
за 4
Другий пробігає 2 км
за 4
хвилини, отже, його швидкість дорівнює: ![]() 2⋅60 = 30
2⋅60 = 30 ![]() км .
км .
4 год
Відповідь: швидкість першого ковзаняра становить 24
![]() км
, а год
км
, а год
швидкість другого
становить 30 ![]() км . год Задача
28.
км . год Задача
28.
Туристи мають повернутись на базу не пізніше, як через 3 години. На яку відстань вони можуть відплисти за течією річки на
моторному човні, якщо його власна швидкість
18 ![]() км , а швидкість год
км , а швидкість год
течії річки 4 ![]() км ?
км ?
год
Розв’язання:
Швидкість човна за течією дорівнює
18+ 4 = 22 ![]() км . год
км . год
Швидкість човна проти течії дорівнює 18− 4 =14 ![]() км . Нехай
км . Нехай
год
відстань, на яку можуть відплисти туристи, дорівнює х, тоді час,
який вони витратять, пливучи за течією, дорівнює: ![]() х (год);
а час,
х (год);
а час,
22
який вони витратять, повертаючись назад, дорівнює ![]() х год. Загальний
х год. Загальний
14
час не повинен перевищувати 3 години. Отримаємо:
х х
![]() + ≤ 3;
+ ≤ 3;
22 14
11х + 7х
![]() ≤
3;
≤
3;
154
18х ≤ 462;
х ![]() ; х
; х ![]() .
.
Відповідь: туристи можуть відплисти на відстань ≈25 км.
Задача 29.
При вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння.
Розв’язання:
За першу секунду тіло проходить 4,9 м, а за кожну наступну на 9,8 м більше. Час падіння дорівнює 8 с. Отримаємо арифметичну прогресію, в якій: a1 = 4,9м, d = 9,8м, n = 8. Знайдемо, скільки метрів тіло пролетить за останню секунду:a8 = 4,9 + 7⋅9,8 = 73,5. Глибина шахти дорівнюватиме сумі всіх відстаней, які тіло пролетіло за кожну секунду, а це чисельно дорівнює сумі 8 перших членів арифметичної прогресії:
S![]()
Відповідь: глибина шахти дорівнює ≈ 314 м.
Задача 30.
Скільки секунд падала б гайка з висоти 490 м?
Розв’язання:
Із фізики відомо, що при вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше (при умові, що початкова швидкість дорівнює нулю). Отримаємо арифметичну прогресію, в якій a1 = 4,9м; d = 9,8м і Sn = 490м (оскільки всього гайка пролетіла 490 м). Нам необхідно знайти, скільки секунд падала гайка, що відповідає числу членів даної арифметичної прогресії n. Нам невідомо, скільки метрів пролетіла б гайка за останню секунду, тобто, нам невідомо, чому дорівнює an . Тому складаємо систему рівнянь:
a1 + an Sn = ![]() ⋅n;
⋅n;
2
an = a1 + (n −1)d;
4,9 + an
490 = ![]() ⋅n;
⋅n;
2
an = 4,9 + (n −1)⋅9,8;
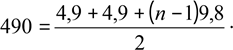 n;
n;
9,8n 2 = 980; n 2 =100; n1,2 = ±10.
Від’ємне значення кореня не задовольняє умову задачі, таким чином, n =10.
Відповідь: з висоти 490 м гайка падала б 10 с.
Задача 31.
Катер за 4 год пройшов 24 км за течією річки і 20 км проти течії. Знайдіть швидкість течії, якщо власна швидкість катера
дорівнює 12
![]() км . год
км . год
Розв’язання:
Позначимо
швидкість течії через х. Швидкість катера за течією дорівнює (12+ х)
![]() км , швидкість катера
проти течії дорівнює
км , швидкість катера
проти течії дорівнює
год
(12−
х)
![]() км . 24 км за
течією катер пройшов за
км . 24 км за
течією катер пройшов за ![]() 24 годин. 20 км год 12+ x проти течії катер
пройшов за
24 годин. 20 км год 12+ x проти течії катер
пройшов за ![]() 20 годин. Отримаємо рівняння:
20 годин. Отримаємо рівняння:
12 − x
24 20
![]() + = 4;
+ = 4;
12 + x 12 − x
6 5
![]() + −1= 0;
+ −1= 0;
12 + x 12 − x
6(12− x) +5(12+ x) −(144− x2 ) = 0; 72−6x + 60+5x −144+ x2 = 0; x2 − x −12 = 0; D =1+ 48 = 49;
![]() 1± 49
x1.2 =;
1± 49
x1.2 =;
2
Від’ємне значення кореня не задовольняє умову задачі. Таким
чином, x =
![]() =
4.
=
4.
Відповідь:
швидкість течії річки дорівнює 4 ![]() км . год
км . год
Задача 32.
З порту одночасно вийшли два теплоходи: один на південь, другий на захід. Через дві години відстань між ними становила 60 км.
Знайдіть швидкості теплоходів, якщо різниця цих швидкостей 6 ![]() км . год Розв’язання:
км . год Розв’язання:
![]() Нехай x
Нехай x ![]() км —швидкість год
км —швидкість год
першого теплохода, тоді швидкість
другого теплохода — (х +
6) ![]() км . год
км . год
Напрямки руху теплоходів перпендикулярні між собою. За 2 години перший теплохід пройшов відстань 2хкм, а другий —
2(х + 6)км. За теоремою Піфагора запишемо:
4x2 + 4(x + 6)2 = 602 ;
4x2 + 4(x2 +12x +36) = 3600;
x2 + x2 +12x +36 = 900;
2x2 +12x −864 = 0; x2 + 6x − 432 = 0;
D = 36+1728 =1764;
![]() −6 ± 1764
−6 ± 1764
x1.2 =;
2
від’ємне значення кореня не задовольняє умову задачі, тоді
x =
![]() =
=
![]() =18.
Швидкість першого теплохода дорівнює
=18.
Швидкість першого теплохода дорівнює
18 ![]() км , тоді
швидкість другого теплохода дорівнює 24
км , тоді
швидкість другого теплохода дорівнює 24 ![]() км . год год
км . год год
Відповідь: швидкість першого теплохода становить 18
![]() км , а год
км , а год
швидкість
другого теплохода становить 24 ![]() км . год
км . год
Задача 33.
З пункту А одночасно і в одному напрямі виїхали два
велосипедисти; швидкість
першого 24 ![]() км , а другого — 18
км , а другого — 18 ![]() км . Через год год
км . Через год год
годину з А виїхав автомобіль, який наздогнав спочатку другого велосипедиста, а через 10 хв і першого. Знайдіть швидкість автомобіля.
Розв’язання:
Нехай швидкість
автомобіля дорівнює х ![]() км . Через час, що год
км . Через час, що год
дорівнює t годин, він наздогнав першого велосипедиста, пройшовши при цьому відстань xt км. Перший велосипедист на цей час подолав відстань, яка дорівнює (18+18t)км. Тоді xt =18+18t.
Через ![]() 1 години 10хв =
1 години 10хв = ![]() 1 год автомобіль наздогнав другого
1 год автомобіль наздогнав другого
6 6
велосипедиста, пройшовши при цьому відстань xt + ![]() 1км.
1км.
6
Другий велосипедист за той самий час проїхав відстань, яка
дорівнює 24
+ 24t + ![]() 1км. Тоді
хt
+
1км. Тоді
хt
+ ![]() 1 = 24 + 24t +
1 = 24 + 24t + ![]() 1.
1.
6 6 6
Складаємо систему рівнянь:
хt =18+18t;
1 1 xt + ![]() 6 = 24 +
24t +
6 = 24 +
24t + ![]() 6;
6;
18
x
= ![]() t +18;
t +18;
18![]() t +18t +
t +18t + ![]() 16 = 24 + 24t + 4;
16 = 24 + 24t + 4;
3
18+ ![]() +18t + 3 = 24 + 24t + 4;
+18t + 3 = 24 + 24t + 4;
t
3
![]() +18t − 24t = 7;
+18t − 24t = 7;
t
3− 6t 2 − 7t = 0;
6t 2 + 7t −3 = 0;
D = 49 + 72 =121;
![]() − 7 ± 121
− 7 ± 121
t1,2 =
12
Від’ємне значення кореня не задовольняє умову задачі, тоді
− 7 +11 4 1
![]() t == = .
Автомобіль наздогнав першого велосипедиста
t == = .
Автомобіль наздогнав першого велосипедиста
![]() 12 3
12 3
через години. Підставимо це значення t в перше рівняння:
![]() x =18+ 6;
x =18+ 6;
![]() x = 24;
x = 24;
x = 72.
Відповідь: швидкість автомобіля дорівнює 72 ![]() км .
км .
год
Задача 34.
Виміряти питому теплоту плавлення льоду, використовуючи той факт, що швидкість теплообміну води, взятої при 0 °С, і льоду, взятого при 0°С, з повітрям однакова.
Розв’язання: τ1 θ1
![]() =
,
=
,
τ2 θ2
де τ1 – час нагрівання, τ2 - час плавлення льоду, взятого при
0°С.
θ1 = cm1(t2 −t1),θ2 =λm2,
звідси маємо:
c(t2 −t1)τ2 λ= ![]() .
.
τ1
c(t2 −t1)τ2
Відповідь: питома теплота плавлення льоду: λ= ![]() . τ1 Задача 35.
. τ1 Задача 35.
Виміряти питому теплоту плавлення льоду, використовуючи рівняння теплового балансу для випадку змішування води і льоду, температура яких різна в різних агрегатних станах. Розв’язання:
θ1 =θ2 +θ3,
θ1 = cm1∆t1 – кількість теплоти, необхідна для плавлення льоду; θ2 =λm2 – кількість теплоти, необхідна для плавлення льоду; θ3 = cm2∆t2 – кількість теплоти, необхідна для нагрівання води, отриманої із льоду;
cm1∆t1 =λm2 + cm2∆t2 , c(m1∆t1 − m2∆t2 ) λ= .
m2
.
Відповідь: питома теплота плавлення льоду рівна: c(m1∆t1 − m2∆t2) λ= .
m2
Задача 36.
Міста A,B,C,D, розміщені так, що чотирикутник ABCD – опуклий, з’єднані прямолінійними доріжками AB, BC, CD, AD і AC. Їх довжини відповідно рівні 6, 14, 5, 15 і 15 км. Із одного із цих міст одночасно вийшли три туристи, які йшли без зупинок з постійною швидкістю. Маршрути всіх туристів різні, причому кожен з них складається з трьох доріг і проходить через всі міста. Перший і другий туристи перед проходженням третіх доріг своїх маршрутів зустрілися в одному місті, а третій закінчив маршрут на годину раніше туриста, який закінчив маршрут останнім. Знайдіть швидкості туристів, якщо швидкість третього більша швидкості другого і на
1 км
![]() менша швидкості першого, причому швидкості
всіх туристів
менша швидкості першого, причому швидкості
всіх туристів
2
год знаходяться в інтервалі від 5 ![]() км до 8
км до 8 ![]() км .
км .
год год
Розв’язання:
![]()
Позначимо швидкості туристів
![]() через υ1 км ,υ2 км ,υ3 км відповідно їх год год год
через υ1 км ,υ2 км ,υ3 км відповідно їх год год год
номерам. Тоді
![]()
1) Зауважимо спочатку, що якщо у якихось туристів співпадають перші два відрізки шляху, то повинні повністю співпадати їх маршрути. За умовою кожен маршрут складається із трьох відрізків і проходить через всі чотири міста. За умовою всі маршрути різні. Значить, можна зробити висновок, що у двох будь-яких туристів шляхи відрізняються уже після проходження перших двох доріг.
2) Якщо туристи вийшли із міста А, то хто-небудь з них повинен йти по діагоналі АС, але тоді він не зможе пройти через всі чотири міста (його маршрут складається тільки з трьох відрізків). Тобто, туристи не могли вийти з міста А. З аналогічних причин не могли вони вийти із міста С. Тобто, туристи вийшли з міста В чи з міста D.
3)
![]()
![]() За умовою перший і другий туристи зустрілись
перед проходженням третіх доріг, тому перший і другий туристи вийшли по різних дорогах
і зустрілись в протилежній вершині чотирикутника. Оскільки υ1 >υ2 , то довжина шляху першого
туриста до зустрічі з другим рівна AB +
AD = 21,
а довжина шляху другого до тієї ж зустрічі рівна BC + CD =19. Отримаємо рівняння: 21 = 19.
За умовою перший і другий туристи зустрілись
перед проходженням третіх доріг, тому перший і другий туристи вийшли по різних дорогах
і зустрілись в протилежній вершині чотирикутника. Оскільки υ1 >υ2 , то довжина шляху першого
туриста до зустрічі з другим рівна AB +
AD = 21,
а довжина шляху другого до тієї ж зустрічі рівна BC + CD =19. Отримаємо рівняння: 21 = 19.
υ1 υ2
4) Другий відрізок шляху третього туриста співпадає з АС, а довжина всього шляху рівна або
![]() BC + CA + AD = 44, чи
BC + CA + AD = 44, чи
![]() AB
+ AC + CD = 26.
AB
+ AC + CD = 26.
В першому випадку шлях третього туриста
найдовший. Оскільки υ1 >υ3 , то перший турист прийшов
раніше третього. Довжина шляху другого туриста не перевищує 34 км, значить,
час його руху не більше ![]() , а час третього рівний
, а час третього рівний ![]() . Маємо
. Маємо
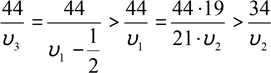 .
.
В першому випадку третій турист повинен прийти в кінцевий пункт останнім, але це суперечить умові задачі. Тобто, довжина шляху третього туриста рівна не 44 км, а 26 км.
5) Нехай туристи вийшли із міста В. Тоді шлях першого – BADC, шлях другого – BCDA, шлях третього – BACD. Довжини шляхів рівні відповідно 26 км, 34 км, 26 км, а час, затрачений на всю дорогу,
рівний 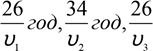 год. Із п.3) випливає, що перший турист
год. Із п.3) випливає, що перший турист
![]() закінчив
маршрут раніше, ніж другий υ261 <υ342 .
Використовуючи
закінчив
маршрут раніше, ніж другий υ261 <υ342 .
Використовуючи
умову, знаходимо ![]() =1+
=1+![]() ; оскільки υ3 ≤ 8, то
; оскільки υ3 ≤ 8, то 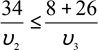 , чи
, чи
υ3 ≤υ2 , що суперечить умові.
Отже, туристи вийшли з міста D, шлях першого – DABC, другого – DCBA, третього – DCAB. Довжини шляхів рівні відповідно 35 км, 25 км, 26 км, а час на всю дорогу рівний
 год.
год.
35 25
|
υ υ |
||
|
Отримаємо систему рівнянь: 35 26 υ υ1 −υ3 = 2 |
1 |
2 |
|
звідки
|
Корені |
цього |
![]() Із
п.3) слідує, що останнім прийшов перший турист > .
Із
п.3) слідує, що останнім прийшов перший турист > .
υ1 υ1 − ![]() 1 2 1 2
1 2 1 2
рівняння рівні 7 і ![]() . За умовою, швидкості розміщені в проміжку від
. За умовою, швидкості розміщені в проміжку від
5 до 8 кілометрів, значить, другий корінь не підходить. Тобто, υ1 = 7,
![]() ,
,
.
Легко перевірити, що знайдені значення швидкостей задовольняють всім умовам задачі.
Відповідь: швидкість першого туриста становить 7
![]() км , год
км , год
швидкість другого туриста становить 6![]() 1 км , швидкість третього
1 км , швидкість третього
3 год
туриста становить 6![]() 1 км . 2 год
1 км . 2 год
Задача 37.
Із пункту А в пункт В доставлена
пошта. Спочатку її віз мотоцикліст; проїхавши ![]() відстані від пункту А
до пункту В, передав пошту велосипедисту, який на нього чекав і який доставив
її в пункт В (час, який потрібний був на передачу пошти, вважається рівним
нулю). При цьому пошта була доставлена із пункту А в пункт В за проміжок
часу, необхідний, щоб проїхати від пункту А до пункту В з швидкістю
40
відстані від пункту А
до пункту В, передав пошту велосипедисту, який на нього чекав і який доставив
її в пункт В (час, який потрібний був на передачу пошти, вважається рівним
нулю). При цьому пошта була доставлена із пункту А в пункт В за проміжок
часу, необхідний, щоб проїхати від пункту А до пункту В з швидкістю
40 ![]() км . Відомо, що якби
мотоцикліст і велосипедист год
км . Відомо, що якби
мотоцикліст і велосипедист год
виїхали із пунктів А і В одночасно назустріч один одному, то вони зустрілися б через проміжок часу, який необхідний для проїзду від
пункту А
до пункту В з швидкістю 100 ![]() км . Знайдіть швидкість год
км . Знайдіть швидкість год
мотоцикліста, враховуючи, що вона більша швидкості велосипедиста. Розв’язання:
Позначимо через S км відстань між пунктами А
і В; нехай x ![]() км год
км год
– швидкість мотоцикліста, а у ![]() км – швидкість велосипедиста.
год
км – швидкість велосипедиста.
год
![]() Нехай
Нехай
![]() 2 S км мотоцикліст
проїхав за 2 ⋅
S
годин, а шлях
2 S км мотоцикліст
проїхав за 2 ⋅
S
годин, а шлях ![]() 1 S км
1 S км
3 3 x 3
![]() велосипедист
проїхав за 1⋅
S
годин. Пошта із А в В була доставлена
велосипедист
проїхав за 1⋅
S
годин. Пошта із А в В була доставлена
3 y
![]() за
2 ⋅ S + 1 ⋅ S годин, і цей час за умовою
задачі повинен
за
2 ⋅ S + 1 ⋅ S годин, і цей час за умовою
задачі повинен
3 x 3 y
дорівнювати ![]() S годин. Тому маємо перше рівняння
S годин. Тому маємо перше рівняння
40
2
![]() S 1
S S ⋅ + ⋅ = .
S 1
S S ⋅ + ⋅ = .
3 x 3 y 40
Якби мотоцикліст і велосипедист виїхали назустріч один
одному, то вони зустрілися б через ![]() S годин, і цей час за
умовою x + y
S годин, і цей час за
умовою x + y
задачі повинен дорівнювати ![]() S годин. Тому маємо друге
рівняння
S годин. Тому маємо друге
рівняння
100
S S
![]() = .
x + y 100
= .
x + y 100
Для знаходження х і у отримали після ділення правої і лівої частини кожного рівняння на S (S ≠ 0) систему
2 1 1 1 1
![]() 3
⋅ x + 3⋅ y = 40,
3
⋅ x + 3⋅ y = 40,
![]() 1 = 1 .
1 = 1 .
x + y 100
Із другого рівняння y =100− x. Підставляючи 100− x замість y в перше рівняння системи, отримаємо рівняння:
2 1 1
![]() + = ,
+ = ,
3x 3(100− x) 40
яке має корені x1 =
80,x2 = ![]() . Але тоді y1 = 20 і y2 =
. Але тоді y1 = 20 і y2 = ![]() .
.
Легко побачити, що знайдені пари чисел
x1 = 80,
y1 = 20,
x2
= ![]() ,
,
y2 =
![]() .
.
є розв’язками системи рівнянь.
Оскільки за умовою задачі швидкість мотоцикліста більша швидкості велосипедиста, то умову задачі задовольняє лише один розв’язок системи, тобто: x.1 = 80, y1 = 20. Отже, швидкість
мотоцикліста рівна 80 ![]() км . год
км . год
Відповідь: швидкість мотоцикліста становить 80 ![]() км . год
км . год
Задача 38.
Із пункту А в пункт В виїхав вантажний автомобіль. Через одну годину із пункту А в пункт В виїхав легковий автомобіль, який прибув в пункт В одночасно з вантажним автомобілем. Якби вантажний і легковий автомобілі одночасно виїхали з пунктів А і В назустріч один одному, то вони б зустрілися через 1 годину 12 хвилин після виїзду. Скільки часу провів у дорозі від А до В вантажний автомобіль?
Розв’язання:
Позначимо через
x ![]() км швидкість вантажного
автомобіля, а год
км швидкість вантажного
автомобіля, а год
через S км – відстань між пунктами А і В.
Відстань від А до В вантажний автомобіль проїхав за ![]() S годин, а легковий автомобіль
– за x
S годин, а легковий автомобіль
– за x
S
![]() −1 годин. Тобто, швидкість
легкового автомобіля рівна
−1 годин. Тобто, швидкість
легкового автомобіля рівна
x
S км
![]() . Якби автомобілі одночасно виїхали
із пунктів А і В S −1
год x
. Якби автомобілі одночасно виїхали
із пунктів А і В S −1
год x
назустріч один одному, то із умови, що вони зустрінуться через
1![]()
години, отримаємо рівняння:
1![]() 1x + S = S.
1x + S = S.
![]() 5 S −1
5 S −1
x
Оскільки x〉0, то, розділивши це рівняння на х, отримаємо рівносильне йому рівняння:
S
![]()
![]() 61+ x =
61+ x = ![]() S .
S .
5 ![]() S −1 x
S −1 x
x
Позначимо ![]() S через t, приходимо
до рівняння 5t 2 −17t + 6 = 0, x
S через t, приходимо
до рівняння 5t 2 −17t + 6 = 0, x
яке має корені t1 =
3,t2 = ![]() . Із умови задачі відомо,
що вантажний автомобіль провів в дорозі від А до В більше однієї години,
тобто, умову задачу задовольняє тільки t1 =
3.
. Із умови задачі відомо,
що вантажний автомобіль провів в дорозі від А до В більше однієї години,
тобто, умову задачу задовольняє тільки t1 =
3.
Відповідь: вантажний автомобіль провів у дорозі від А до В 3 год.
Задача 39.
Від пристані А вниз за течією річки одночасно відпливли теплохід і пліт. Теплохід, допливши до пристані В, яка розміщена в 324 км від пристані А, простояв там 18 годин і відправився назад в А.
В той момент, коли він знаходився в 180 км від А, другий теплохід, який відплив із А на 40 годин пізніше першого, наздогнав пліт, який до цього часу встиг пропливти 144 км. Вважаючи, що швидкість течії річки стала, швидкість плоту рівна швидкості течії ріки, а швидкості теплоходів в стоячій воді сталі і рівні між собою, визначте швидкості теплоходів і течії річки.
Розв’язання:
Позначимо швидкості теплоходів через
x ![]() км , а швидкість течії
год
км , а швидкість течії
год
річки через у ![]() км . Час, який пройшов
від моменту відплиття плоту год
км . Час, який пройшов
від моменту відплиття плоту год
від пристані А до того моменту, коли його наздогнав другий
теплохід, рівний 144![]() годин.
Другий теплохід до моменту зустрічі з плотом y
годин.
Другий теплохід до моменту зустрічі з плотом y
знаходився в дорозі ![]() 144 годин (він плив за течією,
і, значить, його x +
y
144 годин (він плив за течією,
і, значить, його x +
y
швидкість відносно
берегів рівна (x
+ y)
![]() км ). Із умови задачі
відомо, год
км ). Із умови задачі
відомо, год
що справджується рівність
144 144
![]() −
= 40. у х +
у
−
= 40. у х +
у
За час 144![]() годин перший теплохід встиг
пропливти 324 км за у
годин перший теплохід встиг
пропливти 324 км за у
течією з швидкістю
(х
+ у)
![]() км відносно берегів,
простояти в пристані год
км відносно берегів,
простояти в пристані год
В 18 годин і пропливти 324км −180км =144км проти течії річки, рухаючись
відносно берегів з швидкістю (х − у)
![]() км . Отже, має місце
год
км . Отже, має місце
год
рівність:
144 324 144
![]() =
+18+
=
+18+ ![]() . у
х + у х − у
. у
х + у х − у
![]() Для
знаходження х і у маємо систему рівнянь 144 −
144 = 40 і
Для
знаходження х і у маємо систему рівнянь 144 −
144 = 40 і
у х + у
144 324 144 5y2
![]() = +18+
= +18+ ![]() . З першого
рівняння знаходимо: x =
. З першого
рівняння знаходимо: x = ![]() .
.
у х + у х − у 18−5y
Підставляючи ![]() 5y2 замість х в друге рівняння, розділимо
його
5y2 замість х в друге рівняння, розділимо
його
18−5y
обидві частини на 18, отримаємо рівняння:
8 18−5у 4(18 −5у)
![]() = +1+
2 , у
у 5у −9у
= +1+
2 , у
у 5у −9у
10у 2 −33у + 9 = 0.
Це квадратне рівняння має два корені: y1 = ![]() , y2 = 3. Відповідні значення
х рівні: x1
=
, y2 = 3. Відповідні значення
х рівні: x1
= ![]() , x2 =15. Видно, що пари чисел
, x2 =15. Видно, що пари чисел
3 3
x1 = ![]() , y1 =
, y1 = ![]() і x2 =15, y2 = 3 є розв’язками системи
рівнянь
і x2 =15, y2 = 3 є розв’язками системи
рівнянь
144144 324 144
![]()
![]()
![]() − = 40, = +18+
− = 40, = +18+ ![]() . Із умови
задачі випливає, що у х +
у у х + у
х − у х > y. Цій нерівності
відповідає тільки другий розв’язок системи.
. Із умови
задачі випливає, що у х +
у у х + у
х − у х > y. Цій нерівності
відповідає тільки другий розв’язок системи.
Відповідь: швидкості теплоходів становлять 15 ![]() км , швидкість год
км , швидкість год
течії річки
становить 3 ![]() км . год
км . год
Задача 40.
Із міста А в місто В виїхав автомобіль. Одночасно з ним із пункту С, який розміщений між А і В, в місто А виїхав другий автомобіль. Перший прибув в В одночасно з прибуттям другого в А. Потім автомобілі одночасно виїхали назустріч один одному, зустрілись в пункті D і одночасно прибули перший в А, другий в В. Кожний автомобіль їхав з своєю постійною швидкістю, але другий зробив зупинку на шляху від С до А, а перший – зупинку тієї ж тривалості на шляху від В до D. Знайдіть відстань між С і D, якщо відомо, що відстань від А до С рівна 270 км, а відстань від С до В рівна 180 км.
Розв’язання:
Позначимо через х км відстань від пункту А до пункту D. Із умови задачі випливає, що відстань між пунктами А і В рівна (270+180)= 450км, а між пунктами В і D рівна (450− х)км. Перший автомобіль до зустрічі з другим автомобілем проїхав відстань від пункту А до пункту В, рівну 450 км, а потім відстань від пункту В до пункту D, рівну (450− х)км, тобто всього (900− х)км. Другий автомобіль до зустрічі з першим проїхав шлях від С до А довжиною в 270 км, а також шлях від А до D, довжиною в х км, тобто всього (270+ x)км. На шляху до пункту D кожен із них зробив зупинку однієї і тієї ж тривалості. Значить, в русі до пункту D автомобілі знаходились один і той же час. Тому відношення швидкості першого автомобіля до швидкості другого автомобіля рівне відношенню
пройдених відстаней, тобто ![]() 900− x.
900− x.
270+ x
Після зустрічі автомобілі рухались не зупиняючись. Перший з них пройшов відстань AD, рівну х км, а другий – відстань DB, рівну (450− x)км. Виїхали з D автомобілі одночасно і в кінцеві пункти
прибули одночасно. Тому відношення їх швидкостей рівне: ![]() x .
x .
450− x
![]() Оскільки
швидкості автомобілів постійні, то: 900− x = x ,
Оскільки
швидкості автомобілів постійні, то: 900− x = x ,
270+ x 450− x
звідки x = 250. Оскільки відстань від А до С рівна 270 км, а відстань від А до D рівна 250 км, то шукана відстань між D і С рівна 20 км. Відповідь: відстань між С і D становить 20 км.
Задача 41.
В річку впадає притока. Теплохід відходить
від пристані А на притоці, йде вниз за течією 80 км до річки, далі
по річці вверх проти течії до пристані В, затративши 18 годин на весь шлях
від А до В. Потім теплохід повертається назад. Час руху по тому ж
шляху від В до А рівний 15 годинам. Власна швидкість теплохода, тобто
швидкість теплохода в стоячій воді, рівна 18 ![]() км . Швидкість течії
год
км . Швидкість течії
год
річки рівна 3 ![]() км . Яка відстань від
пристані А до пристані В і яка год
км . Яка відстань від
пристані А до пристані В і яка год
швидкість притоки?
Розв’язання:
Позначимо через υкм швидкість притоки, а через у км – год
відстань по ріці від місця впадання притоки в ріку до пункту В.
На рух вниз по притоці теплохід затратив ![]() годин, а на рух по річці до
пристані В затратив
годин, а на рух по річці до
пристані В затратив ![]() y годин. Оскільки на цей шлях теплохід
y годин. Оскільки на цей шлях теплохід
15
![]() всього затратив 18 годин, то 80 +
y =18. На рух назад теплохід
υ+18 15
всього затратив 18 годин, то 80 +
y =18. На рух назад теплохід
υ+18 15
затратив по річці ![]() y годин, а по притоці
y годин, а по притоці ![]() 80 годин, що складає 15
80 годин, що складає 15
21 18−υ
![]() годин, звідси y + 80 =15.
годин, звідси y + 80 =15.
21 18−υ
Із рівності
80 у
![]() +
=18 υ+18 15
+
=18 υ+18 15
маємо:
80
y =1518− ![]() , υ+18
, υ+18
тобто y ![]() . Підставляючи
. Підставляючи ![]() замість y в
замість y в
рівність ![]()
![]() , отримаємо рівняння для знаходження
υ:
, отримаємо рівняння для знаходження
υ:
10 9υ+122 80
![]() ⋅ + =15.
⋅ + =15.
7 υ+18 −υ+18
Оскільки за умовою задачі 0 <υ<18, то це рівняння рівносильне рівнянню υ2 + 64υ−132 = 0, яке має два корені: υ1 = 2 і υ2 = −66. В проміжок 0 <υ<18 попадає лише один із них, а тому
км υ1 =
2. Значить, швидкість притоки 2 ![]() . Оскільки відстань між
год
. Оскільки відстань між
год
пристанями А і В рівна s = 80+ y, тобто, s
![]() ,
то
,
то
підставляючи в цю рівність υ= 2, отримаємо, що s = 290км.
Відповідь: відстань від пристані А
до пристані В рівна 290 км; швидкість притоки становить 2 ![]() км . год
км . год
Задача 42.
Із двох пунктів, відстань між якими рівна 2400 км, назустріч один одному виїжджають одночасно пасажирський і швидкий потяги. Кожен із них йде з постійною швидкістю, і в деякий момент часу вони зустрічаються. Якби два потяги їхали зі швидкістю швидкого потяга, то їх зустріч відбулася б на три години раніше фактичного моменту зустрічі. Якби два потяги їхали зі швидкістю пасажирського потяга, то їх зустріч відбулася б на п’ять годин пізніше фактичного часу зустрічі. Знайдіть швидкості потягів.
Розв’язання:
Позначимо швидкості пасажирського і швидкого потягів
відповідно через
υп ![]() км і υш
км і υш ![]() км . Тоді час, який пройшов
від моменту год год
км . Тоді час, який пройшов
від моменту год год
виходу потягів із початкових пунктів до їх зустрічі, рівний
2400 ![]() годин.
Якби два потяги їхали зі швидкістю υш, то час руху
годин.
Якби два потяги їхали зі швидкістю υш, то час руху
υп +υш
складав би ![]() 2400годин. Таким чином, отримуємо
рівняння: 2υш
2400годин. Таким чином, отримуємо
рівняння: 2υш
2400 2400
![]() − = 3. υп +υш 2υш
− = 3. υп +υш 2υш
Аналогічно складається друге рівняння:
![]() 2400
2400
− ![]() = 5. υп +υш
= 5. υп +υш
Після спрощення отримуємо систему:
![]() υш −υп 1
υш −υп 1
υш(υп +υс ) = 400,
![]() υш −υп = 1 .
υш −υп = 1 .
υп(υп +υш ) 240
Почленно розділивши друге рівняння системи на перше, υш 5 5 5 знаходимо,
що = ![]() , чи υш =
υп. Підставивши υп замість υшв υп 3 3 3
, чи υш =
υп. Підставивши υп замість υшв υп 3 3 3
друге рівняння системи, отримаємо, що υп = 60. Але тоді υш =100.
Відповідь: швидкість пасажирського потяга рівна 60
![]() км , год
км , год
швидкість швидкого
потяга 100 ![]() км . год
км . год
Задача 43.
Із пункту А в
пункт В відправився швидкий потяг. Одночасно назустріч йому із В в
А вийшов товарний потяг, який зустрівся з швидким через ![]() години після відправлення.
Відстань між пунктами
години після відправлення.
Відстань між пунктами
А і В рівна 80 км, потяги рухались з постійними
швидкостями. З якою швидкістю рухався швидкий потяг, якщо 40 км він йшов
на ![]() години
години
довше, ніж товарний потяг йшов 5 км?
Розв’язання:
Позначимо швидкості товарного і швидкого потягів відповідно
через υт ![]() км і υш
км і υш ![]() км . Тоді за
км . Тоді за ![]() 2години товарний потяг проїде
2υткм, год год 3 3
2години товарний потяг проїде
2υткм, год год 3 3
![]() а швидкий 2υшкм. Оскільки через години потяги зустрінуться
і так
а швидкий 2υшкм. Оскільки через години потяги зустрінуться
і так
3
як відстань між пунктами рівна 80 км, то
2 2
υт + υш = 80
3 3
Сорок кілометрів швидкий потяг проїде за t1 =
![]() 40 години, а υш
40 години, а υш
товарний потяг 5 км пройде за t2 =![]() години. Оскільки t1〉t2 на
години. Оскільки t1〉t2 на
![]() години, то
години, то
40 5 3
![]() − = .
− = .
υш υт 8
Для знаходження швидкостей потягів отримали систему рівнянь
![]() 23(υт +υш )= 80,
23(υт +υш )= 80,
![]() 40 − 5 = 3.
40 − 5 = 3.
υш υт 8
Із першого рівняння цієї системи знаходимо: υт =120−υш.
Підставивши 120−υш замість υт в друге рівняння системи, отримаємо рівняння:
![]() 40 5
40 5
![]() − =,
υш 120−υш
− =,
υш 120−υш
яке можна переписати у вигляді:
![]() 3υш2 −720υш +38400 = 0.
3υш2 −720υш +38400 = 0.
8υш (120−υш )
Останнє рівняння має корені υш(1) = 80,υш(2) =160, але тоді із υт =120−υш знаходимо, що υт(1) = 40, а υт(2) = −40. Таким чином, система має два розв’язки: υш(1) = 80,υт(1) = 40 і υш(2) =160,υт(2) = −40. Оскільки швидкість потяга не може бути від’ємним числом, то умову задачі задовольняє лише перша пара чисел. Отже, швидкість
швидкого потяга 80 ![]() км . год
км . год
Відповідь: швидкість швидкого потягу становить 80
![]() км . год
км . год
Задача 44.
Вантажівка і автомобіль виїхали одночасно із пункту А і повинні прибути в пункт С. Вантажівка, рухаючись з постійною швидкістю, доїхала до пункту С, проїхавши шлях, рівний 360 км. Автомобіль поїхав по окружній дорозі і спочатку доїхав до пункту В, розміщеного в 120 км від пункту А, рухаючись зі швидкістю, вдвічі більшою швидкості вантажівки. Після пункту В він збільшив свою швидкість
на 40 ![]() км і проїхав шлях від
пункту В до пункту С, рівний 1000 км. год
км і проїхав шлях від
пункту В до пункту С, рівний 1000 км. год
Він прибув в пункт С на 1 годину 15 хвилин пізніше вантажівки. Якби автомобіль весь свій шлях від пункту А до пункту С їхав з тією ж швидкістю, що й від пункту В до пункту С, то в пункт С він прибув би на 1 годину пізніше вантажівки. Знайдіть швидкість вантажівки. Розв’язання:
Позначимо швидкість вантажівки через
x ![]() км ; тоді швидкість год
км ; тоді швидкість год
автомобіля на ділянці АВ рівна
2х ![]() км , а на ділянці ВС
рівна год
км , а на ділянці ВС
рівна год
(2х + 40)
![]() км . Автомобіль на шлях
між пунктами А і С затратив год
км . Автомобіль на шлях
між пунктами А і С затратив год
120 1000 360
![]() + годин,
а вантажівка проїхала свій шлях за
+ годин,
а вантажівка проїхала свій шлях за ![]() годин.
годин.
x 2x + 40 x
Оскільки час руху вантажівки на ![]() години менший часу руху
години менший часу руху
автомобіля, то
120 1000 360 5
![]() + − = .
+ − = .
2x 2x + 40 x 4
Якби автомобіль весь свій шлях від пункту А
до пункту С їхав зі швидкістю (2x + 40)
![]() км , то йому для цього
знадобилося б
км , то йому для цього
знадобилося б ![]() 1120 год 2х
+ 40
1120 год 2х
+ 40
годин, що за умовою на одну годину більше часу руху вантажівки. Тому
![]() 1120 360 − =1.
1120 360 − =1.
2х + 40 х
Для знаходження значення х отримали систему двох рівнянь з одним невідомим:
120 1000 360 5
![]() 2x + 2x + 40 − x = 4,
2x + 2x + 40 − x = 4,
![]() 21120x
+ 40 − 360x =1.
21120x
+ 40 − 360x =1.
Для її розв’язання достатньо розв’язати, наприклад, перше рівняння і вибрати із найдених розв’язків числа, які задовольняють друге рівняння. Перше рівняння рівносильне рівнянню:
x2 −140x + 4800 = 0,
яке має корені x1 = 80 і x2 = 60. Підставляючи x1 і x2 в друге рівняння, отримаємо, що його задовольняє лише x2 . Тому швидкість
вантажівки рівна 60 ![]() км . год
км . год
Відповідь:
швидкість вантажівки становить 60 ![]() км . год
км . год
Задача 45.
Теплохід відчалив від пристані А, спустився
вниз за течією річки на 60 км до гирла річки, яка впадає в притоку і піднявся
верх по притоці (проти течії) на 20 км до пристані В. Весь шлях від
А до В теплохід пройшов за 7 годин. Швидкість течії річки і швидкість
течії притоки рівна 1 ![]() км . Знайти власну швидкість теплохода. (Власна
год
км . Знайти власну швидкість теплохода. (Власна
год
швидкість – швидкість в нерухомій воді).
Розв’язання:
Позначимо через x ![]() км власну швидкість
теплохода. Тоді по год
км власну швидкість
теплохода. Тоді по год
річці теплохід йшов з швидкістю (х
+1)
![]() км , а по притоці – з
год
км , а по притоці – з
год
швидкістю (х −1)
![]() км . На шлях по річці
теплохід затратив
км . На шлях по річці
теплохід затратив ![]() 60 годин, год х +1
60 годин, год х +1
а на шлях по притоці
![]() 20 годин. Весь шлях він пройшов
за 7 годин, х −1
20 годин. Весь шлях він пройшов
за 7 годин, х −1
значить,
60 20
![]() + = 7.
+ = 7.
х +1 х −1
Звільняючись в цьому рівнянні від знаменника, отримуємо
рівняння 7х2 −80х
+33 = 0, корені якого х1 =11 і х2 = ![]() 3. Ми бачимо, 7
3. Ми бачимо, 7
![]() що ці корені являються й коренями рівняння:
60 +
20 = 7. х +1 х −1
що ці корені являються й коренями рівняння:
60 +
20 = 7. х +1 х −1
![]() Швидкість теплохода не може
бути меншою 1
Швидкість теплохода не може
бути меншою 1 ![]() км ,оскільки теплохід
год
км ,оскільки теплохід
год
рухався по притоці проти течії, швидкість якої рівна 1 ![]() км . Тому год
км . Тому год
власна швидкість теплохода 11 ![]() км . год
км . год
Відповідь: власна швидкість теплохода становить 11 ![]() км . год
км . год
Задача 46.
Пункт А стоїть в полі на відстані 8 км від дороги. На дорозі, яка являється прямою лінією, стоїть пункт В. Швидкість руху автомобіля по дорозі в два рази більша, ніж по полю. Відомо, що якщо їхати із А по прямій до деякої точки С, яка знаходиться на дорозі, відмінної від В, а потім по дорозі до В, то при довільному виборі точки С на це піде не менше часу, ніж потрібно, якщо їхати із А в В напрямки по полю.
Чому рівна відстань від А до В?
Розв’язання:
Позначимо через а км відстань між пунктами
А і В (зрозуміло, що a ≥ 8), через υкм – швидкість год
руху автомобіля по полю і через D – точку на дорозі, найменш віддалену від пункту А (мал.12).
Тоді AD ⊥ BD і AD = 8 км. Очевидно, що якщо точки В і D співпадають, тобто, якщо AB = 8 км, то умова задачі виконується. Значить, AB = 8 км є однією із відповідей до задачі. Далі будемо вважати, що точки В і D різні, тобто a〉8, і пункт В лежить ліворуч від прямої АD, якщо дивитися із точки D в поле в напрямку до пункту А.
Два довільних розміщення пункту В на дорозі, симетричні відносно прямої АD, одночасно чи задовольняють умову задачі чи не задовольняють. Нехай точка С лежить на відрізку ВD і відмінна від точки В. Позначимо через х км відстань між точками А і С. Тоді 8 ≤ x〈a, і час, за який автомобіль проїде шлях АСВ, рівний:
![]() AC BC x a2 −64 − x2 −64
AC BC x a2 −64 − x2 −64
+ = + . υ 2υ υ 2υ
За умовою для всіх х із інтервалу 8 ≤ x〈a справедлива нерівність
x a2 −64 − x2 −64 a
+ ≥ ,
υ 2υ υ
2(x − a)+ a2 −64 ≥ x2 −64.
![]()
![]() Доведемо, що якщо при деякому а
(a〉8)
множина розв’язків нерівності 2(x − a)+ a2 −64 ≥ x2 −64 містить інтервал
8 ≤ x〈a, то пункт В,
що знаходиться на дорозі, віддалений від пункту А на відстань а км,
задовольняє умову задачі. Нехай АВ =
а за сформульованою вище умовою. Якщо точка С лежить на прямій
ВD ліворуч точки В (точка C1 на мал.35), то АС > AB і значить,
рух по шляху АСВ займає більше часу, ніж по
Доведемо, що якщо при деякому а
(a〉8)
множина розв’язків нерівності 2(x − a)+ a2 −64 ≥ x2 −64 містить інтервал
8 ≤ x〈a, то пункт В,
що знаходиться на дорозі, віддалений від пункту А на відстань а км,
задовольняє умову задачі. Нехай АВ =
а за сформульованою вище умовою. Якщо точка С лежить на прямій
ВD ліворуч точки В (точка C1 на мал.35), то АС > AB і значить,
рух по шляху АСВ займає більше часу, ніж по
![]()
![]() Тоді нерівність
Тоді нерівність
. Але це
![]() означає,
що рух по шляху АСВ займе не менше часу, ніж по шляху АВ. Якщо точка
С лежить на прямій ВD праворуч від точки D (точка C2 на мал.35), то AC〉 AD і BC〉 BD. Тобто, рух
по шляху АСВ в цьому випадку займе більше часу, ніж рух по шляху АВ.
Отже, сформульоване вище твердження доведено.
означає,
що рух по шляху АСВ займе не менше часу, ніж по шляху АВ. Якщо точка
С лежить на прямій ВD праворуч від точки D (точка C2 на мал.35), то AC〉 AD і BC〉 BD. Тобто, рух
по шляху АСВ в цьому випадку займе більше часу, ніж рух по шляху АВ.
Отже, сформульоване вище твердження доведено.
Умову задачі задовольняють ті і тільки ті із точок В, відмінні від
D, для яких при а = АВ множина розв’язків нерівності
![]() 2(x
− a)+ a2 −64 ≥ x2 −64 містить інтервал
8 ≤ x〈a. Нехай а
– довільне фіксоване число таке, що a〉8.
Знайдемо розв’язки нерівності(2(x − a)+ a2 −64 ≥ x2 −64), які знаходяться
в області
2(x
− a)+ a2 −64 ≥ x2 −64 містить інтервал
8 ≤ x〈a. Нехай а
– довільне фіксоване число таке, що a〉8.
Знайдемо розв’язки нерівності(2(x − a)+ a2 −64 ≥ x2 −64), які знаходяться
в області
![]() 8
≤ x〈a. В цій області
нерівність (2(x
− a)+ a2 −64 ≥ x2 −64) рівносильна
системі нерівностей:
8
≤ x〈a. В цій області
нерівність (2(x
− a)+ a2 −64 ≥ x2 −64) рівносильна
системі нерівностей:
![]() 2(x
− a)+ a2 −64 ≥ 0,
2(x
− a)+ a2 −64 ≥ 0,
(2(x − a)+ a2 −64)2 ≥ x2 −64.
Отриману систему нерівностей можна після перетворень замінити рівносильною їй системою, яка має вигляд:
1 2
![]() x ≥ a − a −64,
x ≥ a − a −64,
2
![]() (x
− a)(3x
−5a + 4 a2 −64)≥ 0.
(x
− a)(3x
−5a + 4 a2 −64)≥ 0.
Остання система нерівностей на множині 8 ≤ x〈a рівносильна системі:
1 2
x ≥ a − a −64,
2
![]() 3x −5a + 4 a2 −64 ≤ 0,
3x −5a + 4 a2 −64 ≤ 0,
яку можна переписати у вигляді подвійної нерівності:
a ![]() .
.
Для шуканих значень а весь інтервал 8 ≤ x〈a повинен міститися
в множині a ![]() . Тобто, шукані значення
. Тобто, шукані значення
параметра а являються розв’язками системи нерівностей:
1 2
![]() a − 2 a −64 ≤ 8,
a − 2 a −64 ≤ 8,
5a 4 2
![]() a ≤ − a −64,
a ≤ − a −64,
3 3
a〉8.
Ця система після перетворення може бути переписана так:
![]() 2a −16 ≤ a2 −64,
2a −16 ≤ a2 −64,
2
2 a −64 ≤ a,
a〉8.
На множині a〉8 ліва і права частина першої і другої нерівності невід’ємні, тому ця система нерівностей рівносильна системі:
(2a −16)2 ≤ a2 −64,
2 2
4(a −64)≤ a ,
a〉8
або 3a2 −64a +320 ≤ 0,
2
3a − 256 ≤ 0,
a〉8.
Множина розв’язків першої нерівності системи є інтервалом
![]() , а множина розв’язків другої – інтервал –
, а множина розв’язків другої – інтервал – ![]() . Тому множина розв’язків
системи, а значить, і множина розв’язків задачі є інтервал
. Тому множина розв’язків
системи, а значить, і множина розв’язків задачі є інтервал ![]() . Додаючи сюди знайдене
раніше значення a =
8, отримуємо відповідь до задачі.
. Додаючи сюди знайдене
раніше значення a =
8, отримуємо відповідь до задачі.
Відповідь: відстань від
А до В рівна 8км ≤
АВ 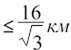 .
Задача 47.
.
Задача 47.
Відстань між двома містами швидкий потяг проходить
на 4 години швидше товарного і на 1 годину швидше пасажирського. Відомо, що швидкість
товарного потяга складає ![]() швидкості пасажирського і на 50
швидкості пасажирського і на 50 ![]() км менша швидкості швидкого.
Знайдіть год
км менша швидкості швидкого.
Знайдіть год
швидкості товарного і швидкого потягів.
Розв’язання:
Позначимо швидкість товарного потягу через x ![]() км . Тоді із год
км . Тоді із год
умови задачі слідує, що
швидкості пасажирського і швидкого потягів рівні відповідно ![]() 8x км і (х
+50)
8x км і (х
+50)
![]() км . Якщо відстань між
містами
км . Якщо відстань між
містами
5 год год
рівна S км, то час, за який товарний, пасажирський і швидкий потяги
пройдуть цю відстань, рівний відповідно: ![]() S годин, S годин,
S годин, S годин, ![]() S
S
![]() x 8x x
+50
x 8x x
+50
5
годин. Із умови задачі випливає справедливість рівностей:
S S
![]() x − x +50 = 4,
x − x +50 = 4,
![]() 58Sx
− x +S50 =1.
58Sx
− x +S50 =1.
Отриману систему рівнянь можна переписати так:
50S
![]() x(x
+50)
= 4,
x(x
+50)
= 4,
S(250−3x) =1.
8x(x +50) Розділивши почленно перше рівняння системи на друге, отримаємо рівняння:
400
![]() = 4, 250−3x
= 4, 250−3x
звідки x = 50.
Відповідь: швидкість товарного потяга рівна 50 ![]() км і швидкого год
км і швидкого год
потяга рівна
100 ![]() км . год Задача
48.
км . год Задача
48.
Автомобіль їхав вгору. В першу секунду після досягнення пункту А він проїхав 30 м, а в кожну наступну секунду він проїжджав на 2 м менше, ніж в попередню. Через 9 с після того, як автомобіль досяг пункту А, назустріч йому виїхав автобус із пункту В, який знаходиться на відстані 258 м від пункту А. В першу секунду автобус проїхав 2 м, а в кожну наступну секунду він проїжджав на 1 м більше, ніж в попередню. Яку відстань проїхав автобус до зустрічі з автомобілем?
Розв’язання:
Знайдемо шлях, пройдений автомобілем за 9 с.
Оскільки в першу секунду після досягнення пункту А автомобіль проїхав 30м,
а в кожну наступну секунду він проїжджав на 2 м менше, ніж в попередню, то
відстані, пройдені ним в кожну секунду, складають арифметичну прогресію, перший
член a1
якої рівний 30, а різниця d рівна (-2). Так, як шлях, пройдений автомобілем
за 9-ту секунду, рівний a9 = a1 + d(9
−1)= 30 + (−2)⋅8 =14(м), то шлях,
пройдений автомобілем за 9 с, рівний ![]() a
a![]() + a 30 +14 Тому в той
+ a 30 +14 Тому в той
момент, коли автобус виїхав з пункту В, відстань між ним і автомобілем була рівною 258−198 = 60(м). За першу секунду після виїзду автобуса автомобіль проїде 12 м, а автобус 2 м. Отже, вони зблизяться на 14 м, тобто, їм залишиться проїхати 60−14 = 46(м). За другу секунду вони проїдуть (12− 2)+ (2+1)=13(м), і їм залишиться проїхати 46−13 = 33(м). За четверту секунду вони проїдуть (8− 2)+ (4 +1)=11(м), і їм залишиться проїхати 10 м. За п’яту секунду автомобіль проїде 6− 2 = 4(м), а автобус проїде 5+1= 6(м). Тобто автобус і автомобіль зустрінуться через 5 с після виїзду автобуса із пункту В. За цей час автобус проїде шлях, рівний
2+3+ 4 +5+ 6 = 20(м).
Відповідь: автобус до зустрічі із автомобілем проїхав відстань рівну 20 м. Задача 49.
Згідно розкладу катер проходить рікою, швидкість течії якої км
5 ![]() , шлях
із А в D довжиною 15км за 1 годину. При цьому, год
, шлях
із А в D довжиною 15км за 1 годину. При цьому, год
виходячи з пункту A о 12 годині, він прибуває в пункти B і C, які знаходяться на відстані 11 км і 13 км від A, о 12 годині 20 хвилин і о 12 годині 40 хвилин. Відомо, що якби катер рухався із A в D без зупинок з постійною швидкістю υ (відносно води), то сума абсолютних величин відхилень від розкладу прибуття в пункти B, C, D не перевищувала б зменшеного на півгодини часу, необхідного катеру для проходження 5 км зі швидкістю υ в стоячій воді. Який із пунктів знаходиться вище за течією: A чи D?
Розв’язання:
Припустимо, що пункт D розміщений вище пункту А за течією
річки. Оскільки катер прибув із А в D, рухаючись з швидкістю υкм год відносно води, то повинна виконуватися нерівність υ〉5. Але тоді для
проходження 5 км з швидкістю υкм в стоячій воді катеру год
![]() знадобилося
б менше однієї години. Тому, сума абсолютних величин відхилень від розкладу прибуття
в пункти В, С і D не перевищувала б
знадобилося
б менше однієї години. Тому, сума абсолютних величин відхилень від розкладу прибуття
в пункти В, С і D не перевищувала б ![]() години. Загалом, абсолютна
величина відхилення від розкладу прибуття в пункт D, рівна 15 −1, також не перевищувала
б
години. Загалом, абсолютна
величина відхилення від розкладу прибуття в пункт D, рівна 15 −1, також не перевищувала
б ![]() 1 υ−5 2
1 υ−5 2
години, тобто, була б справедлива нерівність:
15 1 −1 ≤ . υ−5 2
![]() Оскільки
справедлива нерівність a ≤
a, то із нерівності
Оскільки
справедлива нерівність a ≤
a, то із нерівності
![]() 15 1
15 1
![]() −1
≤ випливає нерівність
, звідки υ≥15. Але υ−5 2
−1
≤ випливає нерівність
, звідки υ≥15. Але υ−5 2
якщо швидкість катера в стоячій воді не менша ніж 15 ![]() км , то він год
км , то він год
проходить 5 км в стоячій воді не більше ніж за 20 хвилин, що суперечить умові. Тому, наше міркування про те, що пункт D розміщений вище пункту А за течією річки, суперечить умові задачі.
Отже, пункт D розміщений нижче пункту А за течією річки.
Відповідь: пункт D розміщений нижче пункту А за течією річки. Задача 50.
Два спортсмени стартували один за другим з інтервалом в дві хвилини. Другий спортсмен наздогнав першого на відстані 1 км від точки старту, а пробігши від точки старту 5 км, він повернувся назад і зустрівся з першим спортсменом. Ця зустріч відбулася через 20 хвилин після старту першого спортсмена. Знайдіть швидкість другого спортсмена.
Розв’язання:
Позначимо через
x ![]() км швидкість першого
спортсмена, а через год
км швидкість першого
спортсмена, а через год
км
у ![]() швидкість другого спортсмена.
Перший спортсмен пробіг 1 км год
швидкість другого спортсмена.
Перший спортсмен пробіг 1 км год
за ![]() 1 години, а другий – за
1 години, а другий – за ![]() 1 години. За умовою задачі
другий x y
1 години. За умовою задачі
другий x y
спортсмен затратив на 1 км на 2 хвилини менше часу, ніж перший, отже,
1 1 1
![]() − = .
− = .
x y 30
До моменту зустрічі перший спортсмен, знаходячись
в дорозі 20 хвилин, пробіг ![]() x км. Отже, другий спортсмен до цього
моменту пробіг 10−
x км. Отже, другий спортсмен до цього
моменту пробіг 10− ![]() 1 xкм. Оскільки він
біг 18 хвилин, то
1 xкм. Оскільки він
біг 18 хвилин, то
3
1 18
![]() 10− х = у.
10− х = у.
3 60
Звідки маємо рівняння:
18 х = 10 − ![]() у⋅3.
у⋅3.
60
Яке має корені у1 = 20 і у2 = −50. Оскільки швидкість спортсмена додатна, то у = 20.
Відповідь: швидкість другого спортсмена рівна 20 ![]() км . год
км . год
Задача 51.
Із пункту А в пункт В виїхав велосипедист, а через чверть години вслід за ним виїхав автомобіль. На половині шляху від А до В автомобіль наздогнав велосипедиста. Коли автомобіль прибув в пункт В, велосипедисту залишалося проїхати ще третину шляху. За який час велосипедист проїхав шлях від А до В, якщо відомо, що швидкості велосипедиста і автомобіля постійні на всьому шляху від пункту А до пункту В?
Розв’язання:
Позначимо через х
і у час в хвилинах, який знадобився відповідно велосипедисту і автомобілю
для того, щоб проїхати шлях від пункту А до пункту В. На половину
шляху від А до В велосипедист затратив ![]() x хвилин, а автомобіль
x хвилин, а автомобіль
![]() y хвилин. За умовою
y хвилин. За умовою
2 2
на половині шляху від А до В вони знаходились одночасно, хоча автомобіль виїхав на 15 хвилин пізніше. Отже, справедлива рівність
y x
![]() +15 =
+15 = ![]() .
.
2 2
До моменту прибуття автомобіля в пункт
В велосипедист знаходився в дорозі вже (y +15)
хвилин і проїхав за цей час ![]() відстані від А до В, тобто, затратив
на цей шлях
відстані від А до В, тобто, затратив
на цей шлях ![]() x хвилин. Отже,
x хвилин. Отже,
y +15
= ![]() x.
x.
Отримали систему двох рівнянь ![]() y +15 =
y +15 = ![]() x і y +15 =
x і y +15 = ![]() 2 x з двома
2 x з двома
2 2 3
невідомими х і у. Множачи рівняння ![]() y +15 =
y +15 =
![]() x на 2 і віднімаючи від
x на 2 і віднімаючи від
2 2
нього рівняння y +15
= ![]() x, отримуємо
рівняння 15 = x
−
x, отримуємо
рівняння 15 = x
− ![]() x,
звідки
x,
звідки
x = 45.
Відповідь: велосипедист проїхав шлях від А до В за 45 хвилин.
Задача 52.
Автобус проходить шлях АЕ, який складається із ділянок АВ,
ВС, СD, DE довжиною 10 км, 5 км,
5 км, 6 км відповідно. При цьому, відповідно розкладу, виїжджаючи
із пункту A о 9 годині, він проходить пункт B о 9![]() години, пункт C
– о 9
години, пункт C
– о 9![]() години, пункт D – о 9
години, пункт D – о 9![]() години. З якою постійною швидкістю υ
повинен рухатися автобус, щоб сума абсолютних величин відхилень від розкладу проходження
пунктів B, C, D і часу руху автобуса від A до E
при швидкості υ,
не перевищувала 51,7 хвилини?
години. З якою постійною швидкістю υ
повинен рухатися автобус, щоб сума абсолютних величин відхилень від розкладу проходження
пунктів B, C, D і часу руху автобуса від A до E
при швидкості υ,
не перевищувала 51,7 хвилини?
Розв’язання:
Якщо швидкість автобуса буде υкм , то на шлях із А в Е він год
затратить ![]() годин, а пункти В, C і D він
буде проходити відповідно о 9 +10
годин, а пункти В, C і D він
буде проходити відповідно о 9 +10![]() годин, 9 +15
годин, 9 +15![]() годин і 9 +
годин і 9 + ![]() 20годин. Тобто, сума
20годин. Тобто, сума
υ υ υ
абсолютних величин відхилень від розкладу проходження пунктів В, C, D і часу руху автобуса від А до Е рівна
![]() 10 1 15 3 20 2 26
10 1 15 3 20 2 26
− + − + − + .
υ 5 υ 8 υ 3 υ
В задачі потрібно з’ясувати, при якому значенні υ справедлива нерівність:
10 1 15 3 20 2 26 517
![]() − + − + − + ≤ . υ
5 υ
8 υ
3 υ
600
− + − + − + ≤ . υ
5 υ
8 υ
3 υ
600
Перший спосіб розв’язання нерівності.
Оскільки ![]() −
− ![]() =
= ![]() ,
, ![]() −
− ![]() =
= ![]() (40−υ),
(40−υ),
![]() , то для звільнення від знаків абсолютних величин
, то для звільнення від знаків абсолютних величин
![]() в нерівності 10 − 1 + 15 − 3 + 20 − 2 + 26 ≤ 517 розглянемо чотири
υ
5 υ
8 υ
3 υ
600
в нерівності 10 − 1 + 15 − 3 + 20 − 2 + 26 ≤ 517 розглянемо чотири
υ
5 υ
8 υ
3 υ
600
випадки:
1)0〈υ〈30,
2) 30 ≤υ〈40,
3) 40 ≤υ〈50,
4) 50 ≤υ.
1) Якщо 0〈υ〈30, то нерівність
![]() 10 1 15 3 20 2 26 517
10 1 15 3 20 2 26 517
− + − + − + ≤
υ 5 υ 8 υ 3 υ 600
рівносильна нерівності:
![]() ,
,
звідки ![]() . Оскільки
. Оскільки ![]() , то немає значень υ
з
, то немає значень υ
з
проміжку 0 <υ< 30, які задовольняли б нерівність.
2)Якщо30 ≤υ〈40,то нерівність
10 1 15 3 20 2 26 517
![]() − + − + − + ≤ υ
5 υ
8 υ
3 υ
600
− + − + − + ≤ υ
5 υ
8 υ
3 υ
600
рівносильна нерівності:
![]() ,
,
звідки ![]() . Оскільки
. Оскільки
![]() , то
немає значень υ
із проміжку 30 ≤υ〈40,які задовольняли б нерівність.
, то
немає значень υ
із проміжку 30 ≤υ〈40,які задовольняли б нерівність.
3)Якщо40 ≤υ〈50, то нерівність
10 1 15 3 20 2 26 517
![]() − + − + − + ≤ υ
5 υ
8 υ
3 υ
600
− + − + − + ≤ υ
5 υ
8 υ
3 υ
600
рівносильна нерівності:
![]() ,
,
звідки υ≥ 50. Тобто, немає значень υ із проміжку
40 ≤υ〈50, 40 ≤υ〈50,які задовольняли б нерівність.
4)Якщо υ≥ 50, то нерівність
10 1 15 3 20 2 26 517
![]() − + − + − + ≤ υ
5 υ
8 υ
3 υ
600
− + − + − + ≤ υ
5 υ
8 υ
3 υ
600
рівносильна нерівності:
![]() ,
,
звідки υ≤ 50. Отже, є єдине значення υ= 50, яке задовольняє
![]() нерівність: 10 − 1 + 15 − 3 + 20 − 2 + 26 ≤ 517. υ
5 υ
8 υ
3 υ
600
нерівність: 10 − 1 + 15 − 3 + 20 − 2 + 26 ≤ 517. υ
5 υ
8 υ
3 υ
600
Другий спосіб розв’язання нерівності.
![]() Оскільки
для довільного дійсного числа а справедлива нерівністьа ≤ а, то якщо υ
задовольняє нерівність
Оскільки
для довільного дійсного числа а справедлива нерівністьа ≤ а, то якщо υ
задовольняє нерівність
10 1 15 3 20 2 26 517
![]() −
+ − + − + ≤ , υ 5 υ 8 υ
3 υ
600
−
+ − + − + ≤ , υ 5 υ 8 υ
3 υ
600
то υ задовольняє й нерівність:
![]() ,
,
![]() звідки υ≥ 50. Оскільки − а ≤ а, то υ
задовольняє також і нерівність:
звідки υ≥ 50. Оскільки − а ≤ а, то υ
задовольняє також і нерівність:
![]() ,
,
звідки υ≤ 50. Із нерівностей: υ≥ 50 і υ≤ 50 випливає, що
υ= 50.
Відповідь :автобус має рухатися з постійною швидкістю
50 ![]() км . год
км . год
Задача 53.
Із пункту А в пункт В виїхав
велосипедист. В той момент, коли він проїхав ![]() шляху між А і В,
із В в А виїхав мотоцикліст, який прибув в А, не затримуючись,
повернув назад і одночасно з велосипедистом прибув в В. Час руху мотоцикліста
до першої зустрічі з велосипедистом рівний часу руху мотоцикліста із А в
В. Вважаючи швидкості мотоцикліста при русі із А в В і із В
в А різними, знайдіть, в скільки разів швидкість мотоцикліста при русі із
А в В більша швидкості велосипедиста.
шляху між А і В,
із В в А виїхав мотоцикліст, який прибув в А, не затримуючись,
повернув назад і одночасно з велосипедистом прибув в В. Час руху мотоцикліста
до першої зустрічі з велосипедистом рівний часу руху мотоцикліста із А в
В. Вважаючи швидкості мотоцикліста при русі із А в В і із В
в А різними, знайдіть, в скільки разів швидкість мотоцикліста при русі із
А в В більша швидкості велосипедиста.
Розв’язання:
Позначимо через S км відстань між пунктами А
і В, через U ![]() км год
км год
швидкість мотоцикліста на шляху із В в А, через υкм швидкість год
велосипедиста, через х шукане відношення швидкості мотоцикліста на шляху із А в В до швидкості велосипедиста. Тоді швидкість
мотоцикліста на шляху із А в В рівна хυкм . год
На рух із пункту А в пункт В мотоцикліст витратив
![]() S годин. За xυ
S годин. За xυ
умовою задачі такий же час пройшов між моментом виїзду мотоцикліста із пункту В і моментом першої зустрічі з велосипедистом. За цей час велосипедист проїхав S υ км, а xυ
мотоцикліст ![]() S U км. Оскільки в момент
виїзду мотоцикліста із xυ
S U км. Оскільки в момент
виїзду мотоцикліста із xυ
пункту В відстань між ним і велосипедистом рівна ![]() Sкм,
то справедлива рівність: S υ+
Sкм,
то справедлива рівність: S υ+
![]() S U =
S U =
![]() 3 S, чи, оскільки
υ〉0,S〉0,
3 S, чи, оскільки
υ〉0,S〉0,
xυ xυ 4
рівність:
1 U 3
![]() + = . x υx
4
+ = . x υx
4
![]() Мотоцикліст
знаходився в дорозі S + S годин. За цей час
Мотоцикліст
знаходився в дорозі S + S годин. За цей час
U xυ
![]() велосипедист
проїхав
велосипедист
проїхав ![]() 3 S км. Тому
S + S υ=
3 S км. Тому
S + S υ= ![]() 3 S чи
3 S чи
4 U xυ 4 υ 1 3
![]() + = .
+ = .
U x 4
Із цього рівняння отримуємо:
U 4x
![]() = .
υ
3x − 4
= .
υ
3x − 4
![]() Підставляючи
Підставляючи
![]() 4х замість U
4х замість U![]() в рівняння
1 + U = 3, маємо
в рівняння
1 + U = 3, маємо
3х − 4 υ x υx 4
рівняння:
1 4 3
![]() + = .
+ = .
x 3x − 4 4
Це рівняння має корені
x1 = 4 і x2 = ![]() . Із умови задачі зрозуміло,
що швидкість мотоцикліст на шляху із А в В більша швидкості велосипедиста,
тобто, х〉1.
Значить, х = 4.
. Із умови задачі зрозуміло,
що швидкість мотоцикліст на шляху із А в В більша швидкості велосипедиста,
тобто, х〉1.
Значить, х = 4.
Відповідь: швидкість мотоцикліста при русі із А в В в 4 рази більша швидкості велосипедиста. Задача 54.
Пішохід, велосипедист і мотоцикліст рухаються по шосе в одну сторону з постійними швидкостями. В той момент, коли пішохід і велосипедист знаходились в одній точці, мотоцикліст був на відстані 6 км позаду них. В той момент, коли мотоцикліст наздогнав велосипедиста, пішохід відставав від них на 3 км. На скільки кілометрів велосипедист обігнав пішохода в той момент, коли пішохода наздогнав мотоцикліст?
Розв’язання:
Перше розв’язання.
Позначимо через υм ![]() км швидкість мотоцикліста,
через υв
км швидкість мотоцикліста,
через υв ![]() км год год
км год год
швидкість велосипедиста,
через υп ![]() км — швидкість пішохода.
Нехай год
км — швидкість пішохода.
Нехай год
з моменту зустрічі пішохода і велосипедиста до зустрічі мотоцикліста і пішохода пройшло t1 години, а з моменту зустрічі пішохода і велосипедиста до зустрічі мотоцикліста і велосипедиста пройшло t2 години. За час t1 мотоцикліст проїхав υмt1км,а пішохід пройшов υпt1км. Із умови задачі маємо рівняння:
υмt1 −υпt1 = 6.
З моменту зустрічі мотоцикліста і пішохода до зустрічі мотоцикліста і велосипедиста пройшло (t2 −t1 ) години. За цей час мотоцикліст проїхав υм (t2 −t1 )км, а пішохід пройшов υп (t2 −t1 )км, і оскільки як пішохід відстав на 3 км, то маємо ще одне рівняння: υм (t2 −t1 )−υп (t2 −t1 )= 3.
Із умови, що велосипедист обігнав пішохода на 3 км, отримаємо рівняння:
υвt2 −υпt2 = 3. Тому отримали систему рівнянь:
υмt1 −υпt1 = 6,
υм(t2 −t1 )−υп (t2 −t1 )= 3,
υвt2 −υпt2 = 3.
Потрібно знайти, на скільки кілометрів велосипедист обігнав пішохода в той момент, коли пішохода наздогнав мотоцикліст. Оскільки як це відбулося через t1 годин, то за цей час велосипедист проїхав υвt1км, а пішохід пройшов υпt1км.
Тобто, шукана відстань х рівна (υвt1 −υпt1 )км. Із першого рівняння системи: (υм −υп )t1 = 6, із другого рівняння системи:
(υм −υп )(t2 −t1 )= 3, звідки ![]() t1 = 2, тобто, t2 =
t1 = 2, тобто, t2 = ![]() 3t1. Із останнього
3t1. Із останнього
t2 −t1 2
рівняння системи: υв −υп =
![]() 3 , тому
3 , тому
t2
x 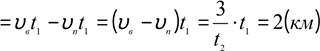 .
.
Друге розв’язання.
Позначимо через υм ![]() км швидкість мотоцикліста,
через υв
км швидкість мотоцикліста,
через υв ![]() км год год
км год год
швидкість велосипедиста, через υп ![]() км швидкість пішохода.
Час, за год
км швидкість пішохода.
Час, за год
який велосипедист обігнав пішохода на 3км, рівний 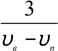 . Із умови
. Із умови
задачі випливає,
що цей же час рівний 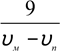 , звідки
, звідки
3 9 υв −υп 1
![]()
![]() = , чи = . Мотоцикліст наздогнав
пішохода за
= , чи = . Мотоцикліст наздогнав
пішохода за
υв −υп υм −υп υм −υп 3
час 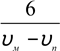 . Тобто, за цей час велосипедист обігнав пішохода
на:
. Тобто, за цей час велосипедист обігнав пішохода
на:
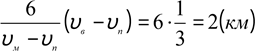 .
.
Відповідь: велосипедист обігнав пішохода в той момент, коли пішохода наздогнав мотоцикліст, на 2 км.
Задача 55.
Із пункту А в пункт В вийшов пішохід, і одночасно із пункту В в пункт А виїхав мотоцикліст. Зустрівши в дорозі пішохода, мотоцикліст одразу ж розвернувся, довіз пішохода до пункту В, а потім одразу ж знову поїхав в пункт А, куди дістався без перешкод. В результаті цього мотоцикліст затратив на дорогу до пункту А в два з половиною рази більше часу, ніж якби він їхав із пункту В в пункт А, не підвозячи пішохода. В скільки разів повільніше пішохід дістався б до пункту В, якби весь шлях від А до В він пройшов пішки?
Розв’язання:
Позначимо через υп ![]() км і υм
км і υм ![]() км відповідно швидкості
пішохода
км відповідно швидкості
пішохода
год год
і мотоцикліста, а через t годин — час, через який вони зустрілись.
За час t пішохід пройшов υп ⋅t км, а мотоцикліст проїхав υмt км.
![]() Якби мотоцикліст не підвозив пішохода, то на шлях від В
до А він витратив би υп ⋅t +υм ⋅t годин. Оскільки мотоцикліст
підвозив υм
Якби мотоцикліст не підвозив пішохода, то на шлях від В
до А він витратив би υп ⋅t +υм ⋅t годин. Оскільки мотоцикліст
підвозив υм
![]()
![]() υп ⋅t
годин. Із умови пішохода, то він прибув в пункт А через 3t
+
υм
υп ⋅t
годин. Із умови пішохода, то він прибув в пункт А через 3t
+
υм
![]() задачі відомо, що на це він затратив в разу більше часу, ніж
у випадку, коли б він не підвозив пішохода, тому: υп ⋅t 3t +
задачі відомо, що на це він затратив в разу більше часу, ніж
у випадку, коли б він не підвозив пішохода, тому: υп ⋅t 3t +
υм 5
![]() = .
= .
![]() Якби весь
шлях від А до В пішохід пройшов пішки, то він затратив би на весь
шлях t +υυмпt годин, а в дійсності він
затратив на
Якби весь
шлях від А до В пішохід пройшов пішки, то він затратив би на весь
шлях t +υυмпt годин, а в дійсності він
затратив на
весь шлях 2t годин. В задачі потрібно знайти, в скільки разів час
υмt
t +
![]()
![]() t +υмt
більший часу 2t , тобто, потрібно знайти величину υп ,
t +υмt
більший часу 2t , тобто, потрібно знайти величину υп ,
υп 2t
![]()
![]() υп ⋅t
υп ⋅t
1+ 3t + ![]()
![]() чи величину
чи величину ![]() . Із маємо:
3υм +υп = 5, звідки
. Із маємо:
3υм +υп = 5, звідки
2υп +υм 2
![]()
![]() 6υм + 2υп = 5υп +5υм чи υм = 3υп , тобто, мп = 3. Отже, 1+υмп :2
= 2,
6υм + 2υп = 5υп +5υм чи υм = 3υп , тобто, мп = 3. Отже, 1+υмп :2
= 2,
υ
тобто, якби мотоцикліст не підвозив пішохода, то пішохід дістався б до А в два рази повільніше.
Відповідь: пішохід дістався б до пункту В в 2 рази повільніше, якби весь шлях від А до В він пройшов пішки. Задача 56.
Два тіла рухаються рівномірно назустріч одне одному і відстань між ними зменшується на S1 =16м за кожні t1 =10c. Якщо ці тіла з такими самими швидкостями рухатимуться в одному напрямі, то відстань між ними збільшуватиметься на S2 = 3м за кожні t2 = 5c. З якою швидкістю рухається кожне з цих тіл?
υ υ
Розв’язання:
Систему координат зв’яжемо з першим тілом і
вісь OS спрямуємо в напрямі швидкості υ1 першого тіла. У цій системі
відліку перше тіло перебуває в спокої, а друге рухається відносно першого з швидкістю
υ1 +υ2 у першому випадку і з швидкістю
υ1 −υ2 в другому. Тоді S1 = (υ1 +υ2 )⋅t1 і S2 = (υ1 −υ2 )t2 , або υ1 +υ2 =
![]() S1 і t1
S1 і t1
|
S υ1 −υ2 = t2 |
|
|
|
t1 t2 t1 t2 м υ1 =1,1 |
останніх |
рівнянь, |
Відповідь: перше тіло рухається зі швидкістю 1,1 ![]() м, друге тіло с
м, друге тіло с
рухається
зі швидкістю 0,5 ![]() м. с
м. с
Задача 57.
![]() Автомобілі А і В з однаковою
Автомобілі А і В з однаковою
швидкістю υ1 =υ2 = 20 ![]() м рухаються с
м рухаються с
по двох шосе, які перетинаються в точці О під кутом α= 60°. Визначити мінімальну відстань між автомобілями, якщо в певний момент вони знаходилися на відстанях d1 = 30км і d2 = 60км від перехрестя доріг.
Розв’язання:
Задачі такого типу зручно розв’язувати в системі відліку, зв’язаній з одним із рухомих тіл. Припустимо, що систему відліку ми зв’язали з автомобілем В, тобто в цій системі автомобіль В нерухомий, а автомобіль А рухається відносно В. Знайдемо відносну швидкість автомобіля А. Для цього з кінця вектора швидкості υ1 відкладемо вектор −υ2 ,тоді відносна швидкість автомобіля А буде
![]()
υв =υ1 −υ2 . Отже, спостерігач, який сидить в автомобілі В, вважає, що автомобіль А рухається по лінії АС. Щоб знайти мінімальну відстань між автомобілями, опустимо з точки В на продовження лінії
АС перпендикуляр BD, який і буде мінімальною відстанню
BD = (OB −OA)sin60° = (d2 − d1 )sin60° ≈ 25,6(км).
Відповідь: мінімальна відстань між автомобілями рівна ≈ 25,6км.
Задача 58.
Два автобуси одночасно виїхали з пункту А в пункт В. Один з них першу половину шляху їхав зі сталою швидкістю υ1 , а решту шляху — зі швидкістю υ2. Другий автобус їхав зі швидкістю υ1 половину всього часу свого руху від А до В, а решту часу — зі швидкістю υ2. Визначити середню швидкість руху кожного автобуса,
якщо υ1 = 30 ![]() км і υ2 = 50
км і υ2 = 50 ![]() км . год год
км . год год
Розв’язання:
Досить часто при розв’язуванні
цієї задачі учні помилково вважають, що середня швидкість обох автобусів буде υс =![]() .
.
Проте так можна визначити середню швидкість тільки тоді, коли автобус рухається однакові проміжки часу з кожною із швидкостей, тобто середню швидкість другого автобуса. Середнє значення швидкості визначається у відношенні до часу, а не у відношенні до пройденого шляху. Тому:
υ1 1t +υ2t2 S1 + S2
![]() υс = = , t1 +t2 t1 +t2
υс = = , t1 +t2 t1 +t2
або
S
υc = ![]() ,
,
t
де S —повна відстань, а t—час, за який цю відстань проходить
автобус.
![]() Для першого автобуса:
S = 0,5S
+ 0,5S
і t = t1 +t2 = 0,5S + 0,5S .
Для першого автобуса:
S = 0,5S
+ 0,5S
і t = t1 +t2 = 0,5S + 0,5S .
υ1 υ2
Тоді
S 2υ1υ2 км
υс1 = = =
37,5 ![]() .
.
![]() 1 1 υ1 +υ2 год
1 1 υ1 +υ2 год
0,5Sυ1 +υ2
S 2υ1υ2 км
υc1 = = ≈
37,5 ![]() .
.
![]() 1 1 υ1 +υ2 год
1 1 υ1 +υ2 год
0,5Sυ1 +υ2
Для другого автобуса: t = 0,5t + 0,5t і S = 0,5υ1t + 0,5υ2t = 0,5t(υ1 +υ2 ).
тоді
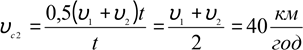 .
.
Відповідь: середня швидкість першого автобуса рівна 37,5 ![]() км , год
км , год
середня швидкість
другого автобуса рівна 40 ![]() км . год
км . год
Задача 59.
Два тіла почали одночасно рухатися в одному напрямі: одне
рівномірно з швидкістю
υ1 = 54 ![]() км , а друге з прискоренням
год
км , а друге з прискоренням
год
м а = 0,6 ![]() 2 . Через скільки часу друге
тіло наздожене перше?
2 . Через скільки часу друге
тіло наздожене перше?
с
Розв’язання:
За початок системи координат візьмемо точку, з якої почали рухатися обидва тіла, а вісь OS спрямуємо в напрямі руху обох тіл.
Через час t від початку руху координати тіл будуть S1 =υ1t і S2 =
![]() at 2 . 2 Якщо друге тіло наздогнало
перше, то координати тіл будуть
at 2 . 2 Якщо друге тіло наздогнало
перше, то координати тіл будуть
однаковими, тобто S1 =
S2 ,або
υ1t = ![]() at 2 , звідки t =
at 2 , звідки t = ![]() 2υ1 = 50c.
2υ1 = 50c.
2 a
Відповідь: друге тіло наздожене перше через 50 с.
Задача 60.
Одне тіло кидають вертикально вгору з висоти H з початковою швидкістю υ1. Одночасно з початком руху першого тіла з землі кидають угору друге тіло з початковою швидкістю υ2. Через який час тіла зустрінуться?
Розв’язання:
За початок системи координат візьмемо точку
кидання першого тіла і вісь координат OS спрямуємо вертикально вгору. Тоді
в момент часу t координата першого тіла буде S1 =υ1t − ![]() gt 2 і, отже, через час t
його відстань від землі буде H +
S1 = H +υ1t −
gt 2 і, отже, через час t
його відстань від землі буде H +
S1 = H +υ1t − ![]() gt 2. Через час t від
початку руху друге тіло буде від землі на відстані
gt 2. Через час t від
початку руху друге тіло буде від землі на відстані
S2 =υ2t − ![]() gt 2.
gt 2.
Якщо t дорівнює
тому проміжку часу, через який тіла зустрінуться, то H + S1 = S2 , або H +υ1t − ![]() gt 2 =υ2t −
gt 2 =υ2t − ![]() gt 2 , звідки:
gt 2 , звідки:
H
t = ![]() . υ2 −υ1 Відповідь: тіла зустрінуться через t
=
. υ2 −υ1 Відповідь: тіла зустрінуться через t
= ![]() H .
υ2 −υ1
H .
υ2 −υ1
Задача 61.
Пасажир потягу, що рухається зі швидкістю υ1 = 36 ![]() км , бачить год
км , бачить год
протягом t1 = 60cсусідній потяг довжиною l = 600м, який іде паралельно першому в одному з ним напрямі. З якою швидкістю йде другий потяг? Скільки часу пасажир другого потягу бачить перший потяг, довжина якого l1 = 900м?
Ті самі потяги рухаються назустріч один одному. Скільки часу пасажири цих поїздів бачитимуть зустрічний потяг, що рухається повз них?
Розв’язання: Систему відліку пов’яжемо з першим потягом.
а) Коли потяги рухаються в одному напрямі, то швидкість другого потяга відносно першого υв =υ2 −υ1. З другого боку, відносна
![]() швидкість υ2 = l2 = l1 =10
швидкість υ2 = l2 = l1 =10 ![]() м. Тоді υ2 =υв +υ1 = 20
м. Тоді υ2 =υв +υ1 = 20 ![]() м = 72
м = 72 ![]() км , а час t2 , t1 t2 с с год
км , а час t2 , t1 t2 с с год
протягом якого пасажир
другого потягу бачить перед собою перший потяг, t2 = ![]() l1 = 90с.
l1 = 90с.
υв
б) Якщо потяги рухаються один одному назустріч, то відносна швидкість υв =υ1 +υ2 , а час, протягом якого кожен пасажир бачитиме зустрічний потяг:
l2 l1 t1 = ![]() = 20c і t2 =
= 20c і t2 = ![]() = 30c. υ1 +υ2 υ1 +υ2
= 30c. υ1 +υ2 υ1 +υ2
Відповідь:
другий потяг йде зі швидкістю 72 ![]() км , а час протягом год
км , а час протягом год
якого пасажир другого потягу бачить перед собою перший потяг, 90с; пасажири бачитимуть зустрічний потяг, що рухається повз них, 20 с і 30 с відповідно.
Задача 62.
Теплохід А, довжина якого l1 = 65м, в стоячій воді розвиває швидкість υ1, а теплохід В, довжина якого l2 = 40м, розвиває швидкість υ2 (υ1〉υ2 ). Теплоходи пливуть за течією річки, і теплохід А обганяє теплохід В за t1 = 70c. Якщо теплохід А пливе за течією, а В— проти течії, то теплоходи минають один одного за t2 =14c. Визначити швидкість теплоходів у стоячій воді.
Розв’язання:
У системі відліку, пов’язаній з другим теплоходом, рівняння руху першого теплохода запишемо:
(υ1 −υ2 )t1 = l1 −l2 і (υ1 +υ2 )t2 = l1 +l2. Розв’язавши ці рівняння, дістанемо:
υ1 = (l1 +l2 )(t1 +t2 ) = 4,5 ![]() м і υ2 = (l1 +l2 )(t1 −t2 ) = 3
м і υ2 = (l1 +l2 )(t1 −t2 ) = 3 ![]() м.
м.
2t t1 2 с 2t t1 2 c
Відповідь: швидкість теплоходу А в стоячій воді становить
4,5 ![]() м,
швидкість теплоходу В в стоячій воді становить 3
м,
швидкість теплоходу В в стоячій воді становить 3 ![]() м. с с
м. с с
Задача 63.
Відстань між двома стоянками моторний човен проходить за течією річки за 10 хв, а проти течії—за 30 хв. За який час цю відстань пропливе за течією рятувальний круг, що впав у воду?
Розв’язання:
У системі відліку, пов’язаній з берегом, рівняння руху човна за течією і проти течії запишемо S = (υ+υ0 )t1 і S = (υ−υ0 )t2 , а рівняння руху рятувального круга— S =υ0t3 , де S —відстань між станціями.
Вилучивши з цих трьох рівнянь величини S, υ і υ0 , дістанемо:
2t t1 2
t3
= ![]() = 30хв. t2 −t1
= 30хв. t2 −t1
Відповідь: рятувальний круг, що впав у воду, пропливе за течією цю відстань за 30 хв. Задача 64.
Між двома пунктами, розташованими на річці на відстані l =100км один від одного, курсує катер. Катер проходить цю відстань за течією за t1 = 4год, а проти течії за t2 =10год. Визначити швидкість течії річки υ1 і швидкість катера υ2 відносно води.
Розв’язання:
Для руху катера вгору і вниз по річці можна записати рівняння:
l = (υ1 +υ2 )t1 і l = (υ2 −υ1 )t2. Розв’язавши цю систему рівнянь відносно υ1 і υ2 , дістанемо:
t2 −t1 км
υ1 = l ![]() = 7,5
= 7,5![]()
2t t1 2 год
t1 +t2 км
υ2 = l ![]() =17,5
=17,5 ![]() .
.
2t t1 2 год
Відповідь: швидкість течії річки
становить 7,5 ![]() км , а швидкість год
км , а швидкість год
катера відносно
води становить17,5 ![]() км . год
км . год
Задача 65.
Відстань між кінцевими
зупинками тролейбуса 6 км. Через кожні 5 хв з кінцевої зупинки відходить
тролейбус і рухається із середньою швидкістю 18 ![]() км . Скільки тролейбусів
зустріне на год
км . Скільки тролейбусів
зустріне на год
протязі всього маршруту пасажир, що знаходиться в зустрічному тролейбусі, який рухається з такою самою середньою швидкістю? Розв’язання:
![]()
Побудуємо графіки шляхів зустрічних тролейбусів і тролейбуса, в якому їде пасажир. З малюнка видно, що пасажир зустріне 7 тролейбусів.
Відповідь: на протязі свого маршруту пасажир, що знаходиться в зустрічному тролейбусі, зустріне 7 тролейбусів.
Задача 66.
Літак летить по прямій з міста А в місто В і повертається назад. Визначити відношення повних часів польоту у випадках, коли від А до В дме вітер з швидкістю u і коли вітер з тією самою швидкістю дме перпендикулярно до лінії А—В. Швидкість літака відносно повітря в обох випадках однакова і дорівнює υ.
Розв’язання:
Коли вітер дме від А до В, то повний час польоту:
S S
![]() t1 = + . υ+u υ−u
t1 = + . υ+u υ−u
![]()
![]() Якщо ж вітер дме перпендикулярно до
напряму польоту, то швидкість літака відносно повітря υ повинна
бути спрямована під таким кутом до прямої АВ, щоб швидкість літака відносно
землі υв = υ2 −u 2 була спрямована вздовж
прямої АВ. Повний час польоту в цьому випадку t2 =
2S 2 , а відношення часів польоту:
υ2 −u
Якщо ж вітер дме перпендикулярно до
напряму польоту, то швидкість літака відносно повітря υ повинна
бути спрямована під таким кутом до прямої АВ, щоб швидкість літака відносно
землі υв = υ2 −u 2 була спрямована вздовж
прямої АВ. Повний час польоту в цьому випадку t2 =
2S 2 , а відношення часів польоту:
υ2 −u
t2 1 2 2
![]() =
υ
−u .
=
υ
−u .
t1 υ
Відповідь: повний час польоту у випадках, коли від А до В дме
![]() вітер зі швидкістю u :t1 =
S +
S
і коли вітер з тією самою υ+u υ−u
вітер зі швидкістю u :t1 =
S +
S
і коли вітер з тією самою υ+u υ−u
![]() швидкістю дме перпендикулярно до лінії
А—В: t2
= 2S 2 , а υ2 −u
швидкістю дме перпендикулярно до лінії
А—В: t2
= 2S 2 , а υ2 −u
![]() відношення
часів польоту: t2 = 1 υ2 −u 2 .
відношення
часів польоту: t2 = 1 υ2 −u 2 .
t1 υ
Задача 67.
Під час польоту літака з пункту А в пункт В і назад дув вітер у
напрямі з пункту
А в пункт В зі швидкістю υ0 =16 ![]() м. У скільки разів с
м. У скільки разів с
довше тривав цей політ порівняно з польотом з пункту А в пункт В і назад у безвітряну погоду? Швидкість літака у безвітряну погоду
км υ=180 ![]() .
.
год
Розв’язання:
![]() Повний час польоту під час вітру t1 =
S +
S ,а
в υ+υ0 υ−υ0
Повний час польоту під час вітру t1 =
S +
S ,а
в υ+υ0 υ−υ0
![]() 2S t1 υ2 безвітряну погоду t2 =
2S t1 υ2 безвітряну погоду t2 = ![]() . Тоді
= ≈1,11.
υ t
. Тоді
= ≈1,11.
υ t![]()
Відповідь: політ тривав довше приблизно в 1,11 раз порівняно з польотом з пункту А в пункт В і назад у безвітряну погоду. Задача 68.
Човен рухається вниз за течією річки по прямій, напрямленій під кутом α= 30° до берега. Визначити мінімальне значення швидкості
човна відносно води, якщо швидкість течії річки υ= 2,5 ![]() м. с Розв’язання:
м. с Розв’язання:
Швидкість човна відносно води буде мінімальною тоді, коли ця швидкість буде спрямована перпендикулярно до течії річки. Отже,
м
υм =υtgα≈1,44 ![]() .
.
с
Відповідь: мінімальне значення швидкості човна відносно води
становить
≈1,44 ![]() м. с Задача
69.
м. с Задача
69.
Два рибалки переправляються на човнах через річку, ширина якої d = 280м,тримаючи курс перпендикулярно до берега. Швидкість
течії річки u =1![]() м. Зусиллями рибалок
човнам надаються швидкості с
м. Зусиллями рибалок
човнам надаються швидкості с
υ1 =1,4
![]() м
і υ2 =1,6
м
і υ2 =1,6 ![]() м. На якій відстані один
від одного пристануть с с човни до берега, якщо вони виїхали з одного
пункту? Розв’язання: Перший рибалка перепливе річку за час t1 =
м. На якій відстані один
від одного пристануть с с човни до берега, якщо вони виїхали з одного
пункту? Розв’язання: Перший рибалка перепливе річку за час t1 =
![]() d і буде знесений υ1
d і буде знесений υ1
течією відносно берега на відстань l1 =
![]() d u, а другий рибалка
υ1
d u, а другий рибалка
υ1
затратить час t2 =
![]() d і буде знесений течією
на відстань l2 =
d і буде знесений течією
на відстань l2 =
![]() d u. υ2 υ2
d u. υ2 υ2
Відстань між точками, в яких пристануть човни:
du(υ2 −υ1 )
х = l1 −l2 = ![]() = 25(м).
= 25(м).
υ1υ2 Відповідь: човни пристануть до берега на відстані 25 м один від одного. Задача 70.
Човен перепливає річку під кутом α= 30° до берега вниз за
течією. Швидкість човна відносно води
υ1 =1,5 ![]() м, швидкість течії с
м, швидкість течії с
річки υ2 = 2 ![]() м. Визначити швидкість
човна відносно берега. с
м. Визначити швидкість
човна відносно берега. с
Розв’язання:
Легко
переконатися, що швидкість човна υ1 не може бути спрямована
перпендикулярно до течії річки, тому що ![]() . Згідно
. Згідно
з теоремою
косинусів: ![]() 0, звідки
0, звідки
![]() 2 1 2 м м υx =υ2 cos30°± υ1 − υ2 ; а υx1 ≈ 2,84
2 1 2 м м υx =υ2 cos30°± υ1 − υ2 ; а υx1 ≈ 2,84 ![]() і υх2 ≈ 0,62
і υх2 ≈ 0,62 ![]() .
.
4 с с
Відповідь: швидкість човна відносно берега становить 2,84
![]() м, а с
м, а с
також швидкість
човна може становити й 0,62 ![]() м. с
м. с
Задача 71.
Спортсмен перепливає річку шириною d . Під яким кутом α до течії він повинен пливти, щоб потрапити на протилежний берег за найкоротший час? Де він у цьому випадку пристане до берега і яку відстань S пропливе, якщо швидкість течії υ1, а швидкість спортсмена відносно води υ2.
Розв’язання:
Час руху буде мінімальним, якщо швидкість спортсмена
відносно води υ2 буде спрямована перпендикулярно
до течії. Цей час дорівнює t = ![]() d . За цей час течія
знесе спортсмена на відстань
d . За цей час течія
знесе спортсмена на відстань
υ2
![]()
![]() S1 =υ1t =
S1 =υ1t =![]() d. Швидкість
спортсмена відносно берега υ= υ12 +υ22. За час t спортсмен
пропливе S =υt
=
d υ12 +υ22. υ2
d. Швидкість
спортсмена відносно берега υ= υ12 +υ22. За час t спортсмен
пропливе S =υt
=
d υ12 +υ22. υ2
![]() Відповідь:
спортсмен, щоб потрапити на протилежний берег за найкоротший час повинен пливти
перпендикулярно до течії; спортсмен пропливе таку відстань S =υt
=
d υ12 +υ22. υ2
Відповідь:
спортсмен, щоб потрапити на протилежний берег за найкоротший час повинен пливти
перпендикулярно до течії; спортсмен пропливе таку відстань S =υt
=
d υ12 +υ22. υ2
Задача 72.
На відстані l = 200м мисливська собака помітила зайця. Через
який час вона наздожене його, якщо швидкість зайця υ1 = 40 ![]() км , а год
км , а год
собаки υ2 = 60 ![]() км ? год
км ? год
Розв’язання:
Систему відліку пов’яжемо з Землею і спрямуємо
вісь OX в напрямі бігу зайця й собаки. У цій системі рівняння руху запишемо
так: x3 = l +υ1t і xc =υ2t. У той момент,
коли собака наздогнав зайця, їхні координати будуть однаковими, тобто xз = хс або l +υ1t =υ2t, звідки t = ![]() l = 36c. (Задачу можна
розв’язувати і в системі υ2 −υ1
l = 36c. (Задачу можна
розв’язувати і в системі υ2 −υ1
відліку, пов’язаній з зайцем або собакою.) Відповідь: собака наздожене зайця через 36 с.
Задача 73.
Людина знаходиться на відстані h = 50м від дороги, по якій
наближається
автобус зі швидкістю υ1 =10
![]() м. с
м. с
а)В якому напрямі повинна бігти людина, щоб зустрітися з автобусом, якщо автобус знаходиться на відстані l = 200м від
людини і якщо
людина може бігти зі швидкістю υ2 =
3 ![]() м ? с
м ? с
б)З якою найменшою швидкістю повинна бігти людина, щоб
зустрітися з автобусом?
Розв’язання:
![]() Автобус знаходиться в точці А, а людина в точці В.
Нехай людина зустрічається з автобусом у точці С. Позначимо
через α
кут між напрямом, по якому видно автобус, і напрямом, по якому
Автобус знаходиться в точці А, а людина в точці В.
Нехай людина зустрічається з автобусом у точці С. Позначимо
через α
кут між напрямом, по якому видно автобус, і напрямом, по якому
повинна бігти людина. Нехай людина прибіжить у точку С через t2 , а автобус прийде в цю саму точку через t1, тоді AC =υ1 1t і BC =υ2t2.
З трикутника АВС видно, що AC
=
![]() lsinα,
де sinβ=
lsinα,
де sinβ=
![]() h . Отже, sinβ BC
h . Отже, sinβ BC
![]() sinα= h ⋅υ1 1t . За умовою задачі
t1〉t2 , тому sinα≥
sinα= h ⋅υ1 1t . За умовою задачі
t1〉t2 , тому sinα≥ ![]() hυ1 ≈ 0,8333. Звідси l υ2t2 lυ2
hυ1 ≈ 0,8333. Звідси l υ2t2 lυ2
56°24′ ≤α≤123°36′.
Отже, напрями, по яких може бігти людина, лежать у межах кута DBE. Під час бігу вздовж BD чи BE людина досягне шосе одночасно з автобусом. В будь-яку з точок шосе, які містяться між точками D і E, людина прибіжить раніше від автобуса. Найменшу швидкість, з якою повинна бігти людина, щоб зустріти автобус,
можна визначити з умов: t1 = t2 і sinα=
![]() hυ1 =1. Звідси
hυ1 =1. Звідси
lυ2
h м υ2 = υ1 = 2,5 ![]() . l c
. l c
Відповідь: напрями, по яких може бігти людина лежать в межах кута DBE; найменша швидкість, з якою повинна бігти людина, щоб
зустріти автобус,
рівна 2,5 ![]() м. с
м. с
Задача 74.
Автомобіль проїхав відстань від А до В зі швидкістю
υ1 = 60 ![]() км , год
км , год
а назад повертався
зі швидкістю υ2 = 20 ![]() км . Яка середня швидкість
год
км . Яка середня швидкість
год
руху автомобіля?
Розв’язання:
Середня швидкість руху автомобіля:
2S 2υ1υ2 км
![]() υс = = = 30
υс = = = 30 ![]() . t1 +t2 υ1 +υ2 год
. t1 +t2 υ1 +υ2 год
Відповідь: середня швидкість руху автомобіля рівна 30
![]() км . год
км . год
Задача 75.
На дистанції S =1500м одночасно стартують два бігуни. Бігун А
пробіг першу половину шляху з швидкістю
υ1 = 4 ![]() м, а другу—з с
м, а другу—з с
швидкістю υ2 = 6 ![]() м. Бігун В пробіг
першу половину часу, с
м. Бігун В пробіг
першу половину часу, с
затраченого на подолання всієї дистанції, з швидкістю υ1 = 4 ![]() м, а с
м, а с
другу—з швидкістю
υ2 = 6 ![]() м. Який з бігунів фінішує
першим? На яку с
м. Який з бігунів фінішує
першим? На яку с
відстань він обжене другого бігуна?
Розв’язання: Середня швидкість бігуна А: υс1 =
![]() 2υ1υ2 = 4,8
2υ1υ2 = 4,8 ![]() м, а бігуна В:
м, а бігуна В:
υ1 +υ2 с
υ1 +υ2 м
![]() υс2 = = 5 . Оскільки
середня швидкість бігуна В більша, то він
υс2 = = 5 . Оскільки
середня швидкість бігуна В більша, то він
2 с
фінішує першим, затративши час t2 =
![]() S . За цей час бігун
А
S . За цей час бігун
А
υc2
пробіжить відстань S1 =υc1 ![]() S . Отже, бігун В
обжене бігуна А на
S . Отже, бігун В
обжене бігуна А на
υc2 υc1 відстань ∆S = S − S1 = S − S ![]() = 60м.
= 60м.
υc2
Відповідь: фінішує першим бігун В, який обжене бігуна А на 60 м. Задача 76.
Знайти середню швидкість потяга, коли відомо, що першу
третину шляху він пройшов з швидкістю υ1 = 50 ![]() км , другу— год
км , другу— год
км
υ2 = 75 ![]() , а останню—з
швидкістю, вдвічі більшою за середню год
, а останню—з
швидкістю, вдвічі більшою за середню год
швидкість на перших двох ділянках.
Розв’язання:
Середня швидкість
потяга: υс = ![]() S , де t1 =
S , де t1 = ![]() S , t2 =
S , t2 = ![]() S . t1 +t2 +t3 3υ1 3υ2
S . t1 +t2 +t3 3υ1 3υ2
Щоб знайти t3 , обчислимо спочатку середню швидкість потяга на
S
![]() перших двох третинах
шляху:υc′ = =
2υ1υ2 . Тоді швидкість
перших двох третинах
шляху:υc′ = =
2υ1υ2 . Тоді швидкість
1 S + 1 S υ1 +υ2 3υ1 3υ2
![]() 1
1 ![]() S(υ1 +υ2 )
S(υ1 +υ2 )
поїзда на останній третині шляху υ3 = ,
а t3 = ![]() .
.
Підставивши значення t1, t2 і t3 у формулу для υc , дістанемо:
12υ1υ2 км
![]() υс = = 72
υс = = 72 ![]() .
.
5(υ1 +υ2 ) год
Відповідь: середня швидкість потягу рівна 72 ![]() км . год Задача
77.
км . год Задача
77.
Велосипедист їхав з одного міста до другого. Половину шляху
він проїхав з швидкістю υ1 =12 ![]() км . Далі половину часу
руху, що год
км . Далі половину часу
руху, що год
залишився, він їхав з швидкістю υ2 = 6 ![]() км , а потім до кінця
шляху год
км , а потім до кінця
шляху год
йшов пішки з швидкістю
υ3 = 4 ![]() км . Визначити середню
швидкість год
км . Визначити середню
швидкість год
руху велосипедиста на всьому шляху.
Розв’язання: Середня швидкість велосипедиста:
S1 + S2 + S3
υс = ![]() ,
,
t1 +t2 +t3
де S1,S2 і S3 —відрізки шляху, пройдені відповідно за час t1,t2 і t3 з швидкостями υ1,υ2 і υ3. Проте за умовою задачі S1 = S2 + S3 і t2 = t3. Середня швидкість руху велосипедиста на другій половині шляху
S2
+ S3 буде ![]() (оскільки t2 = t3 ). Тому можна записати:
(оскільки t2 = t3 ). Тому можна записати:
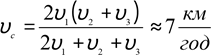 .
.
Відповідь: середня швидкість велосипедиста ≈ 7 ![]() км . год
км . год
Задача 78.
Ковзаняр біжить дистанцію S = 500м. Перші S1 =100м він біг з
швидкістю υ1 =10 ![]() м, наступні S2 = 300м з швидкістю
υ2 =11
м, наступні S2 = 300м з швидкістю
υ2 =11![]() м і с с
м і с с
останні S3 =100м з швидкістю
υ3 =13 ![]() м. Яка середня швидкість
бігу с
м. Яка середня швидкість
бігу с
ковзаняра?
Розв’язання:
Sυ1υ2υ3 м υс = ![]() ≈11,1
≈11,1 ![]() .
.
S1υ2υ3 + S2υ1υ3 + S3υ1υ2 с
Відповідь: середня швидкість бігу ковзаняра рівна ≈11,1![]() м. с
м. с
Задача 79.
Пропливаючи повз пункт А проти течії річки, моторний човен зустрів пліт. Через t1 =1год після зустрічі мотор човна заглух. Ремонт тривав t2 = 20хв, протягом якого човен вільно плив за течією з попередньою швидкістю відносно води і наздогнав пліт на відстані l = 7км від пункту А. Знайти швидкість течії річки υ.
Розв’язання:
Розглянемо рух човна в системі відліку, пов’язаній з плотом (течією річки). У цій системі човен протягом 1год віддалявся від плоту, потім 20хвперебував у спокої. Човен наздожене пліт за 1год, тому що його швидкість відносно води (і плоту) в обох випадках однакова. За t =1год +1год + 20хв = 2год20хв пліт проплив l = 7км, отже, швидкість течії:
l км
![]() υ= = 3 . t год
υ= = 3 . t год
Задачу можна розв’язати також у системі відліку, пов’язаній з берегом річки, прирівнявши час руху човна і плоту.
Відповідь: швидкість течії річки υ= 3 ![]() км .
км .
год
80.
Коли повз пристань проплив пліт у село, яке лежить на відстані
S1 =15км від пристані, вниз за течією відплив моторний човен. Він доплив до села за t = 45хв і, повернувся назад, зустрів пліт на відстані S2 = 9км від села. Визначити швидкість течії річки и і швидкість υ човна відносно води.
Розв’язання:
У системі відліку, пов’язаній з берегом річки, човен проплив
(υ+и)t1 за течією і (υ−u)t2 проти течії, а пліт проплив відстань u(t1 +t2 ). Очевидно, що (υ+u)t1 −(υ−u)t2 = u(t1 +t2 ), звідки t1 = t2 , тобто човен проти течії плив також 45хв. Для руху човна можна записати: (υ+u)t1 = S1 і (υ−u)t2 = S2 , звідки:
S1 + S2 км
υ= ![]() =16
=16 ![]() ,
,
2t1 год
![]() S1 − S2 км u = = 4 .
S1 − S2 км u = = 4 .
2t1 год
Відповідь: швидкість течії річки 4 ![]() км , швидкість човна
16
км , швидкість човна
16 ![]() км .
км .
год год
Задача 81.
Із Києва до Фастова з інтервалом часу t вийшли дві електрички, які рухаються з швидкостями υ. З якою швидкістю рухався потяг у Київ, якщо він зустрів ці електрички з інтервалом часу τ?
Розв’язання:
Відстань між електричками S =υt. З другого боку, ця відстань
S = (υ+ u)τ,
де u ![]() км — швидкість потяга.
Прирівнявши праві год
км — швидкість потяга.
Прирівнявши праві год
частини цих рівностей, дістанемо:
t −τ u =υ . τ
Відповідь: потяг рухався у Київ зі швидкістю u =υt −τ.
τ
Задача 82.
З пункту А, розташованого на кільцевій трасі, одночасно стартують в тому самому напрямі велосипедист і мотоцикліст (обидва рухаються рівномірно). Поки велосипедист пройшов перше коло, мотоцикліст пройшов три повні кола і прийшов в пункт В, де він обігнав велосипедиста перший раз. У скільки разів швидкість мотоцикліста більша від швидкості велосипедиста?
Розв’язання:
Позначимо довжину кола через d. Згідно з умовою задачі,
d + AB 3d + AB d AB
![]()
![]() = , звідки − = 2.
= , звідки − = 2.
AB d
З цього рівняння 2 +1. Тоді шукане відношення
AB
швидкостей:
υ2 d + AB
![]()
![]() = = 2+ 2.
= = 2+ 2.
υ1 AB
![]() Відповідь: швидкість мотоцикліста
більша від швидкості велосипедиста у 2 + 2
разів.
Відповідь: швидкість мотоцикліста
більша від швидкості велосипедиста у 2 + 2
разів.
Задача 83.
Колона автомобілів, довжина якої l = 2км, рухається з
швидкістю υ1 = 30 ![]() км . Від голови колони
до хвоста мотоцикліст год
км . Від голови колони
до хвоста мотоцикліст год
проїхав з швидкістю υ2 = 50 ![]() км , а в голову колони
повертався з год
км , а в голову колони
повертався з год
швидкістю υ3 = 60 ![]() км . Скільки часу затратив
на цю поїздку год
км . Скільки часу затратив
на цю поїздку год
мотоцикліст і який шлях він проїхав?
Розв’язання:
Систему відліку доцільно пов’язати з колоною автомобілів. Від
голови до хвоста мотоцикліст їхав протягом
часу: t1 =
![]() l і проїхав υ1 +υ2
l і проїхав υ1 +υ2
відстань S1 = l −υ1 1t = ![]() lυ2 , а від
хвоста до голови час руху υ1 +υ2
lυ2 , а від
хвоста до голови час руху υ1 +υ2
t2 =
![]() l ,
і пройдена відстань: S2 = l
+υ1 2t =
l ,
і пройдена відстань: S2 = l
+υ1 2t = ![]() lυ3 . На всю поїздку υ3 −υ1 υ3 −υ1
lυ3 . На всю поїздку υ3 −υ1 υ3 −υ1
![]()
![]() мотоцикліст затратив t =
l +
l = 5,5хв і проїхав
відстань: υ1 +υ2 υ3 −υ1 S = S1 + S2 =
l υ2 υ3 = 5,25 км.
мотоцикліст затратив t =
l +
l = 5,5хв і проїхав
відстань: υ1 +υ2 υ3 −υ1 S = S1 + S2 =
l υ2 υ3 = 5,25 км.
υ1 +υ2 +υ3 −υ1
Відповідь: мотоцикліст затратив 5,5 хв на відстань 5,25 км.
84.
Колона автомобілів виїжджає з певного пункту зі сталою
швидкістю υ1 = 36 ![]() км . У момент, коли голова
колони знаходилася на год
км . У момент, коли голова
колони знаходилася на год
відстані S =10км, з того самого пункту вирушає мотоцикліст з
швидкістю υ2 = 54 ![]() км і наздоганяє голову
колони, а потім год
км і наздоганяє голову
колони, а потім год
повертається в її хвіст, затративши на весь цей шлях t = 34хв. Визначити довжину колони, вважаючи, що вона не змінюється під час руху.
Розв’язання:
Пов’яжемо систему відліку з колоною. Мотоцикліст наздоганяє
голову колони
за час t1 =
![]() S і повертається в її
хвіст за час υ2 −υ1
S і повертається в її
хвіст за час υ2 −υ1
x
t2 =
![]() де x—довжина
колони. За умовою: t1
+t2 = t, тобто υ1 +υ2
де x—довжина
колони. За умовою: t1
+t2 = t, тобто υ1 +υ2
x S υ1 +υ2
![]() + = t, звідки x
=
+ = t, звідки x
= ![]() (υ2t −υ1t − S)=1км. υ1 +υ2 υ2 −υ1 υ2 −υ1
(υ2t −υ1t − S)=1км. υ1 +υ2 υ2 −υ1 υ2 −υ1
Відповідь: довжина колони 1 км.
Задача 85.
У плавальному басейні трьома доріжками пливуть спортсмени:
по першій і третій доріжках в один бік, а по другій — в протилежний. Швидкість першого спортсмена υ1, другого υ2. Знайти швидкість третьего спортсмена, якщо спортсмени весь час знаходяться на одній прямій і пливуть по середині доріжок. Відстань між серединами першої і другої доріжок d1,а між серединами другої і третьої d2.
Розв’язання:
![]() Систему відліку пов’яжемо з першим спортсменом.
У цій системі швидкість другого спортсмена υ1 +υ2 , а швидкість третього
υ1 +υ3. Умова, що вони
весь час знаходяться на одній прямій, зберігається.
Систему відліку пов’яжемо з першим спортсменом.
У цій системі швидкість другого спортсмена υ1 +υ2 , а швидкість третього
υ1 +υ3. Умова, що вони
весь час знаходяться на одній прямій, зберігається.
Нехай у певний момент часу спортсмени знаходяться в точках A, D і E. Через одиницю часу вони будуть у точках A, F і K ( перший спортсмен нерухомий у цій системі). Очевидно, що DF =υ1 +υ2 , а
υ1 +υ3 d1 + d2
![]() EK =υ1 +υ3. = ,
EK =υ1 +υ3. = ,
υ1 +υ2 d1
звідки:
d1 + d2 d2 υ3 = ![]() (υ1 +υ2 )−υ1 =
(υ1 +υ2 )−υ1 = ![]() (υ1 +υ2 )+υ2. d1 d1
(υ1 +υ2 )+υ2. d1 d1
Відповідь: швидкість третього спортсмена υ3 = ![]() d2 (υ1 +υ2 )+υ2. d1 Задача 86.
d2 (υ1 +υ2 )+υ2. d1 Задача 86.
Два теплоходи рівномірно
рухаються прямими курсами, які перетинаються під кутом α= 60°. Швидкості теплоходів
однакові і дорівнюють υ= 25 ![]() км . У початковий момент
часу теплоходи год
км . У початковий момент
часу теплоходи год
знаходилися в точках А і В, відстань між якими d = 50км. Визначити, через скільки часу відстань між теплоходами буде мінімальною і чому вона дорівнюватиме.
Розв’язання:
Нехай у якийсь момент часу t〉0 теплоходи знаходяться в точках
A1 і B1 .
Відстань між ними А1В1 = S знайдемо за теоремою косинусів:
2 2 2 α 2 α d 2 2 2 α
S
= d sin ![]() + 4cos
+ 4cos ![]() υt
−
υt
− ![]() ≥ d sin
≥ d sin ![]() ,
,
2 2 2 2
![]() d 2 оскільки завжди υt
−
d 2 оскільки завжди υt
− ![]() ≥ 0.
≥ 0.
2
Мінімальне значення S матиме при
такому
t, що υt −
![]() d = 0, звідки
d = 0, звідки
2
d
t
= ![]() =1год. Ця мінімальна
відстань
=1год. Ця мінімальна
відстань
2υ
Smin
= d
sin![]() =
25 км.
=
25 км.
Відповідь: через 1 годину відстань між теплоходами буде мінімальною і дорівнюватиме 25 км.
87.
Досягнувши швидкості υ0 =108 ![]() км , автомобіль починає год
км , автомобіль починає год
![]() рухатися рівносповільнено з прискоренням
а = 0,4
рухатися рівносповільнено з прискоренням
а = 0,4 ![]() м2 . Через який час с
м2 . Через який час с
його швидкість зменшиться в n = 3 рази?
Розв’язання:
Швидкість автомобіля через час t після початку сповільнення
υ=υ0 − at. Згідно з умовою
![]() υ0 = n, звідки: t
=
υ0 = n, звідки: t
=
![]() (n −1)υ0 = 50c.
(n −1)υ0 = 50c.
υ0 − at na
Відповідь: через 50 с швидкість автомобіля зменшиться в 3 рази.
Задача 88.
Мотоцикліст стартує з пункту О зі сталим прискоренням і проїжджає відстань АВ = S0 =125м між пунктами А і В за час t0 = 5c, причому його швидкість в пункті В була в n = 5 разів більша, ніж в А.
2S0(n −1)
![]() Довести, що
прискорення руху мотоцикліста а = 2 .
Довести, що
прискорення руху мотоцикліста а = 2 .
t0 (n +1) Визначити швидкість мотоцикліста в пунктах А і В, час, затрачений на рух до цих пунктів, а також відстань ОА.
Розв’язання:
Швидкість в пункті А знайдемо з формули шляху:
at02 n −1
S0 =υAt0 + ![]() =υAt0 + S0
=υAt0 + S0 ![]() ,
,
2 n +1
звідки
2S0 м
![]() υA = ≈ 8,33
υA = ≈ 8,33 ![]() . t0 (n
+1)
с
. t0 (n
+1)
с
Швидкість в пункті В:
2nS0 м
![]() υВ = nυA = ≈ 41,6
υВ = nυA = ≈ 41,6 ![]() .
.
t0 (n +1) с
Знаючи швидкість у точці А, можна з формули ![]() аS
знайти
аS
знайти
відстань S1 =
OA: S1
= ![]() 2S0 ≈ 5,2м, а з формули
S1 =
2S0 ≈ 5,2м, а з формули
S1 = ![]() at12 знайти час n −1 2 t 2 t0 руху мотоцикліста до пункту А:
at12 знайти час n −1 2 t 2 t0 руху мотоцикліста до пункту А:
![]() , або
t1 =
, або
t1 = ![]() =1,25c. Тоді
=1,25c. Тоді
(n −1) n −1
до пункту В мотоцикліст рухався t2 = t1 +t0 = 6,25c.
Відповідь: швидкість мотоцикліста в пункті А ≈8,33 ![]() м, в пункті с
м, в пункті с
м
В≈ 41,6 ![]() , відстань ОА≈5,2 м, час, затрачений
на рух до цих пунктів с
, відстань ОА≈5,2 м, час, затрачений
на рух до цих пунктів с
1,25 с і 6,25 с відповідно. Задача 89.
Два велосипедисти їдуть назустріч один одному.
Один з них, маючи швидкість υ1 =18
![]() км , піднімається рівносповільнено
вгору з год
км , піднімається рівносповільнено
вгору з год
![]() прискоренням а = 0,2
прискоренням а = 0,2 ![]() м, а другий,—
маючи швидкість υ2 =
5,4
м, а другий,—
маючи швидкість υ2 =
5,4 ![]() км , с год
км , с год
![]() рівноприскорено
спускається з прискоренням а =
0,2
рівноприскорено
спускається з прискоренням а =
0,2 ![]() м2 . Через який с
м2 . Через який с
час вони зустрінуться і яку відстань до зустрічі проїде кожен, якщо відстань між ними в початковий момент часу S0 =130м?
Розв’язання:
За початок системи координат візьмемо початкове положення першого велосипедиста і вісь Ох спрямуємо в напрямку швидкості
υ1. Рівняння руху велосипедистів запишемо так: х1 =υ1t −
![]() at 2 і
at 2 і
2 at 2
x2
= S0 −υ2t − ![]() . У
момент зустрічі x1 =
x2
або
. У
момент зустрічі x1 =
x2
або
2
υ1t − ![]() at
2 = S0 −υ2t −
at
2 = S0 −υ2t −
![]() at
2 , звідки
t =
at
2 , звідки
t = ![]() S0 = 20c. Шлях, пройдений
S0 = 20c. Шлях, пройдений
2 2 υ1 +υ2 кожним велосипедистом до зустрічі:
at 2
S1 =υ1t − ![]() = 60м,
= 60м,
2
at 2
S2 =υ2t + ![]() = 70м.
= 70м.
2
Відповідь: два велосипедисти зустрінуться через 20 с і перший велосипедист проїде до зустрічі 60 м, а другий 70 м. Задача 90.
Два автомобілі вирушили одночасно із села до
міста, відстань між якими становить 180 км. Один автомобіль прибув до міста
на 45 хв пізніше, ніж другий, оскільки його швидкість була на 20 ![]() км год менша.
3 якою швидкістю рухався кожний автомобіль?
км год менша.
3 якою швидкістю рухався кожний автомобіль?
Розв’язання:
Нехай швидкість першого автомобіля була х ![]() км , тоді год
км , тоді год
швидкість другого — (х
+ 20)
![]() км . Другий автомобіль
витратив на год
км . Другий автомобіль
витратив на год
шлях із села до міста ![]() 180 год, а перший
— 180
180 год, а перший
— 180![]() год, що на х + 20 х
год, що на х + 20 х
![]() 45хв =
45хв = ![]() 3 год
більше, ніж час руху другого. Тоді 180 −
180 = 3.
3 год
більше, ніж час руху другого. Тоді 180 −
180 = 3.
4 х х + 20 4
Розв’яжемо одержане рівняння:
180 180 3
![]() − =
; х х + 20
4
− =
; х х + 20
4
60 60 1
![]() − =
; х х + 20
4
− =
; х х + 20
4
1200 1
![]() = ;
= ;
х(х + 20) 4
х2 + 20х − 4800 = 0;
х(20 + х) ≠ 0. х2 + 20х − 4800 = 0, х1 = 60; х2 = −80.
Корінь —80 не задовольняє умови задачі. Отже, перший
автомобіль рухався зі швидкістю 60 ![]() км , а другий — 80
км , а другий — 80 ![]() км .
км .
год год
Відповідь: перший автомобіль рухався зі швидкістю 60
![]() км , а год
км , а год
другий рухався
зі швидкістю 80 ![]() км . год
км . год
Задача 91.
Моторний човен пройшов 21 км проти течії річки і 8 км за течією, витративши на весь шлях 2 год. Знайдіть швидкість човна в
стоячій воді, якщо швидкість течії річки становить1 ![]() км .
км .
год
Розв’язання:
Нехай х ![]() км —швидкість катера
у стоячій воді, тоді його год
км —швидкість катера
у стоячій воді, тоді його год
швидкість за течією дорівнює (х +1)
![]() км , а проти течії—(х
−1)
км , а проти течії—(х
−1)
![]() км .
км .
год год
21 8
![]() год—час
руху катера проти течії,
год—час
руху катера проти течії, ![]() год—час руху за х −1 х +1
год—час руху за х −1 х +1
течією. Оскільки на весь рух було затрачено 2 години, то маємо рівняння:
21 8
![]() + = 2;
+ = 2;
х −1 х +1
2х2 − 29х −15 = 0;
(х +1)(х −1) ≠ 0;
2х2 − 29х −15 = 0;
D = 961;
1
x
=15 або х = − ![]() .
.
2
Значення х =
−![]() не задовольняє умову задачі.
не задовольняє умову задачі.
Відповідь: швидкість човна в стоячій воді становить 15
![]() км . год
км . год
Задача 92.
З міста А в місто В виїхав велосипедист. Через 3 год із міста А виїхав мотоцикліст, який прибув у місто В одночасно з велосипедистом. Знайдіть швидкість мотоцикліста, якщо вона на км
45![]() більша
за швидкість велосипедиста, а відстань між містами А і год
більша
за швидкість велосипедиста, а відстань між містами А і год
В становить 60 км.
Розв’язання:
Нехай х ![]() км — швидкість велосипедиста,
тоді (х + 45)
км — швидкість велосипедиста,
тоді (х + 45)
![]() км — год год
км — год год
швидкість мотоцикліста.
![]() 60 год—час руху
велосипедиста, х
60 год—час руху
велосипедиста, х
60 ![]() год—час
руху мотоцикліста. Оскільки велосипедист рухався
год—час
руху мотоцикліста. Оскільки велосипедист рухався
х + 45 на 3 години довше, то маємо рівняння:
60 60
![]() − = 3;
− = 3;
х х + 45
60(х + 45)− 60х −3х(х + 45)
= 0;
![]() х(х
+ 45)
х(х
+ 45)
х2 + 45х −900
= 0;
![]() х(х
+ 45)
х(х
+ 45)
х2 + 45х −900 = 0;
(х + 45) ≠ 0.
х х2 + 45х −900 = 0, х = −60 або х =15.
х = −60 не задовольняє умову задачі. Отже, швидкість
велосипедиста 15 ![]() км , мотоцикліста 15+ 45 = 60
км , мотоцикліста 15+ 45 = 60 ![]() км . год год
км . год год
Відповідь:
швидкість мотоцикліста становить 60 ![]() км . год
км . год
Задача 93.
Перші 200 км дороги від А до В автомобіль проїхав із певною
швидкістю, а останні 150 км—зі швидкістю, на 20 ![]() км меншою. год
км меншою. год
Знайдіть швидкість автомобіля, з якою він проїхав останні 150 км, якщо на весь шлях від А до В він витратив 5 год. Розв’язання:
Нехай х ![]() км —швидкість автомобіля,
з якою він проїхав 150 км, год
км —швидкість автомобіля,
з якою він проїхав 150 км, год
при цьому затративши 150![]() год. Тоді (х
+ 20)
год. Тоді (х
+ 20)
![]() км —швидкість х год
км —швидкість х год
автомобіля, з якою
він проїхав перші 200 км, затративши ![]() 200 год. х + 20
200 год. х + 20
Оскільки на весь шлях було витрачено 5 годин, то маємо рівняння:
150 200
![]() + =
5; х х +
20
+ =
5; х х +
20
150(х + 20) + 200х −5х(х + 20)
![]() =
=
х(х + 20)
х2 −50х −600
![]() =
0;
=
0;
х(х + 20)
х2 −50х −600 = 0;
х(х + 20)≠ 0.
х2 −50х −600 = 0, х = −10 або х = 60.
х = −10 не задовольняє умову задачі. Отже, х = 60.
Відповідь:
швидкість автомобіля 60 ![]() км . год Задача 94.
км . год Задача 94.
З пункту А в пункт
в пункт В автомобіль їхав шосейною дорогою завдовжки 210 км, а повертався
з пункту В в пункт А по ґрунтовій дорозі завдовжки 160 км,
витративши на зворотний шлях на 1 год більше, ніж на шлях з пункту А
в пункт В. З якою швидкістю їхав автомобіль по ґрунтовій дорозі, якщо вона
на 30 ![]() км менша, ніж год
км менша, ніж год
його швидкість на шосе?
Розв’язання:
Нехай х ![]() км —швидкість автомобіля,
який їхав з А в В, тоді його год
км —швидкість автомобіля,
який їхав з А в В, тоді його год
швидкість на
ґрунтовій дорозі—(х −30)
![]() км .
км . ![]() 210 год—час, год х
210 год—час, год х
затрачений на
поїздку з пункту А до пункту В, ![]() 160 год—час, х
−30
160 год—час, х
−30
затрачений на поїздку з пункту В до пункту А. За умовою задачі,
160 210
![]() − =1;
х −30 х
− =1;
х −30 х
160х − 210х + 6300 − х2 + 30х
=
![]() х(х
−30)
х(х
−30)
х2 + 20х − 6300
= 0;
![]() х(х −30)
х2 + 20х − 6300 = 0,
х(х −30)
х2 + 20х − 6300 = 0,
х(х −30) ≠ 0. х2 + 20х − 6300 = 0, х = −90 або х = 70.
км
х
= 70 ![]() . Тоді
швидкість автомобіля на ґрунтовій
. Тоді
швидкість автомобіля на ґрунтовій
год
дорозі:70−30 =
40( ![]() км ). год
км ). год
Відповідь: автомобіль по ґрунтовій
дорозі їхав з швидкістю40 ![]() км . год
км . год
Задача 95.
Мікроавтобус запізнювався на 12 хв. Для того, щоб прибути у пункт призначення вчасно, він за 144 км від цього пункту збільшив
свою швидкість
на 8 ![]() км . Знайдіть початкову
швидкість год
км . Знайдіть початкову
швидкість год
мікроавтобуса.
Розв’язання:
Нехай х
![]() км —початкова швидкість,
(х +8)
км —початкова швидкість,
(х +8)
![]() км —кінцева год год
км —кінцева год год
швидкість мікроавтобуса. Щоб проїхати 144 км, він затратив би
144 144
![]() год, якщо б їхав із початковою швидкістю,
і
год, якщо б їхав із початковою швидкістю,
і ![]() год—із
х х +8 кінцевою
швидкістю. Маємо рівняння:
год—із
х х +8 кінцевою
швидкістю. Маємо рівняння:
144 144 1
![]() − = ;
− = ;
х х +8 5
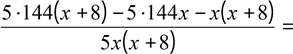
х
![]()
![]() 0;
0;
х2 +8х −5760 = 0,
х(х +8) ≠ 0,
х = −80 або х = 72.
х = −80 не задовольняє умову.
Відповідь: початкова швидкість мікроавтобуса рівна 72 ![]() км . год
км . год
Задача 96.
Перші 20 км шляху велосипедист рухався зі швидкістю, яка на км
5 ![]() більша
за швидкість, з якою він долав останні 20 км. З якою год
більша
за швидкість, з якою він долав останні 20 км. З якою год
швидкістю проїхав велосипедист другу половину шляху, якщо на весь шлях він витратив 3 год 20 хв?
Розв’язання:
Нехай х ![]() км —швидкість велосипедиста
на останніх 20 км, які год
км —швидкість велосипедиста
на останніх 20 км, які год
він проїхав за ![]() 20 год. Тоді перші
20 км він їхав зі швидкістю х
20 год. Тоді перші
20 км він їхав зі швидкістю х
км 20
(х +5) ![]() і затратив
на це
і затратив
на це ![]() год.
За умовою задачі маємо год х +5
рівняння:
год.
За умовою задачі маємо год х +5
рівняння:
20 20 1
![]() + =
3 ; х +5 х 3
+ =
3 ; х +5 х 3
60х + 60(х +5)−10х(х +5)
= 0;
![]() х(х
+5)
х(х
+5)
х2 −7х −30
![]() =
0; х(х +5)
=
0; х(х +5)
х2 − 7х −30 = 0,
х(х + 5) ≠ 0,
х2 − 7х −30 = 0, х = −3 або х =10.
х = −3 не задовольняє умову задачі. Отже, швидкість
велосипедиста
на другій половині шляху 10 ![]() км . год
км . год
Відповідь: велосипедист проїхав другу половину шляху з
швидкістю 10 ![]() км .
км .
год
Задача 97.
Турист проплив на моторному човні 25 км проти течії річки і повернувся назад на плоту. Знайдіть швидкість течії річки, якщо на плоту турист плив на 10 год більше, ніж човном, а власна швидкість
човна становить 12
Розв’язання:
Нехай х ![]() км —швидкість течії
річки, тоді (12−
х)
км —швидкість течії
річки, тоді (12−
х)
![]() км — год год
км — год год
швидкість човна проти течії. Проти
течії турист плив ![]() 25 год, а на 12 − х
25 год, а на 12 − х
плоту— ![]() 25 год. Маємо рівняння:
х
25 год. Маємо рівняння:
х
25 25
![]() − =10;
х 12 − х
− =10;
х 12 − х
25(12 − х)− 25х −10х(12 − х)
= 0;
![]() х(12
− х)
х(12
− х)
х2 −17х + 30
![]() 0; х(12 − х)
0; х(12 − х)
х2 −17х + 30 = 0;
х(12 − х) ≠ 0;
х = 2 або х =15.
х =15 не задовольняє умову задачі. Отже, швидкість течії річки
км
2 ![]() . год
. год
Відповідь:
швидкість течії річки становить 2 ![]() км . год
км . год
Задача 98.
Відстань між двома станціями, що дорівнює
420 км, потяг мав подолати за певний час. Коли він пройшов ![]() цієї відстані,
то
цієї відстані,
то
збільшив свою
швидкість на 5 ![]() км . З якою швидкістю
рухався потяг год
км . З якою швидкістю
рухався потяг год
на кожній ділянці руху, якщо на весь шлях він витратив 10 год? Розв’язання:
Нехай х ![]() км —швидкість потяга
на першій ділянці, довжина якої год
км —швидкість потяга
на першій ділянці, довжина якої год
складає ![]() . На подолання цієї відстані він затратив
. На подолання цієї відстані він затратив
240 км ![]() год. Зі швидкістю
(х +5)
год. Зі швидкістю
(х +5)![]() він подолав
решту шляху: х год
він подолав
решту шляху: х год
420− 240 =180(км)—за ![]() 180 год. Оскільки
на весь шлях було х +5
180 год. Оскільки
на весь шлях було х +5
затрачено 10 годин, то маємо рівняння:
240 180
![]() + =10,
х х +5
+ =10,
х х +5
240(х +5) +180х −10х(х +5)
![]() =
0;
=
0;
х(х +5)
х2 −37х −120
![]() =
0;
=
0;
х(х + 5)
х2 −37х −120 = 0,
(х + 5) ≠ 0.
х х2 −37х −120 = 0, х = −3 або х = 40.
х = −3 не задовольняє умову
задачі. Отже, швидкість потягу на першій ділянці становила 40 ![]() годкм , на другій—40 +5 =
45
годкм , на другій—40 +5 =
45![]() годкм .
годкм .
Відповідь: швидкість потяга на першій ділянці становить
40 ![]() км
, а швидкість на другій ділянці становить 45
км
, а швидкість на другій ділянці становить 45 ![]() км . год год
км . год год
Задача 99.
З міста А в місто В , відстань між якими дорівнює 320км, виїхав легковий автомобіль. Через 2 год після цього з В в А виїхала вантажівка, яка зустрілась з легковим автомобілем через 2 год після свого виїзду. Легкова долає відстань між містами А і В на 2 год 40 хв швидше, ніж вантажівка. Знайдіть швидкість кожного автомобіля. Розв’язання:
Нехай х ![]() км —швидкість легкового
автомобіля, у
км —швидкість легкового
автомобіля, у ![]() км — год год
км — год год
швидкість вантажівки. Вантажівка рухалася 2 год, легковий автомобіль 2+ 2 = 4(год) і вони проїхали 320 км. Маємо рівняння:
4х + 2у = 320. На весь шлях з А у В легковий автомобіль затратив
320 320 8 ![]() год, а вантажівка—
год, а вантажівка— ![]() год.
2год40хв =
год.
2год40хв = ![]() год.
За умовою задачі: х у 3
год.
За умовою задачі: х у 3
320 320 8
![]() − = . Маємо систему рівнянь:
у х 3
− = . Маємо систему рівнянь:
у х 3
4х + 2у = 320,
320 320 8
![]() у − х = 3;
у − х = 3;
у =160 − 2х,
320 320 8
![]() [1]160
− 2х − х = 3;
[1]160
− 2х − х = 3;
у =160 − 2х,
960х −960(160 − 2х)−8х(160 − 2х)
у =160 − 2х, 2
х +100х −9600
![]() х(160
− 2х) = 0;
х(160
− 2х) = 0;
у =160 − 2х, 2
х +100х −9600 = 0,
х(160 − 2х) ≠ 0, х2 +100х −9600 = 0, х = −160 або х = 60.
х = 60,
х = −160 не задовольняє умову задачі, тому у = 40.
Отже, швидкість легкового автомобіля 60 ![]() км ,вантажного год
км ,вантажного год
км
40 ![]() . год
. год
Відповідь: швидкість
легкового автомобіля 60 ![]() км ,вантажного год
км ,вантажного год
автомобіля
40 ![]() км . год
км . год
Задача 101.
Потяг мав пройти 64 км. Коли він проїхав 24 км, то був затриманий біля семафора на 12 хв. Тоді він збільшив швидкість на км
10![]() і прибув
у пункт призначення із запізненням на 4 хв. Знайдіть год
і прибув
у пункт призначення із запізненням на 4 хв. Знайдіть год
початкову швидкість потяга.
Розв’язання:
Нехай х ![]() км —початкова швидкість
потяга. 24 км він проїхав за год
км —початкова швидкість
потяга. 24 км він проїхав за год
24 1
![]() год. Біля семафора
він витратив 12хв =
год. Біля семафора
він витратив 12хв = ![]() год.
64− 24 = 40(км) х 5
год.
64− 24 = 40(км) х 5
![]() потяг проїхав зі
швидкістю (х +10)
км за 40 год. Потяг запізнився
потяг проїхав зі
швидкістю (х +10)
км за 40 год. Потяг запізнився
год х +10
на 4хв =
![]() год. За графіком він повинен був затратити
на весь шлях
год. За графіком він повинен був затратити
на весь шлях
64 ![]() год. За умовою задачі маємо рівняння:
х
год. За умовою задачі маємо рівняння:
х
24 1 40 64 1
![]() +
+ − = ; х 5 х +10
х 15
+
+ − = ; х 5 х +10
х 15
2 40 40
![]() + − = 0;
+ − = 0;
15 х +10 х
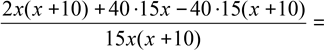 0;
0;
х
![]()
![]() 0;
0;
х2 +10х −3000 = 0,
х(х +10) ≠ 0,
х2 +10х −3000 = 0,
х = −60 або х = 50.
х = −60 не задовольняє умову задачі. Отже, початкова швидкість
потяга 50 ![]() км . год
км . год
Відповідь: початкова швидкість потяга становить 50
![]() км . год Задача
101.
км . год Задача
101.
Ескалатор метро піднімає пасажира, що стоїть нерухомо на ньому, протягом 1 хв. По нерухомому ескалатору пасажир піднімається пішки протягом 3 хв. Скільки часу витратить пасажир на підйом пішки по ескалатору, який рухається.
Розв’язання: Система відліку «Земля».
![]()
υ=υ1 +υ2 —швидкість пасажира в системі відліку «Земля» дорівнює сумі швидкостей його руху по ескалатору і швидкості ескалатора.
Для цієї системи відліку можна скласти наступні рівняння:
S =υ1 1t ,
S =υ2t2 ,
S = (υ1 +υ2 )t. Виразимо t з останнього рівняння::
S
t
= ![]() ,
,
υ1 +υ2
З перших двох рівнянь:
S S
υ1 = ![]() , υ2 =
, υ2 = ![]() . t1 t2
. t1 t2
Підставляємо:
S S 1 t t1 2 60⋅180
t = = = = = = 45(c).
![]() S S
1 1 t1 +t2 t1 +t2 60+180 t1 + t2 St1 + t2 t t1 2
S S
1 1 t1 +t2 t1 +t2 60+180 t1 + t2 St1 + t2 t t1 2
Відповідь: пасажир витратить 45 с на підйом пішки по ескалатору, який рухається. Задача 102.
Два брати вийшли в школу з певним часовим інтервалом, причому другий вийшов пізніше, тоді коли перший віддалився на 100
м по прямій дорозі. Швидкість першого брата 1 ![]() м, другого 2
м, другого 2 ![]() м.
м.
с с
Разом із другим братом вискочив собака, який бігав від другого брата
до першого і
назад зі швидкістю 5 ![]() м. Через який час другий брат с
м. Через який час другий брат с
дожене першого і який шлях пробіг собака?
Розв’язання:
Виберемо систему відліку «1-й брат». Час зближення:
S S 100м
![]() t
= = = =100с.
υ
υ2 −υ1 2 м −1 м с с
t
= = = =100с.
υ
υ2 −υ1 2 м −1 м с с
Шлях, пройдений за цей час собакою, дорівнює:
м
l3 =υ3t = 5 ![]() ⋅100с = 500м. с
⋅100с = 500м. с
Відповідь: другий брат наздожене першого через 100 с, а собака пробіг шлях, що становить 500 м.
Задача 103.
Автомобіль проїхав
30 км зі швидкістю 15 ![]() м, потім 40 км—за 1 с
м, потім 40 км—за 1 с
год. З якою середньою швидкістю рухався автомобіль на всьому шляху?
Розв’язання:
За умовою задачі рух автомобіля є нерівномірним, оскільки автомобіль змінив свою швидкість. Позначимо пройдений шлях, швидкість і час руху на першій ділянці l1, υ1 і t1, на другій— відповідно l2 , υ2 і t2. Згідно з цими позначеннями запишемо умову задачі.
![]() l l1 +l2 υсер = = . t t1 +t2
l l1 +l2 υсер = = . t t1 +t2
Аналізуючи умову задачі і формули середньої швидкості, бачимо, що нам невідоме t1. Його знаходимо по відомим l1 і υ1 :
l
t![]()
і зробимо підстановку в формулу середньої швидкості:
![]() l1 + l2 (3⋅104 + 4⋅104 )м
l1 + l2 (3⋅104 + 4⋅104 )м
![]() υсер = = 4 =
l1 3⋅10 3
υсер = = 4 =
l1 3⋅10 3
+ t2 ( + 3,6⋅10 )с
υ1 15
7⋅104 м 7⋅104 м м
![]() = ( 3 3 )
= 3 =12,5
= ( 3 3 )
= 3 =12,5 ![]() .
.
2⋅10 + 3,6⋅10 с 5,6⋅10 с с
Відповідь: автомобіль рухався на всьому шляху з швидкістю,
рівною 12,5
![]() м. с
м. с
Задача 104.
Потяг їхав 2 год
зі швидкістю 50 ![]() км , потім 0,5 години не год
км , потім 0,5 години не год
рухався, потім їхав 1 год зі швидкістю 100 ![]() км . Побудуйте
год
км . Побудуйте
год
графіки залежності пройденого шляху та швидкості від часу. Розв’язання:
Графік залежності шляху від часу являє собою ламану, оскільки на кожному з етапів руху швидкість потяга стала.
Кожний відрізок ламаної можна побудувати за двома точками. Наприклад, за перші 2 години потяг проїхав 100 км, тому, якщо вимірювати час в годинах, а відстань у кілометрах, координати кінців відповідного відрізка (0;0) і (2;100).
![]()
Весь час руху розіб’ємо на проміжки, протягом яких потяг рухався рівномірно. На кожному такому проміжку графік залежності швидкості від часу є відрізком, паралельним осі t.
Задача 105.
Автомобіль першу половину шляху рухався зі швидкістю
40 ![]() км , а другу —зі
швидкістю 60
км , а другу —зі
швидкістю 60 ![]() км . Яка середня швидкість
на год год всьому шляху?
км . Яка середня швидкість
на год год всьому шляху?
Розв’язання:
Аналізуючи умову задачі, треба звернути увагу на поняття «половина шляху». Воно означає, що весь шлях l можна подати як
суму двох рівних шляхів l1 і l2 тобто: l1 = l2 = ![]() l .
l .
2
Оскільки рух є нерівномірним, застосуємо формулу середньої швидкості для двох ділянок шляху відповідно до умови задачі:
![]() l l1 +l2 υсер = = . t t1 +t2
l l1 +l2 υсер = = . t t1 +t2
Аналізуючи умову задачі і формулу середньої швидкості, бачимо, що відсутні t1 і t2 . Знайдемо їх за відомими l1, υ1 і l2 , υ2 :
l1 l2 t1 = ![]() , t2 =
, t2 = ![]() . υ1 υ2
. υ1 υ2
У формулі середньої швидкості замість t1 підставимо його
значення ![]() l1 , а замість t2 −
l1 , а замість t2 − ![]() l2 : υ1 υ2
l2 : υ1 υ2
![]() l1 +l
υcее =.
l1 +l
υcее =.
1
υ1 υ2
Виконуємо підстановку в формулу середньої швидкості значень
l1
і l2 відповідно
до умови задачі l1 = ![]() l ,l2 =
l ,l2 = ![]() l :
l :
2 2 l l
![]() + υсер = 2 2 . l l
+ υсер = 2 2 . l l
![]() +
+
2υ1 υ2
Скорочуючи на l чисельник і знаменник, отримаємо:
1
![]() υсер =. 1 1 1
υсер =. 1 1 1
+
2υ1 υ2
Виконуючи дії над дробами, дістанемо такі співвідношення:
км км
![]() υсер = 2 = 2 =
2υ1υ2 = 2⋅40 год ⋅60 год = 48
υсер = 2 = 2 =
2υ1υ2 = 2⋅40 год ⋅60 год = 48 ![]() км
.
км
.
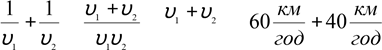 год
год
Відповідь: середня швидкість на всьому шляху становить
км
48 ![]() . год Задача 106.
. год Задача 106.
Радіус рукоятки колодязного коловорота в 3 рази більший за радіус валу, на який намотується трос. Яка швидкість кінця рукоятки при підйомі відра з глибини 10 м за 20 с?
Розв’язання:
Лінійна швидкість вала, на який намотується трос, дорівнює швидкості руху відра:
h
υ1 =υВ = ![]() (
)1
(
)1
t
При обертанні коловорота кутова швидкість кінця рукоятки дорівнює кутовій швидкості вала ω1 =ω2 , або
υ1 υ2
![]() = ,
= ,
R1 R2

Відповідь: швидкість кінця рукоятки становить 1,5 ![]() м. с Задача
107.
м. с Задача
107.
З човна вікінгів масою 500 кг, що рухається зі швидкістю
1 ![]() м, с
м, с
стрибає воїн масою 80 кг в горизонтальному напрямі зі швидкістю м
7 ![]() . Якою
буде швидкість човна після стрибка воїна, якщо він с
. Якою
буде швидкість човна після стрибка воїна, якщо він с
стрибає в сторону, протилежну рухові човна? Розв’язання:
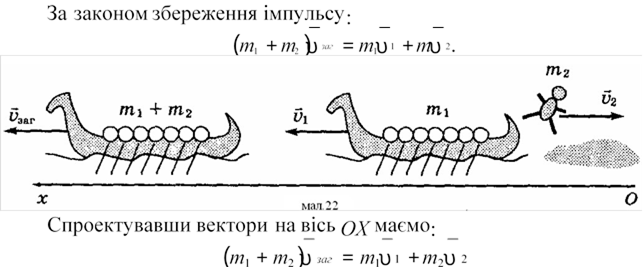
(m1 + m2 )υзаг = m1υ1 + m2υ2
Звідси:
m1υ1 = (m1 + m2 )υзаг + m2υ2.
м м
![]() 1 (m1 + m2 )υзаг + m2υ2 580кг ⋅1 с +80кг
⋅7 с . υ
= =
1 (m1 + m2 )υзаг + m2υ2 580кг ⋅1 с +80кг
⋅7 с . υ
= =
m1 500кг
Відповідь: швидкість човна після стрибка воїна становить м
2,28 ![]() . с
. с
Задача 108.
Пліт масою m1 вільно ковзає по поверхні води зі швидкістю υ1. На пліт з берега стрибає людина масою m2. Швидкість людини перпендикулярна швидкості плота і дорівнює υ2.
![]()
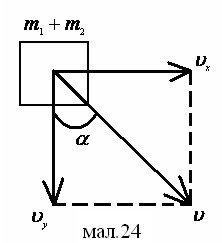
Визначити швидкість плота з людиною. Тертям плота об воду знехтувати.
Перший спосіб розв’язання За законом збереження імпульсу:
![]()
![]() m1υ1 + m2υ2 = (m1 + m2)υ.
У проекції на OX : m2υ2 =
(m1 + m2 )υx. У проекції на OY
:
m1υ1 + m2υ2 = (m1 + m2)υ.
У проекції на OX : m2υ2 =
(m1 + m2 )υx. У проекції на OY
:
m1υ1 = (m1 + m2 )υy,
![]() υ= υx2 +υy2 ,
υ= υx2 +υy2 ,
![]() υ=
υ= ![]() (m1υ1 )2 + (m2υ2 )2 .
(m1υ1 )2 + (m2υ2 )2 .
1 2
Другий спосіб розв’язання.
![]()
![]()
![]()
![]()
![]() m1υ1 + m2υ2 = (m1 + m2 )υ.
m1υ1 + m2υ2 = (m1 + m2 )υ.
![]() Отже,
(m1 + m2 )υ—діагональ
Отже,
(m1 + m2 )υ—діагональ
паралелограма зі сторонами m1υ1 і
За теоремою Піфагора:
![]() (m1 + m2 )υ= (m1υ1 )2 + (m2υ2 )2 , звідки
(m1 + m2 )υ= (m1υ1 )2 + (m2υ2 )2 , звідки
υ= (m1υ1 )2 + (m2υ2 )2 .
Відповідь: швидкість плота з
![]() людиною
виражається формулою υ=
людиною
виражається формулою υ=
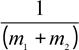 (m1υ1 )2 + (m2υ2 )2 .
(m1υ1 )2 + (m2υ2 )2 .
Задача 109.
Шофер побачив на
дорозі воронку від вибуху авіабомби на відстані 55 м від неї. Чи зможе він
зупинити автомашину до воронки, якщо початкова швидкість автомашини 60 ![]() км , час реакції шофера
год
км , час реакції шофера
год
0,9 с, час спрацювання гальмівної системи 0,3 с, а максимальне
прискорення внаслідок гальмування
-4,0 ![]() м ? с2 Розв’язання: Введемо такі позначення:
S0 = 55м; tр = 0,9с;
м ? с2 Розв’язання: Введемо такі позначення:
S0 = 55м; tр = 0,9с;
км
υ0 = 60 ![]() ;
;
год
tc = 0,3c; υ= 0;
м
a =
−4,0 ![]() 2 .
2 .
с
S1 —шлях, який пройшов автомобіль за час реакції шофера;
S2 —шлях, який пройшов автомобіль за час спрацювання
гальмівної системи;
S3 —шлях, який пройшов автомобіль за час гальмування; υ1 —швидкість автомобіля в кінці спрацювання гальмівної
системи.
1.Яку відстань пройде автомобіль до зупинки?
S = S1 + S2 + S3.
2.Яку відстань пройде автомобіль за час реакції шофера?
S1 =υ0tp.
3.Яку відстань пройде автомобіль за час спрацювання гальмівної системи?
atc2
S2 =υ0tc + ![]() .
.
4
4.Яку відстань пройде автомашина за час гальмування?
υt2 −υ12
S3 = ![]() .
.
2a
5.Яка швидкість автомобіля в кінці спрацювання гальмівної системи?
a
υ1 =υ0 + ![]() tc.
tc.
2
Підставивши у вихідну формулу значення невідомих величин, дістанемо вираз для шуканої величини:
2 atc 2
2 υt −υ0 +
![]() S
=υ0t p +υ0tc +
atc + 2 .
S
=υ0t p +υ0tc +
atc + 2 .
4 2a
Підставивши в нього числові значення величин в одиницях СІ, дістанемо розв’язок задачі: S ≈ 53м.
Відповідь: отже, шофер в змозі зупинити автомобіль, не доїхавши до воронки.
Задача 111.
На висоті h1 = 2м над серединою круглого стола діаметром
D = 3м висить лампа в I1 =100св. Цю лампу замінюють іншою лампою в I2 = 25св, змінивши відстань від стола так, щоб освітленість середини стола залишилась такою самою. Як зміниться освітленість краю стола?
Розв’язання:
1.Яка відстань від першої лампи до краю стола?
![]() l12 = h12 + r 2 ;
l12 = h12 + r 2 ;
![]() l1 = h12 + r 2 ; l1 = 22 +1,52 = 2,5м.
l1 = h12 + r 2 ; l1 = 22 +1,52 = 2,5м.
2.Чому дорівнює косинус кута падіння променів від першої лампи на край стола?
h1 2м
![]() cosα= = = 0,8.
cosα= = = 0,8.
l1 100св
3.Яка освітленість краю стола від першої лампи?
≈12,8лк.
4.Яка висота другої лампи над столом?
I1 I 2
![]() Е
= 2 = ; h
Е
= 2 = ; h![]()
h![]() ;
;
I1 100св h2 =1м.
5.Чому дорівнює відстань від другої лампи до краю стола?
![]() l22 = h22 +
r 2 ; l2 = h22 +
r 2 ; l2 =1,8м.
l22 = h22 +
r 2 ; l2 = h22 +
r 2 ; l2 =1,8м.
6.Чому дорівнює косинус кута падіння променів від другої лампи на край стола?
h2 1
![]() cosβ= = .
cosβ= = .
l2 1,8
7.Яка освітленість краю стола від другої лампи?
1
25св⋅
![]() I
2 cosβ 1,8
I
2 cosβ 1,8
Е2 = = ≈ 4,3лк.
l![]()
8.У скільки разів зменшилась освітленість краю стола?
E1 12,8лк
![]() n
= = ≈ 3рази.
n
= = ≈ 3рази.
E2 4,3лк
Відповідь: освітленість краю стола зменшилась приблизно в 3 рази. Задача 111.
Літак ІЛ—14 летить при боковому вітрі
з Новосибірська до Красноярська, відстань між якими по трасі 690км. Скільки
часу триватиме політ, якщо повітряна швидкість літака 360 ![]() км , а год
км , а год
швидкість
вітру 40 ![]() км ? год
км ? год
Розв’язання: Позначимо:
υ0 —швидкість вітру; υп —повітряна швидкість літака; υ—шляхова швидкість; t—час польоту літака.
Побудуємо паралелограм переміщень літака.
Тут υ0t —переміщення літака під дією вітру; υпt—переміщення літака під дією сили тяги двигунів; υt—переміщення літака відносно землі. Відповідно до теореми Піфагора:
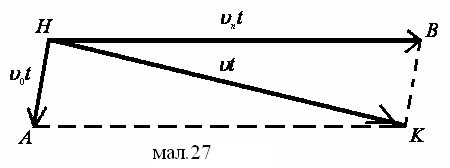
υ2t 2 +υ02t 2 =υп2t 2 =υп2t 2 ,
(3602 − 402 )t 2 = 6902 ,
звідки t =1год56хв.
Відповідь: політ триватиме близько 1год56хв.
Задача 112.
Човняр гребе, переміщуючись з швидкістю υ1 відносно води під кутом α до течії. Знаючи швидкість течії води, знайти результуючу швидкість човна.
Розв’язання:
Нехай швидкість течії води дорівнює υ2 .
![]() Побудуємо паралелограм
швидкостей. Оскільки човен бере участь одночасно в двох рухах, напрямлених під кутом
один до одного, то результуюча швидкість його дорівнює геометричній сумі його швидкостей.
Побудуємо паралелограм
швидкостей. Оскільки човен бере участь одночасно в двох рухах, напрямлених під кутом
один до одного, то результуюча швидкість його дорівнює геометричній сумі його швидкостей.
Треба знайти величину і напрям результуючої швидкості.
а)Знайдемо величину результуючої швидкості. За теоремою косинусів із трикутника ОВС маємо:
υ2 =υ12 +υ22 − 2υ1υ2 cosγ, υ2 =υ12 +υ22 − 2υ1υ2 cos(180°−α), υ2 =υ12 +υ22 + 2υ1υ2 cosα,
звідки
![]() υ= υ12 +υ22 + 2υ1υ2 cosα.
υ= υ12 +υ22 + 2υ1υ2 cosα.
б)Знайдемо напрям результуючої швидкості, тобто кут між
напрямом результуючої швидкості і берегами.
![]() За теоремою
синусів із трикутників ОВС , дістаємо: sinβ
За теоремою
синусів із трикутників ОВС , дістаємо: sinβ
![]() = ;
υ1
= ;
υ1
![]()
![]() = ,
= ,
або
![]() =
=
![]() .
.
Звідси
υ1 sinα sinβ=.
![]() υ12 +υ22 +
2υ1υ2 cosα
υ12 +υ22 +
2υ1υ2 cosα
Відповідь :результуюча швидкість човна напрямлена до берега υ1 sinα під кутом β, sinβ= , а її величина дорівнює
![]() υ12 +υ22 +
2υ1υ2 cosα
υ12 +υ22 +
2υ1υ2 cosα
υ12 +υ22 + 2υ1υ2 cosα.
Задача 113.
З Москви до Хабаровська
вирушає швидкий потяг, а через 40 хв за ним навздогін з пасажиром, що відстав
від потяга, відправляється автомобіль. З якою швидкістю повинен їхати автомобіль,
щоб наздогнати потяг на ст.Александров, розташованій на відстані 110 км від
Москви? Вважати, що швидкість руху потяга дорівнює 55 ![]() км , а год
км , а год
відстань залізницею така сама, як і автотрасою. Розв’язання:
1.За який час швидкий потяг пройде відстань Москва— Александров?
110км
= 2год.
км
![]() 55 год
55 год
2.За який час цю відстань повинен пройти автомобіль?
2 1 4
![]() 2− =1 = (год).
2− =1 = (год).
3 3 3
3.Скільки кілометрів за годину повинен проходити автомобіль, щоб наздогнати потяг?
4 110⋅3 км
![]() 110: = = 82,5
110: = = 82,5 ![]()
3 4 год
Розв’яжемо задачу алгебраїчно. S =110км;
t =
40хв = ![]() год;
год;
км
υп = 55 ![]() ;
;
год υав −?
Швидкість, з якою повинен їхати автомобіль:
S υав = ![]() .
.
tав
Час руху автомобіля:
tав = tп −t. Час руху потяга:
S
tп = ![]() . υп
. υп
Підставивши здобуті дані у вихідну формулу, матимемо:
S
![]() υав =.
υав =.
S
−t υп
Обчислимо швидкість, з якою повинен їхати автомобіль:
110 км
![]() υав = = 82,5
υав = = 82,5 ![]() 110 2 год
110 2 год
−
55 3
Відповідь: автомобіль, щоб наздогнати потяг на ст.Александров,
повинен їхати
з швидкістю82,5 ![]() км . год
км . год
Задача 114.
Визначити середню швидкість електропотяга на ділянці АС, якщо від пункту А до пункту В, що лежить на середині шляху, він
йшов з швидкістю
80 ![]() км , а від пункту В
до пункту С—з швидкістю год
км , а від пункту В
до пункту С—з швидкістю год
км
100 ![]() . год
. год
Розв’язання:
Нехай весь шлях АС позначимо через S, а повний час руху
електропотяга t розіб’ємо на t1 —час руху з швидкістю υ1 = 22,2 ![]() м і с
м і с
t2 —час руху з швидкістю υ2 = 27,7 ![]() м . Із означення середньої
год
м . Із означення середньої
год
![]() швидкості випливає, що υср =
S =
S .
(Не слід забувати, що t t1 +t2
швидкості випливає, що υср =
S =
S .
(Не слід забувати, що t t1 +t2
формула υср =![]() застосовується тільки
для рівномірного руху).
застосовується тільки
для рівномірного руху).
S S
![]()
Оскільки АВ = ![]() S і BC =
S і BC =
![]() S , то t1 = 2 , а t2 = 2 . Тепер
S , то t1 = 2 , а t2 = 2 . Тепер
2 2 υ1 υ2
підставимо ці значення в формулу середньої швидкості:
S 2υ1υ2
υср = = .
![]() S
+ S υ1 +υ2
S
+ S υ1 +υ2
2υ1 2υ2 Отримаємо:
м м
2⋅22,2 ⋅27,7
с с = 24,6 ![]() м.
м.
![]() (22,2
+ 27,7)м с
(22,2
+ 27,7)м с
с
Відповідь: середня швидкість електропотяга рівна 24,6 ![]() м. с
м. с
Задача 115.
Тіло стало рухатися рівноприскорено і за десяту секунду руху пройшло шлях 50 м. Знайдіть шлях, який пройшло тіло за дванадцяту секунду.
Розв’язання:
Спочатку знайдемо формулу шляху, яке пройшло тіло за довільну (n)—ту секунду рівноприскореного руху без початкової
швидкості. Нехай за час tn секунд шлях рівний
Sn =
![]() atn2 , а за час tn−1 2
atn2 , а за час tn−1 2
секунд— Sn−1 = ![]() atn2−1. Щоб знайти шлях, пройдений
за одну, а зокрема 2
atn2−1. Щоб знайти шлях, пройдений
за одну, а зокрема 2
(n)—ту секунду, тобто шлях S ( )n , слід від Sn відняти Sn−1. Тоді:
![]() S (
)
S (
)![]() = Sn −
Sn−1 = − atn2−1 = atn2 − a (tn −1)2 =
= Sn −
Sn−1 = − atn2−1 = atn2 − a (tn −1)2 = ![]() a[(2tn −1)]
a[(2tn −1)]
2 2 2 2 2
Отже, формула шляху за довільну (n)—ту секунду має вигляд:
S ( )n =
![]() a (2tn −1 .)
a (2tn −1 .)
2
В задачі дано шлях S (10) за десяту секунду (tn =10c)
S![]() .
.
Звідси знайдемо прискорення, з яким рухається тіло,
100м м a =
![]() 2 ≈ 5,26
2 ≈ 5,26 ![]() 2 .
2 .
19с с
Тепер можна знайти шлях S (12) , пройдений за дванадцяту секунду:
S (12) ≈ ![]() 5,26 м2 [(2⋅12 −1)с2 ]= 60,49м.
5,26 м2 [(2⋅12 −1)с2 ]= 60,49м.
2 с
Відповідь: шлях, який пройшло тіло за дванадцяту секунду становить ≈ 60,49 м. Задача 116.
З якою початковою швидкістю потрібно кинути на лід камінь,
щоб він, ковзаючи по його поверхні з прискоренням а = −0,5 ![]() м2 , с
м2 , с
зупинився на відстані 30 м від початку руху?
Розв’язання:
Використаємо формулу для рівносповільненого руху:
![]() S, чи
S, чи ![]() .
.
В даному випадку камінь зупинився (υ= 0), тому:
![]() υ02 = 2aS, чи υ0 = 2aS. Підставивши
значення отримаємо:
υ02 = 2aS, чи υ0 = 2aS. Підставивши
значення отримаємо:
м м
υ0 = 2⋅0,5 2 ⋅30м ≈ 5,44 ![]() . c с
. c с
Відповідь: камінь потрібно кинути з початковою швидкістю, яка
рівна 5,44 ![]() м. с Задача
117.
м. с Задача
117.
Товарний і пасажирський потяги рухаються назустріч один
одному. Товарний потяг, маючи швидкість υ01 = 54 ![]() км , почав год
км , почав год
сповільнювати свій рух з прискоренням
а1 = −1 ![]() м2 ; пасажирський , с
м2 ; пасажирський , с
рухаючись з швидкістю
υ02 = 36 ![]() км , став рухатися з
прискоренням год
км , став рухатися з
прискоренням год
м
а2 = 2 ![]() 2 . Через який час вони зустрінуться,
якщо в початковий с
2 . Через який час вони зустрінуться,
якщо в початковий с
момент вони знаходились на відстані 2 км один від одного?
Розв’язання:
Шлях, пройдений товарним потягом до зустрічі, можна виразити рівнянням:
![]() a1 t 2
a1 t 2
S1 =υ01t −,
2
а шлях, пройдений пасажирським потягом рівнянням
![]() a2 t2
a2 t2
S2 =υ02t +.
2
Відстань, пройдена потягами, рівна сумі S1 + S2 = 2000м, тобто:
![]() a1 t 2 a2t 2
a1 t 2 a2t 2
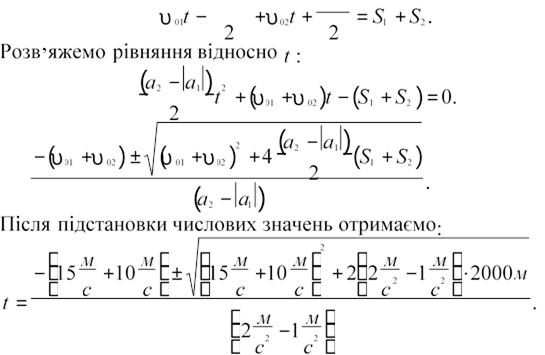 t =
t =
Маємо два значення: t1 = 43c;t2 = −93c. В якості відповіді приймаємо значення t1 = 43c. Від’ємне значення часу t2 = −93c відкидаємо, оскільки воно не має фізичного змісту.
Відповідь: товарний і пасажирський потяги зустрінуться через43с.
Задача 118.
Супутник обертається по круговій орбіті на висоті 1700 км над поверхнею Землі. Визначте швидкість супутника відносно Землі.
Радіус Землі рівний 6400 км.
Розв’язання:
Рівномірний рух супутника по круговій орбіті відбувається тільки під дією сили земного тяжіння:
mM
F
=γ ![]() 2 .
2 .
(R + H)
Ця сила змінює напрям вектора швидкості і в даному випадку являється доцентровою силою:
mυ2
F
= ![]() .
.
R + H
Прирівняємо праві частини рівності F =γ
![]() mM 2 і F =
mM 2 і F =
![]() mυ2 ,
mυ2 ,
(R + H) R + H
отримаємо:
mυ2 mM 2 M
![]() =γ 2 , або υ
=γ
=γ 2 , або υ
=γ ![]() .
.
R + H (R + H) R + H
Для визначення маси Землі скористаємось формулою g0 =γ![]() M2 ,
M2 ,
R
де g0 —прискорення вільного падіння біля поверхні Землі. Звідки
g0 R2
M = ![]() . Тоді
γ
. Тоді
γ
![]() 2 g0 R2
2 g0 R2
υ
= ![]() , звідки
υ= R . R + H
, звідки
υ= R . R + H
Враховуючи швидкість обертання Землі навколо своєї осі, швидкість супутника відносно Землі:
υс =υ±υЗ ,
де υЗ —лінійна швидкість точок земної поверхні на даній широті, яку можна знайти із співвідношення:
2πR
υЗ = ![]() ,
,
T
де T —період добового обертання Землі T = 24год; знайдемо:
![]() g0 2πR
υс = R ± . R + H T
g0 2πR
υс = R ± . R + H T
Знак «плюс» або «мінус» в останньому рівнянні беруть в залежності від того, запущений супутник зі сходу на захід чи з півночі на південь. Підставивши числові значення, отримаємо:
![]() υс = 6,4⋅106 м,
υс = 6,4⋅106 м,
υс′ ≈ 8000 ![]() м,υс′′≈ 6000
м,υс′′≈ 6000 ![]() м. с с
м. с с
Відповідь: швидкість супутника відносно Землі може становити
м м ≈ 8000 ![]() або ≈ 6000
або ≈ 6000 ![]() .
с с
.
с с
Задача 119.
Електроплитка має опір 240 Ом і споживає струм 5 А. Визначити вартість витраченої електроенергії за місяць, якщо 1кВт⋅год коштує 29 копійок, а плиткою користуються по 4 години на добу.
Розв’язання:
Для визначення вартості витраченої енергії спочатку визначають величину витраченої електроенергії:
А = I 2 Rt.
Підставивши числові значення дістанемо:
A = 25A2 ⋅240Ом⋅120год = 72000А⋅ А⋅Ом⋅год =
= 72000Вт⋅год = 72кВт⋅год.
Вартість 72кВт⋅год знайдемо з пропорції:
1кВт⋅год − 29коп.,
72кВт ⋅год − х;
Тоді
72кВт⋅год⋅29коп. х = ![]() = 20грн.88коп.
= 20грн.88коп.
1кВт⋅год
Відповідь: вартість витраченої електроенергії за 30 днів становить 20 грн. 88 коп.
Задача 120.
Два потяги йдуть назустріч один одному зі швидкістю: перший
36 ![]() км
, другий 54
км
, другий 54 ![]() км . Пасажир у першому потязі помічає, що год год
км . Пасажир у першому потязі помічає, що год год
другий потяг проходить повз нього протягом 6 с. Яка довжина другого потяга?
Розв’язання:
Вибираємо систему координат OS з початком відліку в точці О і пов’язуємо її з першим потягом. За початковий момент беремо час, коли початок другого потяга порівнявся з пасажиром, а координату відлічуватимемо від місця перебування пасажира.
Тоді закон руху початку другого потяга буде:
S =υвідн ⋅t,
де υвідн =υ1 +υ2 —швидкість другого потяга відносно першого.
Коли другий потяг пройде повз пасажира, його початок буде віддалений від пасажира на довжину цього потяга, тобто в цей момент S = l.Отже,
l =
(υ1 +υ2 )t
= 10 ![]() м +15
м +15 ![]() м⋅6с =150м.
м⋅6с =150м.
c с
Відповідь: довжина другого потяга 150 м.
Задача 121.
Літак у момент відривання від землі має швидкість 240 ![]() км і год
км і год
пробігає по бетонній доріжці відстань 790 м. Скільки часу триває розбіг і з яким прискоренням рухався при цьому літак? Рух вважати рівномірно-прискореним.
Розв’язання:
За умовою задачі розглядаємо відрізок шляху—рух літака по бетонній доріжці. Перед початком розбігу літак перебував у стані спокою, отже, його початкова швидкість дорівнювала нулю. Звідси можна дійти висновку: рух літака рівномірно-прискорений з початковою швидкістю, що дорівнює нулю. Щоб визначити час розбігу і прискорення, треба використати такі формули:
2 υ2
2aS
=υ
, звідки a =
![]()
2S;
υ
υ= at, звідки t
= ![]() .
.
a
Підставивши в формули числові значення величин і виконавши обчислення, знаходимо:
м2
66,7 ![]()
a
= с
≈ 2,8 ![]() м2 ;
м2 ;
2⋅790м с
66,7м⋅с2 t = ![]() ≈ 24с. с⋅2,8м
≈ 24с. с⋅2,8м
Відповідь: прискорення літака під час розбігу 2,8 ![]() м , час руху с2 24с.
м , час руху с2 24с.
Задача 122.
Автомобіль, який рухається зі швидкістю 30 ![]() км , можна год
км , можна год
зупинити гальмуванням за 2 с. Якого прискорення надають автомобілю гальма і яку відстань проходить він до зупинки?
Розв'язання
В умові сказано, що автомобіль зупиняється гальмуванням, отже, кінцева швидкість автомобіля дорівнює нулю. Рух автомобіля рівномірно-сповільнений з кінцевою швидкістю, що дорівнює нулю.
Записуємо формули цього руху і з них визначаємо прискорення і шлях:
υ0 υ0 = at, звідки a
= ![]() ,
,
t
at 2
S
= ![]() .
.
2 Підставивши числові значення, дістанемо:
8,3м м
а = − ![]() = −4,15
= −4,15 ![]() 2 ; с⋅2с с
2 ; с⋅2с с
4,15м⋅4с2
S = ![]() 2 = 8,3м с ⋅2
2 = 8,3м с ⋅2
Відповідь:
прискорення автомобіля −
4,15 ![]() м2 ; шлях, пройдений с
м2 ; шлях, пройдений с
до зупинки 8,3 м. Задача 123.
Вийшовши зі стану спокою, тіло рухалося рівномірноприскорено протягом 4 с, а потім наступні 6 с стало рухатися рівномірно і пройшло 18 м з тією швидкістю, якої воно набуло на кінець четвертої секунди. Визначити прискорення і шлях, пройдений тілом за весь час руху.
Розв’язання:
Тіло послідовно бере участь у двох рухах: спочатку воно рухається рівномірно-прискорено з початковою швидкістю, що дорівнює нулю (тіло вийшло зі стану спокою), а потім цей рух переходить у рівномірний. Кінцевою швидкістю рівномірноприскореного руху буде швидкість рівномірного руху:
υt =υпост.
Загальний шлях складається із суми двох шляхів: Sзаг = S1 + S2.
Шлях рівномірно-прискореного руху можна визначити з формули:
at12
S1 = ![]() ,
,
2
а шлях рівномірного руху визначимо з формули:
S2 =υпост ⋅t2.
Оскільки, υt = at1 =υпост , то, підставивши в S2 =υпост ⋅t2 значення швидкості, визначимо прискорення:
S2
S2 =υtt2 = at1 2t , звідки а
= ![]() .
.
t t1 2
Підставивши числові значення, дістанемо:
18м м
a
= ![]() = 0,75
= 0,75 ![]() 2 .
2 .
4с⋅6с с
Обчислимо шлях, пройдений тілом за перші 4с з S1 =
![]() at12 :
at12 :
2
S![]() .
.
Знаходимо загальний шлях: Sзаг = 6м +18м = 24м.
Відповідь: загальний шлях тіла в рівномірно-прискореному і рівномірному русі становить 24 м; прискорення в першій частині
руху становить 0,75 ![]() м . с2
м . с2
Задача 124.
Яка швидкість різання, якщо токар витрачає 56,6 с на обробку на токарному верстаті стального циліндра діаметром 0,006 м і завдовжки
0,7 м при подачі різця 0,5 мм за один оберт?
Розв’язання:
Знаючи довжину оброблюваного циліндра і крок подачі, можна визначити кількість обертів, зроблених циліндром за весь час обробки. Позначимо кількість обертів через n. Тоді:
l n = ![]() .
h
.
h
Час одного оберту, тобто період обертання циліндра, знаходимо за формулою:
t
T = ![]() , n
, n
де t —час, витрачений на обробку деталі.
Швидкість різання знайдемо з формули лінійної швидкості:
2πR πDn πDl 3,14⋅0,006м⋅0,7м −2 м
![]() υ= = = = −2 = 46,6⋅10
υ= = = = −2 = 46,6⋅10 ![]() .
.
T t th 56,6с⋅0,05⋅10 м с
Відповідь:
швидкість різання становить 46,6⋅10−2 ![]() м. с
м. с
Задача 125.
Не дочекавшись трамваю на зупинці А,
хлопчик вирушив до наступної зупинки В, Пройшовши ![]() шляху, він озирнувся
і помітив, що до зупинки А наближається трамвай. Якщо хлопчик у цей момент
побіжить до зупинки А або до зупинки В, то він прибіжить до кожної з них
одночасно з приходом туди трамваю. Визначити швидкість бігу хлопчика, вважаючи її
сталою (часом перебування трамваю на
шляху, він озирнувся
і помітив, що до зупинки А наближається трамвай. Якщо хлопчик у цей момент
побіжить до зупинки А або до зупинки В, то він прибіжить до кожної з них
одночасно з приходом туди трамваю. Визначити швидкість бігу хлопчика, вважаючи її
сталою (часом перебування трамваю на
зупинці А знехтувати), якщо швидкість трамваю дорівнює
30 ![]() км . год Розв’язання:
км . год Розв’язання:
Якщо хлопчик біжить до зупинки А, то він прибіжить туди одночасно з приходом трамваю. Оскільки хлопчик був від зупинки В удвічі далі, ніж від А, то, коли він побіжить до В і пробіжить півшляху, трамвай саме підійде до зупинки А. Після цього трамвай і хлопчик одночасно прибувають на зупинку В, але трамвай проходить при цьому шлях, утричі довший, ніж пробігає хлопчик. Отже,
швидкість хлопчика дорівнює 10
![]() км . год
км . год
Відповідь: швидкість бігу хлопчика рівна10 ![]() км . год Задача
127.
км . год Задача
127.
![]() У різні моменти часу
з пунктів А і В з сталими
У різні моменти часу
з пунктів А і В з сталими
швидкостями виїхали
назустріч один одному мотоцикліст і велосипедист. Зустрівшись у точці С, вони розвернулися і поїхали назад. Доїхавши до своїх початкових пунктів, гонщики розвернулися ї знову поїхали назустріч один одному. На цей раз вони зустрілися в точці D, знову розвернулися і т.д. В якій точці відбудеться їхня 1978-а зустріч?
Розв’язання:
Припустимо для конкретності, що велосипедист з пункту В виїхав раніше від мотоцикліста, і нехай у момент початку руху мотоцикліста він знаходився уже в точці В′. Відрізок шляху АВ′до зустрічі в точці С гонщики долали разом. Після зустрічі вони розвернулися і поїхали назад. Через певний час велосипедист знову знаходитиметься в точці В′, а мотоцикліст у точці А. Побудуємо точку В′′, симетричну точці В′ відносно точки В, і умовно перенесемо велосипедиста в цю точку. Враховуючи, що В′В = ВВ′′, можна тепер розглядати умовний рух мотоцикліста і велосипедиста вже назустріч один одному. Відрізок шляхуАВ′′ до зустрічі в точці D гонщики, таким чином, долатимуть разом. Після зустрічі вони розвернуться і через певний час мотоцикліст знову знаходитиметься в пункті А, а велосипедист буде в точці В′ (адже DB + BB′′ = DB + BB′) і рухатиметься в напрямі пункту А, тобто повториться ситуація, вже розглянута вище. Отже, третя зустріч знову відбудеться в точці С, четверта — в точці D і т.д., 1978-а зустріч гонщиків відбудеться, таким чином, в точці D.
Відповідь: зустріч відбудеться в точці D.
Задача 127.
Вздовж дороги розставлено світлофори на відстані 1км один від одного. У кінці кожної години протягом 1 хв на світлофорах горить червоне світло, забороняючи проїзд, а решту часу горить зелене світло. Мотоцикліст почав рух від світлофора, на якому тільки що спалахнуло зелене світло, і протягом 10 год їхав зі сталою швидкістю, ні разу не зупинившись і не порушивши правил (повз світлофор можна проїжджати і в той момент, коли там міняється світло). Яку найбільшу відстань міг проїхати мотоцикліст за цей час?
Розв’язання:
Протягом кожної
60-ї хвилини руху мотоцикліста на всіх світлофорах горітиме червоне світло. Тому
він не може проїхати за 1хв більше, ніж відстань між двома світлофорами, тобто
1 км. Отже, швидкість мотоцикліста не перевищує 1![]() км. Крім того, рухаючись
зі хв
км. Крім того, рухаючись
зі хв
км швидкістю 1 ![]() , проїжджатиме нові світлофори
або тоді, коли там хв
, проїжджатиме нові світлофори
або тоді, коли там хв
горить зелене світло, або тоді, коли колір світла міняється, а тому правил руху не порушуватиме. Таким чином, за 10 год мотоцикліст може проїхати щонайбільше 600 км.
Відповідь: найбільша відстань, яку міг проїхати мотоцикліст становить 600 км.
Задача 128.
Два мотоцикліст виїхали з міста В
в одному напрямі: перший—о 8 годині ранку, другий—о 10 годині 50 хвилин. Після того,
як другий мотоцикл наздогнав першого, вони продовжували шлях ще 2![]() год. В момент
зупинки виявилось, що другий мотоцикл обігнав першого на 30 км. Коли другий
мотоцикліст наздогнав першого і яку відстань пройшли мотоциклісти до цього, якщо
швидкість першого мотоцикліста дорівнює 0,6 швидкості другого?
год. В момент
зупинки виявилось, що другий мотоцикл обігнав першого на 30 км. Коли другий
мотоцикліст наздогнав першого і яку відстань пройшли мотоциклісти до цього, якщо
швидкість першого мотоцикліста дорівнює 0,6 швидкості другого?
Розв’язання:
І спосіб:
Нехай швидкість другого мотоцикліста 1, тоді швидкість першого мотоцикліста 0,6.
1)
10год50хв −8год
= 2год50хв, ![]() год йшов перший
до виходу другого.
год йшов перший
до виходу другого.
2)
![]() (частин) складає відстань, пройдена першим
(частин) складає відстань, пройдена першим
мотоциклом до виходу другого із В.
3) 1−0,6 = 0,4 (частин) наздоганяє за годину першого.
4)
1,7:0,4 = 4![]() (год)
за цей час другий мотоцикл наздожене першого.
(год)
за цей час другий мотоцикл наздожене першого.
5) 10год50хв + 4год15хв =15год5хв (в цей час другий наздогнав першого).
6)
![]() (частина) припадає на 30 км, тобто, швидкість
(частина) припадає на 30 км, тобто, швидкість
другого мотоцикліста 30 ![]() км . год
км . год
1 км
7)
30км⋅4 ![]() =127,5км—на такій
відстані від В другий
=127,5км—на такій
відстані від В другий
4 год
мотоцикл наздогнав першого. II спосіб:
1) х ![]() км
— швидкість другого мотоцикла, 0,6х
км
— швидкість другого мотоцикла, 0,6х ![]() км —швидкість год год
км —швидкість год год
першого мотоцикла, тоді
(х −0,6х)⋅2,5 = 30;
х = 30. км
30 ![]() —швидкість другого мотоцикла, год км
—швидкість другого мотоцикла, год км
18 ![]() —швидкість першого мотоцикла.
год
—швидкість першого мотоцикла.
год
2)
![]() —відстань, пройдена першим до виходу другого.
—відстань, пройдена першим до виходу другого.
км км км
3)
30 ![]() −18
−18 ![]() =12
=12 ![]() ; на
12 км другий наближається до год год год
; на
12 км другий наближається до год год год
першого за 1 годину.
км
4)
51км:12 ![]() = 4,25год — за цей час другий наздожене год
= 4,25год — за цей час другий наздожене год
першого.
км
5)
30 ![]() ⋅4,25год
=127,5км
— на такій відстані від В другий год
⋅4,25год
=127,5км
— на такій відстані від В другий год
наздожене першого.
Відповідь: другий мотоцикліст наздогнав першого о 15 год 5 хв, а відстань, яку пройшли мотоциклісти до цього, становить 127,5 км.
Задача 129.
О 9 годині 25 хвилин ранку пішохід відправився з пункту А в пункт В. Йдучи з однаковою швидкістю, він прибув в В о 13 годині 15 хвилин. На наступний день о 11 годині ранку він відправився із В в А, йдучи рівномірно, але дещо швидше, ніж він йшов перед цим, і прибув в А о 14 годині 40 хвилин. Знаючи, що відстань між пунктами 12 км, визначте, на якій відстані від А знаходиться те місце, через яке він проходив в один і той же час в кожен із цих днів? Розв’язання:
1) 13год15хв −9год25хв = 3год50хв—витратив пішохід на шлях від А до В.
2) 14год40хв −11год = 3год40хв—витратив пішохід на шлях від В до А.
5 3 км
3)
12км:3 ![]() год =
3
год =
3 ![]() —швидкість
на шляху від А до В.
—швидкість
на шляху від А до В.
6 23 год
2 3 км
4)
12км:3 ![]() год = 3
год = 3 ![]() —швидкість на шляху від
В до А.
—швидкість на шляху від
В до А.
3 11 год
5)
![]() — він йшов в перший день до 11 години.
— він йшов в перший день до 11 години.
6)
![]() — пройшов пішохід до 11 години ранку в перший день.
— пройшов пішохід до 11 години ранку в перший день.
22 1
7)
![]() 12− 4 = 7 (км)—відстань,
яку йому залишилось пройти з
12− 4 = 7 (км)—відстань,
яку йому залишилось пройти з
23 23
11 години.
Далі можна рахувати, що два пішоходи виходять одночасно (о 11 годині) із двох пунктів назустріч один одному, швидкості яких дані.
3 3 102 км
![]() 8)
3 +3 = 6 ( ) на
стільки кілометрів за годину вони
8)
3 +3 = 6 ( ) на
стільки кілометрів за годину вони
23 11 253 год
зближаються.
9) ![]() через такий час вони зустрінуться.
через такий час вони зустрінуться.
![]() —пройшов пішохід з 11 години до
—пройшов пішохід з 11 години до
зустрічі, коли йшов від А до В.
51 22
![]() 11)
3 + 4 = 8,4(км)—на такій
відстані від А знаходиться те
11)
3 + 4 = 8,4(км)—на такій
відстані від А знаходиться те
115 23
місце, через яке він проходив в один і той же час кожен із цих днів.
Відповідь: на відстані 8,4 км від А знаходиться те місце, через яке проходив пішохід в один і той же час в кожен із цих днів.
Задача 130.
![]() відстані між двома містами складає 75,25
км. О 5год 36 хв
відстані між двома містами складає 75,25
км. О 5год 36 хв
ранку із А в В виїхав велосипедист. О 7 год 15 хв ранку із В в А виїхав другий велосипедист, який проїжджав за годину на 0,75 км більше, ніж перший. Знайдіть швидкість кожного, якщо вони зустрілись опівдні.
Розв’язання:
1)
75![]() км =129км—відстань
від А до В.
км =129км—відстань
від А до В.
2)
12год −5![]() год = 6
год = 6![]() год— їхав перший
велосипедист до зустрічі з другим.
год— їхав перший
велосипедист до зустрічі з другим.
3)
12год −
7![]() год =
4
год =
4![]() год— їхав другий велосипедист до зустрічі
з першим.
год— їхав другий велосипедист до зустрічі
з першим.
4)
![]() —на стільки більше проїхав другий, ніж перший за
—на стільки більше проїхав другий, ніж перший за
![]() .
.
5)
![]() км—проїхали б обидва разом за той же час,
якби і другий їхав з швидкістю першого.
км—проїхали б обидва разом за той же час,
якби і другий їхав з швидкістю першого.
![]()
![]() 3
3
6)
6 год +
4 ![]() год =11 год—за
цей час перший велосипедист
год =11 год—за
цей час перший велосипедист
міг би проїхати 125![]() км.
км.
16
7 3 1 км
7)
125 ![]() км
:11
км
:11 ![]() год
=11
год
=11 ![]() —швидкість
першого
—швидкість
першого
16 20 4 год
велосипедиста.
1 км 3 км км
![]() 8)
11 + =12
8)
11 + =12 ![]() —швидкість
другого велосипедиста.
—швидкість
другого велосипедиста.
4 год 4 год год
Відповідь: швидкість першого велосипедиста дорівнює 11![]() 1 км ,
1 км ,
4 год
швидкість
другого велосипедиста 12 ![]() км . год
км . год
Задача 131.
Відстань між пунктами
А і В 114 км. О 6 годині із пункту А вийшов в напрямку
до В вантажний автомобіль, а о 6 год 45 хв назустріч йому вийшов
автобус з швидкістю на 8 ![]() км більшою, ніж год
км більшою, ніж год
швидкість вантажного автомобіля. Зустріч відбулася о 7 год 30 хв.
Знайдіть швидкості вантажного автомобіля і автобуса.
2)
6![]() год −
6год =
год −
6год = ![]() автобуса.
автобуса.
Розв’язання:
год—йшов вантажний автомобіль до виходу
км 3
3)
![]() 8
⋅ год = 6км пройшов автобус
більше, ніж вантажний год 4
8
⋅ год = 6км пройшов автобус
більше, ніж вантажний год 4
автомобіль за ![]() .
.
4) 114км − 6км =108км пройшли б вони, якби швидкості були рівними.
1 1
5)
7 ![]() −6 =1
−6 =1![]() (год)
— час руху вантажівки.
(год)
— час руху вантажівки.
![]() 2
2
1 3
6)
![]() 7 −6 =(год) — час руху
автобуса.
7 −6 =(год) — час руху
автобуса.
2 4 4
1 3 1
7)
![]() 1 + = 2 (год)—
за стільки часу вантажний автомобіль
1 + = 2 (год)—
за стільки часу вантажний автомобіль
2 4 4
може пройти 108 км.
1 км
8)
108:2 ![]() = 48
= 48 ![]() —швидкість вантажного автомобіля.
—швидкість вантажного автомобіля.
4 год
км
9)
48+8
= 56 ![]() —швидкість автобуса.
—швидкість автобуса.
год
Відповідь: швидкість вантажного автомобіля 48 ![]() км , швидкість год
км , швидкість год
автобуса 56 ![]() км . год
км . год
Задача 132.
Петро і Микола, які живуть на один від одного на відстані 840 м, о 9 год ранку вийшли назустріч один одному. Після зустрічі кожен з них продовжив рух в тому ж напрямі. Петро, дійшовши до будинку Миколи, одразу ж повернув назад, а Микола, дійшовши до будинку Петра, також повернув назад. Коли відбулася перша зустріч хлопців і
коли друга? Петро йшов весь час з швидкістю 50 ![]() м , а Микола 70
м , а Микола 70 ![]() м .
м .
хв хв
Розв’язання:
1) 50 + 70 =120(м) — на стільки зближувались хлопці за хвилину.
2) 840:120 = 7(хв)—через такий час вони зустрілись вперше.
3) 9год + 7хв = 9год7хв—в цей час відбулася перша зустріч.
4) 840⋅2 =1680(м)—таку відстань вони пройдуть разом від першої зустрічі до другої.
5) 1680:120 =14(хв)—через стільки хвилин після першої зустрічі хлопчики зустрінуться знову.
6) 9год7хв +14хв = 9год21хв—в цей час хлопці зустрінуться вдруге.
Відповідь: перша зустріч хлопців відбулася о 9 год 7 хв, друга зустріч відбулася о 9 год 21 хв. Задача 133.
Потяг за чверть хвилини проходить повз телеграфний стовп, а за
50 с—міст довжиною 0,7 км. Обчисліть середню швидкість руху потяга і його довжину.
Розв’язання:
50 км
1) 0,7: ![]() = 50,4
= 50,4 ![]() —швидкість потяга.
—швидкість потяга.
60⋅60 год
2) ![]() —довжина
потяга 210 м.
—довжина
потяга 210 м.
Відповідь: середня швидкість руху потяга становить
50,4 ![]() км , а год
км , а год
довжина потяга рівна 210 м.
Задача 134.
Я їду в потязі, який
їде з швидкістю 40 ![]() км , і бачу, як на протязі год
км , і бачу, як на протязі год
3с повз моє вікно в протилежному напрямі проходить швидкий потяг довжиною 75 м. З якою швидкістю йшов зустрічний потяг?
Розв’язання:
м
1)
75:3 = 25 ![]() —швидкість другого потяга
відносно мого
—швидкість другого потяга
відносно мого
с
потяга.
м 25⋅3600 км км
![]() 25 =
= 90
25 =
= 90 ![]() . с
1000 год год
. с
1000 год год
км
2)
90 − 40
= 50 ![]() —швидкість другого потягу.
—швидкість другого потягу.
год
Відповідь: зустрічний потяг йшов з швидкістю 50 ![]() км . год
км . год
Задача 135.
Із міста А в місто В вийшов вантажний автомобіль. В цей же час із міста В в місто А вийшов автобус. Зустріч відбулася на відстані 150 км від міста А. Знайдіть відстань від А до В, якщо відомо, що вантажний автомобіль може пройти весь шлях від А до В за 8год
30 хв, а автобус—за 7 год 30 хв.
Розв’язання:
1 2
1)
![]() 1:8 = —всього шляху проходить
вантажний автомобіль за
1:8 = —всього шляху проходить
вантажний автомобіль за
2 17
годину.
2)
![]() всього шляху проходить автобус за годину.
всього шляху проходить автобус за годину.
3)
![]() всього шляху проходять автобус і вантажний автомобіль
за годину.
всього шляху проходять автобус і вантажний автомобіль
за годину.
4)
![]() —через цей час машини зустрінуться.
—через цей час машини зустрінуться.
17⋅15 640 км
5)
![]() 150: = —швидкість
вантажного автомобіля.
150: = —швидкість
вантажного автомобіля.
64 17 год
6)
![]() —відстань від А до В.
—відстань від А до В.
Відповідь: відстань від А до В становить 320 км.
Задача 136.
Два літаки вилетіли одночасно з Москви в одному й тому ж
напрямі: один—з швидкістю 350 ![]() км , другий—з швидкістю
280
км , другий—з швидкістю
280 ![]() км .
км .
год год
Через дві години перший зменшив швидкість до 230 ![]() км . На якій год
км . На якій год
відстані від Москви другий літак наздожене першого?
Розв’язання:
км
1) 350− 280 = 70 ![]() —на стільки перший літак
відлітає від
—на стільки перший літак
відлітає від
год
другого за годину.
2) 70⋅2 =140(км)—на стільки перший літак відлетів від другого за 2 години.
км
3)280− 230 = 50 ![]() —на стільки кілометрів
за годину другий
—на стільки кілометрів
за годину другий
год
літак став зближуватися з першим.
4) 140:50 = 2,8(год)—через стільки годин другий наздожене першого після того, як змінилась швидкість першого.
5) 2+ 2,8 = 4,8(год)—стільки часу вони летіли до тих пір, поки другий наздогнав першого.
6) 280⋅4,8 =1344(км)—на такій відстані другий літак наздогнав першого.
Відповідь: другий літак наздожене першого на відстані 1344 км від Москви.
Задача 137.
Моторний човен повинен вийти із А
і прибути в В до визначеного часу. Якщо він буде їхати з швидкістю 35 ![]() км , то год
км , то год
запізниться на 2 години, якщо він буде їхати з швидкістю
50 ![]() км , год то прийде
на 1 годину раніше графіка. Яка відстань між містами А і В?
Скільки годин човен повинен був затратити на проходження шляху?
км , год то прийде
на 1 годину раніше графіка. Яка відстань між містами А і В?
Скільки годин човен повинен був затратити на проходження шляху?
Розв’язання:
км
1) 50 −35 =15 ![]() —різниця швидкостей.
—різниця швидкостей.
год
2) 50⋅1= 50(км)—на стільки більшу відстань АВ пройде човен за визначений час, проїжджаючи по 50 км за годину.
3) 35⋅2 = 70(км)стільки кілометрів не допливе човен до В, їдучи по 35 км за годину.
4) 50 + 70 =120(км)—на стільки більше пройде човен за визначений час, йдучи з більшою швидкістю.
5) 120:15 = 8(год)—визначений час.
6) 8−1= 7(год)—йшов човен
з швидкістю 50 ![]() км . год 7)
50⋅7 = 350(км)—відстань
від А до В.
км . год 7)
50⋅7 = 350(км)—відстань
від А до В.
Відповідь: відстань від А до В становить 350 км, а час, який човен повинен був затратити на проходження шляху, 8 годин.
Задача 138.
Один мотоцикліст виїхав із А в В, їдучи за годину 60,9 км; через
2
год із А в В виїхав другий мотоцикліст з швидкістю
40,6 ![]() км . За год
км . За год
скільки годин перший мотоцикліст завершить шлях із А в В, якщо другий приїхав в В на 7 год пізніше першого?
Розв’язання:
км
1)
60,9 − 40,6
= 20,3 ![]() —на стільки перший випереджає
—на стільки перший випереджає
год
другого за годину.
2) 7 − 2 = 5(год)—на стільки другий був в дорозі більше першого.
3) 40,6⋅5 = 203(км)—на стільки випередив перший мотоцикліст другого до моменту прибуття в В.
4) 203:20,3 =10(год) — за цей час перший пройшов відстань від
А до В.
Відповідь: перший мотоцикліст завершить шлях із А в В за 10 год.
Задача 139.
Робітник виїхав з пункту А о
4 год 30 хв ранку і приїхав в місто, коли було, без 10 хв
8 год ранку; якби він проїжджав за годину на 1,2 км менше, то їхав
би до міста 3![]() год. Скільки кілометрів від А до міста?
год. Скільки кілометрів від А до міста?
Розв’язання:
1) 7год50хв − 4год30хв = 3год20хв—був у дорозі робітник.
3 1 5
2)
![]() 3 −3 = (год)—на стільки
годин робітник був в дорозі
3 −3 = (год)—на стільки
годин робітник був в дорозі
4 3 12
менше.
3)
![]() — пройшов робітник за рахунок більшої швидкості
за
— пройшов робітник за рахунок більшої швидкості
за ![]() .
.
5 км
4)
4,5: ![]() =10,8
=10,8 ![]() —швидкість робітника.
—швидкість робітника.
12 год
5)
![]() —відстань від А до міста.
—відстань від А до міста.
Відповідь: відстань від А до міста 36 км.
Задача 140.
О 8 год ранку із пункту А вийшов автобус, а о 9 год із того ж пункту А і по тій же дорозі вийшов легковий автомобіль. Автобус, йдучи без зупинок, прибув в пункт В о 2 год дня, а легковий автомобіль —о 1 год 30 хв дня. На якій відстані від пункту А легковий автомобіль наздогнав автобус, якщо відомо, що його швидкість на км
20 ![]() більша швидкості автобуса?
більша швидкості автобуса?
год
Розв’язання:
1) 14год −8год = 6год—йшов автобус.
2) 13год30хв −9год = 4год30хв—був в дорозі легковий автомобіль.
3) 20⋅4,5 = 90(км)—на стільки більшу відстань пройшов легковий автомобіль, за 4,5 години ніж автобус (за рахунок великої швидкості).
4) 6− 4,5 =1,5(год)—на стільки годин автобус був в дорозі більше ніж легковий автомобіль.
км
5)
90км :1,5год =
60 ![]() —швидкість
автобуса. год
—швидкість
автобуса. год
км км км
6)
60 ![]() + 20
+ 20 ![]() = 80
= 80 ![]() —швидкість
легкового автомобіля. год год год
—швидкість
легкового автомобіля. год год год
7) 9 −8 =1(год)—на стільки годин раніше вийшов автобус і за цей час до виходу легкового автомобіля пройшов 60 км.
8) 60:20 = 3(год)—через стільки годин після виходу легкового автомобіля він наздожене автобус.
9) 80⋅3 = 240(км)—на такій відстані від пункту А легковий автомобіль наздожене автобус.
Відповідь: на відстані 240 км від пункту А легковий автомобіль наздогнав автобус.
Задача 141.
Щоб доставити телеграму за 2 год 40
хв із А в В, відстань між якими 70,5 км, листоноша їхав
спочатку на велосипеді з швидкістю 12,75 ![]() км , а потім на мотоциклі
з швидкістю 67,5
км , а потім на мотоциклі
з швидкістю 67,5 ![]() км . Скільки часу год год
їхав листоноша на велосипеді і скільки на мотоциклі? Розв’язання:
км . Скільки часу год год
їхав листоноша на велосипеді і скільки на мотоциклі? Розв’язання:
1)
![]() —проїхав би листоноша, якби всі 2 год 40
—проїхав би листоноша, якби всі 2 год 40
хв їхав на велосипеді.
2) 70,5−34 = 36,5(км)—відстань, яку він проїхав на мотоциклі за рахунок великої швидкості.
км
3)
67,5−12,75
= 54,75 ![]() —різниця швидкостей мотоцикла
і
—різниця швидкостей мотоцикла
і
год
велосипеда.
4)
36,5:54,75 =
![]() (год)—листоноша їхав на мотоциклі.
(год)—листоноша їхав на мотоциклі.
2 2
5)
![]() 2 − = 2(год)—
листоноша їхав на велосипеді.
2 − = 2(год)—
листоноша їхав на велосипеді.
3 3
Відповідь: листоноша їхав 2 год на велосипеді
і ![]() год
на
год
на
мотоциклі. Задача 142.
Пішохід і велосипедист відправляються одночасно і по одній дорозі
із міста А в місто В, яка знаходиться в 70 км від А.
Пішохід йде з швидкістю 3,75 ![]() км , велосипедист—15
км , велосипедист—15 ![]() км . Через скільки часу
між год год
км . Через скільки часу
між год год
ними буде відстань, рівна 30 км, і яку відстань до В залишиться тоді проїхати велосипедисту і пройти пішоходу?
Розв’язання:
км
1)
15−3,75
=11,25 ![]() —на таку відстань велосипедист
—на таку відстань велосипедист
год
випереджає пішохода на годину.
2)
30:11,25 =
2![]() (год)—через стільки часу відстань між
(год)—через стільки часу відстань між
велосипедистом і пішоходом буде 30 км.
3)
![]() —проїхав велосипедист.
—проїхав велосипедист.
4) 70− 40 = 30(км)—залишилось проїхати велосипедисту.
5) 30 +30 = 60(км)—залишилось пройти пішоходу.
Відповідь: відстань 30 км між
велосипедистом і пішоходом буде через 2![]() год; велосипедисту
залишиться проїхати 30 км, а пішоходу
год; велосипедисту
залишиться проїхати 30 км, а пішоходу
пройти 60 км.
Задача 143.
Почтовий потяг вийшов з станції о 7 год 25 хв ранку і йшов з
швидкістю 40,5 ![]() км . О 8 год
7 хв в тому ж напрямі відправився з цієї год
км . О 8 год
7 хв в тому ж напрямі відправився з цієї год
станції швидкий потяг. З якою швидкістю повинен йти швидкий потяг, щоб наздогнати поштовий на відстані 210,6 км від станції? Розв’язання:
1) 210,6:40,5 = 5,2(год)—пройде 210,6 км поштовий потяг.
2) 8год7хв
−7год25хв
= 42хв = ![]() год—на стільки
годин швидкий потяг був менше часу в дорозі, чим поштовий.
год—на стільки
годин швидкий потяг був менше часу в дорозі, чим поштовий.
3) 5,2 −0,7 = 4,5(год)—стільки часу потрібно швидкому потягу, щоб пройти 210,6 км.
км
4) 210,6:4,5 = 46,8 ![]() —швидкість швидкого потягу.
—швидкість швидкого потягу.
год
Відповідь: швидкість швидкого потяга рівна 46,8 ![]() км . год Задача
144.
км . год Задача
144.
На проходження шляху між двома пристанями теплоходу
потрібно на 40 хв більше, ніж катеру. Швидкість катера
40 ![]() км , а год
км , а год
теплохода —30
![]() км . Знайдіть відстань
між пристанями. год
км . Знайдіть відстань
між пристанями. год
Розв’язання:
I спосіб:
км
1) 40−30 =10 ![]() —різниця швидкостей катера
і теплохода. год
—різниця швидкостей катера
і теплохода. год
2) ![]() —пройде теплохід
за
—пройде теплохід
за ![]() год.
год.
3) 20:10 = 2(год)—за цей час катер пройде всю відстань.
4) 40⋅2 = 80(км)—відстань між пристанями.
II спосіб:
1)
Теплохід проходить 1 км за ![]() 1 год = 2хв.
1 год = 2хв.
2)
Катер проходить 1 км за  =1,5хв.
=1,5хв.
3) Теплоходу на 1 км шляху потрібно на 2−1,5 = 0,5(хв) більше, ніж катеру, а на весь шлях на 40 хв більше.
4) Отже, весь шлях між пристанями 40:0,5 = 80(км) Відповідь: відстань між пристанями 80 км.
Задача 145.
О 8 год 30 хв ранку із
двох пунктів виходять два автомобілі в одному напрямку. Автомобіль, який йде позаду,
проходить всю відстань між двома пунктами відправлення за 2![]() год, автомобіль,
що попереду, рухається в 2
год, автомобіль,
що попереду, рухається в 2![]() разів повільніше того, що позаду. Коли другий автомобіль
наздожене перший?
разів повільніше того, що позаду. Коли другий автомобіль
наздожене перший?
Розв’язання:
1 5
1)
![]() 1:2 = —відстань між двома
пунктами проходить другий
1:2 = —відстань між двома
пунктами проходить другий
5 11
за годину.
5 16 17
2)
![]() :2 = — тієї ж відстані
проходить перший автомобіль
:2 = — тієї ж відстані
проходить перший автомобіль
11 17 110
за годину.
5 17 3
3)
![]() − = — тієї ж
відстані за годину другий автомобіль
− = — тієї ж
відстані за годину другий автомобіль
11 110 10 наздоганяє перший.
3 1
4)
![]() 1: = 3 (год), тобто
за 3 год 20 хв другий автомобіль
1: = 3 (год), тобто
за 3 год 20 хв другий автомобіль
10 3
наздожене першого.
5) 8год30хв +3год20хв =11год50хв, тобто об 11 год 50 хв першого наздожене другий.
Відповідь: другий автомобіль наздожене першого об 11 год 50
хв. Задача 146.
Два спортсмени змагалися в бігу на одну й ту ж відстань.
Стартували вони в один й той же момент із одного пункту. Один пробіг всю дистанцію за 1 хв 15 с, а другий за 1 хв 20 с. Скільки метрів за хвилину в середньому пробіг кожен спортсмен, якщо через
48 с після старту між ними була відстань 20 м? Розв’язання:
1 4
1)
![]() 1:1 = всієї дистанції
проходить перший спортсмен за 1 хв.
1:1 = всієї дистанції
проходить перший спортсмен за 1 хв.
4 5
1 3
2)
![]() 1:1 = всієї дистанції
проходить другий спортсмен за 1 хв.
1:1 = всієї дистанції
проходить другий спортсмен за 1 хв.
3 4
4 3 1
3)
![]() − = на таку частину
дистанції перший спортсмен
− = на таку частину
дистанції перший спортсмен
5 4 20
випереджає другого за 1 хв.
4)
![]() .
.
![]() —на таку частину дистанції випередив перший
—на таку частину дистанції випередив перший
другого за 48 с.
5)
![]() —вся дистанція.
—вся дистанція.
4 м
6)
500⋅ ![]() = 400
= 400 ![]() —швидкість першого спортсмена.
—швидкість першого спортсмена.
5 хв 3 м
7)
500⋅ ![]() = 375
= 375 ![]() —швидкість другого спортсмена.
—швидкість другого спортсмена.
4 хв
Відповідь: швидкість першого спортсмена 400 ![]() м , швидкість хв
м , швидкість хв
другого спортсмена
375 ![]() м . хв
м . хв
Задача 147.
Відстань між пристанями на річці 43,2 км. Моторний човен, йдучи за течією річки, витрачає на цей шлях 2 год 24 хв. Скільки часу витрачає цей човен на цей же шлях, йдучи проти течії, якщо
швидкість течії
1,8 ![]() км ? год
км ? год
Розв’язання: км
1)
43,2км:2,4год =18 ![]() —швидкість
моторного човна за год
—швидкість
моторного човна за год
течією.
км км км
2)
18 ![]() −1,8
−1,8 ![]() ⋅2 =14,4
⋅2 =14,4 ![]() —швидкість
човна проти течії. год год год
—швидкість
човна проти течії. год год год
км
3)
43,2км:14,4 ![]() = 3год—витратить човен на цей же шлях,
год
= 3год—витратить човен на цей же шлях,
год
йдучи проти течії.
Відповідь: 3 год витратить човен на шлях, йдучи проти течії. Задача 148.
Теплохід, йдучи проти течії річки, пройшов відстань між пристанями за 9 год. Скільки часу потрібно теплоходу на зворотній шлях, якщо відстань між пристанями рівна 113,4 км, а швидкість течії
річки 1,9 ![]() км . год
км . год
Розв’язання: км
1)
113,4км:9год =12,6 ![]() —швидкість
теплохода проти течії. год
—швидкість
теплохода проти течії. год
км км км
2)
12,6 ![]() +1,9
+1,9 ![]() ⋅2 =16,4
⋅2 =16,4 ![]() —швидкість
теплохода за год год год
—швидкість
теплохода за год год год
течією.
км
3)
113,4км:16,4 ![]() ≈ 7год—знадобиться теплоходу, щоб пройти год
≈ 7год—знадобиться теплоходу, щоб пройти год
цю відстань за течією.
Відповідь: теплоходу потрібно 7 год на зворотній шлях.
Задача 149.
Велосипедист проїхав ![]() шляху і ще 40 км і йому
залишилось
шляху і ще 40 км і йому
залишилось
0,75 шляху без 118 км. Яка довжина шляху? Розв’язання:
5 2
1)
![]() 1− = всього шляху
залишилось пройти, коли ще не були
1− = всього шляху
залишилось пройти, коли ще не були
7 7
пройдені 40 км.
3 2 13
2)
![]() − = всього шляху
припадає на CD.
− = всього шляху
припадає на CD.
4 7 28
3) 118− 40 = 78(км) припадає на CD.
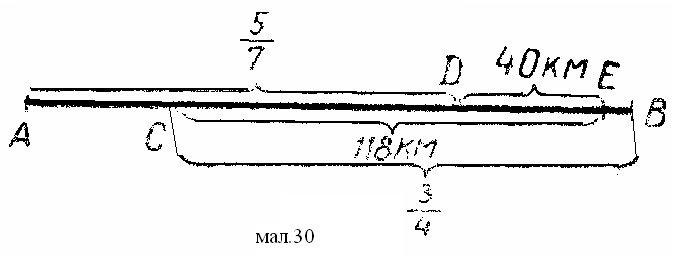
4)78:![]() =168(км)—відстань від А до В.
=168(км)—відстань від А до В.
Відповідь: відстань від А до В становить 168 км.
Задача 150.
Із міста А
в місто В приїхали двоє товаришів. Один із них 4 години їхав на велосипеді
з швидкістю 15 ![]() км і 6 годин на автомобілі.
год
км і 6 годин на автомобілі.
год
Другий 3 години їхав на потязі і 2 години на автомобілі (швидкості автомобілів однакові). Швидкість автомобіля в 2 рази менша швидкості потяга. Чому дорівнює відстань від А до В? Розв’язання:
км
1)
15 ![]() ⋅4год = 60км—проїхав
перший товариш на велосипеді.
⋅4год = 60км—проїхав
перший товариш на велосипеді.
год
2) Другий товариш їхав 3 години на потязі, швидкість якого в 2 рази більша швидкості автомобіля, отже, за 3 години він пройшов таку ж відстань, що й перший за 6 годин на автомобілі.
А оскільки вони проїхали одну й ту ж відстань (від А до В), то, така відстань, яку проїхав перший на велосипеді,—60 км—другий проїхав на автомобілі за 2 години.
км
60км:2год =
30 ![]() — швидкість
автомобіля. год км
— швидкість
автомобіля. год км
3)
30 ![]() ⋅6год
=180км—відстань,
яку проїхав перший на
⋅6год
=180км—відстань,
яку проїхав перший на
год
автомобілі.
4) 180км + 60км = 240км—відстань від А до В.
Відповідь: відстань від А до В рівна 240 км.
Задача 151.
Потяг повинен був пройти відстань між пунктами А і В за 11 годин 15 хвилин. Вийшовши із пункту А, потяг спочатку рухався з меншою швидкістю і пройшов 0,4 всієї відстані за 5 годин. Але потім
збільшив швидкість
на 10,8 ![]() км і прийшов в пункт
В без запізнення. год
км і прийшов в пункт
В без запізнення. год
Знайдіть відстань між пунктами А і В.
Розв’язання:
1) 11,25−5 = 6,25(год)—йшов потяг із збільшеною швидкістю.
2) 1−0,4 = 0,6 всього шляху потяг йшов з збільшеною швидкістю.
3) 0,6:6,25 = 0,096 всього шляху проходив потяг за годину після збільшення швидкості.
4) 0,4:5 = 0,08 всього шляху проходив потяг за годину спочатку.
5) 0,096−0,08 = 0,016 всього шляху складає 10,8 км.
6) 10,8:0,016 = 675(км)—весь шлях.
Відповідь: відстань між пунктами А і В становить 675 км.
Задача 152.
Потяг повинен був пройти 720 км за 14 годин 24 хвилини. Пройшовши 0,75 цього шляху, він затримався із-за ремонту на 16 хвилин. З якою швидкістю потяг повинен продовжувати шлях, щоб прийти до місця призначення вчасно?
Розв’язання:
1)1−0,75 = 0,25 всього шляху залишилось пройти після зупинки.
2) 720⋅0,25 =180(км) залишилось пройти після зупинки.
3) 14,4⋅0,25 = 3,6(год) повинен був їхати потяг останню чверть шляху.
4 1
4)
![]() 3,6
− = 3 (год)—за
стільки часу потяг повинен пройти
3,6
− = 3 (год)—за
стільки часу потяг повинен пройти
15 3
останню чверть шляху, щоб прийти вчасно.
1 км
5)
180:3 ![]() = 54
= 54 ![]() —з такою швидкістю потяг
повинен
—з такою швидкістю потяг
повинен
3 год
продовжувати шлях.
Відповідь: потяг повинен продовжувати шлях з швидкістю км
54 ![]() , щоб прийти до місця призначення вчасно.
, щоб прийти до місця призначення вчасно.
год
Задача 153.
Туристи здійснювали перехід на велосипедах
три дні. За перший день пройшли ![]() всього шляху без 2 км. Другого дня—половину шляху,
що залишився, без 3 км і третього—
всього шляху без 2 км. Другого дня—половину шляху,
що залишився, без 3 км і третього—![]() шляху, що залишився, і
шляху, що залишився, і
ще додатково 6 км. Скільки кілометрів проїхали туристи за три дні? Розв’язання:
8 1
1) ![]() 1− = другого залишку складає 6 км.
1− = другого залишку складає 6 км.
9 9
2) 6:![]() = 54(км)—проїхали
туристи третього дня.
= 54(км)—проїхали
туристи третього дня.
3) 54 −3 = 51(км)—половина першого залишку.
4) 51:0,5 =102(км)—перший залишок.
5) ![]() 102− 2 =100(км)—
102− 2 =100(км)— ![]() 2 всього
шляху 1− 1 = 2.
2 всього
шляху 1− 1 = 2.
3 3 3
6) 100:![]() =150(км)—весь шлях.
=150(км)—весь шлях.
Відповідь: туристи за три дні проїхали 150км. Задача 154.
Після зустрічі двох теплоходів один з них пішов на північ, а другий на захід. Через дві години після зустрічі відстань між ними була 60 км. Знайдіть швидкість кожного теплохода, якщо відомо, що
швидкість
одного з них була на 6 ![]() км більша швидкості другого. год
км більша швидкості другого. год
Розв’язання:
Нехай швидкість теплохода, що йде на північ, х ![]() км , а год
км , а год
теплохода, що йде
на захід, (х
+ 6)
![]() км . Так як напрями руху
год
км . Так як напрями руху
год
перпендикулярні, то за теоремою Піфагора:
(2х)2 + [2(х + 6)]2 = 602 ,
звідки х = −24 або х =18. Умову задачі задовольняє лише
х=18. Отже,
швидкість першого теплохода 18 ![]() км , тоді другого год
км , тоді другого год
км
18+ 6 = 24 ![]() .
.
год
Відповідь: швидкість першого теплоходу становить 18 ![]() км , а год
км , а год
швидкість
другого становить 24 ![]() км . год
км . год
Задача 155.
Собака, знаходячись в точці А, побіг за лисицею, яка була на відстані 30 м від собаки. Стрибок собаки дорівнює 2 м, стрибок лисиці—1 м. Собака робить два стрибки за той час, як лисиця робить три стрибки. На якій відстані від точки А собака наздожене лисицю?
Розв’язання:
Два стрибки собаки складають 4 м; 3 стрибки лисиці складають 3м. Звідси, коли собака пробігає 4 м, відстань між собакою і лисицею зменшується на 4м −3м =1м. Початкова ж відстань між ними в 30 разів більша. Отже, собака наздожене лисицю, коли пробіжить
4м⋅30 =120м.
Відповідь: собака наздожене лисицю на відстані 120 м від точки
А.
Задача 156.
Потяг вийшов з станції А на станцію
С через В. Ділянку від А до В він йшов з встановленою
швидкістю, а ділянку від В до С— із зменшеною на 25%. На зворотному
шляху ділянку від С до В він йшов з встановленою швидкістю, а ділянку
від В до А—з швидкістю, зменшеною на 25%. Скільки часу йшов потяг
від А до С, якщо відомо, що на ділянку від А до В він
затратив стільки ж часу, скільки на ділянку від В до С, і що на шлях
в напрямку від А до С він використав на ![]() години менше, ніж на зворотній
шлях (тобто від С
години менше, ніж на зворотній
шлях (тобто від С
до А)?
Розв’язання:
Позначимо через t час руху потяга від А до С (в годинах) і через
υ—встановлену
швидкість в
![]() км . За умовою, шлях АВ
пройдений год
км . За умовою, шлях АВ
пройдений год
за ![]() t год при швидкості υкм , а шлях ВС—за
t год при швидкості υкм , а шлях ВС—за
![]() t год при швидкості
t год при швидкості
2 год 2
км t t
0,75⋅υ . Отже, АВ =υ км і ВС = 0,75⋅υ км. За умовою, на год 2 2
зворотному шляху ділянку СВ було пройдено з швидкістю υ, а ділянку ВА—з швидкістю 0,75υ. Отже, ділянку СВ було пройдено за
![]() час , тобто за
час , тобто за ![]() 0,75t год,
а ділянку ВА—за υ
0,75t год,
а ділянку ВА—за υ![]() t :0,75υ,
тобто за
t :0,75υ,
тобто за
2 2
t ![]() год. За умовою: 2⋅0,75
год. За умовою: 2⋅0,75
![]()
![]() t,
t,
звідки t =10.
Відповідь: потяг йшов від А до С 10 годин.
Задача 157.
Велосипедисту потрібно було проїхати відстань в 30км. Виїхавши
на 3 хв пізніше назначеного терміну, велосипедист їхав з швидкістю, більшою
на 1 ![]() км , і прибув вчасно
на місце. Визначте год
км , і прибув вчасно
на місце. Визначте год
швидкість, з якою їхав велосипедист.
Розв’язання:
Вважатимемо, що велосипедист їхав з швидкістю υкм ; тоді год
швидкість, яка передбачалась, дорівнювала (υ−1)
![]() км . Фактично год
км . Фактично год
велосипедист був у дорозі ![]() год, а надавався термін
год, а надавався термін
![]() год.
За умовою:
год.
За умовою:
![]() −
−
![]() =
=
![]() ,
,
Звідки υ= 25 абоυ= −24.
Значення υ= −24 не задовольняє умову задачі.
Відповідь: швидкість, з якою їхав велосипедист, становить
км
25 ![]() . год
. год
Задача 158.
З двох міст, відстань між якими 650 км, відправляються два потяги назустріч один одному. Якщо обидва потяги виїдуть з міста одночасно, то вони зустрінуться через 10 годин. Якщо ж другий потяг відправиться на 4 години 20 хвилин раніше першого, то зустріч відбудеться через 8 годин після відправлення першого. Визначте середню швидкість кожного потяга.
Розв’язання:
Нехай швидкість
першого потяга х ![]() км , швидкість другого
год
км , швидкість другого
год
км
у ![]() . В першому випадку перший потяг пройде до
зустрічі 10хкм,
. В першому випадку перший потяг пройде до
зустрічі 10хкм,
год другий 10укм. Тобто,
10х +10у = 650.
В другому випадку перший потяг проїде до зустрічі
8хкм, а другий (який йшов 8год +
4год20хв =12![]() год)
пройде 12
год)
пройде 12![]() укм.
укм.
Тобто,
8х +12![]() у = 650.
у = 650.
Маємо систему рівнянь:
10х +10у = 650,
![]()
8х +12у = 650,
звідки х = 35, у = 30.
Відповідь: середня швидкість першого потяга 35 ![]() км , а середня год
км , а середня год
швидкість
другого потяга 30 ![]() км . год Задача 159.
км . год Задача 159.
Два потяги відправляються одночасно назустріч один одному з станцій А і В, відстань між якими 600 км. Перший з них приходить на станцію В на 3 години раніше, ніж другий на станцію А. В той час, коли перший проїжджає 250 км, другий проїжджає 200 км. Знайдіть швидкість кожного потяга.
Розв’язання:
Нехай швидкість першого потяга х ![]() км , а другого у
км , а другого у ![]() км . год год
км . год год
Відстань в
600 км перший потяг проходить за ![]() 600 год, а другий—за
х
600 год, а другий—за
х
600 ![]() год. За умовою: у
год. За умовою: у
600 600
![]() х + 3 =
х + 3 = ![]() у ,
у ,
![]() 250 = 200.
250 = 200.
х у
Розв’язавши систему, одержимо х=50, у=40.
Відповідь: швидкість першого потяга
50 ![]() км , а швидкість год
км , а швидкість год
другого потяга
40 ![]() км . год
км . год
Задача 160.
Дачник, який йшов
на потяг, пройшов за першу годину 3,5 км, і розрахував, що рухаючись з такою
ж швидкістю, він запізниться на 1 годину. Тому він шлях, що залишився проходив з
швидкістю 5 ![]() км і год прибув
на станцію за 30 хв до відправлення потяга. Визначте, який шлях повинен був
пройти дачник.
км і год прибув
на станцію за 30 хв до відправлення потяга. Визначте, який шлях повинен був
пройти дачник.
Розв’язання:
Якщо довжина шляху х км, то при швидкості 3,5 ![]() км дачник год
км дачник год
пройде цю відстань за ![]() х год. А оскільки він
запізниться на потяг на
х год. А оскільки він
запізниться на потяг на
3,5
годину, то в момент його виходу до відходу потяга залишалось
х
![]() −1год. Через годину
після виходу дачника залишалось до
−1год. Через годину
після виходу дачника залишалось до
3,5
відходу потягу
![]() х − 2год, а потрібно
було пройти цю відстань за
х − 2год, а потрібно
було пройти цю відстань за
3,5
х −3,5 1 ![]() год. Оскільки він
прийде за
год. Оскільки він
прийде за ![]() годдо
відходу потяга, то:
годдо
відходу потяга, то:
5 2
х х −3,5 1
![]()
![]() − 2 −
= , 3,5 5 2
− 2 −
= , 3,5 5 2
звідки х = 21.
Відповідь: дачник повинен був пройти шлях, рівний 21 км.
Задача 161.
Віддаль від Києва до Гостомеля по шосе 19 км. З Києва в
Гостомель виїхав велосипедист з деякою постійною швидкістю; через 15 хвилин після нього в тому ж напрямку вийшов автомобіль; він через 10 хв після виходу наздогнав велосипедиста і продовжував шлях до Гостомеля, де, не зупиняючись, повернув назад і через 50 хв після свого виходу із Києва зустрів велосипедиста вдруге. Визначте швидкості автомобіля і велосипедиста.
Розв’язання:
Нехай швидкість велосипедиста х ![]() км , а автомобіля у
км , а автомобіля у
![]() км.
км.
хв хв
Автомобіль пробув в дорозі 10 хв, а велосипедист 10+15 = 25хв, коли його наздогнав автомобіль. В цей момент відстані, пройдені ними, були однаковими. Отже, 25х =10у. Коли на зворотному шляху автомобіль зустрів велосипедиста, автомобіль пройшов 50укм, а велосипедист 65хкм. Ці відстані в сумі дають подвійну відстань від Києва до Гостомеля. Тому 65х +50у = 38. Розв’язуючи систему рівнянь, знаходимо х = 0,2; у = 0,5.
Отже, швидкість велосипедиста 0,2 ![]() км =12
км =12 ![]() км ; швидкість
км ; швидкість
хв год
автомобіля 0,5 ![]() км =
30
км =
30 ![]() км .
км .
хв год
Відповідь: швидкість
велосипедиста 12 ![]() км , швидкість год
км , швидкість год
автомобіля 30
![]() км . год Задача
162.
км . год Задача
162.
Теплохід йде з Києва до Дніпропетровська протягом двох діб, назад— протягом трьох діб. Визначте, скільки часу буде пливти пліт з Києва в Дніпропетровськ.
Розв’язання:
Нехай пліт пропливає відстань а км
від Києва до Дніпропетровська за х діб. Тоді його швидкість, що дорівнює
швидкості течії Дніпра— ![]() а км . За умовою, швидкість теплоходу, х
добу
а км . За умовою, швидкість теплоходу, х
добу
який йде за течією, рівна ![]() а км . Отже, швидкість
теплохода в 2 добу
а км . Отже, швидкість
теплохода в 2 добу
![]() стоячій
воді буде а − а км . А оскільки швидкість
руху теплохода
стоячій
воді буде а − а км . А оскільки швидкість
руху теплохода
2 хдобу
проти течії складає ![]() а км , то швидкість його в стоячій воді рівна
а км , то швидкість його в стоячій воді рівна
3 добу
а а км
![]() + . Маємо
рівняння:
+ . Маємо
рівняння:
3 хдобу
а а а а
![]() − = + , 2 х 3 х звідки х =12.
− = + , 2 х 3 х звідки х =12.
Відповідь: пліт буде пливти з Києва в Дніпропетровськ 12 діб. Задача 163.
Якщо людина з постійною швидкістю спускається по ескалатору, який йде вниз, вона проходить 30 східців ескалатора. Піднімаючись з тією ж швидкістю по ескалатору, що спускається, людина проходить 150 східців. Скільки східців при тій же швидкості руху людина пройде по нерухомому ескалатору?
Розв’язання:
Нехай довжина ескалатора (відстань, яку вгору і вниз проходить людина) рівна S , швидкість руху ескалатора і людини відповідно рівна U iV. Довжину ескалатора будемо вимірювати східцями (цим ми спростимо розв’язання задачі).
При русі вниз зі швидкістю U +V людина пройде відстань S за той же час, за який з швидкістю V пройде 30 східців. Перше рівняння системи:
S 30
![]() = . U +V V
= . U +V V
При русі вгору зі швидкістю V −U людина пройде відстань S за той же час, за який з швидкістю V пройде 150 східців. Друге рівняння системи:
![]() S 150 = . V −U V
S 150 = . V −U V
Маємо систему:
S 30
![]() U +V = V ,
U +V = V ,
![]() V
−SU = 150V .
V
−SU = 150V .
Розділивши перше рівняння системи на друге, отримаємо:
V −U 1 3
![]() = , звідки V =
= , звідки V = ![]() U.
Підстановка співвідношень між
U.
Підстановка співвідношень між
U +V 5 2
швидкостями в рівняння дає відповідь S = 50.
Відповідь: 50 східців. (В цій задачі система двох однорідних рівнянь з трьома невідомими, що дозволяє зменшити число невідомих).
Задача 164.
Дві людини, у яких один велосипед на двох, повинні потрапити із пункту А в пункт В, який знаходиться на відстані 40 км від пункту
А. Перша людина рухається пішки
з швидкістю 4 ![]() км ,на велосипеді год
км ,на велосипеді год
– зі швидкістю 30 ![]() км . Друга пішки – з
швидкістю 6
км . Друга пішки – з
швидкістю 6 ![]() км , на год год
км , на год год
велосипеді
– з швидкістю 20 ![]() км . За який найменший час вони год
км . За який найменший час вони год
можуть потрапити в пункт В (велосипед можна залишати без нагляду)?
Розв’язання:
Зробимо 2 дуже важливих висновки. Мінімальний час руху людей можливий тільки в одному випадку: обоє прибувають в кінцевий пункт одночасно. Нехай із 40 км перший пройде х км пішки, тоді (40− х)км проїде на велосипеді, а другий (40− х)км пройде пішки, а х км проїде на велосипеді. (Змінювати характер руху вони можуть скільки завгодно раз: від цього смисл задачі не змінюється).
![]() Нехай
перший знаходився в дорозі
x + 40−
xгод, а другий –
Нехай
перший знаходився в дорозі
x + 40−
xгод, а другий –
4 30
x 40− x
![]() + год.
Як було сказано вище, обоє повинні прибути пункт
+ год.
Як було сказано вище, обоє повинні прибути пункт
20 6
В одночасно. Складемо рівняння:
x 40 − x x 40 − x
![]() + = + ,
+ = + ,
4 30 20 6
із якого отримаємо, що x =16км. Найменший час, за який вони дістануться до пункту В, рівний
![]() x 40 − x x 40 − x t = + = + = 4,8.
x 40 − x x 40 − x t = + = + = 4,8.
4 30 20 6
Відповідь: найменший час, за який вони дістануться до пункту В
4,8 год. Задача 165.
Два спортсмени бігають по одній замкненій доріжці. Швидкість кожного стала, і на пробіг всієї доріжки один витрачає на 5 с менше ніж другий. Якщо вони почнуть пробіг з спільного старту одночасно і в одному напрямку, то будуть поруч через 30 с. Через який час вони зустрінуться, якщо побіжать одночасно зі спільної лінії старту в протилежних напрямках?
Розв’язання:
Нехай довжина замкнутої доріжки рівна s; на пробіг цієї доріжки перший спортсмен витрачає t с, а другий – (t + 5) с.
Очевидно, що швидкості спортсменів рівні відповідно v1 =
![]() s і
s і
t s v2 = ![]() . t
+ 5
. t
+ 5
Якщо спортсмени починають пробіг зі спільного старту одночасно і в одному напрямку, то вони будуть поруч, коли більш швидкий спортсмен обжене іншого спортсмена рівно на круг довжиною s. За умовою задачі складемо рівняння:
30s 30s
![]() − = s.
− = s.
t t + 5
Знайдемо додатний корінь рівняння. Після почленного ділення на s отримаємо, що t =10, тобто спортсмени пробігають доріжку відповідно за 10 с і 15 с.
Якщо спортсмени біжать назустріч один одному зі спільної лінії старту, то всю довжину доріжки вони пробіжать з швидкістю:
![]() s s м v1 + v2 = + .
s s м v1 + v2 = + .
10 15 с
Час забігу до зустрічі:
s 150
t = = = 6 с.
![]() + 25
+ 25
10 15
Відповідь: два спортсмени зустрінуться через 6с. Задача 166.
Точка рухається по прямій так, що її координата змінюється за законом x = t 2 − 4t +10(м), де t — час руху в секундах. Знайдіть координату точки для моменту часу t = 5 с. Знайдіть переміщення точки, здійснене за перші п’ять секунд руху, і відстань, пройдену за цей час.
Розв’язання:
Координата точки при t = 5:
x(5) = 25 − 20 +10 =15 м.
Початкова координата точки при t0 = 0:
x(0) =10 м. Переміщення знайдемо як різницю кінцевої і початкової координат точки:
x = x(5)− x(0) =15−10 = 5 м.
Знайдемо закон зміни швидкості з часом:
v =
x′ = (2t
− 4)
![]() м. с
м. с
Очевидно, що перші дві секунди руху точка рухається в сторону, протилежну напрямку осі Ox(v〈0), зупиняється (v(2) = 0), а потім рухається в напрямку координатної осі.
Знайдемо координату зупинки (повороту):
x(2)= 4 −8+10 = 6(м).
В перші дві секунди був пройдений шлях
![]()
![]() x(2)− x(0)
= 4(м)
x(2)− x(0)
= 4(м)
при зменшенні координати точки.
В наступні три секунди був пройдений шлях:
![]()
![]() x(5)− x(2)
= 9(м).
x(5)− x(2)
= 9(м).
Пройдена за п’ять хвилин відстань складає:
s = 4 +9 =13(м).
Відповідь: 5м; 13м.
II.ГЕОМЕТРІЯ
1.ПОДІБНІСТЬ ТРИКУТНИКІВ
Задача 1.
Вуличний ліхтар знаходиться на висоті 9 м над прямою горизонтальною доріжкою, по якій рухається перехожий, що має зріст 1м 80см. Яка довжина тіні перехожого, якщо він знаходиться на відстані 2м, 4м, 6м від основи ліхтаря ?
Розв’язання:
![]() З подібності трикутників маємо:
З подібності трикутників маємо:
9м 2м + х1 1
![]() = ,х1 =
= ,х1 = ![]() м
м
7,2 2м 2
9м 4м + х2
![]() = ,х2 =1м
= ,х2 =1м
7,2 4м
![]() 9м 6м + х3 3 = , х3 =
9м 6м + х3 3 = , х3 = ![]() м.
м.
7,2 6м 2
В цій задачі слід звернути увагу учнів на зв’язок між прямолінійним поширенням світла і утворенням тіні.
Відповідь: довжина тіні перехожого, якщо він знаходиться
на відстані 2 м, становить ![]() м; довжина тіні перехожого, якщо він знаходиться
на відстані 4м, становить 1 м; довжина тіні перехожого, якщо він знаходиться
на відстані 6 м, становить
м; довжина тіні перехожого, якщо він знаходиться
на відстані 4м, становить 1 м; довжина тіні перехожого, якщо він знаходиться
на відстані 6 м, становить ![]() м.
м.
Задача 2.(фізика і астрономія)
Видимі диски Сонця і Місяця мають приблизно однакові кутові розміри, тобто їх видно з Землі під однаковим кутом. Знайдіть діаметр Сонця, якщо відомо, що світло йде від Сонця до Землі 8хв, від Місяця до Землі 1с, а діаметр Місяця дорівнює 3500км (наведені дані приблизні).
Розв’язання:
Відстань від Землі до Сонця в 480 разів більша відстані від Землі до Місяця:
8 м
R
= 3⋅10 ![]() ⋅480с,
⋅480с,
с
.
8 м
R
= 3⋅10 ⋅10 ![]() ⋅1с.
⋅1с.
с
З подібності трикутників АОВ і АО1В1 (мал.32).випливає, що
![]() В1О1 480
В1О1 480
![]() = , ВО 1
= , ВО 1
В1О1 = 480⋅1750км = 840000км.
D = 2R =1,68⋅106 км.
Відповідь: діаметр Сонця становить 1,68 млн.км.
Задача 3. За графіком швидкості тіла визначте:
а) рівняння швидкості;
![]() б) відношення відстаней, що
пройшло тіло за 6с і 8с.
б) відношення відстаней, що
пройшло тіло за 6с і 8с.
Розв’язання:
а) υ= 2t.
υ м
б) а = ![]() = 2(
= 2( ![]() 2 ), (а = tgϕ= 2). t с
2 ), (а = tgϕ= 2). t с
S6 62 9 S6 122 9
![]()
![]() в)
= 2 = або = 2 = .
в)
= 2 = або = 2 = .
S8 8 16 S8 16 16
Відповідь: площі подібних трикутників пропорційні квадратам відповідних сторін).
Задача 4.
Більярдна куля знаходиться в точці М. Розміри більярдного столу подані на мал.16. Під яким кутом потрібно направити кулю, щоб попасти в лузу N відбиванням її від двох бортів? Рух кулі вважати рівномірним і що при ударі кут падіння дорівнює куту відбивання.
Розв’язання:
![]() З подібності трикутників ABN і
З подібності трикутників ABN і
![]() ACM
випливає, що BN = AN ,
ACM
випливає, що BN = AN ,
CM AM
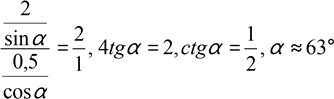 .
.
Відповідь: кулю потрібно направити під кутом α≈ 63°, щоб попасти в лузу N відбиванням її від двох бортів.
2.ПЛОЩІ МНОГОКУТНИКІВ
|
S = a⋅b |
|
|
|
S =υ⋅t |
|
|
|
S = a⋅h |
|
|
|
U = I ⋅R
S = n⋅h,де n—середня лінія трикутника |
|
|
|
A = N ⋅t |
|
|
|
S = n⋅h |
|
|
|
P =U ⋅ I |
|
|
|
S =υсер ⋅t;
S |
. |
|
|
S =υсер ⋅t,
υ=υ0 + a⋅t, S
|
|
|
|
|
||
Задача1.
Від потяга, що рухається, на ходу відчіплюють останній вагон. Потяг продовжує рухатися з попередньою швидкістю, а останній вагон - рівносповільнено. Порівняйте шляхи, що пройшли потяг і вагон до моменту зупинки вагона.
Розв’язання:
![]() Нехай до зупинки вагона минуло t секунд. Площа прямокутника
ОАВС відповідає пройденому шляху, а площа трикутника ОАС – шляху,
що пройшов вагон до зупинки (мал. 35).
Нехай до зупинки вагона минуло t секунд. Площа прямокутника
ОАВС відповідає пройденому шляху, а площа трикутника ОАС – шляху,
що пройшов вагон до зупинки (мал. 35).
1
S∆ОАС = ![]() SOABC .
SOABC .
2
Відповідь: Вагон пройшов шлях вдвічі менший за шлях потягу.
Задача 2.
Ліфт рівноприскорено піднімається протягом трьох секунд,
досягаючи
швидкості 4 ![]() м. З цією швидкістю ліфт
рухається 6с. с
м. З цією швидкістю ліфт
рухається 6с. с
Останні дві секунди він рухається рівносповільнено. Визначте висоту підйому ліфта.
Розв’язання:
![]() Висота підйому ліфта
дорівнює площі трапеції:
Висота підйому ліфта
дорівнює площі трапеції:
h ![]() .
.
Відповідь: висота підйому ліфта 34 м.
Задача 3.
Автомобіль рухається рівноприскорено зі швидкістю υ0 =0. На
першому кілометрі
його швидкість зростає на 10 ![]() м, на другому—на с
м, на другому—на с
м
5 ![]() . Скільки часу затрачено на проходження першого
кілометра?
. Скільки часу затрачено на проходження першого
кілометра?
с
другого кілометра?
Розв’язання: (мал.37)
![]() 1км=1000м.
1км=1000м.
![]() ,
,
t1 = 200.
![]() ,
,
t2 −t1 = 80.
Відповідь: на проходження першого кілометра затрачено200с, а на проходження другого кілометра затрачено 80с.
Задача 4.
Обчисліть роботу, виконану при стисненні пружини на 15 см, якщо відомо, що діюча сила пропорційна стисненню пружини і що для стиснення на 1 см необхідна сила 30 Н. (Задача на закон Гука
![]() F = k ⋅ x ).
F = k ⋅ x ).
Розв’язання:
Величина шуканої роботи чисельно рівна площі трикутника OMN (мал.38).
Спосіб 1.
А ![]() ,75 кДж
,75 кДж
Спосіб 2.
0,15 3000x 2 0,15
А
= ∫300хdx
= ![]() I0 =
I0 =
![]() 2
2
Відповідь: робота, виконана при стисненні
пружини, рівна 33,75Дж.
3.ПЕРЕМІЩЕНЯ ТА ЙОГО ВЛАСТИВОСТІ
В геометрії рухом називають перетворення площини (простору) зі збереженням розмірів і форми фігури. В геометрії ми розглядаємо лише початкове і кінцеве положення фігури. Рух в механіці—це безперервний процес з урахуванням ряду характеристик (швидкість, прискорення, сила, маса і ін.). (В більш широкому розумінні рух – це довільна зміна в просторі і часі.).
![]() Розглянемо три приклади осьової симетрії (мал.39-
Розглянемо три приклади осьової симетрії (мал.39-
41):
Коливання маятника (мал.39).
Відбивання світла і звуку (мал.40).
Траєкторія тіла, кинутого під кутом до горизонту (мал.41)
Паралельне
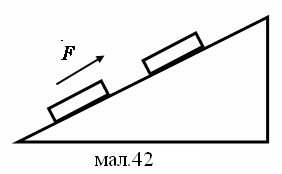
русі всі точки тіла описують однакові траєкторії, а
пряма, що з’єднує довільні дві точки тіла, переміщується згідно свого початкового напрямку.
Можна розглядати рух тіла по похилій площині як приклад поступального руху(мал.42).
Задача 1.
Годинникова і хвилинна стрілки співпадають опівночі. О котрій годині нового дня вперше знову співпадуть годинникова і хвилинна стрілки?
Розв’язання:
Дійсні повороти пов’язані з обертальним рухом твердого тіла і рухом по колу.
Кутова швидкість хвилинної стрілки в 12 раз більша, ніж кутова швидкість годинникової стрілки (мал.43):
![]() ϕ1 =
ϕ1 = ![]() - кут повороту годинникової
стрілки,
- кут повороту годинникової
стрілки,
ϕ2 = 2π+ ![]() - кут
- кут
повороту хвилинної стрілки.
Відповідь: приблизно о 1год5хв30снового дня вперше знову співпадуть годинникова і хвилинна стрілки. Задача 2.
З якою швидкістю повинен летіти літак з заходу на схід на екваторі і на широті 60°, щоб пасажирам цього літака Сонце здавалося нерухомим на небі?
Розв’язання:
![]() Удавана нерухомість Сонця досягається
при рівності швидкостей руху літака і Землі
Удавана нерухомість Сонця досягається
при рівності швидкостей руху літака і Землі
(мал.44):
2π⋅6400км км м
а)υ1 = ![]() =1660
=1660 ![]() ≈ 460
≈ 460 ![]() ;
;
24год год с
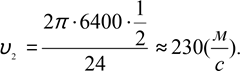
1
r − Rcos60° = ![]() R.
R.
2
Відповідь: літак повинен летіти зі швидкістю ≈ 460 ![]() м з заходу с
м з заходу с
на схід на екваторі; а на широті 60° зі швидкістю ≈ 230 ![]() м, щоб у с
м, щоб у с
обох випадках пасажирам цього літака Сонце здавалося нерухомим на небі.
Задача 3.
Маховик, що затримується гальмом, за t c повертається на кут ϕ( )t = 4t − 0,3t 2 (радіан). Визначте:
а) кутову швидкість обертання маховика в момент часу t = 2c;
б) в який момент часу маховик перестане обертатись? Розв’язання:
При рівномірному русі по колу
ω=ϕ![]() , при
нерівномірному - t
, при
нерівномірному - t
ω=ϕ′(t).
а) ω= 4 − 0,6t,ϕ′(2) = 4 − 0,6⋅2 = 2,8.
б) припинення обертання маховика відповідає значенню ω= 0,
тобто
4 −
0,6t = 0,
t = 6![]() .
.
Відповідь: кутова швидкість обертання маховика за 2 с
становить2,8 ![]() рад, а перестане маховик
обертатися через 6
рад, а перестане маховик
обертатися через 6 ![]() 2 с. с 3
2 с. с 3
4.ВЕКТОРИ
Всі фізичні величини діляться на скалярні (робота, шлях, час, сила струму, напруга і ін.) і векторні (швидкість, прискорення, переміщення, сила, напруженість електричного поля і ін.).
Розрізняють вільні і зв’язані вектори.
Вільні вектори (швидкість, прискорення і ін.) визначаються лише числовим значенням і напрямом.
Зв’язані вектори (сила і ін.) – числовим значенням, напрямом і точкою прикладання. При паралельному перенесенні зв’язаного вектора отримуємо інший вектор. Зі сказаного випливає, що сили і інші зв’язані вектори можна додавати лише тоді, коли вони прикладені до однієї точки.
Задача 1.
Додайте сили F1 = 3H i F2 = 4H, що утворюють з віссю ОХ кути α=10° i β= 40°. Визначте кут між рівнодійною силою і віссю ОХ
(мал.45, мал.46).
Розв’язання:
![]()
![]() 2 ≈ 6,8;
2 ≈ 6,8;
Відповідь: рівнодійна сила F=6,8 Н, а кут між рівнодійною силою і віссю ОХ становить γ≈ 27°.
Задача 2.
До однієї точки прикладені три рівні за модулем сили. При якій умові одна з цих сил може бути більшою за суму двох інших? Розв’язання:
![]()
![]() Знайдемо умову, при якій
Знайдемо умову, при якій
F3 > F1 + F2
F![]() або
або
F
![]() ,
,
З малюнка 48 маємо α< 240°
Зауваження: Слід звернути увагу на розв’язок тригонометричної нерівності.
Відповідь: одна з сил може бути більшою за суму двох інших при такій умові:120° <α< 240°. Задача 3.
Двоє коней біжать берегами річки і тягнуть масивну баржу паралельно до берегів. Чому дорівнює сила опору води, якщо канати натягнуті силами 600Н і 700Н, а кут між ними дорівнює 60°? Розв’язаня:
![]() З умови задачі ми можемо зробити припущення, що рух рівномірний.
В цьому випадку сила опору води буде дорівнювати рівнодійній сил 600Н і
700Н (мал. 49).
З умови задачі ми можемо зробити припущення, що рух рівномірний.
В цьому випадку сила опору води буде дорівнювати рівнодійній сил 600Н і
700Н (мал. 49).
![]() F
= 6002 + 7002 − 2⋅600⋅700⋅cos120° ≈1127
F
= 6002 + 7002 − 2⋅600⋅700⋅cos120° ≈1127
Відповідь: сила опору води приблизно дорівнює 1127 Н.
Задача 4.
r До точкиr прикладені дві перпендикулярніr одна до одної сили
F1 = 3H i F2 = 4H . Під яким кутом до F2 має бути прикладена сила r r r r r
F3 , щоб F1 + F3 = F2 ? Під яким кутом до F1 має бути прикладена сила r r r r
F3 , щоб F2 + F3 = F1 ?
![]()
![]() Розв’язання: (мал.50,51). Розглядаючи прямокутні трикутники,
з малюнків визначаємо шукані величини:
Розв’язання: (мал.50,51). Розглядаючи прямокутні трикутники,
з малюнків визначаємо шукані величини:
![]()
Відповідь: до F2 F1 має бути прикладена сила F3 під кутом r r
α≈ 37°, а до F1 має бути прикладена сила F3 під кутом β≈ 53°.
III.ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ
1.ПОХІДНА ТА ЇЇ ЗАСТОСУВАННЯ
Похідна як швидкість зміни функції Досить часто учні ототожнюють швидкість зміни функції з механічною швидкістю. Тому при введені поняття похідної доцільно урізноманітнити функції і аргументи.
1.
При рівномірному прямолінійному русі υ=
![]() S , при
S , при
t
нерівномірному русі - υ= S′(t).
2.
При постійному струмі I = ![]() q , при змінному струмі
I = q′(t).
q , при змінному струмі
I = q′(t).
t
3.
При рівномірному русі по колу ω=ϕ![]() , при
нерівномірному - t
, при
нерівномірному - t
ω=ϕ′(t).
4. Розглянемо відому формулу Q = cm∆T (фізика, 8клас), де Q - кількість теплоти, m - маса,
∆T - різниця температур, с – питома теплоємність.
Для m=1кг Q = c∆T . Для змінної температури c = Q′(T).
5.
![]() В шкільному курсі фізики і повсякденному житті розглядається
об’ємна густина, що дорівнює масі одиниці об’єму: ρ= .(ρ—густина,
m—маса, V—об’єм). 6.
Під лінійною густиною мається на увазі маса одиниці
В шкільному курсі фізики і повсякденному житті розглядається
об’ємна густина, що дорівнює масі одиниці об’єму: ρ= .(ρ—густина,
m—маса, V—об’єм). 6.
Під лінійною густиною мається на увазі маса одиниці
довжини: ρl = ![]() m (l − довжина).
m (l − довжина).
t
Розглянемо стержень неоднорідної густини (неоднорідний стержень). Нехай початок координат (мал.52) співпадає з кінцем стержня, а весь стержень лежить вздовж осі 0l.
Середня густина між точками l1 і l2 дорівнює відношенню:
m2 − m1
ρl сер = ![]() , ρl = m′(
)l .
, ρl = m′(
)l .
l2 − l1
Механічний зміст похідної. Похідна у фізиці і техніці
Вивчаючи в курсі початків математичного аналізу тему „Похідна у фізиці й техніці”, учні мають можливість пов’язати матеріал, вивчений ними на уроках фізики і технічних дисциплін, з темою „Похідна”.
Приклад 1.
Знайдіть швидкість і прискорення в момент часу t і в момент, коли t =1c для точки, що рухається прямолінійно за законом:
s t( ) = 2t3 −3 .t (s—шлях у метрах, t—час у секундах).
Розв'язання:
Враховуючи механічний зміст похідної, маємо: v(t)= s′(t)= 6t 2 −3.
Якщо t =1, то v(1) = 6⋅12 −3 = 3(м/с). Аналогічно: a(t)= v′(t)=12t .
Якщо t =1, то a(1) =12⋅1 =12(м/с 2 ). м м
Відповідь: ν= 3 ![]() ; а
=12
; а
=12 ![]() 2 . c с
2 . c с
Приклад 2.
Маховик під дією гальма за час t повертається на кут ψ(t)= 4t − 0,3t 2 . Визначте: 1) кутову швидкість ω(t) обертання маховика в момент часу t = 2c; 2) в який момент маховик перестане обертатися (ψ(t)— кут в радіанах, t— час в секундах).
Розв'язання:
1) Враховуючи механічний зміст похідної, знайдемо спочатку кутову швидкість маховика в момент часу t, а потім при t = 2c:
ω(t)
=ψ′(t)
= 4 − 0,6t; при t
= 2c ω= 4 − 0,6⋅2 = 2,8
![]() рад.
рад.
с
2) Маховик перестане обертатися тоді, коли його швидкість буде дорівнювати 0. Тому прирівняємо до 0 знайдену швидкість обертання маховика в момент часу t і знайдемоt.
4 − 0,6t = 0;
0,6t = 4,
2
t
= 6 ![]() c.
c.
3
рад 2
Відповідь:ω= 2,8 ![]() ; t
= 6
; t
= 6 ![]() c.
с 3
c.
с 3
Приклад 3.
Зміна сили струму I залежно від часу задається рівнянням
I = 2t 2 −5t (I – в амперах, t– в секундах). Знайдіть зміну сили струму в момент t =10c.
Розв’язання:
Враховуючи механічний зміст похідної, знаходимо похідну сили струму, а отже, і швидкість зміни сили струму: I′(t) = 4t −5.
I′(10) = 4⋅10 −5 = 35(А/с).
Відповідь:I′ = 35 ![]() A. c
A. c
Приклад 4.
Відомо, що тіло масою 5 кг рухається прямолінійно за законом s t( ) = t 2 + 2 (s – шлях у метрах, t– час у секундах). Знайдіть кінетичну енергію тіла через 2 с після початку руху.
Розв’язання:
Враховуючи механічний зміст похідної та формулу для обчислення кінетичної енергії тіла, маємо:
v(t) = s′(t) = 2t , v(2)= 2⋅2 = 4(м/с).
E ![]() .
.
м
Відповідь:
ν= 4 ![]() ; Е
= 40 Дж.
; Е
= 40 Дж.
с
Приклад 5.
Тіло масою 2 кг рухається прямолінійно за законом х(t) = t2 + t +1. Координата x вимірюється в сантиметрах, час t – в
секундах. Знайдіть: 1)діючу силу; 2)кінетичну енергію E тіла через 2 с після початку руху.
Розв’язання:
Враховуючи механічний зміст похідної, знаходимо v і a:
v(t)= x′(t)= 2t +1;
a( )t = v′(
)t = 2(![]() см2 ) = 2⋅10−2 (
см2 ) = 2⋅10−2 ( ![]() м2 ). с с
м2 ). с с
За другим законом Ньютона знаходимо силу, що діє на тіло:
F = ma;
F = 2⋅2⋅10−2H = 0,04H.
Кінетична енергія руху тіла обчислюється за формулою:
mv2
E ![]() ;
;
v( )2 = 2⋅2 +1= 5(![]() см) = 5⋅10−2 (
см) = 5⋅10−2 (![]() м). с с
м). с с
Е 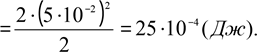
Відповідь: F = 0,04H; E = 25⋅10−4 Дж.
Фізичні задачі на екстремум функції
Задача 1. Рятівник поблизу берега озера повинен надати допомогу людині, яка тоне. Знаючи свою швидкість руху на суші v і у воді u , він повинен вибрати траєкторію, при якій допомога прибуде через мінімальний час. Якій умові повинна відповідати траєкторія?
Розв’язання:
![]() Рятівник біжить швидше ніж пливе. Здається, йому слід бігти
до тієї точки берега, звідки буде коротшим відрізок шляху у воді. Але при цьому
збільшується загальний шлях, а від нього також залежить результат. І мінімальність
часу при такому виборі траєкторії видається також неймовірною. Задамо траєкторію
рятівника двома відрізками
Рятівник біжить швидше ніж пливе. Здається, йому слід бігти
до тієї точки берега, звідки буде коротшим відрізок шляху у воді. Але при цьому
збільшується загальний шлях, а від нього також залежить результат. І мінімальність
часу при такому виборі траєкторії видається також неймовірною. Задамо траєкторію
рятівника двома відрізками
СО – на суші і ОТ – у воді. Проведемо через точку Т перпендикуляр до берега і введемо позначення:
CB = l, AB = h1 , AТ = h2 . З врахуванням заданих швидкостей загальний час руху рятівника:
CO OT
![]() t0 = + чи v u
t0 = + чи v u
![]() x
2 + h12 (l − x)2 +
h22 t0 = + . v u
x
2 + h12 (l − x)2 +
h22 t0 = + . v u
Загальний час визначається вибором точки О чи відрізка x. Про диференціюємо отриману функцію t0 (x) по x і прирівнюючи похідну до нуля, отримаємо:
![]() x l
− x
x l
− x
⋅ − ⋅ = 0.
Врахуємо, що x = sinα і l − x = sinβ.
![]()
![]() (l
− x)2 + h22
(l
− x)2 + h22
Тому умову екстремуму можна записати у вигляді:
sinα sinβ sinα v
![]() =
чи = . v u sinβ
u
=
чи = . v u sinβ
u
Додаткове дослідження показує, що отримана умова екстремуму відповідає мінімуму функції.
Задача 2.
Потрібно перекинути каміння через перешкоду висотою h. Горизонтальна відстань від перешкоди l. При якій мінімальній швидкості каміння це можна виконати?
Розв’язання:
В цій задачі траєкторії польоту каміння параболічні. Вид параболи залежить від величини і напрямку початкової швидкості. Умова задачі виділяє дві точки, через які повинна проходити парабола. Але таких парабол можна провести безліч, змінюючи кут і модуль початкової швидкості, можна отримати множину траєкторій, які проходять через дві задані точки. Із рівнянь для парабол, які проходять через умовні точки, можна виразити початкову швидкість як функцію кута.
![]() Зв’яжемо з точкою вильоту каміння систему координат і конкретизуємо
умову. На каміння діє тільки сила тяжіння, яка надає їм прискорення g, напрямлене
вертикально вниз. Тому зміна їх координат:
Зв’яжемо з точкою вильоту каміння систему координат і конкретизуємо
умову. На каміння діє тільки сила тяжіння, яка надає їм прискорення g, напрямлене
вертикально вниз. Тому зміна їх координат:
x = v0 cosα0t;
gt 2
y = v0 sinα0t − ![]() .
.
2
Виключаючи t, отримаємо рівняння параболи:
x
t = ![]() ; v0 cosα0
; v0 cosα0
gx 2
y ![]() .
.
При
x = l ,
y = h,
тому h ![]() gl 2 .
gl 2 .
gl 2
Звідси v![]() .
.
Оскільки чисельник в заданих умовах не змінюється, можна дослідити на екстремум лише знаменник функції. Перетворимо його:
cos2 α0 (l ⋅tgα0 − h) = l ⋅cosα0 ⋅sinα0 − h⋅cos2 α0 .
Продиференціюємо отримане і прирівняємо до нуля:
l ⋅cos2 α0 −l ⋅sin 2 α0 + 2hcosα0 ⋅sinα0 = 0 .
Отримане рівняння приведемо до вигляду:
2 2h tg α0 − ![]() ⋅tgα0 −1 = 0.
⋅tgα0 −1 = 0.
l
Ввівши позначення tgα0 = x, отримаємо x
2 − ![]() 2h x −1= 0.
2h x −1= 0.
l
Корені рівняння: x1.2 =
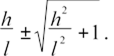
Другий, від’ємний, корінь не відповідає умові задачі, тому
![]()
![]() h
+ h2 + l 2 h
+ h2 + l 2
h
+ h2 + l 2 h
+ h2 + l 2
tgα0 = і α0 = arctg. l l
gl 2
При цьому значенні аргумента функція v![]() набуває
мінімального значення.
набуває
мінімального значення.
Задача 3. На човні необхідно переправитись на протилежний берег швидкої річки, швидкість течії якої u більша, ніж швидкість човна vл. Під яким кутом до течії повинна бути направлена швидкість човна, щоб знесення її течією було мінімальним?
Розв’язання: Швидкість човна відносно берега визначається векторною сумою її швидкості відносно води vл і швидкості течії u . Направимо вісь x за течією, а вісь y впоперек. Позначимо ширину річки через b. Оскільки проекція вектора суми рівна алгебраїчній сумі проекцій додавання векторів, то v0x = vл cosα+ u і voy = vл sinα.
Знесення човна за час руху S = vox ⋅t,
де t = ![]() b . Роблячи vл ⋅sinα
b . Роблячи vл ⋅sinα
підстановку, отримаємо:
S
= (vл cosα+ u)⋅ ![]() b
b
vл sinα
чи
u
S =
bctgα+ ![]() vл sinα.
vл sinα.
Знайдемо значення кута, при якому функція
u
S =
bctgα+ ![]() vл sinα
має екстремум:
vл sinα
має екстремум:
![]() .
.
vл ⋅sin α
vл
Звідки vл + u ⋅cosα= 0, і тоді cosα= − ![]() . u
. u
Кут, під яким слід тримати напрямок, щоб знесення човна
vл течією було мінімальним,
дорівнює α= arccos− ![]() .
.
u
Задача 4.
Санчата з вантажем загальною масою m потрібно здвинути з місця. Коефіцієнт тертя спокою санчат об сніг µ. Яку мінімальну силу треба прикласти для цього?
Розв’язання: Прикладемо всі сили до центра мас системи. Шукану силу можна представити сумою двох компонентів: Fx = F ⋅cosα і
Fy = F ⋅sinα. Тоді умова рівноваги при максимальній силі тертя спокою:
Ox: F ⋅cosα− Fтр.max = 0;
![]() Oy : F ⋅sinα+ N − mg = 0 ⇒
Oy : F ⋅sinα+ N − mg = 0 ⇒
⇒ N = mg − F sinα
Максимальна сила тертя спокою пропорційна силі, яка тисне, рівна по модулю N , тобто
Fтр.max = µ(mg − F sinα). Виходить, що зменшуючи кут α, ми збільшуємо Fx , але при цьому зростає і Fтр.max , яку потрібно компенсувати.
Маємо:
F ⋅cosα−µmg +µF ⋅sinα= 0.
µmg
Звідси F = ![]() .
.
cosα+µ⋅sinα
Оскільки чисельник сталий, дослідимо на екстремум знаменник.
Продиференціюємо знаменник і прирівняємо до нуля, отримаємо:
−sinα+µcosα= 0, звідки α= arctgµ. Тоді екстремум функції
µmg
F = ![]() : cosα+µ⋅sinα
: cosα+µ⋅sinα
µmg
![]() F = . cos(arctgµ)+µsin(arctgµ)
F = . cos(arctgµ)+µsin(arctgµ)
Додаткове дослідження показує, що це мінімум.
Задача 5.
В горизонтальній трубі довжиною l знаходиться позитивно заряджена кулька. Поблизу протилежних кінців труби знаходяться закріплені позитивні заряди q1 і q2 . Знайдіть положення рівноваги кульки із умов мінімальності потенціальної енергії системи в цьому положенні.
Розв’язання:
q1 ⋅qш
Потенціальна енергія кульки в полі заряду q1 : Wп1 = k ⋅ ![]() і в r
і в r
q2 ⋅qш полі заряду q2 : Wп2 = k ⋅ ![]() . l
− r
. l
− r
![]() Сумарна
потенціальна енергія Wн ( )r = k ⋅qш q1 + q2 .
Сумарна
потенціальна енергія Wн ( )r = k ⋅qш q1 + q2 .
r l − r
![]() Екстремум
функції Wн (
)r = k
⋅qш q1 + q2 відповідає умові
Екстремум
функції Wн (
)r = k
⋅qш q1 + q2 відповідає умові
r l − r
рівноваги. Продиференціювавши і прирівнявши похідну до нуля, маємо:
![]() kqш −rq2 1 +
(l
−q2r)2 = 0.
kqш −rq2 1 +
(l
−q2r)2 = 0.
Звернемо увагу на те, що отриманий результат фактично виражає умову компенсації кулонівських сил. Мінімум потенціальної енергії відповідає умові компенсації сил. Ми отримуємо можливість характеризувати умову рівноваги як стан, в якому потенціальна енергія системи мінімальна. Це широко використовувана у фізиці інтерпретація умови рівноваги.
![]()
![]() Із рівності kqш −rq2 1 +
(l
−q2r)2 = 0 слідує: rq12 = (l −q2r)2 .
Із рівності kqш −rq2 1 +
(l
−q2r)2 = 0 слідує: rq12 = (l −q2r)2 .
Звідси
(q1 − q2 )r 2 − 2q1lr + q1l 2 = 0;
![]() 2q1l ± 4q1l 2 − 4l 2q1(q1 − q2 )
r1,2 =.
2q1l ± 4q1l 2 − 4l 2q1(q1 − q2 )
r1,2 =.
2(q1 − q2 )
Перший корінь не відповідає умові, оскільки при r〉l кулька поза трубою. Тому кулька в рівновазі, коли відстань від заряду q1 рівна:
![]() q1 − q1 ⋅q2 r =⋅l.
q1 − q1 ⋅q2 r =⋅l.
q1 − q2
Задача 6.
Два однакових додатних заряди величиною q розміщені на відстані a один від одного. В якій точці на осі симетрії напруженість результуючого поля, створеного цими зарядами, максимальна?
Розв’язання:
![]()
![]() Побудуємо графік і введемо позначення:
Побудуємо графік і введемо позначення:
OA = x;
r =
Напруженість поля, створюваного кожним
зарядом в точці A, рівна
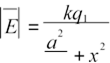 .
Відповідно принципу суперпозиції, загальна
.
Відповідно принципу суперпозиції, загальна
4
![]()
напруженість визначається векторною сумою E0 = E1 + E2 . Модуль
результуючої напруженості, як видно із графіка чи теореми ϕ ϕ x
![]()
![]() косинусів: E0 = 2 E1 ⋅cos
косинусів: E0 = 2 E1 ⋅cos ![]() , і оскільки
cos = ,
то
, і оскільки
cos = ,
то
2 2
E0 ( )x = 2kq1 x 3/ 2 .
![]() a 2 2
+ x
a 2 2
+ x
4
Для знаходження екстремуму отриманої функції продиференціюємо її і прирівняємо похідну до нуля:
a 2 2
![]() 2kq1 − 2x 4
2kq1 − 2x 4
= 0.
a 2 2 5 / 2
+ x
4
Звідси отримаємо: ![]() a 2 −
2x 2 = 0 і x1,2 = ±
a .
Обидва корені
a 2 −
2x 2 = 0 і x1,2 = ±
a .
Обидва корені
4 ![]()
входять в область допустимих значень функції.
16kq1
![]() E0 max =2 . 3 6 ⋅a
E0 max =2 . 3 6 ⋅a
Це значення напруженості буде в точках, симетрично розміщених відносно лінії, яка з’єднує заряди.
Задача 7. При дії на механічну коливальну систему, гармонічно змінюючи внутрішню силу F = F0 ⋅sinωt, в ній встановлюються вимушені коливання з амплітудою:
F0
![]() A
=, m (ω02 −ω2 )2 + 4β2ω2
A
=, m (ω02 −ω2 )2 + 4β2ω2
де m – маса системи, ω0 – власна циклічна частота коливань
системи, β – показник затухання, який характеризує силу опору середовища. При якій частоті ω періодичної внутрішньої сили настане резонанс, тобто амплітуда стане максимальною?
Розв’язання:
Знайдемо частоту, при якій підкореневий вираз знаменника
F0 функції A = досягає екстремуму.
![]() m
(ω02 −ω2 )2 + 4β2ω2
m
(ω02 −ω2 )2 + 4β2ω2
Продиференціювавши його і прирівнявши до нуля, отримаємо:
2(ω02 −ω2 )(− 2ω)+8β2ω= 0;
− 4ω(ω02 −ω2 − 2β2 )= 0;
![]() ω1 = 0; ω2 = ω02 − 2β2 .
ω1 = 0; ω2 = ω02 − 2β2 .
Перший корінь не відповідає умові задачі, тому кінцево:
![]() ωрез. =
ω02 − 2β2 .
ωрез. =
ω02 − 2β2 .
Тоді:
F0
Aрез. = 2 .
![]() 2mβ⋅ ω02 −β
2mβ⋅ ω02 −β
Задача 8.
По похилій площині, яка утворює кут α з горизонтом, втягують за шнурок ящик. Коефіцієнт тертя ящика об площину µ. При якому куті β між шнуром і горизонтом потрібна мінімальна сила для витягування ящика?
Розв’язання: Отримаємо функцію, яка виражає залежність необхідної сили від кута β. Нехай до ящика прикладена сила F під кутом β до горизонту. Направимо координатні осі вздовж похилої площини і перпендикулярно до неї. Тоді умова рівноваги в проекціях: Ox : F cos(β−α)− Fтр. − mgsinα= 0; Oy : F sin(β−α)+ N − mg cosα= 0. Виразимо із Oy : F sin(β−α)+ N − mg cosα= 0 N : N = mg cosα− F sin(β−α), і тоді для сили тертя:
Fтр. = µ(mg cosα− F sin(β−α)). З врахуванням отриманого для сили тертя формула Ox : F cos(β−α)− Fтр. − mgsinα= 0 набуде вигляду: F cos(β−α)−µmg cosα+µF sin(β−α)− mgsinα= 0. Звідси
mg(sinα+µcosα)
![]() F = . cos(β−α)+µsin(β−α)
F = . cos(β−α)+µsin(β−α)
Цю функцію треба дослідити на екстремум, вважаючи змінною (β−α).
Задача 9.
Людина може рухатися по полю з швидкістю v, а по шосе – з швидкістю u . Їй необхідно із точки A в полі потрапити в точку C на шосе. Під яким кутом до шосе їй потрібно рухатися, щоб потрапити в точку C за мінімальний час?
Розв’язання:
![]() Виділимо два відрізки траєкторії
– AB і BC і введемо позначення. Загальний час руху:
Виділимо два відрізки траєкторії
– AB і BC і введемо позначення. Загальний час руху:
AB BC
![]() t0 = + . Використовуючи графік,
v u
t0 = + . Використовуючи графік,
v u
виразимо відрізки AB і BC через h, l і ϕ:
h h AB = ![]() ; BC
= l −
; BC
= l − ![]() . sinϕ tgϕ
. sinϕ tgϕ
Після підстановки при заданих v і u час виражається як функція
![]() кута: t0 = h +
l − h . Цю функцію
потрібно дослідити на vsinϕ u u ⋅tgϕ
кута: t0 = h +
l − h . Цю функцію
потрібно дослідити на vsinϕ u u ⋅tgϕ
екстремум.
Задача 10.
В вертикальній трубі знаходиться стовп рідини висотою H . На якій висоті h від основи слід зробити отвір в стінці труби, щоб дальність польоту струменя виявилась максимальною?
![]()
![]()
![]() x =
v0x ⋅t . Початкова
x =
v0x ⋅t . Початкова
швидкість струменя
2
основі наведених співвідношень для
Задача 11.
Гелій масою m в циліндрі під поршнем займає об’єм V1 при тиску p1. Цей газ повільно переводять в стан з параметрами V2 і p2 , причому процес переходу характеризується законом p = b − a ⋅V . Визначте максимальну температуру в цьому процесі.
Розв’язання:
Макроскопічні параметри стану газу зв’язані рівнянням
m
Менделєєва-Клапейрона: pV = ![]() RT . Тут M
– молярна маса газу,
RT . Тут M
– молярна маса газу,
M
R – універсальна газова стала. Підставимо сюди вираз для p:
m
(b −
aV)⋅V
= ![]() RT . Звідси температура як функція об’єму:
RT . Звідси температура як функція об’єму:
M
T(
)V = ![]() M ⋅(bV
− aV 2 ).
M ⋅(bV
− aV 2 ).
mR
Значення параметрів початкового і кінцевого стану газу дозволяє конкретизувати коефіцієнти a і b.
p1 = b − aV1 ,
p2 = b − aV2 .
Розв’язуючи дану систему, отримаємо:
p1 − p2 p1V2 − p2V1 a = ![]() і b
=
і b
= ![]() .
.
V2 −V1 V2 −V1
І так, слід дослідити на екстремум функцію
T( )V = ![]() M ⋅(bV
− aV 2 )
і використати отримані вирази для mR коефіцієнтів.
M ⋅(bV
− aV 2 )
і використати отримані вирази для mR коефіцієнтів.
Задача 12.
Електрично заряджена частинка з зарядом e і масою m, пролетівши поле конденсатора, вилітає із нього під кутом β до пластини. Напруженість поля всередині конденсатора E , довжина пластини l. Оцініть інтервал значень кінетичної енергії влітаючої частинки, якщо кут α, під яким вона влітає, не реєструється.
Розв’язання:
В електричному полі конденсатора на частинку діє кулонівська сила, яка надає їй прискорення, напрямлена вздовж лінії напруженості. Проекція вектора швидкості на вісь x,
![]()
перпендикулярна вектору E , залишається незмінною. При невизначеному α можливі два випадки: коли кут між напрямками початкової швидкості частинки і вектором напруженості тупий і коли кут між вказаними напрямками гострий.
Розглянемо перший випадок. Оскільки проекція швидкості на вісь x незмінна, то vcosβ= v0 cosα. Для другої проекції швидкості:
vy =
v0 y − ayt. Прискорення за другим
законом Ньютона: ay =
![]() eE , і
eE , і
m
тому vsinβ= v0 sinα− ![]() eE ⋅t. Час польоту частинки
через конденсатор
eE ⋅t. Час польоту частинки
через конденсатор
m
l t = ![]() . Підставимо в попередню
формулу: v0 cosα
. Підставимо в попередню
формулу: v0 cosα
νsinβ=ν0 sinα− ![]() eEl ..
Поділивши νsinβ=ν0 sinα−
eEl ..
Поділивши νsinβ=ν0 sinα− ![]() eEl
eEl
mν0 cosα mν0 cosα
на vcosβ= v0 cosα,
отримаємо: tgβ=
tgα−
![]() 2eEl 2 . Із цієї mv0 cos α
2eEl 2 . Із цієї mv0 cos α
формули, використовуючи
співвідношення ![]() 12 = tg 2α+1 і cos α
12 = tg 2α+1 і cos α
mv 2
Ek = ![]() , виразимо
кінетичну енергію влітаючої частинки: 2
, виразимо
кінетичну енергію влітаючої частинки: 2
eEl tg 2α+1
![]() Ek = ⋅ .
Ek = ⋅ .
2 tgα−tgβ
Отримали функцію, яку треба дослідити на екстремум. Її дослідження дозволяє визначити мінімум, тобто нижню границю, кінетичної енергії влітаючої частинки.
В другому випадку проекція початкової швидкості частинки на вісь y співпадає за напрямком з прискоренням: vy = v0 y + ay ⋅t,
відповідно vsinβ= v0 sinα+ ![]() eE t , і тоді tgβ= tgα+
eE t , і тоді tgβ= tgα+ ![]() eEl , звідки m mv
eEl , звідки m mv![]()
![]() для
кінетичної енергії отримуємо: Ek =
eEl ⋅ tg 2α+1 .
для
кінетичної енергії отримуємо: Ek =
eEl ⋅ tg 2α+1 .
2 tgβ−tgα
Дослідження на екстремум нової залежності дозволить визначити друге граничне значення кінетичної енергії влітаючої частинки.
Про електричний струм, похідну та комплексні числа
Ми вже якось звикли чути і самі говоримо учням, що математика є могутнім засобом дослідження законів та явищ природи і суспільства, одним із основних чинників науково-технічного прогресу. Учні охоче вірять цьому. Проте шкільний курс математики не передбачає побудови цікавих і змістовних моделей, які б підтверджували подібні висловлювання.
Можна, звичайно, не погодитися з цим, оскільки більшість фізичних законів і правил подаються у вигляді математичних співвідношень. Та в процесі вивчення курсу фізики складається враження, що математика є лише мовою, з допомогою якої зручно записувати ці закони. Тому на прикладі елементарної електротехніки спробуємо з’ясувати, як математика може виступати засобом не лише опису явищ, але і їх дослідження, одержання важливих наслідків, відкриття нових закономірностей.
Даний матеріал можна використати під час викладання математики учням старших класів за умови, що вони володіють поняттям похідної функції як швидкості зміни процесу, який описує дана функція. Базові поняття з теорії комплексних чисел, наведені нижче, не виходять за межі програмових.
Комплексне число α в алгебраїчній формі має вигляд
α= a +bi,
де a,b — дійсні числа, i 2 =−1.
![]()
![]() Комплексне число α зображається
точкою на координатній площині з
Комплексне число α зображається
точкою на координатній площині з
координатами (a і b) або вектором 0α з такими самими координатами.
Поряд з алгебраїчною формою числа α вживають тригонометричну форму:
α= r(cosϕ+isinϕ),
![]()
![]() де
а = r, r
= a 2 + b2 , а ϕ
– кут
де
а = r, r
= a 2 + b2 , а ϕ
– кут
нахилу вектора 0α до осі x, причому
b
sinϕ= ![]() ,
,
r
a cosϕ= ![]() .
.
r
![]() Наприклад,
якщо α=1−i 3, то
Наприклад,
якщо α=1−i 3, то
![]() r = 1+3
= 2, cosϕ=
r = 1+3
= 2, cosϕ= ![]() ,
,
sinϕ=
−![]() ,
,
2
звідки одне зі значень аргументу ϕ=−![]() .
.
Тому тригонометрична форма числа 1−i 3 має вигляд
![]() π π 2cos−
π π 2cos− ![]() +isin− ..
+isin− ..
3 3
Аналогічно для β= −1−i маємо:
![]() r
= 2,
r
= 2,
sinϕ= −![]() , ϕ=
, ϕ= ![]() .
.
![]() одне
із значень:
одне
із значень:
cosϕ= −,
тому
![]() 5π 5π β= 2cos
5π 5π β= 2cos ![]() +isin
+isin ![]() .
.
4 4
Тригонометричну форму комплексного числа зручно застосовувати під час множення чисел. Для цього потрібно модулі співмножників перемножити, а аргументи додати.
Наприклад, для наведених раніше α і β маємо:
![]()
11π
11π αβ= 2 2cos
11π
11π αβ= 2 2cos ![]() +isin
+isin ![]() .
.
12 12
Значний ефект досягається під час піднесення комплексного числа до степеня. Так,
![]() β100 = 2сos
β100 = 2сos
![]() 5π+isin
5π+isin ![]() 5π100 =
5π100 =
4 4
![]() = (
2)
cos +isin =
= (
2)
cos +isin =
4 4
Під час ділення комплексних чисел користуються таким правилом: модуль частки двох чисел дорівнює частці від ділення модуля діленого на модуль дільника, а аргумент — різниці аргументів діленого і дільника. 1. Моделювання змінного струму.
Одним із важливих питань, з якими доводиться мати справу у процесі вивчення електрики є питання про характер змінного струму, а точніше — опис найважливіших характеристик змінного струму — ЕРС (напруги) та сили струму. Школярам у таких випадках запропонуємо остаточний результат.
Наприклад, змінний струм синусоїдальний, тобто сила струму I в кожний момент часу t визначається за формулою:
I = Im sin(ωt +ϕi ), (1)
де Im – амплітуда, ω– частота, ϕi – початкова фаза.
Аналогічну формулу маємо для ЕРС:
ξ=ξm sin(ωt +ϕi ). (2)
Проте ці формули легко довести, використовуючи тригонометричні функції, їх похідні і деякі знання про електричний струм та його походження.
Міркування можуть бути такими. Було помічено, що в провіднику, який рухається в магнітному полі, виникає електричний струм. Зокрема, реальним генератором струму є металева рамка АВ, що обертається між полюсами магніту навколо осі OO1.
![]()
Експериментально виявлено, що індукована в рамці ЕРС пропорційна
швидкості зміни магнітного потоку Ф, який пронизує рамку. Але швидкість зміни
величини — це похідна від цієї величини за часом, тобто ми дістаємо відому з електротехніки
формулу: dΦ ξ= − ![]() .
.
dt
Знак мінус у формулі пов'язаний із напрямом електричного струму.
Вважатимемо, що магнітний потік, який виникає внаслідок дії магніту, є однорідним. Його характеризує рівномірність розподілу силових ліній.
![]()
Якщо рамку розміщено під кутом α до положення АВ, тобто вона займає положення A1B1, то
Φ = Φ0 cosα.
Для рамки, що обертається з кутовою швидкістю ω,
α=ωt +ϕ,
де ϕ характеризує положення
рамки в момент часу t = 0.
Отже,
Φ = Φ0 cos(ωt +ϕ), тому
dΦ
ξ= − ![]() = Φ0ωsin(ωt
+ϕ).
= Φ0ωsin(ωt
+ϕ).
dt
Позначивши Φ0ω=ξm , маємо формулу (2) для ЕРС, що генерується
рамкою в магнітному полі.
Зрозуміло, що напруга U на клемах джерела струму може бути описана такою самою формулою (2), як і ЕРС.
Формулу (1) легко довести, виходячи з формули (2) та закону Ома для електричного кола, що містить активний опір R.
![]()
Оскільки U =Um sin(ωt +ϕU ), то:
![]() U
Um sin(ωt
+ϕu )
U
Um sin(ωt
+ϕu )
I = =
R R
Um
= sin(ωt +ϕu )= Im sin(ωt +ϕu ),
R
де Im =
U![]() m .
m .
R
Під час доведення формули (1) для електричного кола змінного струму, який містить конденсатор з електроємністю C , скористаємося тим, що кількість електрики q на пластинах конденсатора визначається за формулою q =U ⋅C , а сила струму —
за формулою I =
![]() dQ.
dQ.
dt
![]()
![]() Далі маємо
Далі маємо
d(CU) m (ωt +ϕu )= I = = CU ωcos
dt
![]() m u π U (ωt
+ϕi ),
m u π U (ωt
+ϕi ),
= CU ωsinωt +ϕ + = sin
2 X C
1
X C = ![]() , де Cω
. ϕi =ϕu +
, де Cω
. ϕi =ϕu +![]()
Звідси, зокрема, бачимо, що в колі змінного
струму з конденсатором фазові значення струму і напруги відрізняються на кут ![]() , а залежність
між струмом і напругою вже відрізняється від
, а залежність
між струмом і напругою вже відрізняється від
«класичного» закону Ома, хоча зовнішня схожість незаперечна (і не тільки зовнішня!). А залежність між амплітудними значеннями струму і напруги повністю збігається з формулою закону Ома:
Um
Im = ![]() .
.
X C
Не випадково величину X C називають ємнісним опором. Аналогічний зв’язок можна отримати і для ланцюгів змінного струму, що містять індуктивність L, спираючись на умову синусоїдальності змінного струму.
![]() Виходитимемо з того, що ЕРС самоіндукції, яка зумовлює зменшення
струму, дорівнює:
Виходитимемо з того, що ЕРС самоіндукції, яка зумовлює зменшення
струму, дорівнює:
d
ξL = −L ![]() (ωt
+ϕi )
і U L = −ξL.
(ωt
+ϕi )
і U L = −ξL.
dt
Тому:
d
U
L = L ![]() (Im sin(ωt
+ϕi ))=
(Im sin(ωt
+ϕi ))=
dt
=ωLIm sinωt
+ϕi +π![]() = X LIm cos(ωt
+ϕi ),
= X LIm cos(ωt
+ϕi ),
2
де X L =ωL– індуктивний опір ланцюга з індуктивністю. І знову для амплітудних значень маємо: Um = X LIm.
Повний опір змінному струму у випадку, коли електричне коло містить активний R, індуктивний X L та ємнісний X C опори, складається із цих величин. Йдеться не про підсумовування, а про обчислення за формулою:
![]() R2 + (X
L − X C )2 ,
R2 + (X
L − X C )2 ,
обґрунтування якої ми не будемо наводити.
Ми дістали найважливіші характеристики ланцюгів змінного струму і співвідношення між ними, які в подальшому використаємо для реалізації ідеї моделювання змінного струму з допомогою комплексних чисел. 2. Додавання гармонічних коливань.
Наступний крок з реалізації цієї ідеї пов'язано з додаванням синусоїдальних струмів. Ця задача цілком природна. Якщо генератор містить кілька рамок, з'єднаних послідовно, то ЕРС генератора знаходиться шляхом підсумовування всіх ЕРС, що індукуються в кожній рамці (цей факт вважатимемо встановленим експериментально). Виникає запитання: чи є сума двох синусоїдальних ЕРС з однаковою циклічною частотою (або однаковою кутовою швидкістю) знову синусоїдальною?
Позитивну відповідь на це запитання дістанемо додаванням синусоїдальних ЕРС (гармонічних коливань): ξ1 =ξm1 sin(ωt +ϕ1) та ξ2 =ξm1 sin(ωt +ϕ2).
Скориставшись формулами тригонометрії, матимемо:
ξ=ξ1 +ξ2 =ξm1 sin(ωt +ϕ1 )+ξm2 sin(ωt +ϕ2 )=
= (ξm1 cosϕ1 +ξm2 cosϕ2 )sinωt + (ξm1 sinϕ1 +ξm2 sinϕ2 )cosωt =
2 2 a b
![]() = asinωt
+bcosωt
= a +b 2 2 sinωt
+ 2 2 cosωt,
= asinωt
+bcosωt
= a +b 2 2 sinωt
+ 2 2 cosωt,
![]() a +b a
+b
a +b a
+b
де
а =ξm1 cosϕ1 +ξm2 cosϕ2 ,
b =ξm sinϕ1 +ξm sinϕ2.
|
Оскільки |
1 2
2 2 a a 2 + = |
2 2 2 2 1
![]()
![]() a +b a +b
a +b a +b
|
то можна ввести заміну: |
|
|
|
a = α |
b |
= α |
![]() cos ,sin .
cos ,sin .
![]() a2 +b2
a2 +b2
Тоді
ξ= a + b sin(ωt +α) =ξm sin(ωt +α).
Тут
ξm2 =ξm21 +ξm22 + 2ξm1ξm2 cos(ϕ1 −ϕ2).
ξm1 cosϕ1 +ξm2 cosϕ2 cosα= ![]() ,
,
ξm
ξm1 sinϕ1 +ξm2 sinϕ2 sinα= ![]() .
.
ξm
Незважаючи навіть на те, що деякі деталі міркувань тут пропущено, розв'язання задачі досить громіздке.
Пошуки раціонального розв'язання змушують звернутися до комплексних чисел. На думку про можливість використання комплексних чисел (або векторів) може навести схожість формул (1), (2) з тригонометричною формою комплексного числа (фактично йдеться про «уявну» частину комплексного числа, записаного в тригонометричній формі). Та й сама механічна процедура генерування синусоїдальної ЕРС нагадує обертання вектора, що виходить з початку координат, і є геометричним аналогом комплексного числа.
Першим кроком у моделюванні змінного струму з допомогою комплексних чисел може бути розв'язування розглянутої задачі на додавання ЕРС. Справа в тому, що дійсний вираз ξm sin(ωt +ϕ)
і комплексний вираз
ξm (cos(ωt +ϕ)+isin(ωt +ϕ))
знаходяться у взаємно однозначній відповідності і визначають
один одного. Зрозуміло, що ця відповідність зберігається під час додавання гармонічних коливань (ЕРС, сили струмів).
Отже, сумі
ξ1 sin(ωt +ϕ1 )+ξ2 sin(ωt +ϕ2 )
відповідає комплексний вираз:
ξ1 (cos(ωt +ϕ1 )+isin(ωt +ϕ1 ))+ξ2 (cos(ωt +ϕ2 )+isin(ωt +ϕ2 ))=
= (ξ1 (cosϕ1 +isinϕ1 )+ξ2 (cosϕ2 +isinϕ2 ))(cosωt +isinωt).
Звідси випливає, що підсумкова ЕРС є синусоїдальною з тією самою частотою ω. Для знаходження її амплітуди та початкової фази необхідно число
ξ1(cosϕ1 +isinϕ1 )+ξ2 (cosϕ2 +isinϕ2 )
записати в тригонометричній формі (тобто знайти його модуль і
аргумент).
За умови фіксованої частоти гармонічному коливанню
Asin(ωt +ϕ) для кожного t можна поставити у відповідність число A(cosϕ+isinϕ) або вектор довжини A, що утворює кут ϕ з віссю x. Ця відповідність зберігається під час додавання коливань і відповідних комплексних чисел (або векторів). Приклад 1.
Нехай електричне коло змінного струму містить два ланцюги, з’єднані паралельно. Струми, що проходять у кожному з ланцюгів, відповідно дорівнюють:
I1(
)t =10sin2t +π![]() ,
,
3
4π
I2 ( )t = 6sin2t + ![]() .
.
3
Загальний струм I t( ) визначають шляхом додавання I1(t) та
I2 (t).Знайдіть I t( ).
Розв’язання:
Гармонічним коливанням I1(t) та I2 (t) ставимо у відповідність комплексні числа
![]()
![]() 1 π π 12 +i 23 = 5+5 3i
1 π π 12 +i 23 = 5+5 3i
![]()
![]() z
=10cos +isin =10
z
=10cos +isin =10
3 3
![]()
![]() 2 4π 4π − 12 −i 23 = −3−3
3i
2 4π 4π − 12 −i 23 = −3−3
3i
![]()
![]() z
= 6cos +isin = 6
z
= 6cos +isin = 6
3 3
|
Додавши їх, маємо: |
π π |
![]() z1 +
z2 =
2 +
2i 3 =
4cos
z1 +
z2 =
2 +
2i 3 =
4cos ![]() +isin
+isin ![]() .
.
3 3
Тому
![]() I t(
)= 4sin2t +π
I t(
)= 4sin2t +π![]() .
.
3
Геометричний розв’язок наведено на малюнку. Використання комплексних чисел особливо раціональне під час додавання великої кількості гармонічних коливань. Приклад 2.
Маємо п'ять джерел струму, з'єднаних послідовно.
Вони відповідно генерують
напруги:
![]() π
π
U 1 =
3 sin
3 t + ![]()
,
,
6
2π
U 2 =
5 sin
3 t + ![]()
,
,
9
5π
U 3 =
6 sin
3 t + ![]()
,
,
18
π
U 4 =
8 sin
3 t + ![]()
,
,
9
4π
U 5 =
10 sin
3 t + ![]() .
.
9
Знайдіть сумарну напругу.
Розв’язання:
Як і в попередньому прикладі, даним напругам ставимо у відповідність комплексні числа:
1 π π (0,866 + 0,5i)≈ 2,60 +1,5i,
![]()
![]() z = 3cos + isin = 3
z = 3cos + isin = 3
6 6
2 2π 2π (0,766 + 0,643i)≈ 3,83+ 3,21i,
![]()
![]() z = 5cos + isin = 5
z = 5cos + isin = 5
9 9
3 5π 5π (0,643+ 0,766i)≈ 3,86 + 4,60i,
![]()
![]() z = 6cos + isin = 6
z = 6cos + isin = 6
18 18
4 π π (0,940 + 0,342i)≈ 7,52 + 2,74i,
![]()
![]() z = 8cos + isin = 8
z = 8cos + isin = 8
9 9
![]() 5 4π 4π (0,174 + 0,985i)≈1,74 + 9,85i.
5 4π 4π (0,174 + 0,985i)≈1,74 + 9,85i.
z =10cos + i =10
9 9
Оскільки для послідовно з'єднаних джерел струму напруги підсумовуються, то слід додати відповідні комплексні числа: z1 + z2 + z3 + z4 + z5 ≈19,51+ 21,64i = 29,1(cos0,84 +isin0,84).
Отже, U1 +U2 +U3 +U4 +U5 ≈ 29,1sin(3t + 0,84). 3. Комплексна модель змінного струму.
Розв'язання у п. 2 окремої задачі з електротехніки з допомогою комплексних чисел «матеріалізувало» ідею про використання комплексної моделі для подальшого аналізу ланцюгів змінного струму. В історичному плані ця ідея з'явилася досить пізно. Можливо, на дослідників впливало традиційне ставлення до комплексних чисел як до «уявних». Але комплексні числа «реальні» такою самою мірою, як і дійсні. І якщо спрацьовує модель фізичного процесу, побудована на їх основі, то така модель можлива. Наведені раніше комплексні характеристики
•
ξ=ξm (cos(ωt +ϕe )+isin(ωt +ϕe )),
•
U =Um (cos(ωt +ϕu )+isin(ωt +ϕu )),
•
I = Im (cos(ωt +ϕi )+isin(ωt +ϕi ))
для ланцюгів змінного струму називають відповідно
комплексними ЕРС, напругою та силою струму (або комплексом ЕРС, напруги та струму). Перетворивши
• •
I = I m (cosϕ1 +isinϕ1 )(cosωt +isinωt).
і позначивши
•
Im (cosϕi +isinϕi )= Im,
маємо
I• = I• m(cosωt +isinωt). Аналогічно,
• •
ξ=ξm (cosωt +isinωt),
• •
U =U m (cosωt +isinωt),
де
• •
ξ=ξm (cosϕe +isinϕe ),
• •
U =U m (cosϕu +isinϕu ).
• • •
Комплексні числа I m ,ξm,U m називають комплексними амплітудами струму, ЕРС і напруги.
Раніше вже йшлося про те, що для ланцюгів змінного струму наявність індуктивності або ємності не дає можливості скористатися законом Ома, який лінійно пов'язує силу струму і напругу. Тут залежність складніша. Проте комплексні сила струму і напруга пов'язані саме лінійною залежністю. Засновник теорії моделювання ланцюгів змінного струму Ч.П.Штейнмець (1865-1923) зіставив з ємністю С комплексне число
1
RC = XCi = − ![]() i,
ωC
i,
ωC
а з індуктивністю L – число
RL = X Li =ωLi,
назвавши їх відповідно комплексними опорами ємності та
індуктивності.
Якщо коло змінного синусоїдального струму частоти містить активний опір, ємність С та індуктивність L, то число
1
![]() Z = R +
RL + RC = R +ωL
− і називають
комплексним
Z = R +
RL + RC = R +ωL
− і називають
комплексним
ωC
• •
опором кола (комплексом опору) та U = Z I .
Зауважимо ще й те, що модуль комплексного числа називається повним опором кола змінного струму:
2 1 2
![]() Z
= R ωL
− .
Z
= R ωL
− .
ωC
Якщо коло не містить ємності та індуктивності, то повний опір
![]() Z дорівнює активному опору R.
Величину X = X
L − X C називають реактивним
опором. Зрозуміло, що активний опір збігається з дійсною, а реактивний опір – з
уявною частиною комплексного опору електричного кола. Приклад 3.
Z дорівнює активному опору R.
Величину X = X
L − X C називають реактивним
опором. Зрозуміло, що активний опір збігається з дійсною, а реактивний опір – з
уявною частиною комплексного опору електричного кола. Приклад 3.
5π
![]() Під дією напруги U = 220sinωt
+ у колі
проходить струм
Під дією напруги U = 220sinωt
+ у колі
проходить струм
18
π
![]() I =10sinωt
− . Знайдіть
активний та реактивний опори.
I =10sinωt
− . Знайдіть
активний та реактивний опори.
18
Розв’язання:
Комплексні напруга і струм мають вигляд:
![]()
![]() U•
= 220cosωt
+ 5π +isinωt
+ 5π,
U•
= 220cosωt
+ 5π +isinωt
+ 5π,
![]()
![]() 18 18 •
π π I =10cosωt
− +isinωt
− .
18 18 •
π π I =10cosωt
− +isinωt
− .
18 18
Тоді
5π 5π
• 220cos +isin
![]() Z = U•
= Um = 18 18
=
Z = U•
= Um = 18 18
=
I Im 10cosπ +isin π .
18 18
π π
![]()
![]() = 22cos +isin =11+11 3i
= 22cos +isin =11+11 3i
![]() 3 3
3 3
Звідси R =11Ом, Х =11 3Ом.
Приклад 4.
Для кола змінного струму відомі сила струму
π
![]() I
= 5 2sinωt
+
I
= 5 2sinωt
+ ![]() ,
,
6
а також опори X L = 70Ом, ХС = 40Ом,R = 30Ом. Знайдіть напругу U на клемах джерела струму в кожний момент часу t.
Розв’язання:
Знайдемо комплексний опір кола:
![]() Z = 30 +
(70− 40)i
= 30(1+i)= 30 2cosπ
Z = 30 +
(70− 40)i
= 30(1+i)= 30 2cosπ![]() +isinπ
+isinπ![]() .
.
4 4
Тоді
• • π π π π
![]()
![]() U
= I Z = 5 2cosωt
+
U
= I Z = 5 2cosωt
+ ![]() + isinωt
+
+ isinωt
+ ![]() ⋅30 2cos
⋅30 2cos ![]() + isin
+ isin ![]() =
=
6 6 4 4
= 300cosωt
+ ![]() 5π + isinωt
+
5π + isinωt
+ ![]() 5π.
5π.
12 12
Тому U = 300sinωt
+ ![]() 5πВ.
5πВ.
12
Хоча ми зробили лише невеликий крок на шляху застосування похідної та комплексних чисел під час моделювання електричного струму і наведені приклади мають ілюстративний характер до отриманих формул та співвідношень, але вже можна побачити перспективи майбутніх досліджень електричних ланцюгів засобами математики.
2.ІНТЕГРАЛ ТА ЙОГО ЗАСТОСУВАННЯ
Похідна і первісна
Розв’язуючи фізичні задачі, часто доводиться в одних випадках за даною функцією знаходити похідну, а в інших—за даною похідною відновлювати функцію, тобто знаходити первісну. Найдоцільніше виробляти навички в двох напрямах. Задача 1.
Колесо обертається так, що кут повороту пропорційний квадрату часу. Перший оберт було зроблено колесом за 8 с. Визначте швидкість колеса через 48 с після початку руху. Розв’язання:
За умовою ϕ= kt 2 , де φ—кут повороту, t—час.
![]() .
.
Кутова швидкість:
![]() ω(
)t =ϕ′( )t = 2kt = 2⋅ 1 t = 1 t;
ω(
)t =ϕ′( )t = 2kt = 2⋅ 1 t = 1 t;
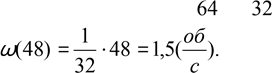
Відповідь: швидкість колеса через 48 с після початку руху
становить 1,5![]() об . с
об . с
Задача 2.
Дощова краплина, початкова маса якої m0, падає під дією сили тяжіння, рівномірно випаровуючись так, що втрата маси пропорційна часу. Через скільки секунд після початку падіння кінетична енергія краплини буде найбільшою?
Розв’язання:
Кінетична енергія обчислюється за формулою:
mυ2
W
= ![]() .
.
2
Через шуканий час t c маса стане дорівнювати m0 − kt, а
(m0 − kt)⋅ g 2t 2 m0 g 2t 2 − kg 2t 3
![]() Wк = = ,
Wк = = ,
2 2
Wк′( )t = ![]() 2m0 g 2t −3kg 2t 2 .
2m0 g 2t −3kg 2t 2 .
2
2m0 g 2t −3kg 2t 2 = 0,
2m0 t = ![]() .
.
3k
Відповідь: через ![]() 2m0 c після початку
падіння кінетична енергія
2m0 c після початку
падіння кінетична енергія
3k
краплини буде найбільшою.
Задача 3.
Матеріальна точка рухається за законом х = 4 + 2t + t 2 (м).
а) Знайдіть швидкість і прискорення. Переконайтесь, що при
заміні початкової координати (4м) на інші її значення, наприклад на 0, 1, 5(м) величина швидкості не зміниться, а при заміні початкової
швидкості (2
![]() м) на 0, 1, 5(
м) на 0, 1, 5( ![]() м ) величина прискорення
не зміниться. с с
м ) величина прискорення
не зміниться. с с
б) За знайденим прискоренням визначте швидкість і координату.
Розв’язання:
а) Розглянемо кожен з заданих випадків: x = 4 + 2t + t 2 ,υ= 2 + 2t. x = 2t + t 2 , υ= 2 + 2t. x =1+ 2t + t 2 ,υ= 2 + 2t.
x = 5 + 2t + t 2 ,υ= 2 + 2t.
υ= 2 + 2t, a = 2. υ= 2 + 2t, a = 2. υ=1+ 2t, a = 2. υ= 5 + 2t, a = 2.
б) а = 2,υ= 2t + C (стала інтегрування—це початкова
швидкість). Для значень початкової
швидкості 0, 1, 5( ![]() м ) с
м ) с
маємоυ= 2t,υ=1+ 2t,υ= 5 + 2t.
Нехай υ= 5 +
2t . Тоді x =
5t + ![]() 2t 2 + C = C + 5t + t 2 , де С—
2t 2 + C = C + 5t + t 2 , де С—
2
початкова координата. Для x0 = 0: x = 2t + t 2 ; для x0 =1: x =1+ 2t + t 2 ; для x0 = 5: x = 5 + 2t + t 2 .
Задача 4.
а) x = 2 + 3t − t 2 + 5t 3 (м)
υ= х′(
)t = 3− 2t +15t 2 ![]() м,
м,
с
а
=υ′(
)t = −2
+ 30t ![]() м2 ; а′(
)t = 30
м2 ; а′(
)t = 30 ![]() м2 .
м2 .
с с
a′(t) - швидкість зміни прискорення.
Рівняння координати виду x = k + k t1 + k2t 2 + k3t 3 відповідає руху зі змінним прискоренням, але при цьому швидкість зміни прискорення є величина стала, тобто a′(t) = const .
б) a′(t) = 30, a = 30t + C, де С—початкове прискорення.
Нехай С = −2 ![]() м2 , тоді а = −2 + 30t,υ= C1 − 2t +15t 2 . с
м2 , тоді а = −2 + 30t,υ= C1 − 2t +15t 2 . с
Нехай C1 = 3 ![]() м , тоді υ= 3− 2t +15t 2 , x = C2 + 3t −t 2 + 5t 3 . с
м , тоді υ= 3− 2t +15t 2 , x = C2 + 3t −t 2 + 5t 3 . с
Нехай C2 = 2м, тоді x = 2 + 3t −t 2 + 5t 3 . Задача 5.
Моторний човен рухається в спокійній воді з швидкістю км
υ0 =
20 ![]() . На повному
ходу її мотор вимикається, і через 40 с після год цього швидкість
човна зменшується до υ1 =
8
. На повному
ходу її мотор вимикається, і через 40 с після год цього швидкість
човна зменшується до υ1 =
8 ![]() км . Опір води прямо
год
км . Опір води прямо
год
пропорційний швидкості руху човна. Визначте швидкість човна через
2 хв. після зупинки мотора.
Розв’язання:
На рухомий човен діє сила опору води:
F = −kυ,
де k〉0 —коефіцієнт пропорційності. З іншої сторони, за другим
законом Ньютона:
F = ma
і, значить,
ma = −kυ чи υ′ = − kν. m
Останнє рівняння—це рівняння виду:
x′ = kx
з початковою
умовою υ0 = 20 ![]() км при t = 0. Тому, згідно з год
км при t = 0. Тому, згідно з год
формулою:
x = Cekt
−![]() kt
kt
маємо: υ= 20e m .
Тепер використовуємо додаткову умову: при t = 40, c = ![]() год,
год,
км
υ=
8 ![]() отримуємо:
отримуємо:
год
![]()
![]() 8 = 20е−mk ⋅901 чи emk = 590.
8 = 20е−mk ⋅901 чи emk = 590.
2
5−90
Тобто υ= 20
![]() .
.
2
Звідси шукана швидкість:
км
![]() км
5−3 км 8
км
5−3 км 8
![]()
![]()
![]() υ= 20 ⋅ = 20 ⋅ = 20 ⋅ = год 2 год 2 год 125
υ= 20 ⋅ = 20 ⋅ = 20 ⋅ = год 2 год 2 год 125
32 км км
= ![]() =1,28
=1,28 ![]() .
.
25 год год
Відповідь: швидкість човна через 2 хв. після зупинки мотора
становить 1,28 ![]() км . год
км . год
Задачі, які допомагають розкрити суть сталої інтегрування Задача 1.
Тіло рухається зі швидкістю υ= 4соs t. За час
t =![]() (c)
воно
(c)
воно
пройшло 20м. Знайдіть рівняння координати.
Розв’язання:
x =
4sint +С.
За умовою 4sin ![]() +C
= 20, C =18.
+C
= 20, C =18.
Відповідь: рівняння координати:x = 4sin t +18 (м).
Задача 2.
Знайдіть кінетичну енергію тіла, яке в момент часу t=4с має
прискорення а = (3t − 2) ![]() м2 , якщо маса тіла дорівнює
5 кг, а с
м2 , якщо маса тіла дорівнює
5 кг, а с
швидкість
при t=0 буде рівною 2 ![]() м. с
м. с
Розв’язання:
mυ2 3t 2
![]() Eк =
Eк = ![]() , C.
, C.
2
За умовою υ(0) = 2 або ![]() .
.
![]() .
.
Ek ![]() .
.
Відповідь: кінетична енергія тіла 490 Дж.
Три задачі з однією математичною моделлю
Задача 1.
Знайдіть площу фігури, обмежену кривою у = 6х − х 2 і віссю абсцис.
Розв’язання:
При х=0 у=0;при у=0 х1=0, х2=6.
S ![]() .
.
Відповідь: площа фігури рівна 36 кв.од.
Задача 2.
Тіло рухається прямолінійно зі швидкістю υ= 6t −t 2 (![]() м). с Знайдіть
довжину шляху, що пройшло тіло від початку руху до зупинки.
м). с Знайдіть
довжину шляху, що пройшло тіло від початку руху до зупинки.
Розв’язання:
При підстановці υ0 = 0 або 6t −t 2 = 0, t1 = 0, t2 = 6.
S ![]() .
.
Відповідь: довжина шляху, що пройшло тіло від початку руху до зупинки становить 36м.
Задача 3.
В колі проходить змінний струм I = 6t −t 2 (A). Знайдіть величину заряду, що пройшов в колі за перші 6с. Розв’язання:
q ![]() .
.
Відповідь: величина заряду, що пройшов в колі за перші 6 с, становить 36 Кл.
Площі, добуток двох величин, сума добутків, інтегральні суми, інтеграл
Задача 1.
Якої величини заряд проходить через провідник, за 5с, якщо: а) сила струму дорівнює 6А;
б) сила струму рівномірно зростає від нуля до 4А;
в) сила струму змінюється за законом
![]() I = t + 2;
I = t + 2;
г) сила струму змінюється за законом
I = t 2 − 2t + 3?
Розв’язання:
а) q = It = 6A⋅5c = 30Кл,
q ![]() .
.
![]()
б) ![]() Кл,
Кл,
q ![]() .
.
![]()
в) ![]() ,5Кл
,5Кл
5 t 2 5
q
= ∫(t
+ 2)dt = ![]() + 2tI0 =
+ 2tI0 =
0 2
![]() ,5(Кл)
,5(Кл)
Знайдемо наближене значення величини заряду як суму площ п’яти прямокутників.
![]() I(0)= 3,
I(0)= 3,
I( )1 = 2,
I( )3 = 6,
I( )4 =11, I( )5 =18.
q ≈ S = 2,5⋅1+ 2,5⋅1+
+ 4,5⋅1+8,5⋅1+
+14,5⋅1= 32,5(Кл)
Знайдемо шуканий заряд з допомогою інтеграла:
q ![]()
![]()
Задача 2.
На матеріальну точку діє сила, яка змінюється обернено пропорційно квадрату відстані до деякого об’єкта. Відомо, що вона складала 1 Н, коли відстань до об’єкта була 2 м. Обчисліть роботу цієї сили по переміщенню матеріальної точки з пункту, що знаходиться на відстані 10 м від об’єкта, до пункту, що знаходиться на відстані 3 м.
Розв’язання:
За умовою F =
![]() k2 ,1=
k2 ,1= ![]() k2 , k = 4.
k2 , k = 4.
S 2
10 4 4S−1 10 4 4 14
![]() A
= ∫
A
= ∫
![]() 2 dS =
2 dS = ![]() ι3 = −
ι3 = − ![]() − (− )
= .
− (− )
= .
3 S −1 10 3 15
Відповідь: робота сили по переміщенню
матеріальної точки з пункту, що знаходиться на відстані 10 м від об’єкта,
до пункту, що знаходиться на відстані 3 м, становить ![]() Дж. Задача
3.
Дж. Задача
3.
Швидкість руху, що пропорційна квадрату часу, в кінці четвертої
секунди дорівнює υ=1
![]() м. Чому дорівнює шлях,
пройдений с
м. Чому дорівнює шлях,
пройдений с
за перші 10 с?
Розв’язання:
1 = k ⋅42 ,
k
![]() . .
. .
S 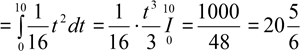 .
.
Відповідь: шлях, пройдений за перші 10 с, становить
20![]() м.
м.
Висновок
Використання фізичного матеріалу сприяє розвитку навичок в застосуванні математичного апарату, дає можливість застосовувати різні методи (векторний, координатний і ін.) для розв’язування прикладних задач, допомагає формувати в учнів уявлення про роль математики у вивченні навколишнього світу, бачити різницю між реальним і ідеальним, між фізичними явищами і математичною моделлю, викликає додатковий інтерес і мотивацію до навчання.
Відібраний для уроків математики фізичний матеріал
має бути простим і, бажано, вже вивченим на уроках фізики.
Список використаної літератури:
1. Бевз В. Міжпредметні зв’язки як необхідний елемент предметної системи навчання // Математика в школі.-2003.-
№6.- с. 6 -11.
2. Білий М.С. Розкриття зв’язків між предметами природничо-математичного циклу // Радянська школа.-1983.№1.-с. 17-24.
3. Бойко Л.М. Реалізація міжпредметних зв’язків математики та фізики в основній школі //
4. Возна М., Гром’як М. Про встановлення взаємоузгодженості програм з математики та суміжних дисциплін // Математика в школі.-2003.-№6.-с.8-11.
5. Гринин А.М. О некоторых приложениях математики к физике // Физика в школе.-1986.-№1.-с.85-86.
6. Далингер В.А. О некоторых приёмах реализации связей “математика-физика” // Физика в школе.-2003.-№3.с.28-34.
7. Донченко М.Т. Про основні напрями взаємозв’язку фізики і математики в середній школі.-З кн. З досвіду навчання фізики в школі.-К.-1980.-с.38-50.
8. Кац М. Физический материал на уроках математики //
Математика.-2001.-№2.-с.15-17.
9. Кац М. Физический материал на уроках математики //
Математика.-2001.-№4.-с.13-16.
10. Кац М. Физический материал на уроках математики
// Математика.-2001.-№5.-с.25-31.
11. Кожекина Т.В. Взаимосвязь обучения физике и математике в одинацатилетней школе // Физика в школе.-
1987.-№5, с.65-68.
12. Некоторые особенности межпредметных связей при изучении физики и математики // Терпилин Н. А. Прикладная направленность школьного курса математики: Книга для учителя. - М.-1990.-Гл.III.-с.82-86.
13. Орлянський О. Три півкола і три параболи // Світ фізики.-2001.-№4.-с.45-50.
14. Пойа Д. Математика и правдоподобные рассуждения М.: Издательство школьной литературы.-1957.
15. Програма з математики для 5-11 класів загальноосвітньої школи / Міністерство освіти і науки
України.-К.-2001.
16. Програма з фізики для 7-11 класів загальноосвітньої школи / Міністерство освіти і науки України.-К.-2001.
17. Старова О.О. Реалізація міжпредметних зв’язків на уроках математики // Математика.-2004.-№3.-с.16-17.
18. Суходольская Н.И. “Веер” межпредметных связей на уроках физики // Физика в школе.-2003.-№3.-с34-35.
19. Томашев Б.И. Некоторые вопросы связи между школьным курсом физики и математики // Физика в школе.-
1980.-№2.-с. 54-56.
20. Фізика і математика // Бугайов О.І. та ін. Фізика.
Астрономія: пробний підручник для 7класу.-К.:Освіта.-1999.с.18-22.
21. Физический материал на уроках математики //
Математика.-2001.-№5.-с.25-31.
22. Хомутский В.Д. Формирование у учащихся понятия о функциональной зависимости величин при осуществлении межпредметных связей математики и физики В кн.: Межпредметные связи естествено-математических дисциплин. - М.-1980.-с83-94.
23. Цатурян А.М. Повторение курса физики с привлечением знаний учащихся по математике // Физика в школе.-1987.- №5.- с. 65–68.
24. Ядренко В.М. Фізика допомагає математиці // У світі математики.-2000.т.6.в.3.-с.45-47.
25. Соколович Ю.А., Богданова Г.С. Фізика—Харків
2002
26. Іванов О.С. Задачі з фізики в середній школі—
К.1971
27. Ірліна М.Є., Савченко Н.О. Збірник задач з фізики—К.1973
Зміст
|
ВСТУП |
|
|
I. АЛГЕБРА |
|
|
1.Пряма та обернена пропорційні залежності |
|
|
2.Задачі на найбільше і найменше значення |
|
|
3.Розв’язування сюжетних задач методом рівнянь |
|
|
II. ГЕОМЕТРІЯ |
|
|
1.Подібність трикутників |
|
|
2.Площі многокутників |
|
|
3.Переміщення та його властивості |
|
|
4.Вектори |
|
|
III. ЕЛЕМЕНТИ МАТЕМАТИЧНОГО АНАЛІЗУ |
|
|
1.Похідна та її застосування |
|
|
2.Інтеграл та його застосування |
|
|
ВИСНОВОК |
|
|
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ |
|

про публікацію авторської розробки
Додати розробку