Задачі з астрономії (частина V)
Про матеріал
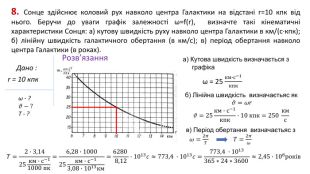
Подані зразки розв'язування задач (частина V) з астрономії, що допомагають перевірити набуті знання учнів та закріпити їхні практичні навички. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дуже вдала презентація. Дякую!
pptx
До підручника
Астрономія (рівень стандарту) 11 клас (Головко М.В., Коваль В.С., Крячко І.П.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку