Задачі "Застосування графічного методу до розв'язування задач з параметром""

-


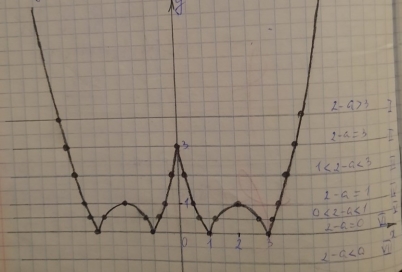 Скільки спільних точок мають графіки заданих функцій у=|x2-4|x|+3|+a та у=2 залежно від параметра а?
Скільки спільних точок мають графіки заданих функцій у=|x2-4|x|+3|+a та у=2 залежно від параметра а?
Розв’язання
Точки перетину заданих графіків функцій співпадають з точками перетину графіків у=|x2-4|x|+3| та у=2-а
у=x2-4x+3=(х-2)2-1 у=x2-4|x|+3 у=|x2-4|x|+3|
І. 2-а>3, a<-1, то дві точки перетину.
ІІ. 2-а=3, а=-1, то три точки перетину
ІІІ.1<2-а<3, -1<а<1, то чотири точки перетину.
ІV. 2-а=1, a=1, то шість точок перетину.
V. 0<2-а<1, 1<a<2, то вісім точок перетину.
VI. 2-а=0, a=2, то чотири точки перетину.
VII. 2-а<0, a>2, точок перетину немає
Відповідь: якщо 2-а>3, a<-1, то дві точки перетину;
якщо 2-а=3, а=-1, то три точки перетину;
якщо 1<2-а<3, -1<а<1, то чотири точки перетину;
якщо 2-а=1, a=1, то шість точок перетину;
якщо 0<2-а<1, 1<a<2, то вісім точок перетин;
якщо 2-а=0, a=2, то чотири точки перетину;
якщо 2-а<0, a>2, точок перетину немає. -


 Скільки спільних точок мають графіки заданих функцій у=||x+2|-1|, y=|x-a| залежно від параметра а?
Скільки спільних точок мають графіки заданих функцій у=||x+2|-1|, y=|x-a| залежно від параметра а?
Розв’язання
y=x+2 y=|x+2| y=|x+2| -1 y=||x+2| -1||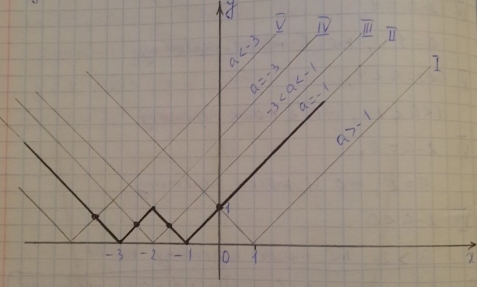
І. а>1, то одна спільна точка.
ІІ. а=-1, то безліч спільних точок.
ІІІ. -3<а<-1, то дві спільні точки.
ІV. a=-3, то безліч спільних точок.
V. a<-3, то одна спільна точка.
Відповідь: якщо ає(-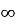 ;-3)
;-3)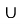 (-1;+
(-1;+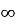 ) то одна спільна точка;
) то одна спільна точка;
якщо ає{-3;-1}, то безліч спільних точок;
якщо ає(-3;-1), то дві спільні точки.
-



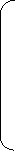
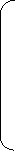 Скільки спільних точок мають графіки заданих функцій у=|x+5|-|4-x|+a, y=1 залежно від параметра а?
Скільки спільних точок мають графіки заданих функцій у=|x+5|-|4-x|+a, y=1 залежно від параметра а?
Розв’язання
Точки перетину заданих графіків функцій співпадають з точками перетину графіків у=|x+5|-|4-x| та у=1-а.
у=|x+5|-|4-x|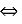 у=|x+5|-|x-4|.
у=|x+5|-|x-4|.
x-4 - - +
x+5 - + +
-5 4
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
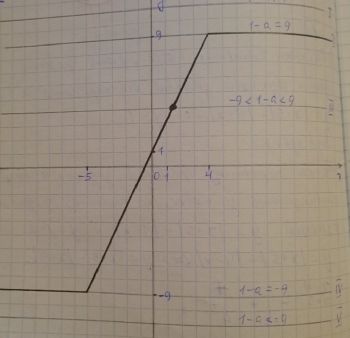
І. 1- а>9, а<8, то спільних точок немає.
ІІ. 1- а=9, а=-8, то безліч спільних точок.
ІІІ. -9<1-а<9, -8< а<10,то одна спільна точка.
ІV. 1- а=-9 a=10, то безліч спільних точок.
V. 1- а<-9, a>10, то спільних точок немає.
Відповідь: якщо ає(-![]() ;-8)
;-8)![]() (10;+
(10;+![]() ) то спільних точок немає;
) то спільних точок немає;
якщо ає{-8;10}, то безліч спільних точок;
якщо ає(-8;10), то одна спільна точка.
-



 Скільки спільних точок мають графіки заданих функцій у=|x+2|+|x-3|, y=а-2х залежно від параметра а?
Скільки спільних точок мають графіки заданих функцій у=|x+2|+|x-3|, y=а-2х залежно від параметра а?
Розв’язання
x-3 - - +
x+2 - + +
-2 3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
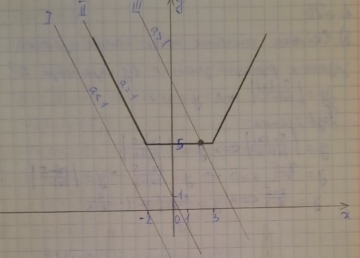
І. а<1, то спільних точок немає.
ІІ. а=1, то безліч спільних точок.
ІІІ. а>1, то одна спільна точка.
Відповідь: якщо ає(-![]() ;1) , то спільних точок немає;
;1) , то спільних точок немає;
якщо а=1, то безліч спільних точок;
якщо ає(1;![]() ), то одна спільна точка.
), то одна спільна точка.
-


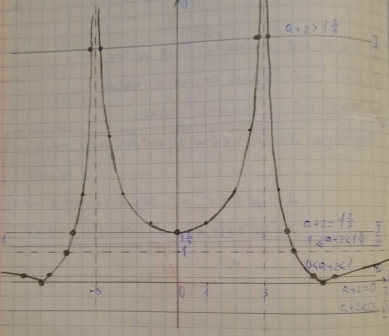 Скільки спільних точок мають графіки заданих функцій у=
Скільки спільних точок мають графіки заданих функцій у=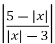 , y=а+2 залежно від параметра а?
, y=а+2 залежно від параметра а?
Розв’язання
у=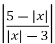
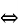 у=
у=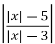
y=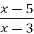 , x
, x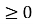 y=
y=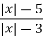 у=
у=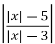 .
.
y=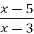 , y=
, y=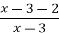 , y=
, y=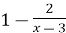 .
.
І. а+2>1![]() , a>-
, a>-![]() , то чотири спільні точки .
, то чотири спільні точки .
ІІ. а+2=1![]() , а=-
, а=-![]() , то три спільні точки.
, то три спільні точки.
ІІІ.1![]() а+2<1
а+2<1![]() , -1
, -1![]() а<-
а<-![]() ,, то дві спільні точки .
,, то дві спільні точки .
ІV. 0<а+2<1, -2<а<-1, то чотири спільні точки.
V. а+2=0, a=-2, то дві спільні точки .
VI. а<-2, то спільних точок немає.
Відповідь: якщо ає(-![]() ;-2), то спільних точок немає;
;-2), то спільних точок немає;
якщо ає{-2}![]() [-1;-
[-1;-![]() ) , то дві спільні точки;
) , то дві спільні точки;
якщо ає(-2; -1)![]() (-
(-![]() +
+![]() ) , то чотири спільні точки. ;
) , то чотири спільні точки. ;
якщо а=-![]() , то три спільні точки.
, то три спільні точки.
-
Скільки спільних точок мають множини А1={(x,y): x, yєR,
|y-x|+|x+y|=2a}, A2={(x,y): x, yєR, x2+y2=1} залежно від параметра а?
Розв’язання.
|y-x|+|x+y|=2a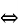
![]()

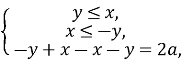
![]()
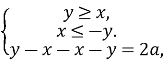
![]()
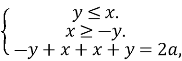
![]()
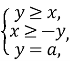
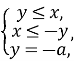
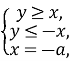
![]()
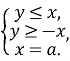
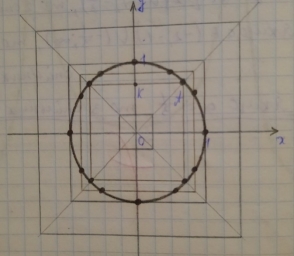
ОА=R=1, R=![]() ; a – сторона квадрата. а=R
; a – сторона квадрата. а=R![]() =
=![]() , OK=
, OK=![]() =
=![]() .
.
Змінюючи сторону квадрата, маємо основні випадки взаємного розміщення множин. х2+у2 – фіксована множина.
І. а >1, то спільних точок немає.
ІІ. а=1, то чотири спільні точки.
ІІІ. ![]() <a<1, то вісім спільних точок.
<a<1, то вісім спільних точок.
ІV. a=![]() , то чотири спільні точки.
, то чотири спільні точки.
V. a<![]() , то спільних точок немає.
, то спільних точок немає.
Відповідь: якщо ає(-![]() ;
;![]() )
)![]() (1;+
(1;+![]() ) , то спільних точок немає;
) , то спільних точок немає;
якщо ає{![]() 1}, то чотири спільні точки;
1}, то чотири спільні точки;
якщо ає(![]() ), то вісім спільних точок.
), то вісім спільних точок.


про публікацію авторської розробки
Додати розробку
