Конспект уроку з алгебри і початків аналізу для 10 класу не тему "Синус, косинус, тангенс кута"

 

Урок№2

Тема уроку: Синус, косинус, тангенс, котангенс кута. Тригонометричні функції числового аргументу.

Мета уроку: сформувати поняття синуса, косинуса, тангенса, котангенса кута, тригонометричних функцiй числового аргумента; домогтися засвоєння учнями значень тригонометричних функцiй окремих чисел та знакiв синуса, косинуса, тангенса i котангенса в кожнiй iз координатних чвертей.

Формування поняття тригонометричних функцій числового аргументу; вивчення значень тригонометричних функцій деяких чисел (кутів), зміни знаків тригонометричних функцій у координатних чвертях.

Сприяти розвитку логічного мислення, просторових уявлень.

Формувати вміння висловлювати думки ясно і вичерпно; виховувати навички охайного і грамотного виконання математичних записів.

Сформувати вміння:

обчислювати значення тригонометричних функцій при окремих значеннях аргументу;

визначати знаки тригонометричних функцій у кожній з координатних чвертей.

Наочність та обладнання:

 конспект «Означення тригонометричних функцій».

Хід уроку

І. Органiзацiйний етап

ІІ. Перевірка домашнього завдання

Математичний диктант

Вставте замість крапок пропущені слова в речення.

1. Якщо , то кут є кутом… чверті.

2. Якщо , то кут є кутом… чверті.

3. Якщо , то кут є кутом… чверті.

4. Якщо , то кут є кутом… чверті.

5. Якщо градусна мiра кута дорiвнює 60° [90°], то його радiанна мiра дорiвнює…

6. Якщо градусна мiра кута дорiвнює 270° [45°], то його радiанна мiра дорiвнює…

7. Якщо радiанна мiра кута дорiвнює , то його градусна мiра дорiвнює…

8. Якщо радiанна мiра кута дорiвнює , то його градусна мiра дорiвнює…

9. Якщо радiанна мiра кута дорiвнює , то його градусна мiра дорiвнює…

ІІІ. Формулювання мети i завдань уроку

Із курсу геометрiї вам вже вiдомi означення синуса, косинуса i тангенса гострого кута прямокутного трикутника, а також означення синуса, косинуса i тангенса кутiв вiд до. У курсi геометрiї було також обґрунтовано, що синус i косинус гострого кута залежать тiльки вiд величини кута i не залежать вiд довжин сторiн трикутника та його розташування, тобто синус i косинус (а отже, i тангенс, i котангенс) є функцiями кута. Пiсля введення поняття кута повороту, величина якого може виражатися будь–яким числом вiд до ,з’явилася можливiсть сформулювати означення тригонометричних функцiй довiльного кута, а з уведенням поняття радiана — означення тригонометричних функцiй числового аргумента. Це i є основне завдання уроку.

ІV. Актуалiзацiя опорних знань

Фронтальне опитування

1. Сформулюйте означення:

синуса гострого кута прямокутного трикутника;

косинуса гострого кута прямокутного трикутника;

тангенса гострого кута прямокутного трикутника.

2. Сформулюйте означення тригонометричних функцiй для кутiв від до.

V. Засвоєння знань

План вивчення теми

1. Означення синуса, косинуса, тангенса, котангенса кута.

2. Означення тригонометричних функцiй числового аргумента.

3. Значення тригонометричних функцiй окремих кутiв.

4. Знаки тригонометричних функцiй у кожнiй iз координатних чвертей.

Конспект учня 21

Означення тригонометричних функцiй

1. Вiзьмемо коло радiуса R iз центром у початку координат (див. рисунок).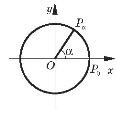

Нехай OP₀ — початковий радiус, — кут повороту радiуса на кут , точка має координати . Тодi:

Синусом кута називається вiдношення ординати точки кола до його радiуса: ;

косинусом кута називається вiдношення абсциси точки кола до його радiуса: ;

тангенсом кута називається вiдношення ординати точки кола до її абсциси: , ;

котангенсом кута називається вiдношення абсциси точки кола до її ординати: , .

Значення, , , залежать тiльки вiд мiри кута i не залежать вiд R.

Зауваження. Якщо вибрати коло радiуса iз центром у початку координат (одиничне коло), то означення тригонометричних функцiй значно спростяться.

Нехай у результатi повороту на кут точка ; переходить у точку . Тодi:

синусом кута називається ордината точки одиничного кола:

косинусом кута називається абсциса точки ;

тангенсом кута називається вiдношення ординати одиничного кола точки одиничного кола до її абсциси: ;

котангенсом кута називається вiдношення абсциси точки одиничного кола до її ординати: .

2. Тригонометричнi функцiї числа — це тригонометричнi функцiї кута в радiан.

Оскiльки значення синуса — це ординати, а значення косинуса — абсциси вiдповiдних точок одиничного кола, причому абсциси й ординати можна знайти для будь–якої точки одиничного кола, то областi визначення функцiй і — усi дiйснi числа. Тобто , .

Для точок одиничного кола абсциси й ординати набувають усiх значень вiд –1 до 1. Отже, множини значень функцiй , — . Тобто ; .

До областi визначення функцiї входять усi дiйснi числа, крiм тих, для яких косинус дорiвнює нулю.

До областi визначення функцiї входять усi дiйснi числа, крiм тих, для яких синус дорiвнює нулю.

Множина значень функцiй — усi дiйснi числа.

4. Значення тригонометричних функцiй окремих кутiв.

	градуси
	радiани
		0				1	0	-1	0
		1				0	-1	0	1
		0		1		не iснує	0	не iснує	0
		не iснує		1		0	не iснує	0	не iснує

 

5. Знаки тригонометричних функцiй

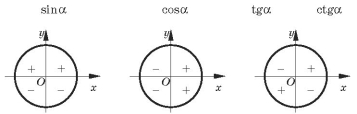
Матерiал цього уроку, що пiдлягає запам’ятовуванню, досить великий за обсягом, тому вчителю необхiдно домогтися розумiння учнями, що — це ордината вiдповiдної точки одиничного кола, а — абсциса.

VІ. Формування вмiнь

Виконання усних вправ

1. Синус якого числа на вiдрiзку дорiвнює:

а) 0; б) 1; в) ; г) ?

2. Косинус якого кута вiдрiзка дорiвнює:

а) 0; б) 1; в) ; г) ?

3. Укажiть декiлька значень , при яких:

а) ; б) ; в) ; г) ; д) ; е) не існує.

4. Чи iснує число , для якого:

а) ; б) ; в) ; г) ; д) ; е) ?

5. Який знак має:

а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) ;

6. Чи правильна нерiвнiсть?

а) ; б) ;

в) ; г) .

Запропонованi вправи призначенi для засвоєння поняття тригонометричних функцiй кута та числового аргумента, запам’ятовування значень тригонометричних функцiй окремих кутiв, формування вмiння визначати знаки тригонометричних функцiй. Крiм того, вони сприяють подальшому формуванню та удосконаленню обчислювальних навичок.

VІІ. Пiдсумки уроку

Контрольнi запитання

1. Сформулюйте означення синуса, косинуса, тангенса та котангенса кута; тригонометричних функцiй числового аргумента.

2. Укажiть область визначення та множину значень функцiй

, , , .

3. Чи iснує таке число, для якого синус i косинус одночасно набувaють: а) рiвних значень; б) значень, якi дорiвнюють нулю?

4. При яких значеннях :

а) дорiвнює нулю, одиницi; б) дорiвнює нулю, одиницi?

5. Для кутiв якої чвертi координатної площини:

а) i мають однаковi знаки;

б) і мають рiзнi знаки;

в) i мають однаковi знаки?

6. Чи може синус вiд’ємного кута набувати додатних значень? Наведiть приклад.

VІІІ. Домашнє завдання

Вивчити означення тригонометричних функцiй, значення тригонометричних функцiй окремих кутiв, знаки тригонометричних функцiй.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Конспект учня

Означення тригонометричних функцiй

1. Вiзьмемо коло радiуса R iз центром у початку координат (див. рисунок).

Нехай OP₀ — початковий радiус, — кут повороту радiуса на кут , точка має координати . Тодi:

Значення, , , залежать тiльки вiд мiри кута i не залежать вiд R.

Синусом кута називається ордината точки одиничного кола:

косинусом кута називається абсциса точки ;

тангенсом кута називається вiдношення ординати одиничного кола точки одиничного кола до її абсциси: ;

котангенсом кута називається вiдношення абсциси точки одиничного кола до її ординати: .

2. Тригонометричнi функцiї числа — це тригонометричнi функцiї кута в радiан.

Оскiльки значення синуса — це ординати, а значення косинуса — абсциси вiдповiдних точок одиничного кола, причому абсциси й ординати можна знайти для будь–якої точки одиничного кола, то областi визначення функцiй і — усi дiйснi числа. Тобто , .

Для точок одиничного кола абсциси й ординати набувають усiх значень вiд –1 до 1. Отже, множини значень функцiй , — . Тобто ; .

До областi визначення функцiї входять усi дiйснi числа, крiм тих, для яких косинус дорiвнює нулю.

До областi визначення функцiї входять усi дiйснi числа, крiм тих, для яких синус дорiвнює нулю.

Множина значень функцiй — усi дiйснi числа.

3. Значення тригонометричних функцiй окремих кутiв.

	градуси
	радiани
		0				1	0	-1	0
		1				0	-1	0	1
		0		1		не iснує	0	не iснує	0
		не iснує		1		0	не iснує	0	не iснує

 

4. Знаки тригонометричних функцiй