Заняття на тему "Застосування логарифмічної функції"

Про матеріал

Наведена розробка теми "Застосування логарифмічної функції" надає можливість відпрацюванню у студентів навичок застосування властивостей логарифмічних рівнянь та нерівностей, показує варіант вивчення теми із застосуванням групової роботи на занятті.

Перегляд файлу

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ДЗЕРЖИНСЬКИЙ ГІРНИЧИЙ ТЕХНІКУМ

МЕТОДИЧНА РОЗРОБКА

відкритого заняття з дисципліни “Математика”

на тему: «Розв'язування вправ. Застосування логарифмічної функції»

спеціальність 5.05030103 Експлуатація та ремонт гірничого

електромеханічного обладнання та автоматичних пристроїв

2012

Методична розробка відкритого заняття з дисципліни «Математика» для студентів І курсу спеціальності 5.05030103 Експлуатація та ремонт гірничого електромеханічного обладнання та автоматичних пристроїв

Підготував: Козлова Г.В. – спеціаліст вищої категорії, викладач-методист Дзержинського гірничого технікуму, Дзержинськ, 2012

Методичну розробку створено на основі наказу № 161 „Про затвердження Положення про організацію навчального процесу у вищих навчальних закладах”

Для викладачів математики, студентів

Рецензенти: А.В. Арчаков, голова методичного об’єднання викладачів математики, спеціаліст вищої категорії Єнакіївського металургійного технікуму

Розглянено та ухвалено на засіданні циклової комісії природничо-математичних дисциплін Дзержинського гірничого технікуму

Протокол № ____ від __________ 2012 року

Голова циклової комісії

____________Г.В.Козлова

Зміст

1.	План відкритого заняття	4
2.	Хід та зміст заняття	6
2.1.	Організація заняття	6
2.2.	Формулювання мети й завдань заняття	6
2.3.	Повторення основних теоретичних та практичних знань	6
2.4.	Застосування практичних знань в стандартних умовах	7
2.5.	Застосування практичних знань в більш складних умовах	8
2.6.	Виконання самостійної роботи	9
2.7.	Підсумок заняття	9
2.8.	Повідомлення домашнього заняття	9
Додаток А. Критерії оцінювання		10

План відкритого заняття

Дисципліна: Математика

Викладач: Козлова Галина Василівна

Дата проведення: 04.12.12

Час проведення: 80 хвилин (І пара: 8.00)

Група: ЕО-12

Кількість студентів: 25

Місце проведення: ауд.№ 28

Тема: Розв'язування вправ. Застосування логарифмічної функції

Мета:

дидактична: узагальнення та систематизація знань студентів з основних термінів, означень та властивостей логарифма та логарифмічної функції; перевірка вмінь студентів: 1) будувати графіки логарифмічних функцій; 2) виконувати перетворення виразів, що містять логарифми; 3) розв’язувати логарифмічні рівняння та нерівності; 4) аналізувати, співставляти, виділяти головне; розвивати інтерес студентів до даної теми шляхом складання нестандартних ситуацій, використання ІКТ та міні-підручника;

виховна: формувати математичну культуру, навички виступу перед аудиторією, розвивати волю (прагнення переборювати труднощі), пам’ять; виховувати вміння працювати в парі;

методична: удосконалення методики проведення практичних занять.

Вид заняття: практичне

Тип заняття: заняття узагальнення та систематизації знань

Методичне забезпечення:

ОК „Логарифми та їх властивості”, «Логарифмічна функція та її властивості»,
картки с завданням роботи на занятті,
міні-підручник,
таблиця «Логарифмічна функція».

Технічні засоби навчання:

Персональний комп’ютер, програма GRAN 1W
Презентація заняття

Міждисциплінарні зв’язки:

Забезпечуючі: «Українська мова (за профспрямуванням)», «Інформатика»

Забезпечуємі: «Обчислювальна техніка та програмування», «Загальна електротехніка», «Електротехніка та електроніка», «Основи гідравліки»

Література

Основна:

1. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенько А.К. Математика. Підручник. К., Вища школа, 2001.

2. Афанасьєва О.М., Бродський Я.С., Павлов О.Л., Сліпенко А.К. Дидактичні матеріали з математики. К., Вища школа, 2001.

3. Лейфура В.М. та ін. Математика: Підручник для студентів екон. спеціальностей вищ.навч.закладів І-ІІ рівнів акредитації/В.М.Лейфура, Г.Г. Голодницький, Й.І.Файст; За ред. В.М.Лейфури. - К.Техніка, 2003

Додаткова

1. Богомолов II.В. Практические занятия по математике. М,: Высш. шк., 1979, 1983, 1990.

2. Савенко Т.П., Паньков В.Г., Попов Ю.Н. Задачи по алгебре и началам анализа. Часть І / Под ред. И.М. Конета. – Каменец – Подольский: Абетка-НОВА, 2004

3. Сборник заданий для государственной итоговой аттестации по математике. Алгебра и начала анализа. 11 класс. Под ред. З.И. Слепкань. – Харьков, “Гимназия”, 2007

Хід і зміст заняття
1. Організаційна частина: 2хв.

Привітання зі студентами;

Відмітка і журналі відсутніх

Перевірка готовності до заняття студентів, аудиторії

2.2. Формулювання мети й завдань заняття 3 хв.

Сьогодні ми проводимо незвичайне заняття і тема його незвичайна - «Логарифмічна рапсодія». Давайте перетворимо наше заняття у невеличке свято – свято логарифмів. Ще Аристотель говорив, що визначення того або іншого поняття, ще не доводить його існування. Отже, доведемо, що логарифмічна функція існує і що дана тема не тільки одна з найважливіших тем математики, а одна з найцікавіших. Не бійтесь складного і невідомого, так як все складне утворюється з найпростішого. Навіщо були придумані логарифми? Звичайно, для прискорення та спрощення виразів. Винахідник перших логарифмічних таблиць Д.Непер говорив: «Я намагався, як тільки міг, відійти від труднощів та нудьги у розрахунках, що так відлякує багатьох від вивчення математики». Дійсно, логарифми набагато швидше прискорюють розрахунки, не говорячи про те, що вони дають можливість робити такі перетворення , виконання яких без допомоги логарифмів є складним (знаходження кореня будь-якого степеня ).

Сьогодні ми працюємо у трьох групах (варіантах), завдання диференційовані, кожна група має по 1-2 консультанта. Консультанти протягом заняття уважно слідкують за відповідями студентів, відмічають їх правильність, проводять корекцію. Всі приклади, що виконуються на занятті біля дошки, ви виконуєте в міні – підручнику.

Отже, почнімо заняття.

2.3. Повторення основних теоретичних та практичних знань 10 хв.

«Розминка». Повторення основних властивостей логарифма шляхом усного розв’язання вправ.

Усно: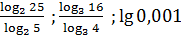;-; ₃; ; ;; + ;; ;

; ; ;

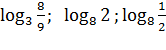Які правила необхідно знати для виконання даних вправ? Студенти дають визначення логарифма, логарифмічної функції, основної логарифмічної тотожності, властивостей логарифма та порівнюють дану функцію із показниковою (слайди № 6,№7)

2.4. Застосування практичних знань в стандартних умовах 25 хв.

І етап. Робота з міні-підручником (вимоги до оцінювання роботи у Додатоку А)

Завдання №1«Перевір себе»

І варіант	ІІ варіант	ІІІ варіант
а)log₅25=	а)log₄64=	а)5 ²⁺^log₅²₌
b)	b)=	b)=
в)log₂18 - log₂9 =	в)log₂11 - log₂44 =	в)log_0,39 – 2log_0,310 =
г) lg20 + lg5 =	г) lg8 + lg125 =	г)3lg2 +0,5 lg25-2 lg2=
д) =	д) ₌	д)lgtgα + lgctgα =

Завдання №2.«Впізнай графік» Вказати для кожної функції відповідний графік.

Перед наступним завдання на побудову графіків функцій студенти спочатку розглядають побудову графіків функцій y=2^-^ІxІ^,y=lgx².(слайди № 8, №9)

Завдання №3. Побудувати графіки функцій

Студенти виконують побудову в міні-підручнику і перевіряють отримані результати у вигляді зображення на ПК за допомогою програми GRAN 1W

1 варіант: у=2^х + log_x₊₃1; 2 варіант: ; у= log₍_x₊₁₎²(x+1)⁴;

3 варіант : у= ;

2.5. Застосування практичних знань в більш складних умовах 10 хв.

Завдання №4

«Знайди помилку» (студенти шукають помилку у даному завданні та пропонують вірне рішення).

1 варіант:

log₀_,5( х-1) >-2

2 варіант:

log₈( х²-4х+3) ≤1

3 варіант:

≥0

х-1>0,5^-2,

х-1>0;

х-5>0,

х-1>0;

х>1

х>5

х є(5;∞)

х²-4х+3≤8

х²-4х-5≤0

х= -1; х=5

+ - +

-1 5

Х є [-1;5]

log₃( 8-х)=0,

4-х ≠ 0;

х=7,

х ≠4.

Х є(-∞;4)U[7;∞)

Завдання №5

«От так парадокс !» (парадокс – це незвичайна думка, що різко розходиться із загальноприйнятою думкою стосовно даного питання). Розгляньте розв’язання даного завдання та проаналізуйте, де допущена помилка.

2>3 ???

( ½ )²> ( ½ )³

lg(½ )²>lg ( ½ )³

2 lg(½ )>3lg ( ½ ) |: lg ( ½ )

2>3

У чому помилка?

У цій нерівності lg ( ½ )0, тому при діленні на lg ( ½ )знак нерівності змінюється на протилежний.

ІІ етап – 15 хв

виконання самостійної роботи на розв’язування логарифмічних рівнянь та нерівностей.

Номер прикладу відповідає порядковому номеру прізвища студента у журналі (або закінчується даною цифрою)

Розв’язати рівняння:

;
;
+=
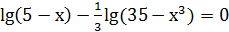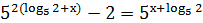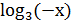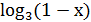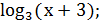
2=;
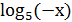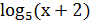2×=
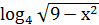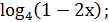
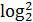(х-1)-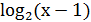=2;
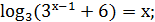
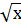×=0;
+ =;
+ = .

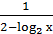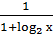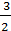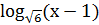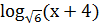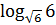Розв’язати нерівність:

1. (х-1)×

2.-2х-3)≥;

3. × ≤ 9;

4. +≥;

5. ≥ 1;

6. ≥2;

7. ≥2;

8. + -2 ≥0;

9. ≤0;

10. ≥ 1.

Робота виконується у міні-підручнику і здається для перевірки викладачеві, .

ІІІ етап. Захист творчої роботи. 5 хв.

Наприкінці заняття проходить фрагмент захисту творчої роботи студента Сипко Максима «Графічні фантазії», де віа доводить, що математика і мистецтво - дві грані одного і того ж процесу – творчості, а також показує взаємозв’язок між цими різними дисциплінами за допомогою графіків функцій та зображення масок. У своїй роботі він створив ескіз мексиканської маски за допомогою графіків логарифмічних та показникових функцій (презентація, слайди 10- 17).

2.6. Підсумок заняття: 7 хв.

виставлення оцінок за роботу в міні-підручнику та за самостійну роботу.

Ну от, друзі , закінчилася наша подорож в чарівний світ логарифмів. І якщо хто з вас не зміг розв’язати приклад - не сумуйте, бо ми з вами тільки вчимось і тільки завдяки своєї наполегливості зможемо познати щось нове та невідоме.

2.7. Повідомлення домашнього заняття 3 хв.

Повторити означення та властивості логарифмічної функції, розв’язати: ; ; ; побудувати графік: підготуватись до контрольної роботи