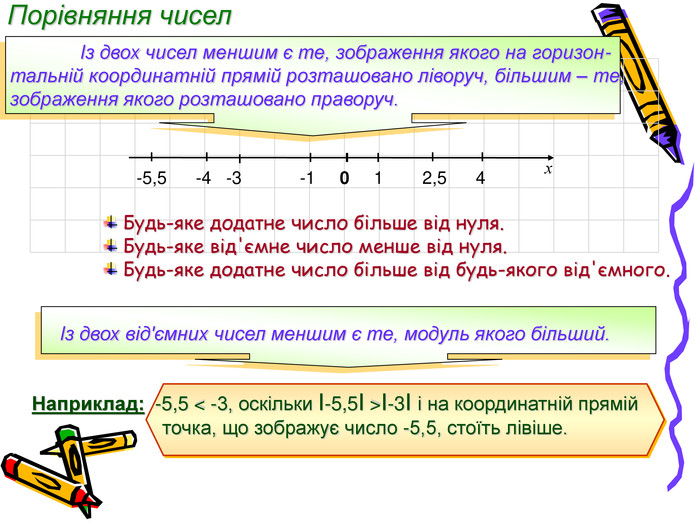
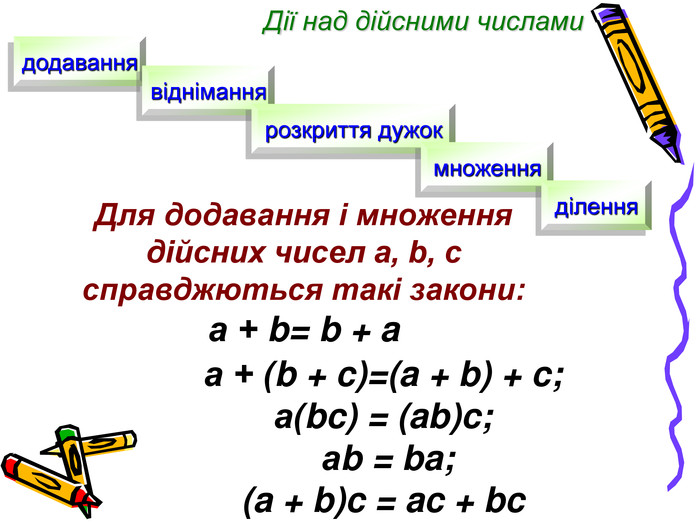
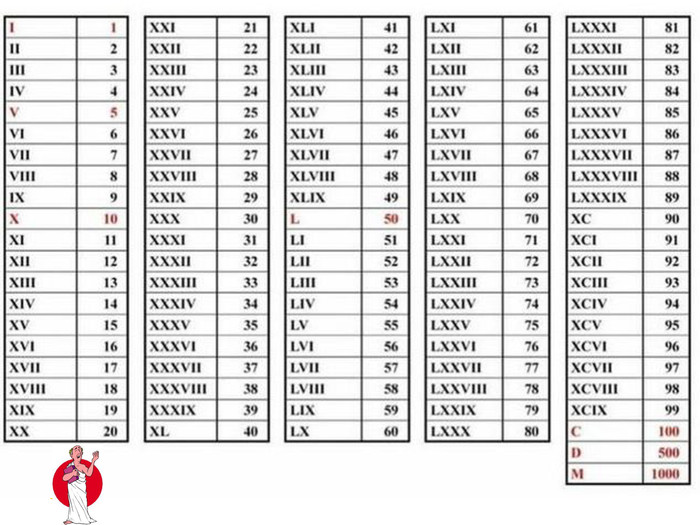
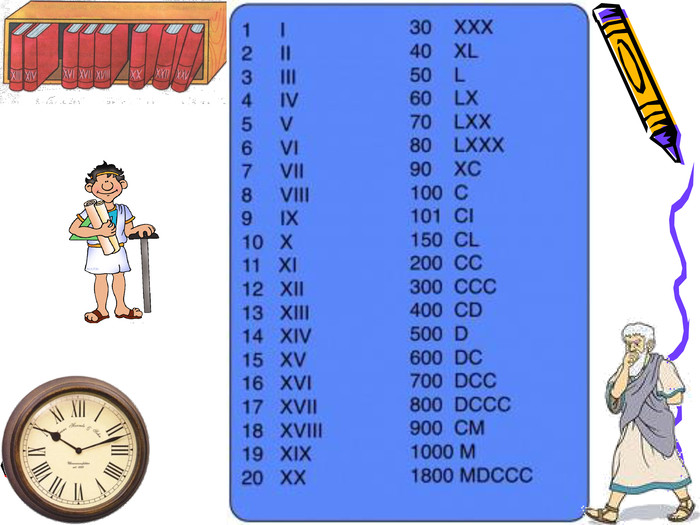
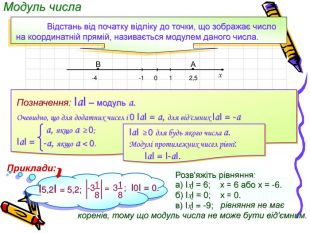
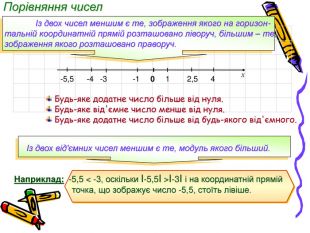
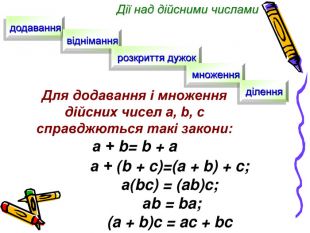
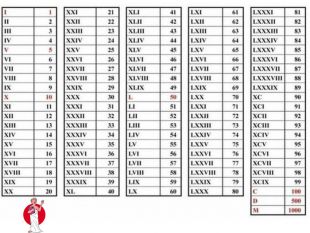
Заняття з алгебри, Презентація, тема "Дійсні числа та дії з ними. Відсоткові розрахунки"
Про матеріал
Заняття з алгебри, 10 клас, Презентація, тема "Дійсні числа та дії з ними. Відсоткові розрахунки" Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку