ЗАСТОСУВАННЯ ПОКАЗНИКОВОЇ ТА ЛОГАРИФМІЧНОЇ ФУНКЦІЙ
Методична розробка
уроку на тему:
«ЗАСТОСУВАННЯ ПОКАЗНИКОВОЇ ТА ЛОГАРИФМІЧНОЇ ФУНКЦІЙ»

Тема уроку: ЗАСТОСУВАННЯ ПОКАЗНИКОВОЇ ТА ЛОГАРИФМІЧНОЇ ФУНКЦІЙ
Мета уроку: узагальнити та систематизувати знання учнів з теми «Показникова та логарифмічна функція», показати учням практичне значення теми в житті; викликати в учнів зацікавленість предметом алгебри, бажання вивчати його;
стимулювати пізнавальну діяльність учнів, сприяти формуванню і розвитку системних знань, колективних і міжособистісних відносин;
розвивати вміння узагальнювати, мислити логічно, робити висновки, чітко висловлювати свою думку;
виховувати відповідальність, уміння працювати самостійно й у групі.
Тип уроку: узагальнення та систематизації знань, урок-захист проекту.
Обладнання: план-конспект, роздатковий матеріал (буклети), презентація, проектор, комп’ютер.
Хід уроку
І. Організаційний момент.

ІI. Актуалізація опорних знань.
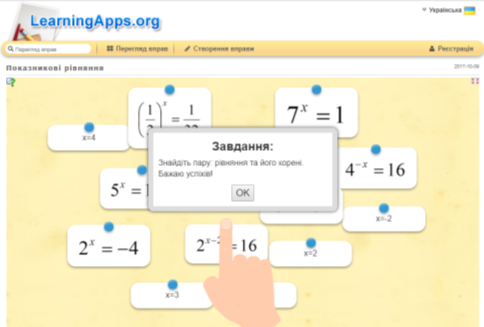
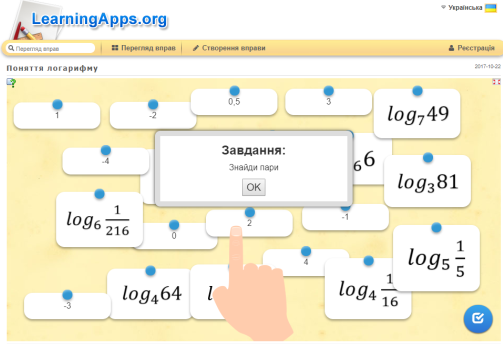
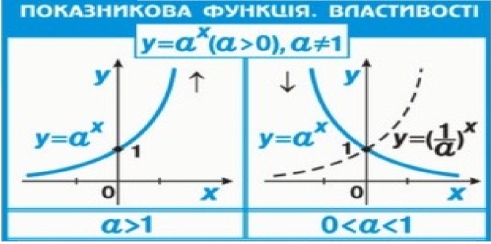
Робота із завданнями інтернет-ресурсу https://learningapps.org/ на повторення властивостей показникової та логарифмічної функції
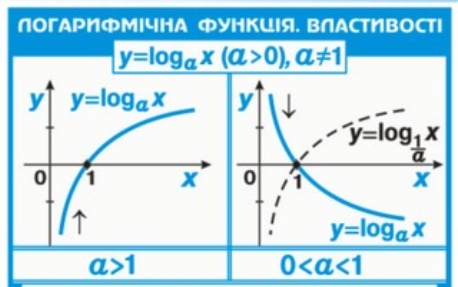
ІIІ. Повідомлення теми, мети і завдань уроку.
Захист проекту: «Застосування показникової та логарифмічної функцій»

ІV. Захист проекту.
Кожна група представляє результати своєї пошукової діяльності.
Показникова функція у банківській справі

Ще за стародавніх часів було широко поширене лихварство — віддавання грошей у позику під відсотки. Селянин у разі неврожаю, ремісник, майно якого знищила пожежа, розорений торгівець змушені були йти до лихваря, обіцяючи наступного року повернути суму значно більшу, ніж узята в позику. Наприклад, у Давньому Вавилоні лихварі брали по 20 % лихви на рік. При цьому, якщо боржник не міг повернути борг наступного року, йому треба було платити відсотки не тільки з позиченого капіталу, а й з відсотків, що виросли за рік. Тому через 2 роки слід було заплатити не 40 %, а 44 %лихви, адже 1,22 = 1,44. За 5 років сума боргу збільшувалася в 1,25 разів, тобто майже в 2,5 рази, а за 10 – років більш ніж у 6 разів. Зрозуміло, що більшість боржників були не в змозі повернути борг і, давно виплативши основну суму боргу, були змушені все життя працювати на те, щоб виплатити все зростаючі відсотки. Нарешті зубожілі боржники ставали рабами хижого лихваря.
У XIV—XV ст. у Західній Європі почали з'являтися банки (від фр. banque — лава, контора) — установи, які давали гроші в позику князям та купцям, фінансували за великі відсотки далекі мандрівки та завойовницькі походи. Щоб полегшити розрахунки складних відсотків, склали таблиці, за якими відразу можна було дізнатися, яку суму треба виплатити через п років, якщо була взята сума а під p% річних. Легко підрахувати, що сума, яку треба заплатити, виражається формулою: ![]()
Якщо р — стале, то S є функцією від п. Такі таблиці давали значення показникової функції при різних значеннях основи ![]() і натуральних значеннях п.
і натуральних значеннях п.
Останнє обмеження було не дуже зручним: іноді гроші бралися в борг не на ціле число років, а, наприклад, на 2 чи 6 місяців. Так виникла ідея степеня з дробовим показником. Ця ідея належала ще Архімеду, але вона не була зрозумілою його сучасникам. І лише через 1,5 тисячоліття почали розглядати піднесення чисел до степеня з дробовим показником.
Показникова функція в літературі

У романі Жуля Верна „Матіас Шандор” виведено образ силача Матіфу, який здійснив багато подвигів. Ось один із них.
Готувався спуск на воду корабля. І саме в цей момент до гавані влетіла яхта, яка неминуче врізалася б у корабель, якби з натовпу не вибіг чоловік, який з усієї сили вперся в землю ногами і вчепився в трос, що утримував корабель, щоб затримати спуск. Поблизу стояла гармата. Сміливець швидко накинув на неї трос і з нелюдським зусиллям утримував його 10 секунд, поки трос не лопнув. Але цих 10 секунд було досить, щоб яхта проскочила повз корабель — зіткнення не сталося. Звичайно, ви здогадалися, що сміливий незнайомець — це Матіфу.
Але чи потрібна нелюдська сила, щоб утримати корабель?
„Чи може людина втримати корабель?”
Згадаємо, як відбувається швартування корабля. З нього кидають канат на берег. Людина, що стоїть на пристані, обмотує кілька разів канат навколо стовпа. Сила тертя між канатом і стовпом і утримує судно.
Якщо F0 — прикладена сила, F— сила, що утримує корабель, то маємо:
x витків: F= F0 • kx;
k залежить від матеріалу, з якого зроблено канат і стовп.
Тобто, обернувши канат 3 рази, силою 22 Н можна утримувати 40 т.
Різноманітні застосування показникової і логарифмічної функцій надихнули англійського поета Елмера Брілла на написання "Оди експоненті".
Були поети, які не присвячували од логарифмам, але згадували їх в своїх віршах.
У вірші "Фізики і лірики" Борис Слуцький написав:
Потому-то, словно пена,
Опадают наши рифмы.
И величие степенно
Отступает в логарифмы.

Показникова функція в біології
Показникова функція має широке застосування в біології. Розглянемо кілька прикладів.
Розглянемо, як зростає популяція бактерій у відповідності з простим життєвим циклом. При цьому час між моментом поділу материнської клітини (народження нової) і моментом, коли вона сама ділиться, називається періодом поділу, або часом генерації.
ЗАДАЧА. Нехай число бактерій у культурі становить А0. За час однієї генерації всі ці А0 бактерій поділяться навпіл і утвориться 2А0 бактерій. Через дві генерації їх стане 2 • 2А0, через три — 2 • 2 • 2А0 і т.д. Через р генерацій А = 2Р • А0.
Нехай час однієї генерації Т, тоді ![]() , де t час з початку розподілу.
, де t час з початку розподілу. ![]() .
.
Бачимо, що популяція росте за показниковим законом, або, як кажуть, експоненціально (лат. exponense — той, хто показує).
Саме здатність бактерій до швидкого розмноження забезпечує їх кількісну перевагу серед живих форм. Якби не було природних причин, що заважали б вибухам кількості бактерій, сумарна маса яких становила б декілька десятків тисяч тонн, а за дві доби показникового зростання маса однієї бактерії перевищила б у декілька разів масу Земної кулі. Наша планета, проте, не перетворилася на суцільну масу мікробів. І це не тільки тому, що бактерії вичерпують поживні речовини, які підтримують їх зростання, а й тому, що при зростанні вони виділяють велику кількість продуктів, токсичних для них самих.
Звичайно, показниковий закон виконується дуже приблизно в біологічних системах, бо ми маємо тут справу з дуже складними системами.
ЗАДАЧА. За законом показникової функції розмножувалося б все живе на Землі, якби для цього були сприятливі умови, тобто не було природних ворогів і було вдосталь їжі. Доказ тому-поширення в Австралії кроликів, яких там раніше не було. Досить було випустити пару особин, як через деякий час їх потомство стало національним лихом.
ЗАДАЧА. Якби всі макові зерна давали сходи, то через 5 років число "нащадків" однієї рослини дорівнювало б 243 • 1015або приблизно 2000 рослин на 1 м суші.
ЗАДАЧА. Потомство кімнатних мух за літо тільки від однієї самки може скласти 8 • 1014. Ці мухи важили б кілька мільйонів тонн, а вибудувані в один ланцюжок, вони склали б відстань, більшу, ніж відстань від Землі до Сонця. Потомство пари мух за 2 роки мало б масу, що перевищує масу земної кулі. І тільки завдяки спільноті тварин і рослин, коли збільшення одного виду тягне за собою зростання кількості його ворогів, встановлюється динамічна рівновага в природі.

Логарифми в архітектурі
У 2006 році в мексиканському місті Наукальпан-де-Хуарес був побудований унікальний будинку у вигляді мушлі. Побудова будинку у вигляді морської мушлі в Мехіко базується на формулі логарифмічної спіралі. Творці Наутилуса - так називається проект - спробували створити відчуття четвертого виміру, яке повинне виникати, якщо знаходитися всередині будівлі.
Фасад прикрашений різнобарвним склом, завдяки якому всередину проникає багато світла, - на стінах лежать різнокольорові відблиски. Але це не сама незвичайна деталь. Увійшовши до будинку, гість бачить перед собою суцільний трав'яний «килим», по якому петляють доріжки, вимощені каменем. Ці стежки ведуть до житлових кімнат.
Круглі вікна і плавні лінії стін створюють враження, ніби будинок - справжня мушля, яка лежить на дні моря. Це особливо відчувається у ванній кімнаті, де стіни пісочного і блакитного кольорів шорсткі на дотик, а вікна розташовані високо над головою.
Матеріал, з якого побудований «Наутілус», - так званий Grancrete (granite, «граніт» + concrete, «бетон»). Це особливий вид міцної вогнетривкої кераміки, здатний витримувати екстремальні погодні умови.
Крім того, житло майже не вимагає витрат на утримання. Мешканці економлять на опаленні і кондиціонерах, оскільки для вентиляції передбачені два підземних воздуховода. Влітку повітря з вулиці, пройшовши по одному з каналів, остигає і охолоджує приміщення, а взимку, навпаки, нагріває.


Логарифми в біології, зокрема в людському тілі


Особливості логарифмічної спіралі вражали не лише математиків. Їх геометричні властивості, зокрема інваріантність(збереження кута), дивує і біологів. Вони вважають саме цю спіраль свого роду стандартом біологічних об'єктів різного походження. Логарифмічна спіраль – єдиний тип спіралі, яка не змінює своєї форми при збільшенні розмірів. Ця властивість пояснює чому логарифмічна спіраль так часто зустрічається у природі.
(соняшник, ананас, молюски)
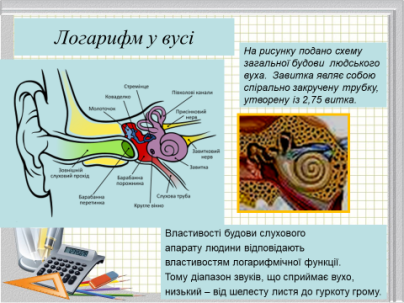
Людське вухо
На рисунку подано схему загальної будови людського вуха. Завитка являє собою спірально закручену трубку, утворену із 2,75 витка.
Властивості будови слухового апарату людини відповідають властивостям логарифмічної функції.
Тому діапазон звуків, що сприймає вухо, низький – від шелесту листя до гуркоту грому.
Логарифми у Всесвіті
Гучність шуму і яскравість зір оцінюються однаковим чином – по логарифмічній шкалі.
По логарифмічній спіралі закручена Галактика, якій належить Сонячна система. “Величина” зірки являє собою логарифм її фізичної яскравості.
Оцінюючи яскравість зір, астроном оперує таблицею логарифмів, складених при основі 2,5.
Гучність виражена у белах, дорівнює десятковому логарифму відповідної фізичної величини.
V. Підсумки уроку.
Виставлення оцінок: керівник кожної групи сам оцінює роботу членів своєї групи, виставляючи оцінки.
VІ. Домашнє завдання.
Підготуватися до контрольної роботи.
Домашня самостійна робота
Розв’язати показникові та логарифмічні рівняння:
![]()
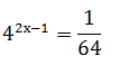
![]()
![]()


про публікацію авторської розробки
Додати розробку
