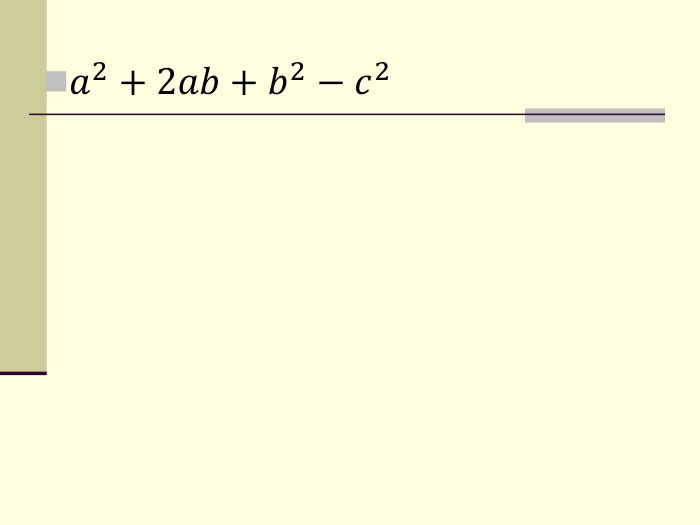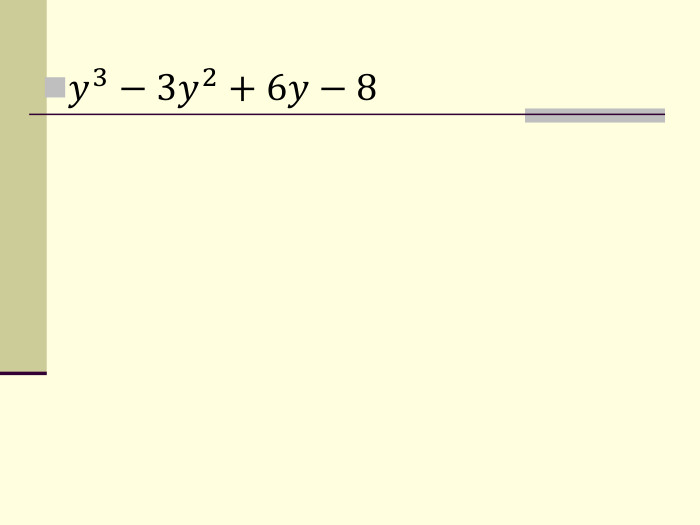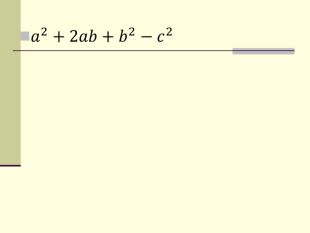Застосування різних способів розкладання многочленів на множники
Про матеріал
Формування компетентностей:
Предметна компетентність :
вивчити формули скороченого множення: квадрат двочлена, різниця квадратів,
сума і різниця кубів, куб суми і різниці двох виразів;
домогтися свідомого розуміння учнями змісту формул скороченого множення;
виробити вміння записувати, читати та застосовувати формули для розв'язування
вправ;
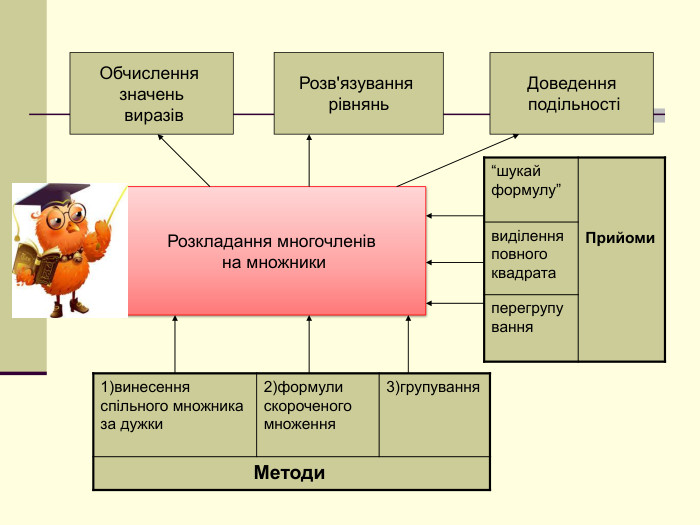
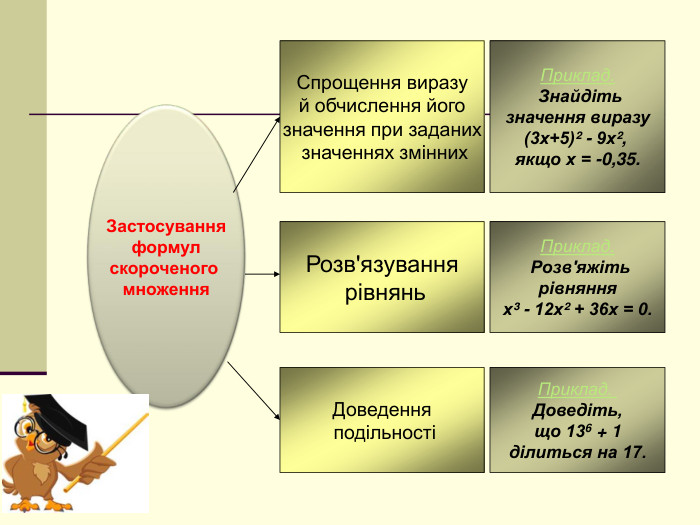
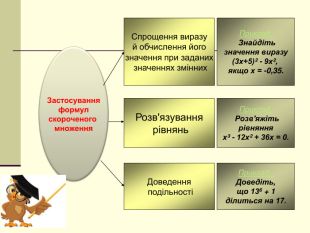
формувати вміння та навички застосовування цих формул для спрощення виразів,
розв'язування рівнянь, доведення тотожностей, доведення подільності;
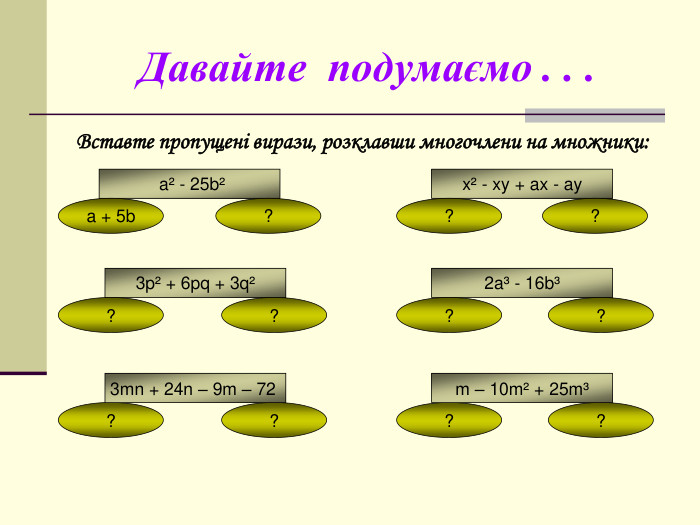
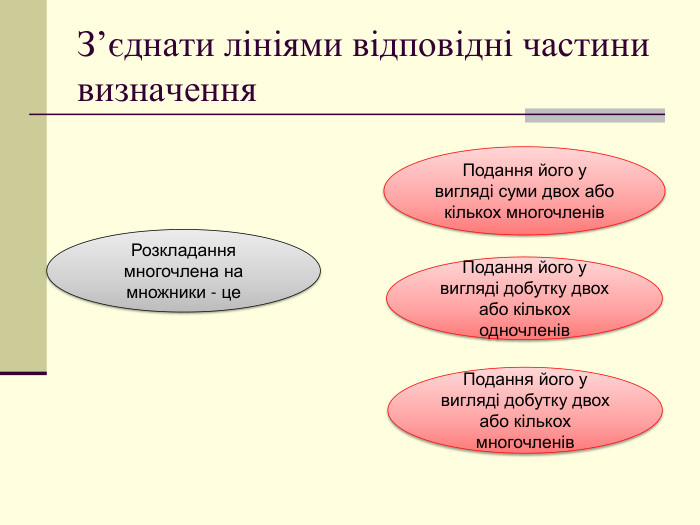
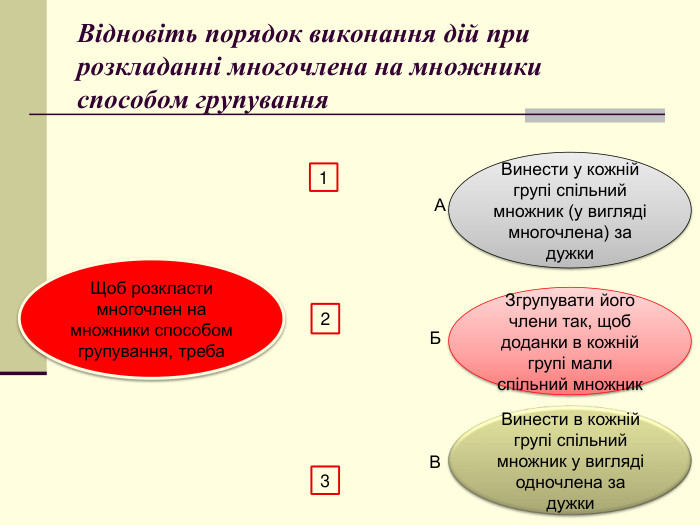
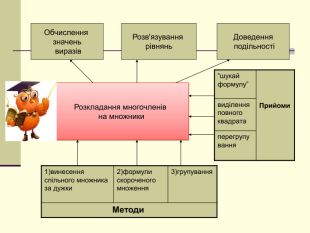
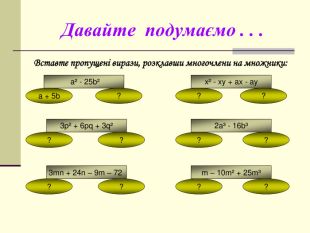
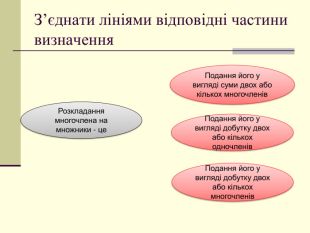
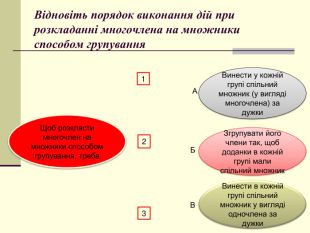
формувати вміння ти навички виконувати розкладання многочленів на множники
за формулами скороченого множення та із застосуванням декількох способів Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку