Застосування розв’язування прямокутних трикутників у прикладних задачах
Тема уроку: Застосування розв’язування прямокутних трикутників у прикладних задачах.
Мета уроку: узагальнити і систематизувати знання з даної теми; повторити означення синуса, косинуса, тангенса і котангенса гострого кута прямокутного трикутника, теорему Піфагора та основні наслідки з неї; закріпити вміння і навички застосувати теоретичний матеріал до розв'язування прямокутних трикутників; показати практично-прикладний характер здобутих знань; розвиток міжпредметних зв'язків; виховання пізнавального інтересу до вивчення математики.
Тип уроку:урок узагальнення та систематизації знань.
Очікувані результати: мати уявлення про синус, косинус, тангенс гострого кута прямокутного трикутника; застосовувати теорему Піфагора та тригонометричні співвідношення при розв’язуванні прямокутних трикутників.
Хід уроку:
І. Організаційний момент
ІІ. Мотивація навчальної діяльності. Оголошення теми та мети уроку.
Вчитель веде діалог з дітьми про те, що на уроці має бути і для чого це все потрібно нам у житті.
Вправа: Сходинки до успіху. (див. презентація, слайд №1)
Дітям дається задача протягом уроку досягти останньої сходинки «Успіх» (див на малюнку у презентації)
Вправа: Дерево настрою
Діти повинні на дереві настрою прикріпити смайлик з наданих їм, який відповідає настрою на початку уроку.
ІІІ. Перевірка домашнього завдання.
Перевірка письмового завдання здійснюють відповідальні учні
ІV. Актуалізація опорних знань
В цей час деякі учні можуть виконувати тестові завдання або самостійну роботу
1. Геометричне доміно
Правила: На кожній парті лежить по одній картці доміно з запитаннями та відповідями. Починає той, у кого слово СТАРТ. Читається запитання, а інші учасники шукають відповідь на своїх картках. Зачитують її. Якщо відповідь вірна, то читають наступне запитання уже з своєї картки. І так до картки з словом ФІНІШ
У таблиці нижче подані зразки карток доміно, які можна використати на уроці.
|
СТАРТ |
… він має прямий кут |
… сторони прямокутного трикутника, які утворюють прямий кут |
|
Трикутник називається прямокутним, якщо… |
Катетами називають… |
Косинусом гострого кута прямокутного трикутника називають … |
|
… відношення прилеглого катета до гіпотенузи. |
… сторона прямокутного трикутника, яка лежить навпроти прямого кута |
… сумі квадратів катетів |
|
Гіпотенузою називається…. |
Квадрат гіпотенузи дорівнює… |
Тангенсом гострого кута прямокутного трикутника називають … |
|
… відношення протилежного катета до прилеглого. |
…дев’яносто градусів |
… відношення протилежного катета до гіпотенузи. |
|
Сума гострих кутів прямокутного трикутника дорівнює… |
Синусом гострого кута прямокутного трикутника називають … |
Синус і косинус кута не можуть бути… |
|
… більшими за одиницю |
… відношення прилеглого катета до протилежного. |
… дорівнює половині гіпотенузи |
|
Котангенсом гострого кута прямокутного трикутника називають … |
Катет, який лежить навпроти кута 30 градусів … |
При зростанні гострого кута косинус і котангенс… |
|
… спадає від 1 до 0 |
… = 1 |
… зростає від 0 до 1 |
|
sin2 ∝ + cos2 ∝ = |
При зростанні гострого кута синус і тангенс… |
ФІНІШ |
2. «Вірус»
Учням показується картинка з формулами з помилками і говориться, що комп’ютерний вірус пошкодив файл з формулами, а їм потрібно все виправити. ( див. додаток, слайд №3)
|
З помилками |
Правильно |
|
sin ∝ + cos ∝ = 1
tg ∝ + ctg ∝ = 1
sin ∝ = cos( −∝) |
sin2 ∝ + cos2 ∝ = 1
tg ∝ ∙ ctg ∝ = 1
sin ∝ = cos(90°−∝) |
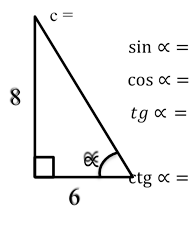
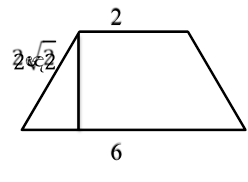
3. Розв’язування усних вправ за готовим рисунком
( див. додаток, слайд №4 – 6)
|
|
|
c =
β = |
|
|
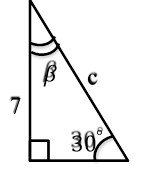
α = β = x = |
|
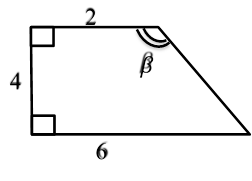
α = β = h = |
|
4. Лото «Пізанська вежа»
Картинка пізанської вежі розрізана на частини, на яких з іншого боку написані відповідні значення та завдання, які мають відповідати завданням та значенням на дошці (в умові). В таблиці подані значення і відповіді. Ліва частина – умова, права частина – відповіді, які знаходяться на частинках картини (зображені дзеркально, як це виглядає на протилежній стороні картинки) . Учні підходять до дошки, обирають частинку картинки з відповіддю або завданням і шукають відповідну клітинку на дошці (в умові).
|
sin 60° = |
tg 30° = |
|
sin 30° = |
|
|
|
|
|
= 0 |
cos 60° = |
|
tg 45° − 1 = |
cos 30° = |
|
|
sin 45° = |
ctg 30° = |
= 1 |
ctg 45° = |
= √3 |
|
|
|
= √3 |
|
tg 45° = |
= 1 |
cos 45° = |
tg 60° = |
Показ відео про вежу
V. Узагальнення та систематизація знань. Розв’язування задач
Задача №1 «Пізанська вежа» ( див. додаток, слайд №7)
Як ми бачили у відео вежу намагались вирівняти. Але вона все рівно залишилась нахилена, що тепер привертає увагу туристів.
Наше завдання:
визначити кут нахилу вежі, якщо нам відома її висота – 56 м і те, що вершина
вежі була відхилена на відстань приблизно 5 м від центру Розв’язання:
∝ = 5°6′
Щоб вимірювати кути на місцевості користуються приладом – астролябія або теодоліт. (Див. мал. , додаток, слайд №8, 9) Доповідь учнів.
Задача
№2. ( див. додаток, слайд №10)
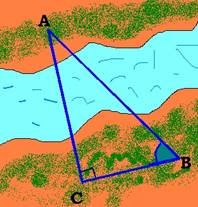
Як виміряти відстань з місця А до місця В, між якими протікає річка, якщо здійснено виміри: АВС = 54° і
відстань ВС =45 м.
Розв’язання:
АС = ВС ∙ t𝑔 В = 45 ∙ t𝑔 54° = 45 ∙ 1,3764 ≈ 62 (м)
Задача №3. «Ескалатор»
( див. додаток, слайд №11,
12)
Ескалатор метрополітену містить 170 східців від вестибюля до підлоги підземної станції. Ширина сходинки ескалатора – 40 см, висота – 20 см. Обчисліть глибину станції та кут нахилу ескалатора. Знайдіть орієнтовний час спуску на ескалаторі, якщо його швидкість приблизно дорівнює 0,5 м/с.
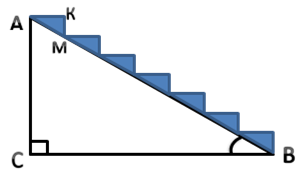Дано: ∆ АВС – прямокутний,
АК = 40 см, КМ = 20 см, n = 170, V = 0,5 м/с
Знайти: АС, АВС, t
Розв’язання:
1. ВС = 170 ∙ АК = 170 ∙ 40 = 6800 (см) = 68 (м)
2. АС = 170 ∙ МК = 170 ∙ 20 = 3400 (см) = 34 (м)
3. tg В = АС: ВС =0,5, отже АВС = 26°34′
4.
АВ = 
5.
Відповідь: 34 м, 26°34′, 2 хв 30 с
Додаткові задачі
Задача №1
За 800 метрів від місця підйому літака прямо по курсу видно дерева, висота яких 20 метрів. Під яким кутом має злетіти літак, щоб не зачепити верхівки дерев.
Розв’язання: 
, отже ∝ = 1°43′
Відповідь: 1°43′
Задача №2
Висота Сонця 48°. Довжина тіні телевежі = 76 метрів. Знайти висоту телевежі.
Розв’язання: ℎ = 76 ∙ t𝑔 48° = 76 ∙ 1,1106 ≈ 84,056 (м)
Відповідь: 84,056 м
Задача №3
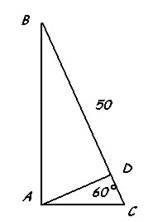
Знайти ширину водоймища між точками, одна з яких знаходиться на відстані 20 м від нашого місцезнаходження і відхилена на захід на 32 °, а друга — відхилена схід кут 28° і знаходиться на відстані 50 м від нас.
Дано: ∆АВС, ВС = 50 м, АС = 20 м, АСВ = 60°.
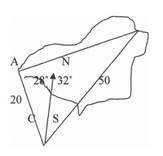Знайти: АВ
Розв'язання.
1. Проведено висоту AD; AD BC.
2.
∆АDC: D = 90°, DC=AC ∙ 
cos60°=10 (м)
AD =AC 
3. За аксіомою планіметрії :ВС= BD + CD, тому BD = ВС - CD = 40(м).
4. ∆ABD: D= 90°. За теоремою Піфагора:
АВ2 = AD2 + BD2 = 300 +1600 = 1900; АВ = 10√19 (м)
Відповідь: 10√19 м.
VІ. Підсумок уроку ( див. додаток, слайд №15)
1. Гра «Вірю, не вірю»
Чи
вірите ви, що з 24 сірників можна скласти прямокутний трикутник?
Чи
вірите ви. Що існує прямокутний трикутник з сторонами 4, 5 і 9?
Чи вірите ви, що ромб можна
розділити на 4 рівних прямокутних трикутника?
Чи
вірите ви, що на місцевості можна визначити ширину озера?
2. Усні задачі:
Ø Як перевірити, чи має даний шмат тканини форму прямокутного трикутника?
Ø Як від прямокутної дошки відрізати частину під кутом 45°?
Ø Як за допомогою мотузки в Стародавньому Єгипті відкладали прямі кути?
3. Виставлення оцінок
VІІ. Рефлексія
Дерево настрою (учні
відтворюють свій настрій, з допомогою смайликів, на кінець уроку і
спостерігають за змінами на дереві) Що
вам дав сьогоднішній урок Чим
він вам запам’ятався?
Що потрібно знати для
розв’язування прямокутних трикутників?
Вправа «Сходинки до
успіху». Якої сходинки Ви досягли? Чому? Чи досягли Ви кінцевої сходинки
«Успіх». ( див. додаток, слайд №16)
VІІІ. Домашнє завдання ( див. додаток, слайд №17)
За підручником Геометрія. 8 клас: Підруч. для загальноосвіт. навч. закл. / А.П.Єршова, В.В.Голобородько, О.Ф.Крижановський, С.В.Єршов. — X.: АН ГРО ПЛЮС, 2008.
§18-21 – повторити
№ 737, 736 – середній та достатній рівень, №741 – високий рівень
про публікацію авторської розробки
Додати розробку