Застосування розвязування трикутників у прикладних задачах

                                                   

Тема уроку

 

Застосування розв’язування трикутників у прикладних задачах.

 

Урок геометрії у 9 класі.

 

Ванда Пашкова, учитель математики спеціалізованої школи І–ІІІ ст.№196, м. Київ.

 

Мета уроку: систематизувати й узагальнити знання учнів із теми                   «Розв’язування трикутників»; 

  формувати в учнів уміння і навички творчого застосування знань та умінь розв’язування трикутників до вирішення прикладних задач; поглиблювати та розширювати діапазон знань з теми; виховувати працелюбність, почуття товариськості, взаєморозуміння та взаємодопомоги, розвивати прагнення до знань, та сприяти усвідомленню учнями важливості розуміння прикладних задач у повсякденному житті.  Зацікавити учнів проектом, створити творчі групи, визначити коло обов’язків кожного з них, учити учнів самостійно працювати над  завданнями прикладного характеру .

 

Тип уроку: Урок узагальнення та систематизація знань.

 

Обладнання та наочність: картки із завданнями для груп, калькулятори, таблиці Брадіса, інтерактивна дошка, презентації, практичні задачі в малюнках, портрети вчених, картки самооцінювання та оцінювання.

 

Математику слід вивчати у школі ще й з тією метою, щоб одержані тут знання

були достатні для звичайних потреб у житті.

                                                                                                                      М. І. Лобачевський

Хід уроку

 

І. Організаційний етап

 

ІІ Повідомлення теми і мети уроку

Учні класу були заздалегідь поділені на чотири групи. У кожній групі є теоретики, дослідники і практики. Кожна з груп повідомляє теорію, яку закріплює практикою. Учні однієї з груп розповідатимуть, як знайти відстань між двома доступними пунктами, другої – як знайти відстань до недоступного пункту,  третьої-як знайти висоту предмета, основа якого недоступна,  четвертої-як знайти відстань між двома недоступними пунктами.

У кожного учня на парті є таблиця, в якій вказано у скільки балів оцінюється кожне правильно розв’язане  завдання.   

Учні самостійно занотовують кількість набраних балів за кожен вид роботи. Підсумовують кількість балів, переводять їх в оцінку і оголошують результати в кінці уроку.

Учитель повідомляє учням тему і мету уроку, називає групи,  напрями їх діяльності.

 

 V. Мотивація навчальної діяльності

Учитель:

    Чи потрібно уміти розв’язувати трикутник? Де можна використати знання з цієї теми? Сьогодні на уроці ми повторимо основні види задач на розв’язування трикутників, способи їх розв’язання і спробуємо з вами провести невелике дослідження в межах  розв’язування практичних задач з теми «Розв’язування трикутників», а також переконатися у тому, що, дійсно, такі знання потрібні. Як відомо не завжди вдається знайти висоту, відстань, глибину, або інші розміри реального об’єкту безпосереднім вимірюванням, а інколи це взагалі неможливо. Звертаю вашу увагу на ці малюнки. Чи можна, на вашу думку, виміряти параметри даних  об’єктів? Звичайно, це зробити дуже важко, так як вони малодоступні.

 

А оскільки відповідні розміри потрібно знати, то ми сьогодні спробуємо розібратися, як у конкретній ситуації можуть допомогти знання з математики. Існує ряд практичних ситуацій, у яких необхідно використати тригонометрію для визначення невідомих сторін і кутів трикутника, а  оскільки знання стають міцнішими, якщо їх застосовувати в практичній діяльності, то сьогодні проведемо урок практичного застосування знань з теми «Розв’язування трикутників.»  

 

 

 

 

ІV. Актуалізація опорних знань.

Метод «Мікрофон»

(Представники кожної команди ставлять по черзі запитання учням інших команд. Якщо учні команди не відповідають на задане питання або дають непраевильну відповідь,то запитання адресується учням інших команд).

Питання на які повинні відповісти учні:

1. Що означає розв’язати  трикутник?
2. Які можливі види задач, у яких вимагається розв’язати трикутник?
3. Сформулювати теорему косинусів.
4. Сформулювати дві задачі, які можна розв’язати за теоремою косинусів.
5. Як визначити вид трикутника( гострокутний, прямокутний чи тупокутний) за трьома сторонами?
6. Сформулювати теорему синусів.
7.  Сформулювати дві задачі, які можна розв’язати за теоремою синусів.
8. Сформулювати наслідки з теореми синусів:

а)  про діаметр кола, описаного навколо трикутника,

б) співвідношення між кутами трикутника і його сторонами.

9. Скільки потрібно мати елементів, щоб розв’язати трикутник?
10. Яку властивість діагоналей паралелограма можна довести за допомогою теореми косинусів?

 

 

Відповіді: 1) знайти невідомі сторони і кути трикутника за відомими його сторонами і кутами;

2) а) за двома сторонами і кутом між ними;     

    б) за стороною і прилеглими до неї кутами;

     в) за трьома сторонами;

     г) за двома сторонами і кутом, протилежним до однієї з них;

3)квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними;

4) а) за теоремою косинусів можна знайти сторону трикутника за двома його сторонами і кутом між ними

(задача1);

      б) можна знайти кути трикутника за трьома його сторонами ( задача 2);

  5) кут трикутника гострий, прямий або тупий залежно від того, чи буде квадрат     протилежної сторони меншим, дорівнювати або бути більшим за суму квадратів двох інших сторін;

6)  сторони трикутника пропорційні синусам протилежних кутів;

7)  а) за стороною і прилеглими до неї кутами (задача 1), знаходити інші сторони і кути трикутника;

       б) за двома сторонами і кутом, протилежним одній з них(задача 2), знаходити інші сторони і кути трикутника;

8) а) у будь – якому трикутнику  відношення сторони до синуса протилежного кута дорівнює діаметру кола, описаному навколо трикутника;

     б) у трикутнику проти більшої сторони лежить більший кут, проти більшого кута лежить більша сторона;

9) три основні елементи трикутника, серед яких хоча б один був стороною трикутника;

10) сума діагоналей паралелограма дорівнює подвоєній сумі двох суміжних його сторін.

 

Усне виконання вправ (малюнки спроектовані на екран)

 

 а)   Допоможіть упіймати злочинця.

 

Працівникам поліції часто доводиться не тільки розшукувати, а й наздоганяти злочинців.

 

На пост ДАІ повідомили, що за кермом самоскида  злочинець. Він мчить по шосе із швидкістю близько 60Поліцейські з мотоциклом чекали на нього на перехресті доріг у точці А й помітили розшукуваний самоскид у точці   В. Як ви думаєте, якою дорогою мають їхати поліцейські, щоб одночасно із самоскидом бути в одній  і  тій самій точці шосе, якщо швидкість мотоцикла 120?

 

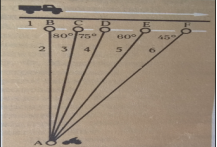
Відповідь: Дорога 2, очевидно, відпадає, тому треба обрати дорогу, відстань по якій до точки зустрічі має бути вдвічі більшою за ту, яку проїде за цей час самоскид. Легко здогадатися, що цю умову задовольняє дорога 5.

 

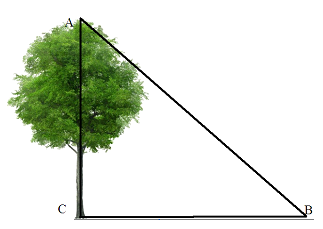
Учитель.  Допоможіть  Андрію. Поясніть, як знайти висоту дерева?

Відповідь учня. Вибираєм точку на вершині дерева ( точку А ), точку прямо під нею         ( точку С ), а також точку на землі ( точку В). Тоді можна виміряти кут АВС, сторону ВС, кут АСВ прямий.  Розв’язуючи прямокутний трикутник,  знайдемо висоту дерева.

                                

б) Гра «Знайди помилку» (розв’язки спроектовано на екран )

 

1. Тінь від найбільшого дерева України (це модрина, що росла в місті Рахів), висота якого 54 м, становила  36 м. Виразіть у градусах висоту сонця над горизонтом.

 

      Розв’язання.     

      Нехай ВС висота дерева, АС – довжина тіні.

Із прямокутного трикутника АВС: tg A= == 1,5; 

кут А=56º19',

Відповідь. Так дійсно, у цьому випадку висота сонця над  горизонтом становить 56º19'.

 

2. Найвищою архітектурною спорудою України є телевізійна вежа в місті Києві заввишки 385 м. Висота сонця над горизонтом становить 40º. Знайдіть довжину тіні, яку відкидає телевізійна вежа в цей момент.

 

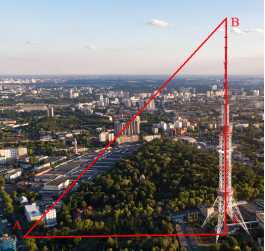
 Розв’язання. Із прямокутного трикутника АВС: АС = ВС· tg A;

АС=385·0,8391;  АС 323м.

Відповідь: В розв’язку допущено помилку,бо АС = ;  АС; отже АС458,8 м.

 

 

 в)Яку теорему треба використати, щоб розв’язати трикутник?

 

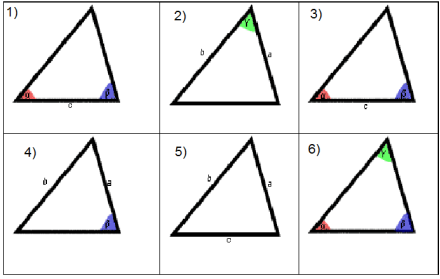
Відповіді: 1) Теорема синусів; 2) Теорема косинусів; 3) Теорема синусів; 4) Теорема синусів або теорема косинусів; 5) Теорема косинусів; 6) Неможливо розв’язати.

 

г) Знайти невідомі елементи трикутників.

 

 

 

 

 

 

 

 

 

 

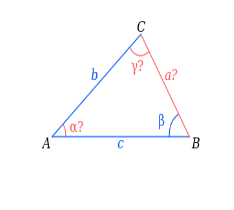Відповіді учнів:

1) cos= ;  cos; 

 

2) с =;   соs;   сos.

3); sin;  ;  а =.

 

Узагальнення та систематизація знань учнів.

 

Виступи учнів

 

Доповідь групи «Дослідники»

 

Дослідник

Тригонометричні формули використовують при проведенні різних вимірювальних робіт на місцевості. Наприклад, при вимірюванні висоти предмета і вимірюванні відстані до недоступної точки. Є професії, які потребують часто розв’язувати трикутники. У першу чергу, цим займаються геодезисти. Якщо заплановане велике будівництво, першими роботу починають геодезисти, щоб зняти план місцевості і охарактеризувати рельєф.

Коли ж на основі їх досліджень у проектних організаціях опрацюють проект, геодезисти знову міряють кути , розв’язують трикутники, забивають кілочки— «прив’язують» опрацьований проект до місцевості.

Ювелірна точність вимагається від геодезистів, які займаються підземними вимірюванням і зніманням, – маркшейдерів. Як справжні підземні штурмани вони задають напрями   прокладання тунелів, трас метрополітенів, гідротехнічних споруд і

 т. д.

 

 

Теоретик

Задача. Знайти відстань між двома доступними пунктами.

 

Якщо пункти А і В доступні, але безпосереднє вимірювання відстані між ними неможливе або утруднене, вибираємо зручний пункт С і вимірюємо сторони СА, СВ і кут АСВ трикутника АСВ, або одну з цих сторін і два прилеглі до неї кути. У першому випадку застосуємо теорему косинусів,  у  другому – синусів.

 

 

 

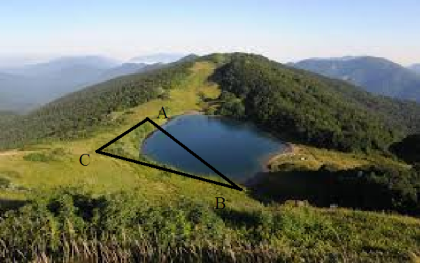
Практик

 

Нехай треба знайти відстань між двома пунктами, які знаходяться на протилежних берегах річки, а саме, знайти відстань від точки А до точки В за умови:

а) АС = 5м; ВС=7м;  кут С = 60º.

б)АС = 5м; кут С=60º; кут В =44º18'

 Розв’язання. (Розв’язок спроектовано на екран)

а)   Із трикутника АВС за теоремою косинусів:

АВ= АС + ВС - 2·АС·ВС·cosС.

АВ= 25+49- 2·5·7·cos 60º;

АВ= 74- 35 =39;

АВ=; АС6,2 м.

Відповідь: 6,2м.

б)  За теоремою синусів: ;  АВ=; АВ= 6,2м.

Відповідь: 6,2м.

 

Виступ групи « Допитливі»

 

Дослідники

Застосування у військовій справі.

 

Високо цінували застосування математики у військовій справі вітчизняні вчені і воєначальники. Уславленому полководцеві  О. В. Суворову належить блискучий афоризм: «Математика – гімнастика розуму». Великий полководець заради перемоги вмів усе розрахувати.

Теоретик

Задачі на знаходження відстані до недоступного пункту.

Якщо А і С – спостережні пункти, розміщені на відстані 1,5 – 2,5 км один від одного і недалеко від передової, то вони заздалегідь «прив’язані» і з них ведуться спостереження. Якщо там з’явиться ціль В, то її фіксують, тобто вимірюють кути і. Тоді залишається тільки розв’язати трикутник АВС за даними АС, і.

 

Практик (розв’язок спроектовано на екран).

1. Нехай треба знайти відстань від точки С до недоступного пункту В, якщо відстань від точки  А до вибраної точки на місцевості С дорівнює 8 м., кути спостереження ВАС і ВСА дорівнюють відповідно 94º і 56º.

( На місцевості кути спостереження можна виміряти з  допомогою астролябії.)

 

 

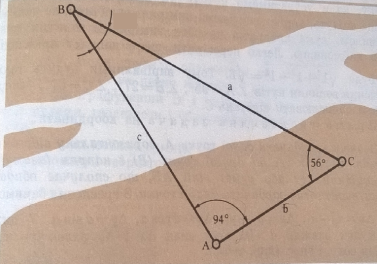
Розв’язання.

Із трикутника АВС маємо,   кут АВС = 180º-(94º+56º)=30º. За теоремою синусів: =, ВС=; sin94º=sin86º, sin86º0,9976, ВС (м).

Відповідь:

 

 

 

Виступ групи «Практики»

 

 

Дослідник

Щоб знайти висоту стовпа, дерева, башти, колони, водоспаду, будівлі, вежі, глибину озера, висоти гори і т. д.,  також приходиться розв’язувати  трикутник. В астрономії, щоб знайти відстань до найближчої зірки: вимірюють кути спостереження цієї зірки з протилежних точок земної орбіти з інтервалом у півроку і по їх різниці обчислюють шукану відстань. 

 

Теоретик

 

Задачі на знаходження висоти предмета, основа якого недоступна.

 

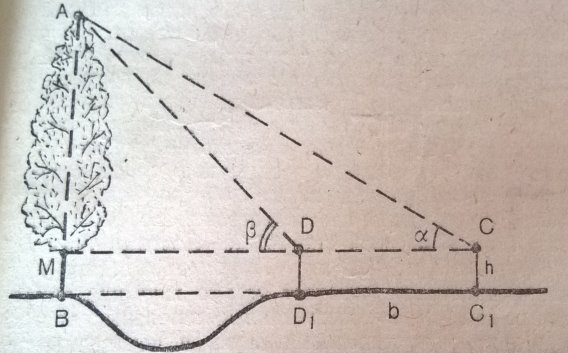
На горизонтальній прямій позначимо дві точки Сі D. Виміряємо його довжину, а також кути АСМ =, кут АDM=. Висоту приладу ССпозначимо h. За теоремою синусів, з трикутника АСD дістанемо: АD=. Із прямокутного трикутника АDМ маємо: АМ=AD·sin.Отже, АВ=+h. (1)

Виконавши відповідні розміри на місцевості, за формулою (1) можна знайти числовий результат.

Практик

Нехай результати вимірювання такі: b=2,5м, =36º, 42º, h=1,5м.

h=+1,5 ;  h(м).

  Відповідь: м.

 

Виступ групи «Всезнайки»

 

Дослідник

Щоб знайти  відстань між двома недоступними пунктами  доводиться розв’язувати трикутник.

 

Теоретик.

Задачі на знаходження відстані між двома недоступними пунктами.

Нехай А та В  - недоступні пункти. Вибираємо на місцевості таку точку   С, щоб з неї було видно пункти А і В,  а також – точку Д, з якої видно пункти А і В, вимірюємо  відстань СД та кути АСД, ВСД, АДС, ВДС. Тепер можемо,  скориставшись теоремою синусів знайти АД і ВД, а далі застосувати до трикутника  АВД теорему косинусів.

 

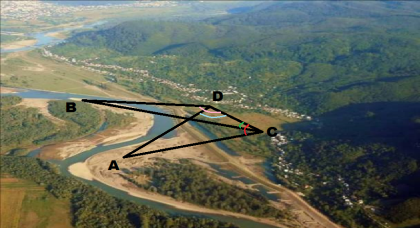
Практик ( розв’язок спроектовано на екран).

Нехай результати вимірювання такі:

 кути АСД ; ВСД; ВДС; АДС відповідно дорівнюють 100º; 75º; 80º; 50º. СД=12м.

Із трикутникаАСД: кут А =180º-(100º+50º)=30º. АД=; АД=; sin100º=sin80º; АД, АД23,6м.

Із трикутникаСВД: кут СВД=180-(80º+75º)=25º.  Sin25º0,4226. ВД= (м).

Кут АДВ=80º-50º=30º. АВ= АД+ВД- 2·АД·ВД·cosАДВ;

АВ23,6+27,4 - 2·23,6·27,4·0,866;

АВ=556,96+750,76 - 1120187,72.

АВ13,7 м.

Відповідь: 13,7 м.

 

  Учитель. (малюнок спроектовано на екран).

1).

 

 

Щоб виміряти глибину річки, геодезисти опускають у річку грузило, до якого привязані два шнури довжиною 1 і 1з гумовими кулями. Коли грузило опуститься на дно, кулі під дією течії відпливуть на певну відстань і зупиняться в точках К і К. Сфотографувавши їх і вимірявши на знімку відстань між кулями, геодезисти і обчислюють глибину h річки. Поясніть, як саме вони це роблять?

 

Відповідь учнів. З’єднати точки А, Кі К.Знайти кут між сторонами трикутника ККі 1за формулою cosВКК=, величину кута ВКК, знайти кут ВКА, із прямокутного трикутника АВК: h=1·sinВКА, обчисливши, знайти глибину річки.

 

 

2). Пояснити, як знайти відстань від берега до недоступної точки – наприклад до корабля.

 

 

 

 

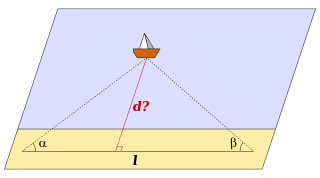
Відповідь: Треба відмітити на березі дві точки, відстань між якими відома, і виміряти кути між лінією яка з’єднує ці точки, і напрямом на корабель.  Тоді за відповідними даними можна знайти висоту трикутника.

 

Учитель.

Існують прилади, які допомагають визначити місцезнаходження будь – якого судна. Це  радіопеленгатор, радіолокатор.

 

Радіопеленгатор –  пристрій для радіопеленгу. («радіо» – випромінювання, промінь, «пеленг» – звучання).

 

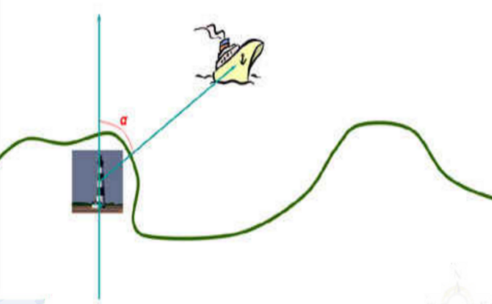
Радіопеленг – кут , утворений географічним меридіаном і напрямом від радіомаяка на радіолокаційну станцію, установлену на об’єкті (судні). Тобто, радіопеленгатор дозволяє обчислити кут.

 

 

 

 

 

Знаючи радіопеленги і об’єкта С з двох радіомаяків А і В, можна знайти радіопеленги і об’єкта по відношенню до лінії АВ. Це дає можливість звести задачу спостереження за об’єктом С до задачі розв’язку трикутника АВС.

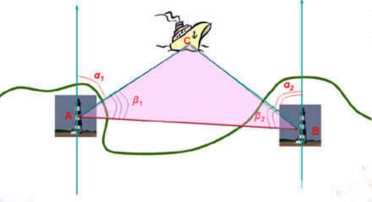
Наприклад:

В умовах поганої видимості з берегових радіомаяків А і В, відстань між якими 10 км запеленговано судно С. Знайти відстань від судна до кожного маяка, якщо з допомогою радіопеленгатора визначено кути САВ і СВА 45 градусів і 60 градусів відповідно.( Розв’язок спроектовано на екран).

 

 

Розв’язання: кут АСВ=180º- (45º+60º)=75º.

1) Із рівності знаходимо сторону ВС:

ВС=7,3(км).

2) Із рівності знаходимо сторону АС:

АС = = 9(км).

Відповідь: ВС7,3 км.; АС9км.

 

             Методи радіолокації застосовуються в багатьох галузях:

              у військовій справі (ПВО, точність стрільби),

              в морській, в повітряній і космічній навігації;

              в сейсмології;

              в метереології;

              при розвідці корисних копалин;

              при охороні об’єкта;

              в медицині.

Наприклад:

Задача із сейсмології 

Визначення епіцентру землетрусу

Сейсмологічною станцією С зафіксовано сильний підземний поштовх на відстані 100 км від станції під кутом 50 градусів до поверхні землі. Знайти глибину епіцентру h.

 

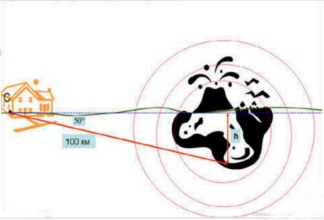
h=100·sin50º, h100·0,766; h76,6км.

Відповідь: 76,6км.

 

Робота в групах

 

Завдання кожної групи  - за 15 хвилин оперативно і правильно розв’язати задачі,

запропоновані вчителем. Кожен учень повинен вміти пояснити розв’язок даної задачі. Представник групи пояснює розв`язок задачі біля дошки, всі інші учні записують умови даної задачі і її розв`язок у зошит.

.

 

 

                                           Група «Дослідники»

Завдання 1.

Два теплоходи А і В, які знаходяться у відкритому морі на відстані 20 км один від одного, одночасно отримали сигнал «SOS» із корабля С, який тоне. Радіопеленг по відношенню до ліній АВ на судні А дорівнює 25º, а на судні В 130 º. Хто перший прийде на допомогу, якщо максимальна швидкість судна А 60 км/год, а судна В =55 км/год.

 

 

 

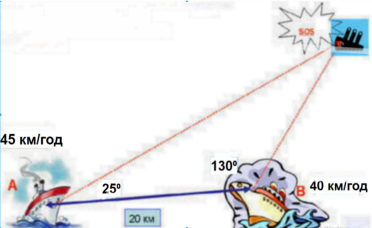
1. Кут С= 180º-155º=25º,  sin130º = sin50º =0,766; sin25º=0,4226.
2. АС = ;  АС = ;  АС 36км.
3. Оскільки кут А дорівнює куту С, то трикутник АВС рівнобедрений, тому АВ=ВС; отже ВС =20км.
4. t= год. =год. = год.;  t=48 хв.
5. t=год. =год.;  t= 30хв.

Відповідь: судно В прийде на  допомогу швидше на 18 хв.

 

Завдання 2.

     Задача з гідроакустики

     Визначення глибини підводної частини об’єкта за допомогою гідроакустики.

Прямо по курсу льодоходу виявлено айсберг. За допомогою ультразвукового ехолота під максимальним кутом 10 градусів визначено підводну точку С на відстані 200 м. Знайти глибину h підводної частини айсберга.

 

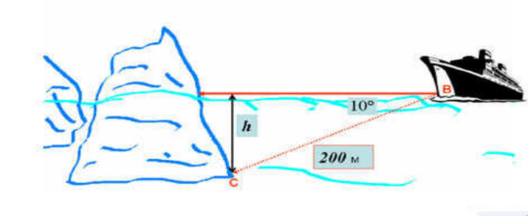
Розв’язання.

h= 200sin10º200·0,1736 34,7(м).

Відповідь: 34,7м.

 

                                      Група «Допитливі»

Завдання 1.

Задача з дефектоскопії

 

Визначення розміру дефекту всередині металевої  деталі великої товщини.

 

При дослідженні металевої деталі методом ультразвукової локації була виявлена всередині тріщина. Знайти довжину тріщини АВ, якщо відстань від межі тріщини до ультразвукового пристрою С дорівнює 50 см і 55 см, а кут АСВ дорівнює 10 градусів.

 

 

 

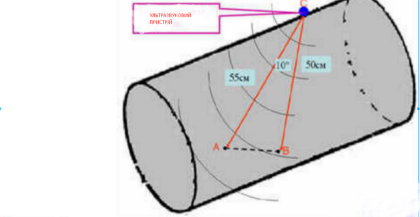
Розв’язання.

За теоремою косинусів:

АВ= АС + ВС- 2·АС·ВС·cos C;

 АВ= 3025+ 2500 - 5500·0,9848 109;

АВ10,4см.

Відповідь: 10,4см.

 

 

 

Завдання 2.

 

 Гори Європи. 

 Вершина гори видна із точки А під кутом, а при наближені до неї на відстань l  м стала видна під кутом . Знайти висоту гори. Обчислити, якщо:

1. кут=58º, кут=60º, відстань l =212,8м. Округлити до одиниць.
2. кут=59º, кут=62º, відстань l =142,42м;

Розв’язання:

 

1. h=; h=4477,7514478(м).
2. h=142,42·;  h2061(м).

Учитель.

Гора висотою 4478м, висоту якої ви знайшли, найпопулярніша у Швейцарії. Біля неї прагнуть побувати туристи, які відвідують Швейцарію. Хто знає назву цієї гори?

  Відповідь: Матерхорн.

 

 

 Гора висотою 2061м сама висока гора  в Карпатах. Яка назва цієї гори?

Відповідь: Говерла.

 

 

                                         Група «Практики»

Завдання1.

 

1). Літак летить горизонтально над рівнем моря на висоті  12км. зі швидкістю 800. Пілот замітив, що кут зниження на вершину гори становить 23º. Через 90 сек. він відмітив, що кут зниження став 78º. Яка висота гори над рівнем моря?

Розв’язання:  90сек.=год.=год.

Нехай літак летить із точки А зі швидкістю 800. За 90 сек. він пролетить відстань АВ= 800·=20(км).  Нехай АК- відстань на якій летить літак над рівнем моря. АК=12км. МД- зображення гори. Точка Д – вершина гори. Продовжимо МД до перетину з променем АВ, дістанемо точку С. Кут СВД- зовнішній кут трикутника АВД. КутАДВ=78º- 23º=55º. За теоремою синусів: =. КутАВД=180º-78º. КутАВД=102º;

Sin102º=sin78º; ВД=;  ВД=; ВД;

 ВД9,5км. Із трикутника ВСД: СД=ВД·sin78º. СД9,5·0,9781; СД9,3км.

 

М Д 12-9,3=2,7(км.)

 

Відповідь: 2,7км.

Завдання 2.

 Будинок шириною 10м. має дах з нахилом 35º з однієї сторони і 41º - з іншої. Знайти довжину скатів покрівлі. Відповідь округлити до десятих.

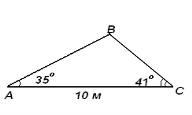Розв’язання: 

Нехай АС=10м., кут А =41º, кутС=35º, тоді кут В=180º-( 35º+41º)=180º-76º=104º. За теоремою синусів: =,BC=, sin104º=sin76º,BC, BC5,9м.

, AB=(м.)

 

Відповідь: 5,9м.; 6,8м.

 

 

                                       Група «Всезнайки»

Завдання 1.

 Будівельники отримали завдання побудувати міст через річку із точки В в точку С. Яка буде довжина мосту, якщо відстань АС дорівнює 100м., кут А в трикутнику АСВ становить  88º, а кут С дорівнює 24º?

Розв’язання.

В = 180º - (88º+24º);  В=  180º -112º= 68º. За теоремою синусів: ;

ВС=; ВС=; ВС;  ВС

         Відповідь: ВС

Завдання 2.

Знайти площу ділянки чотирикутної форми, зображеної на малюнку.

 

 

 

Розв’язання:

       Проведемо діагональ ВД. Отже:

= (21·40·sin115º+23·45·sin55º), sin115º=sin65º0,9063.

       S ·(840·0,9063 + 1035·0,8192)804,6(м).

                                                        Відповідь: 804,6м.

 

 

Підбиття підсумків уроку

Рефлексія

Учитель.

         Ми розглянули декілька прикладів, де потрібні знання з теми « Розв’язування трикутників.» У всіх галузях практичної діяльності людини, навіть у таких традиційно «не математичних», як управління виробництвом, біологія, медицина, лінгвістика, надійно і ефективно працює математика. Вона також працює на колгоспних ланах, будівельних майданчиках, допомагає освоювати космос, і таких прикладів можна назвати безліч.

        Отже, ми переконуємося в тому, що кожному, незалежно від того, де і ким він працюватиме, доводиться користуватися  знаннями з математики. І той, хто свідомо володітиме ними, завжди досягатиме успіху, бо, як писав видатний учений і педагог

В. О. Сухомлинський, «…математика – це насамперед думка допитлива, що бажає все знати, про все мати уявлення. Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер.»

 

Запитання.

1. Що було для вас найцікавішим на уроці і чому?
2. Із якими труднощами ви зіткнулися в процесі розв’язання задач прикладного характеру?
3. Яка роль тригонометричних функцій у вирішенні задач прикладного характеру?
4. Чого ви навчилися під час уроку?
5. Зробіть висновок, яку практичну роль відіграє математика у повсякденному житті людей?

Вчитель: На уроці ви наполегливо працювали, продемонстрували знання, активність, добре мислили.

 

(Оцінювання учнів. Підраховується кількість балів, які кожен учень набрав за урок.)

 

 Домашнє завдання: Самостійно вдома скласти дві задачі, які можна розвязати:

1. за допомогою теореми синусів
2. за допомогою теореми косинусів

 

Таблиця самооцінювання

ПІБучня	Віжповіді на теоретичні запитання (10 або менше)	Усне виконання      вправ (13або менше)	Доповідь учнів          (3)	Письмове виконання вправ              (6)	Усього балів

 

 

                                    Шкала переведення балів в оцінку

Бали	0-5	6-9	10-11	12-15	16-19	20-23	24-27	28-29	30-31	32
Оцінка	3	4	5	6	7	8	9	10	11	12

 

 

 

 

 

 

Використані джерела

1. Мерзляк А.Г., Полонський В.Б.,Якір М.С. Геометрія: підручник для 9 кл. загальноосвіт.навч.закладів–Х.: Гімназія, 2017.–240 с.: іл.
2. Газета для вчителів математики № 20 (752), жовтень 2014.

               3.  Старова О. О. Геометрія. 9 кл. .- Х: Вид. група «Основа», 2009.-144с.-

 (Серія «Мій конспект»).

               4.   3000 задач с ответами по математике. Издательство “Экзамен”, М. 2013.