Застосування технології критичного мислення у власному досвіді (методична розробка)

ЗАСТОСУВАННЯ ТЕХНОЛОГІЇ КРИТИЧНОГО МИСЛЕННЯ У ВЛАСНОМУ ДОСВІДІ

8 клас

Тема уроку: Розв’язування раціональних рівнянь

Мета: навчальна - узагальнити знання про рівняння, продовжувати формувати навички розв’язування раціональних рівнянь (лінійних і дробових), розглянути різні способи їх розв’язування;

розвивальна - розвивати пізнавальний інтерес, формувати уміння правильно й чітко висловлювати свої думки;

виховна - прищеплювати любов до знань, розширювати світогляд.

Тип уроку: формування знань, вмінь і навичок.

Обладнання: картки-сигнали, портрети вчених-математиків, проектор.

Хід уроку

І. Організаційний етап

 Давайте, створимо позитивну ауру в класі: посміхнемося один одному. А я вам бажаю, щоб ці 45 хв. пройшли з користю і цікаво. Тож, починаємо урок.

ІІ. Перевірка домашнього завдання

 Відкрийте зошити і перевірте виконання домашньої роботи у сусіда. Чи є учні, що не виконали домашнього завдання? Чи є проблеми?

ІІІ. Повідомлення мети і плану уроку

 Сьогодні на уроці йтиметься про рівняння.

Рівняння використовували вже близько 4000 років тому для практичних потреб людей. Перші згадки про рівняння вчені знайшли у Вавилоні. Рівняння були відомі китайським, індійським, єгипетським стародавнім вченим. Ще Евклід писав «Рівняння ─ мова алгебри». Сучасну символіку, запис, формули і саме розв’язування рівнянь ми маємо завдяки вченим Західної Європи – Ф. Вієту, Р. Декарту, Л. Ейлеру, І. Ньютону та ряду інших вчених.

 На уроці ми систематизуємо знання про рівняння, удосконалимо вміння розв’язувати дробові раціональні рівняння та складати рівняння за текстом задачі.

ІV. Актуалізація опорних знань

Прийом « Мікрофон» (фронтальне опитування учнів):

1. Що називають рівнянням?
2. Що називають коренем рівняння?
3. Що означає розв’язати рівняння?
4. Скільки коренів може мати рівняння?
5. Встановіть відповідність між рівняннями та їх розв’язками (проектується)

Рівняння:        Корені:

1.  (х-3) (х+8) = 0       А) жодного;
2. = 0        Б)  -10;                                                                                                                                 В)  3;  -8;
3. 2х+3 = −17        Г)  -3;  8;
4.   +19 = 9      Ґ)  5;
5. = 0        Д)  6;  -6;

          Е)  6

6) Які рівняння називаються рівносильними?

7) Гра « Вірю, не вірю»(за допомогою сигнальних карток▲ – ні,● – так ), завдання проектуються.

Чи вірите ви,що пара рівнянь є рівносильними?

А)   2х−4 = 9    і   2х = 5

Б)    3х+1 = 5  і  3х = −6

В)   7х + 9 = х −1 і  6х = −10

Г)   + 9 = 0  і   = −2

8) Які види рівнянь ми вже розв’язували?

(Лінійні або ті, що зводились до них та познайомились з дробово-раціональними)

V. Удосконалення знань і вмінь

Прокоментувати алгоритм розв’язування рівнянь та розв’язати їх самостійно ( рівняння проектуються):

  Варіант 1     Варіант 2

 (х - 6) – (2х – 9) = − 12    100: (6х – 5 ) = 4

 х – 6 – 2х +9 = − 12    6 х – 5 = 100 : 4

• х = − 15      6 х− 5 = 25

х = 15       6 х = 30

         х = 5

Відповідь : 15      Відповідь :  5

• Яке рівняння називають дробово-раціональним? (Якщо у раціональному рівнянні хоча б одна частина є дробовим

 виразом , то воно називається дробово-раціональним)

- До якої системи слід перейти, розв’язуючи рівняння ви= 0  (наприклад: 

─ Чи є дані рівняння дробово-раціональними ? (Двоє учнів розв’язують біля дошки, інші − працюють у зошитах)

  Варіант 1      Варіант 2

   + = 2      + =

  Відповідь: 4       Відповідь: 8

− Як можна раціонально розв’язати таке дробове рівняння (один з учнів розв’язує біля дошки)?

        =  

Відповідь :

А зараз ускладнимо собі завдання і розв’яжемо дробове рівняння, що містить модуль.

Один  учень одержує завдання на карточці і працює біля дошки.

Колективне розв’язування:

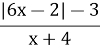  = 0

 Відповідь: −; .

Мало навчитися лише розв’язувати рівняння, набагато цікавіше і складніше навчитися їх складати самим.

Ще Ньютон у своєму підручнику «Загальна арифметика» писав, щоб розв’язати текстову задачу, досить перекласти її з рідної мови  на мову алгебраїчну.

Зробимо це на прикладі текстової  задачі про життя давньогрецького математика Діофанта, про якого не так багато відомо, але він залишив слід в алгебрі своїми відомими діофантовими рівняннями. Текст задачі взято з епітафії на його могилі.

Задача (проектується на екран)

«Подорожній! Прах Діофанта гробниця ховає : вдивися і камінь Мудрим мистецтвом розкриє покійного вік.

З волі богів шосту частину життя був він дитина,

А ще половину шостої – стрів із пушком на щоках.

Тільки минула сьома , з коханою він одружився,

З нею п'ять років проживши, сина діждався мудрець.

Та півжиття свого тішився батько лиш сином :

Рано могила дитину у батька забрала.

Років двічі по два батько оплакував сина. 

А по роках цих і сам стрів він кінець свій печальний…»

Працюєте у парах. Яка пара упорається швидше? ( гра « Двоє як один» )

х + х + 5 +  х + 4 = х  (× 84)

14х + 7х +12х +420 + 42х + 336 -84х = 0

• 9х = −756

х = 84 (роки)

Відповідь : 84 роки

VII. Підсумки уроку

 Ми повторили та узагальнили знання про  рівняння, переконалися, що  багато видатних математиків присвятили їм своє життя. Пам’ятайте, що більшість реальних процесів можна записати рівнянням.

 В зошиті зробіть самооцінку своїх знань та вмінь на уроці.

Наприклад :

Я знаю ☺

Я вмію ☺ 

Усе зможу ☺ 

Учні здають зошити на перевірку. При оцінюванні враховуватиметься робота на уроці і в зошиті.