Завдання для програмового навчання з алгебри та початків аналізу в 10 класі по темі "Похідна"

Завдання для програмового навчання з алгебри та початків аналізу

в 10 класі по темі: „Похідна”

Завдання Ι-1-1

1.Використовуючи означення похідної знайти похідні наступних функцій:

     а) y =3 x+4. Знайти                                                                                                                             

     б) y =+5. Знайти          

                                                       Розв’язання

а) Відомо, що  при .

Знайдемо похідну функції по наступному алгоритму.

1) y( ... +4

2)

3)               при  .

Так як    не залежить від , то        

  б)y=. Знайти

 Відомо що     .

Знаходимо похідну функції  в точці за наступним алгоритмом:

1) y (-2+ =(     )  … -4… +5

2)  …                                     

3)

при. Тоді,

1) y (-2,5+(     )

2)

3)

при  . Тоді,

Завдання  - І-1-2

1.Знайдіть похідну функції:

a) x;    б)2x;      в)x;       г)5x .

                                            Розв’язання

Відомо, що для будь якого цілого n і будь якого x( x  ≠ 0 при n≤1)   (x  

а) (x

б) (2x

в) (x

г) (5x

2.Знайдіть похідну функції:

а) 3; б) 5 в ); г ).

                                                 Розв’язання

1. Відомо, що.

 Наприклад,  ; .

2. За означенням степеня з від’ємним показником  x; Наприклад .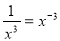

а) (3

б) (2x

в)

г)(

3.    Знайдіть похідну функцій:

a)5x б)3x; в).

                                Розв ‘язання

1. Відомо, що(x
2. За означенням степеня з від‘ємним показником  x;

Похідна суми рівн сумі похідних

a)(5x

б)(3x

в)(

Завдання-I-1-3

1. Знайдіть похідну функції:

а) (2x+1); б) (1-3x)

                                Розв’язок:

1)Відомо, що похідна добутку знаходиться за формулою

2)

3)Похідна суми дорівнює сумі похідних

а)

                б)2.Знайдіть похідну функції:

      а); б); в);г)

      1)Відомо, що похідна частки знаходиться за формулою

      2) ;

       а)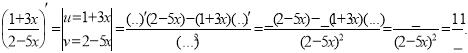

      б)

 в)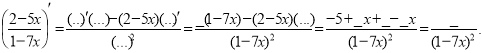

 г)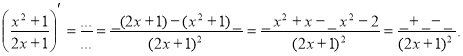

Завдання-I-1-4

1. Знайдіть область визначення функції:

а) ; б) в)

                                Розв’язок:

1. Відомо, що 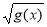визначений при
2. Дріб 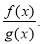має зміст при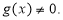
3.  

а)

D(y):

                     

    .

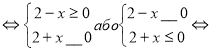
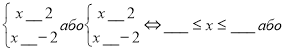Відповідь:  ___; ___ .

б)                                                        

D(y):

                          

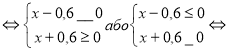
x ____ __   або  x ____ __

                           

Відповідь: ( ___; ___    ___; ___ ) .

в)

Так як стоїть в знаменнику дробу,то D(y):

                                                                                                    

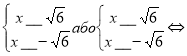
_________  або ___  x  ___

Відповідь: ( ___ ; ___)  ( ___ ; ___).

2.  Знайти похідну функції:

     a) xcosx;   б)    в)

Розв’язання

а) Похідна функції обчислюється за формулою: 

·_.

б) - складена функція, похідна складеної функції h(x) обчислюється за формулою: ·

,¯,    f(x)=sinx.

¯, 

¯·_=_sin¯x·_

в)  Похідна суми рівна сумі похідних: 

Завдання І-2-1

1. Знайдіть тангенс кута нахилу дотичної до графіка функції f  в даній точці

а)   М(-2;-8);   

б) 

Розв’язання

Відомо, що де - абсциса точки дотику.

а)

б)

   (3x¯¯

       Напишіть рівняння дотичної до графіка функції  f  в точках з даною абсцисою:

a)

б)

Розв’язання

Відомо, що рівняння дотичної таке:

або

Щоб написати рівняння дотичної до кривої в точці з абсцисою потрібно:

1. Обчислити
2. Знайти 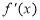і обчислити її значення в точці , тобто
3. Підставити знайдені числа у рівняння (1)

а)

y=2+__(x+1).

б)

    ¯   ¯=__