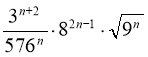Завдання І етапу Всеукраїнської учнівської олімпіади з математики

№

Зміст завдання

Бали

1.

Сума двох чисел 462. Одне з них закінчується нулем. Якщо цей нуль закреслити, то одержимо друге число. Знайти ці числа.

5

2.

В одному дворі живуть четверо юнаків. Відомо, що Вадим і водій старші за Сергія, Микола і сантехнік захоплюються плаванням, бібліотекар – молодший із юнаків. Антон і перукар грають в доміно проти Сергія і бібліотекаря. Визначити професії юнаків.

5

3.

Довжина прямокутного поля 80м, а площа цього поля дорівнює 3200. Знайти довжину іншого прямокутного поля площа і ширина якого у 2 рази менші, ніж першого поля.

5

4.

У їдальню привезли рибу: коропи, сазани, судак і лящі. Коропів було 46кг, сазанів було 30кг,  а судаків було у 3 рази більше, ніж лящів. Коли половину риби витратили, то залишилось 90кг. Скільки судаків привезли у їдальню?

5

5.

800 грн.  можна обміняти на 100 дукатів, а 100грн. можна обміняти на 250 талярів.   На скільки дукатів можна обміняти 100 талярів?

5

№

Зміст завдання

Бали

1.

Знайти значення виразу    , якщо    = 20

5

2.

Дівчинка розрізає квадратний лист паперу з периметром 20см на два прямокутники. Периметр одного такого прямокутника дорівнює 16см. Знайти периметр другого прямокутника.

5

3.

Онуку стільки місяців, скільки років дідусеві.  Дідусь з онуком мають разом 91 рік. Скільки років дідусеві і скільки років онуку?

5

4.

Знайти наступне число у числовому ряді 

6; 8; 16; 18; 36 …

5

5.

Середнє арифметичне деяких 10 чисел дорівнює 14. Якщо чотири числа видалити з даного набору чисел, то середнє арифметичне тих чисел, що залишилися буде дорівнювати 11. чому дорівнює середнє арифметичне видалених чисел?

5

№

Зміст завдання

Бали

1.

Відомо, що  = .  Знайти 

5

2.

Знайти 15%   від 

5

3.

Кіт  Матроскін  вирішив покрити підлогу квадратної форми квадратними плитками. Спочатку він виклав плитку по краю підлоги і на це у нього пішло 84 плитки. Скільки всього  Матроскіну треба мати плиток, щоб покрити всю підлогу?

5

4.

У трикутнику АВС   А більший від С на 30°. Точка К лежить на АС так, що АВ = ВК. Знайти  КВС.

5

5.

Знайти наступне число у числовому ряді 

3;  5;  9; 17;  33…

5

№

Зміст завдання

Бали

1.

Відомо, що  + = .  

Знайти  n

5

2.

Точки А, В, С, D ділять коло на дуги так, що

 АВ : ВС : СD : АD = 2 : 3 : 5 : 8. Знайти кут між прямими АВ і СD.

5

3.

Відомо, що х + у + z = 150;   x: у = 2 : 3;  у : z = 2 : 5.

Знайти х,у, z

5

4.

Порівняти

5

5.

Побудувати графік функції: 

у =

5

№

Зміст завдання

Бали

1.

Число ( с + 2 ) ділиться на 5. Довести, що число (3с + 16) також ділиться на 5

5

2.

Визначити,  на скільки відсотків збільшиться площа квадрата, якщо його периметр збільшиться на 10%.

5

3.

Побудувати графік функції :

у =

5

4.

В прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки 5 см і 12 см. Знайти площу трикутника.

5

5.

Середнє арифметичне п’яти чисел дорівнює 200. Одне з цих чисел дорівнює 400. Знайти середнє арифметичне решти чотирьох чисел.

5

№

Зміст завдання

Бали

1.

Побудувати графік функції:

5

2.

В трикутнику АВС бісектриси кутів В і С перетинаються під кутом 132°. Знайти величину кута А.

5

3.

Спростити:

5

4.

Розв’язати рівняння:

5

5.

На скільки відсотків збільшиться площа прямокутника, якщо довжину збільшити на 20%, а ширину – на 10%.

5