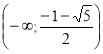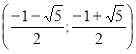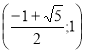Завдання з теми "Рівняння з параметрами"
І. Передмова
Розв’язати рівняння з параметрами означає знайти всі його розв’язки для кожної системи допустимих значень параметрів. Значення параметрів, при переході через які відбуваються якісні зміни рівняння, називаються контрольними значеннями параметрів.
При розв’язуванні рівнянь з параметрами область зміни параметрів може бути заданою, або в рівнянні вказано додаткові умови, наприклад, знайти значення рівняння, при яких корінь рівняння задовольняє задану рівність, нерівність і т.д. Якщо не вказані умови для параметрів, то вважається, що параметри набувають усіх своїх допустимих значень.
ІІ. Лінійні рівняння з однією змінною
Рівняння виду ах=в, де а і в – дійсні числа, х – змінна, називаються лінійними рівнями з однією змінною. Дослідимо його.
- Якщо a = 0 і в =0, тобто 0х= 0. Це рівняння задовольняє будь-яке дійсне значення (х є R), а тому воно має безліч розв’язків.
-
Якщо a = 0 і в ≠ 0, то рівняння не має розв’язків. (х
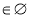 ).
).
-
Якщо a≠0, то рівняння має єдиний розв’язок х =

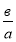 .
.
Приклад 1. Розв’язати рівняння х+2=ах.
Розв’язання.
(1-а)х = -2; (а-1)х = 2
1.Якщо а=1, то ох=2, х![]() 2.Якщо а≠1, то х=
2.Якщо а≠1, то х=![]()
Відповідь: Якщо а=1, то х![]() ; якщо а≠1, то х=
; якщо а≠1, то х=![]()
Приклад 2. Розв’язати рівняння (а-1)(а+1)х = (2а+3)(а-1).
Розв’язання
а=1, а= -1 – контрольні значення параметра.
1. якщо а=1, то ох=о, х є R.
2. Якщо а= -1, то ох= -2, х ![]() .
.
3.Якщо а≠1; а≠ -1, то х=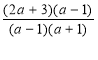 ; х=
; х=![]()
Відповідь: Якщо а=1, то х є R; якщо а= -1, то х ![]() ; якщо а≠1; а≠ -1, то х=
; якщо а≠1; а≠ -1, то х=![]() .
.
Приклад 3. Розв’язати рівняння (а![]() -1)х= а
-1)х= а![]() +а-2.
+а-2.
Розв’язання.
а=1, а= -1 – контрольні значення параметра.
1.Якщо а=1, то ох=о, х є R
2.Якщо а= -1, то ох= -2, х![]() .
.
3. Якщо а≠1; а≠ -1, то х=![]() ; х=
; х=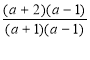 ; х=
; х=![]()
Відповідь: Якщо а=1, то х є R; якщо а= -1, то х ![]() ; якщо а≠1; а≠ -1, то х=
; якщо а≠1; а≠ -1, то х=![]()
Приклад 4. Розв’язати рівняння ![]()
Розв’язання
а≠о.
2(а+1)х=7+3а(х+1); (2а+2-3а)х=3а+7; (2-а)х=3а+7
1. якщо а=2, то ох=13, х ![]() .
.
2. якщо а≠2 і а≠ о, то х=![]() .
.
Відповідь: Якщо а=0 або а=2, то х ![]() ;
;
якщо а≠2 і а≠ о, то х=![]() .
.
Завдання для самостійного розв’язання.
- Розв’язати рівняння ах-3=a.
- Розв’язати рівняння (a-1)(a+1)x-a-1=0.
- Розв’язати рівняння (a+4)x-2,5x=(a-2)(a+3)+3,5x.
- Розв’язати рівняння 7,5x-2ax-a2=5,5x-3ax-4.
- Розв’язати рівняння (a2-1)x=a+1.
- Розв’язати рівняння (a2-1)x=a2+3a-4.
-
Розв’язати рівняння
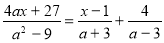 .
.
- При яких значеннях параметра а рівняння 2(х-1)=5+ах має корінь, більший за 1?
- При якому значенні параметра k рівняння k+2х=2(х-3) не матиме коренів?
- При яких значеннях параметра а корінь рівняння х+а=ах+а2 від’ємний?
- Знайдіть усі значення параметра а, при кожному з яких рівняння 10х-15а=13-5ах+2а має корінь, більший ніж 2.
- Визначте, при яких значеннях а рівняння (х-1)(а-2)=1 має корінь, який належить проміжку (1;2).
ІІІ.Квдратні рівняння з однією змінною
Рівняння виду ![]() + вх + с = о, де а, в, с – дійсні числа і а≠ о, називаються квадратними. При розв’язанні таких рівнянь з параметрами розглядають випадки:
+ вх + с = о, де а, в, с – дійсні числа і а≠ о, називаються квадратними. При розв’язанні таких рівнянь з параметрами розглядають випадки:
1. якщо а=о, то рівняння є лінійним вх + с = о.
2. Якщо а≠ о, то знаходимо D= ![]() .
.
А) Якщо D<0, то х![]() .
.
Б) Якщо D≥0, то х=![]() .
.
Приклад 1. Розв’язати рівняння ![]() +(а-2)х+а+1=0.
+(а-2)х+а+1=0.
Розв’язання.
D=(а-2)![]() -4(а+1)=
-4(а+1)= ![]() -4а+4-4а-4=
-4а+4-4а-4=![]() -8а.
-8а.
1.Якщо D<0, тобто ![]() -8а<0, а(а-8) <0, а є (о;8), то х
-8а<0, а(а-8) <0, а є (о;8), то х ![]() .
.
2.Якщо D≥0, тобто ![]() -8а≥0, а(а-8) ≥0, а є (-∞;о]U[8;+∞), то х1,2=
-8а≥0, а(а-8) ≥0, а є (-∞;о]U[8;+∞), то х1,2=![]() .
.
Відповідь. Якщо а є (0;8), то х![]() ;
;
якщо а є (-∞;о]U[8;+∞), то х1,2=![]() .
.
Приклад 2. Розв’язати рівняння (а-1) ![]() +2(2а+1)х+4а+3=0
+2(2а+1)х+4а+3=0
Розв’язання.
1. Якщо а=1, то 6х=-7, х=-![]() .
.
2. Якщо а≠ 1, то D![]() = (2а+1)
= (2а+1)![]() -(а-1)(4а+3)=4а
-(а-1)(4а+3)=4а![]() .
.
А) Якщо 5а+4<0, тобто а<-![]() , то х
, то х![]() .
.
Б) Якщо 5а+4≥0, тобто а ≥-![]() , то х=
, то х=![]() .
.
Відповідь. Якщо а=1, то х=-![]() ;
;
якщо а є (-∞;-![]() ), то х є ø;
), то х є ø;
якщо а є [-![]() ;1)U(1; +∞), то х=
;1)U(1; +∞), то х=![]() .
.
Приклад. 3 Розв’язати рівняння а(а+1) х![]() -(
-(![]() )х+а(а-1)=0.
)х+а(а-1)=0.
Розв’язання.
1. а=о і а= -1- контрольні значення параметра.
Якщо а=о, то х=о.
Якщо а=-1, то –х +2=0; х=2.
2.а≠о і а≠-1, то D= ![]()
х=![]() ; х
; х![]() =
=![]() =
=![]() ; х
; х![]() =
=![]() =
=![]() .
.
Відповідь. Якщо а=о, то х=о;
якщо а=-1, то х=2;
якщо а≠о, а≠-1, то х![]() =
=![]() ; х
; х![]() =
= ![]() .
.
Приклад 4. Розв’язати рівняння (![]() .
.
Розв’язання.
1. ![]() а=-2 і а=1 – контрольні значення параметра.
а=-2 і а=1 – контрольні значення параметра.
Якщо а=-2, то 9х=-3, х=-![]() .
.
Якщо а=1, то 6х=0, х=0.
2.Якщо а≠-2, а≠1, то 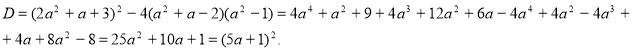
D≥0; тому х=![]()
![]()
=-![]()
![]()
Відповідь. Якщо а=-2, то х=-![]() ; якщо а=1, то х=0; якщо а≠-2, а≠1, то
; якщо а=1, то х=0; якщо а≠-2, а≠1, то ![]()
![]()
![]()
Розв’яжемо дробово-раціональні рівняння з параметрами. Як і розв’язання відповідних рівнянь без параметрів, розпочинати потрібно із знаходження ОДЗ рівняння.
Після перенесення доданків в ліву частину рівняння, зведення до спільного значення, прирівнюємо чисельник отриманого дробу до нуля. Отримавши лінійне або квадратне рівняння, розв’язуємо його. В кінці обов'язково потрібно встановити, при яких значеннях параметрів знайдені розв'язки належать ОДЗ рівняння.
Приклад 1. Розв'язати рівняння ![]()
Розв’язання.
ОДЗ х≠2а
![]()
![]()
D=(![]() >0, х=
>0, х=![]() ; х
; х![]() =а+1; х
=а+1; х![]() =а-2.
=а-2.
Знайдемо, ті значення параметра а, при яких х![]() не є коренем рівняння.
не є коренем рівняння.
а+1=2а;а=1.При цьому значенні параметра рівняння матиме тільки один розв’язок х=1-2=-1.
Знайдемо, ті значення параметра а, при яких х![]() не є коренем рівняння. а-2=2а; а=-2.
не є коренем рівняння. а-2=2а; а=-2.
Якщо а=-2, то рівняння матиме тільки один корінь х=-2+1=-1.
Відповідь. Якщо а=1 або а=-2. то х=-1; якщо а≠1 і а≠-2, то х![]() =а+1, х
=а+1, х![]() =а-2.
=а-2.
Приклад 2. Розв’язати рівняння. ![]()
Розв’язання. ОДЗ х≠1.
![]()
![]()
1. Якщо а=0, то –х+1=0, х=1 – не належить ОДЗ рівняння.
2. Якщо а≠0, то рівняння квадратне.
Знайдемо D. D=(а+1)![]()
х=![]()
![]()
х![]() =
=![]()
Знайдемо значення параметра а, при яких х![]() не є коренем рівняння. а+1; а=о, тоді х
не є коренем рівняння. а+1; а=о, тоді х ![]() .
.
Знайдемо значення параметра а, при яких х![]() не є коренем рівняння.
не є коренем рівняння. ![]() а=-1, а
а=-1, а![]() .
.
Відповідь. Якщо а=о, то х![]() ; якщо а≠0, то х
; якщо а≠0, то х![]() =а+1, х
=а+1, х![]() =.
=. ![]() .
.
Приклад 3. Розв’язати рівняння ![]()
Розв’язання. ОДЗ ![]()
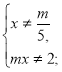
![]() ;
; ![]()
1. 10![]() -15=0,
-15=0, ![]() =1,5 – контрольне значення; якщо
=1,5 – контрольне значення; якщо ![]() =1,5, то ох=15,5, х
=1,5, то ох=15,5, х![]() .
.
2. Якщо ![]() ≠1,5, то х=
≠1,5, то х=![]()
Знайдемо значення ![]() , при яких х=
, при яких х=![]() є коренем даного рівняння.
є коренем даного рівняння.
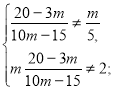
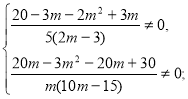
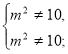
![]()
Відповідь. Якщо ![]() то х
то х ![]() , якщо
, якщо ![]()
![]()
![]() то х=
то х=![]() .
.
Приклад4. Розв’язати рівняння ![]()
Розв’язування.
ОДЗ. х≠2, ![]()
![]()
(![]()
![]()
1. ![]() контрольне значення параметра. Якщо
контрольне значення параметра. Якщо ![]() то -9х=0, х=0.
то -9х=0, х=0.
2. ![]()
D= ![]()
![]()
![]()
х=![]()
![]()
х![]() =
=![]()
Знайдемо значення ![]() , при яких х
, при яких х![]() не є коренем рівняння.
не є коренем рівняння.
![]()
![]()
![]()
Якщо ![]() =4, то рівняння матиме один розв’язок х=
=4, то рівняння матиме один розв’язок х=![]()
Знайдемо значення ![]() , при яких х
, при яких х![]() не є коренем рівняння.
не є коренем рівняння. ![]()
![]()
![]()
Якщо ![]() то рівняння має один розв’язок х=
то рівняння має один розв’язок х=![]()
Відповідь. Якщо ![]() =1,
=1, ![]() = -1, то х
= -1, то х ![]() ; якщо
; якщо ![]() = -2, то х=0; якщо
= -2, то х=0; якщо ![]() = -5,
= -5, ![]() =4, то х=
=4, то х=![]() ;
;
якщо ![]() ≠1,
≠1, ![]() ≠ -1,
≠ -1, ![]() ≠ -2,
≠ -2, ![]() ≠ -5,
≠ -5, ![]() ≠4, то х
≠4, то х![]() =
=![]() х
х![]() =
=![]()
Приклад 5. Розв’язати рівняння ![]()
Розв’язання.
ОДЗ. ![]()
![]() ≠0.
≠0. ![]()
![]()
D=![]() >0,
>0,
х=![]() то х
то х![]() =
=![]() х
х![]() =
=![]()
Знайдемо значення параметра ![]() , при яких х
, при яких х![]() є коренем рівняння.
є коренем рівняння.
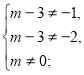
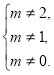
Якщо ![]() =2, то рівняння має розв’язок х=2+1=3.
=2, то рівняння має розв’язок х=2+1=3.
Якщо ![]() =1, то рівняння має розв’язок х=1+1=2.
=1, то рівняння має розв’язок х=1+1=2.
Відповідь. Якщо ![]() = -2, то х=-5; якщо
= -2, то х=-5; якщо ![]() =-3, то х=-6; якщо
=-3, то х=-6; якщо ![]() =2, то х=3; якщо
=2, то х=3; якщо ![]() =1, то х=2; якщо
=1, то х=2; якщо ![]() =0, то х є ø; якщо
=0, то х є ø; якщо ![]() ≠-2,
≠-2, ![]() ≠-3,
≠-3, ![]() ≠2,
≠2, ![]() ≠1,
≠1, ![]() ≠0, то х
≠0, то х![]() =
=![]() +1, х
+1, х![]() =
=![]() -3.
-3.
Приклад 6. При яких значеннях параметра а, рівняння має єдиний корінь? Знайти цей корінь. ![]() .
.
Розв’язання.
ОДЗ. х≠±2.>
1. ![]()
D=0, D=![]()
![]() ; х=
; х=![]()
2. D>0, х![]() =2 або х
=2 або х![]() =-2 або х
=-2 або х![]() =2 або х
=2 або х![]() =-2.
=-2.
![]() >0;
>0; ![]() >0; (а
>0; (а![]() ( а
( а![]() >0; а є (- ∞;
>0; а є (- ∞; ![]() U(
U(![]() )
)
х=![]()
А) ![]() 2;
2; ![]() =2+а
=2+а
![]()
 а= -
а= -![]() х=-(
х=-(![]() )
)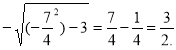
Б) –а+![]() =-2;
=-2; ![]() =а-2
=а-2
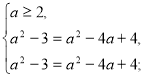 а=
а=![]() х=-
х=-![]() +
+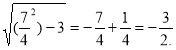
В) –а-![]() =2;
=2; ![]() =-а-2
=-а-2
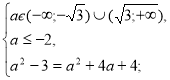
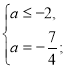 а
а ![]() .
.
4) –а-![]() =-2;
=-2; ![]() =2-а
=2-а
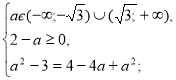 а=
а=![]()
Відповідь. якщо а=-![]() , то х=
, то х=![]() якщо а=
якщо а=![]() , то х=
, то х= ![]() якщо а=
якщо а=![]() то х=
то х=![]() якщо а=-
якщо а=-![]() то х=
то х=![]()
Виділимо основні типи задач, пов’язані із розташуванням коренів х![]() , х
, х![]() квадратного рівняння ах
квадратного рівняння ах![]() відносно числа
відносно числа ![]() R.
R.
Нехайƒ(х)=ах![]() D=
D=![]() тоді:
тоді:
1. ![]() <
< 2.
2.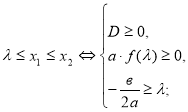
3. ![]() <
<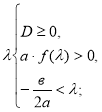
![]() 4.
4. ![]()
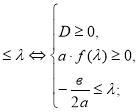
5.![]()
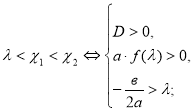 6.
6.![]()
![]()
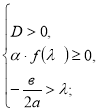 7.
7.![]()
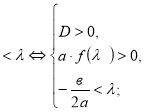 8.
8. 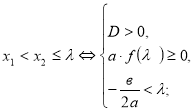
9.![]()
![]() 10.
10. ![]()
Приклад 1.
При яких значення к корені рівняння ![]() будуть більші ніж – 1.
будуть більші ніж – 1.
Розв’язання.
-1<х![]() ≤ х
≤ х![]() .
.
![]()
![]()
![]()
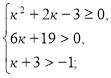
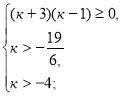
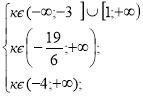 k є
k є ![]()
Відповідь. k є ![]()
Приклад 2.При яких значеннях к рівняння ![]() має корені менші ніж 1.
має корені менші ніж 1.
Розв’язання.
![]()
![]()
![]()
![]()
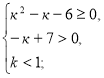
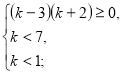
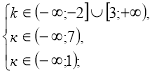 к є
к є ![]()
Відповідь. к є ![]() .
.
Приклад 3. При яких значеннях а число 1 знаходиться між коренями рівняння (2а+1)х![]()
Розв’язання.
![]() ƒ(1)=2а+1-а+а-2=2а-1. (2а+1)(2а-1)<0,
ƒ(1)=2а+1-а+а-2=2а-1. (2а+1)(2а-1)<0, ![]() <0, а є (-
<0, а є (-![]()
Відповідь. а є (-![]()
Приклад 4.При яких значеннях а корені рівняння![]() містяться між числами 0 і 1.
містяться між числами 0 і 1.
Розв’язання. ![]()
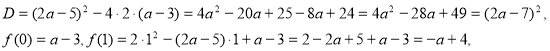
![]()
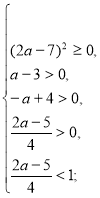
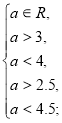 а є (3;4).
а є (3;4).
Відповідь: а є (3;4).
Приклад 5. Знайти всі значення параметра а, при кожному з яких корені рівняння належить вказаній множині. ![]()
Розв’язання.
D=![]() -
-![]()
![]()
![]()

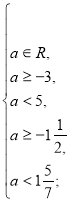
![]()
Відповідь. ![]()
Приклад 6. Знайти всі значення параметра а, при кожному з яких корені рівняння належать вказаній множині. ![]()
Розв’язання.
![]()
![]()
![]()
![]()
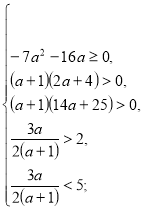
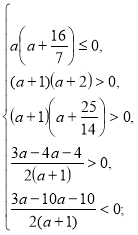
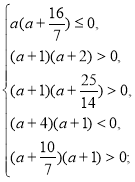
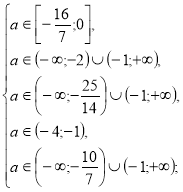
![]()
Відповідь. ![]()
До азбуки квадратного тричлена відноситься і теорема Вієта.
Для того, щоб ![]() і
і ![]() були коренями квадратного тричлена необхідно і достатньо виконати рівностей
були коренями квадратного тричлена необхідно і достатньо виконати рівностей ![]()
Приклад 1.При яких значеннях к корені рівняння ![]() відноситься як 1:4
відноситься як 1:4
Розв’язання. D=![]()
![]() к
к![]()
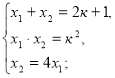
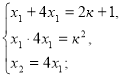
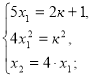
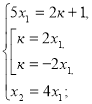
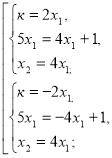
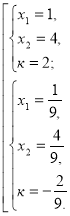 Відповідь. 2; -
Відповідь. 2; -![]()
Приклад 2. ![]() і
і ![]() - корені рівняння х
- корені рівняння х![]()
Знайти таке а, щоб величина виразу ![]() була найменшою.
була найменшою.
Розв’язання.
![]() за теоремою Вієта
за теоремою Вієта ![]() +
+ ![]() =а;
=а; ![]() .
. ![]() = а-1.
= а-1.
Тому ![]()
отже, найменше значення виразу ![]() дорівнює 1 при а=1.
дорівнює 1 при а=1.
Відповідь. 1.
Приклад 3. Корені ![]() і
і ![]() рівняння х
рівняння х![]() задовольняють умову
задовольняють умову ![]() -
- ![]() =1.
=1.
Знайти р при умові, що р>0.
Розв’язання.
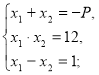
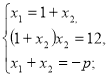
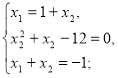
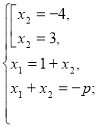

Відповідь. 7.
Приклад 4.
Нехай ![]() і
і ![]() - корені рівняння х
- корені рівняння х![]() де а є N. Обчислити при якому найменшому значені а вираз
де а є N. Обчислити при якому найменшому значені а вираз ![]() ділиться на 25.
ділиться на 25.
Розв’язування.
Отримаємо формулу для оцінки суми п’ятих степенів двох виразів.
![]()
![]()
![]()
Отже, ![]()
За теоремою Вієта ![]() +
+ ![]() =а,
=а, ![]() ·
· ![]() =1.
=1.
![]() =
=![]()
якщо а=1,2,3,4, то ![]() на ділиться на 5. Тому найменше значення а, при якому
на ділиться на 5. Тому найменше значення а, при якому ![]() дорівнює 5.
дорівнює 5.
Відповідь. 5.
Якщо ![]() корені рівняння
корені рівняння ![]() то мають місце співвідношення:
то мають місце співвідношення:
![]()
![]()
![]()
+![]() d;
d; ![]() які називаються формулами Вієта.
які називаються формулами Вієта.
Покажемо, як використовується властивості коренів рівнянь четвертного степеня при розв’язуванні рівнянь з параметрами.
Приклад 5.
При якому к>0 корені рівняння ![]() утворюють арифметичну прогресію?
утворюють арифметичну прогресію?
Розв’язання.
Нехай рівняння має чотири корені: ![]()
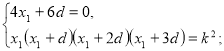
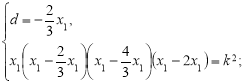
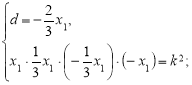
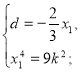
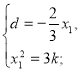 оскільки,
оскільки, ![]() - корінь рівняння, то підставляємо отримане значення в дане рівняння.
- корінь рівняння, то підставляємо отримане значення в дане рівняння.
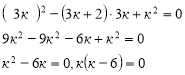
к=0 або к=6.
Відповідь. 6.
Розв’яжемо рівняння з параметрами, які містять змінну під знаком модуля.
Приклад 1.
Знайти значення а, при яких рівняння має один корінь.
![]()
Розв’язання.
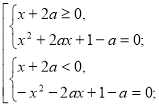
І. Розглянемо першу систему сукупності (І) ![]()
D![]()
а) Якщо ![]() то рівняння має один корінь.
то рівняння має один корінь.
![]()
![]() х=-а
х=-а
Перевіряємо виконання умови х![]()
а=![]() ;-а
;-а![]()
![]() отже, при а=
отже, при а=![]() дане рівняння не має розв’язків.
дане рівняння не має розв’язків.
б) Якщо ![]() і для одного з коренів не виконується умова
і для одного з коренів не виконується умова ![]() .
.
1) 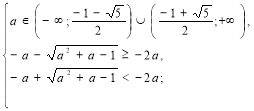
Розв’яжемо окремо ірраціональні нерівності даної системи.
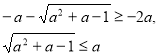
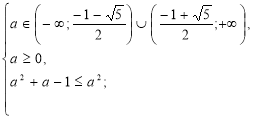
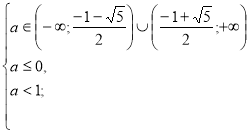
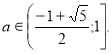
![]()
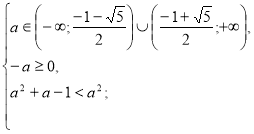
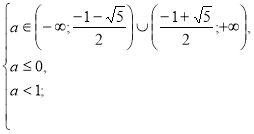
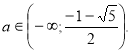
Повертаємося до системи (1).
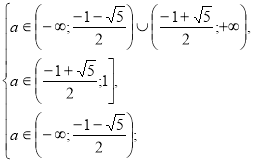 а
а ![]() .
.
2) 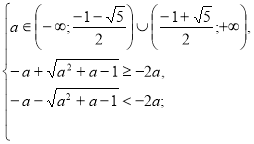
Розв’яжемо окремо ірраціональні нерівності системи. ![]() ,
, ![]()
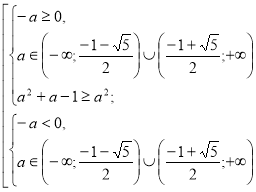
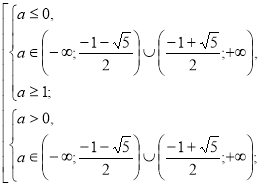
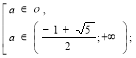
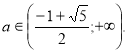
![]()
![]()
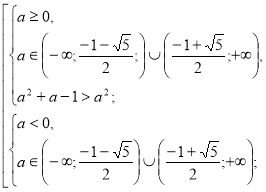
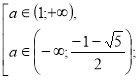
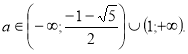
Повертаємося до системи (2).
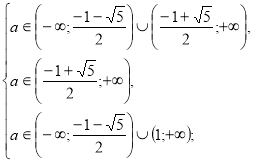
![]()
ІІ. Розв’яжемо другу систему сукупності (ІІ).
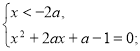
а) ![]() a є ø.
a є ø.
б) ![]() при будь-якому а.
при будь-якому а.
![]()
Розглянемо два випадки, коли один з коренів не задовольняє умову х<-2a.
1) 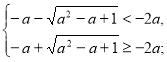
Розв’яжемо окремо кожну з ірраціональних нерівностей системи.
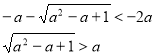
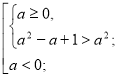
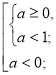
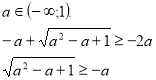
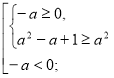
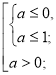 а є R.
а є R.
Повернемося до системи (1).
![]() а є (-∞;1).
а є (-∞;1).
2) 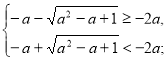
Розв’яжемо окремо кожну з нерівностей даної системи.
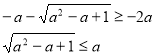
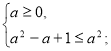
![]()
![]()
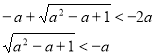
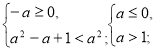 а є Ø.
а є Ø.
Отже, повертаємося до систему (2)
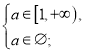 а є Ø.
а є Ø.
Щоб встановити значення параметра а, при яких дане рівняння має єдиний розв’язок, знайдемо те значення а при яких система (І) та (ІІ) мають по два розв’язки.
Система (І) має дав розв’язки D>0 і корені задовольняють умову х≥-2а.
(А)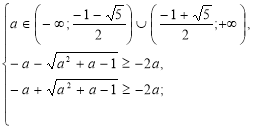
Випишемо та розв’яжемо ірраціональні нерівності системи.
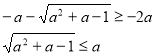
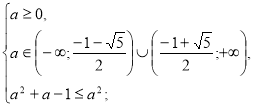
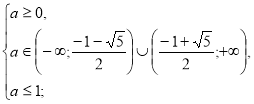
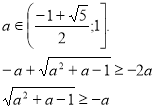
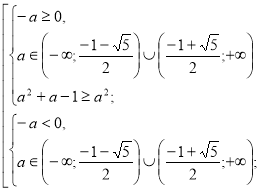
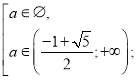
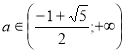
Повертаємося до системи (А).
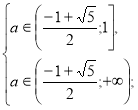
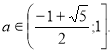 .
.
(Б)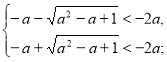
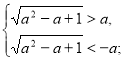
![]()
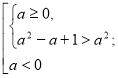
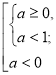
![]()
![]()
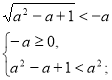
![]() а є ø.
а є ø.
Отже, система (Б) має вигляд;
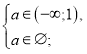 а є ø.
а є ø.
Внесемо в таблицю дані про кількість розв’язків рівняння в залежності від параметра а.
|
№ систиеми /а |
|
|
|
|
|
1 |
(1;+∞) |
|
І |
- |
- |
- |
1 |
2 |
2 |
1 |
|
ІІ |
1 |
1 |
1 |
1 |
1 |
- |
- |
Відповідь . 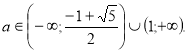
Приклад 2.
При будь - якому а розв’язати рівняння ![]()
Розв’язання.
х=-1, х=-а – нулі модулів. –а -1
І. Нехай – а<-1, тобто а>1. ---------І------------І-------→
1) х<-а
-2х-2-х-а=4,
-3х=6+а,
х = - 6+а
3
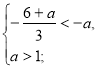
![]()
![]() а є (1;3).
а є (1;3).
2)-а≤х<-1
-2х-2+х+а=4
х=а-6
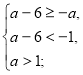
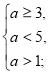 а є [3;5).
а є [3;5).
3) х≥-1
2х+2+х+а=4; 3х=2-а; ![]()
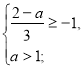
![]()
![]()
![]()
ІІ. –а=-1, а=1
2|х+1|+|х+1|=4
3·|х+1|=4; |х+1|=![]()
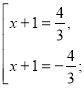
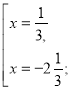
ІІІ. -а>-1, тобто а<1 --------|------------|--------→
-1 -а
1) х<-1
-2х-2-х-а=4; х= - ![]()
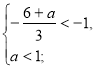
![]()
![]() а є (-3;1).
а є (-3;1).
2) -1≤х<-а
2х+2-х-а=4, х=2+а
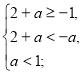
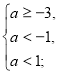 а є [-3;-1).
а є [-3;-1).
3) х≥-а
2х+2+х+а=4; 3х=2-а; х= ![]()
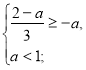
![]()
![]() а є [-1;1).
а є [-1;1).
Відповідь. Якщо а є ![]() то х
то х ![]() ;
;
якщо а є [-3;-1), то ![]() =2+а,
=2+а, ![]() =
=![]()
якщо а є [-1;3), то ![]() =
=![]() ;
; ![]() =
=![]()
якщо а є [3;5], то ![]() =
=![]()
![]() =а-6.
=а-6.
Приклад 3. Знайти всі значення параметра а, при кожному з яких рівняння ![]() має два різні корені.
має два різні корені.
Розв’язування.
І Нехай а є (-∞;-1).
1 2 3
--------------|-----------------|-------------→
![]() а
а
1) х є (-∞;![]() )
)
![]() -х-х+а=а(а-1)
-х-х+а=а(а-1)
-2х=-![]() -а+
-а+![]() -а
-а
-2х=-![]() +
+![]() -2а
-2а
х=![]()
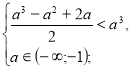
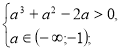
![]()
![]()
а є (-2;-1).
2) х є [![]() ;а)
;а)
-![]() +х-х+а=а(а-1)
+х-х+а=а(а-1)
ох=![]() -а+
-а+![]() -а
-а
ох=![]() +
+![]() -2а
-2а
якщо а≠-2, то х є ø, тому , якщо а є (-∞;-2)U(-2;-1), то х є ø, якщо а=-2, то х є R (тобто задовольняється умова задачі).
3) х є [а;+∞)
-![]() +х+х-а=а(а-1)
+х+х-а=а(а-1)
2х=![]() +а+
+а+![]() -а
-а
2х=![]() +
+![]() ; х=
; х=![]()
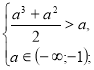
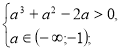
![]()
![]()
а є (-2;-1).
Робимо висновок про те, що при а є [-2;-1) дане рівняння два різні корені (![]() =
=![]()
![]() =
=![]()
![]() ≠
≠![]() ).
).
ІІ. а=-1.
![]()
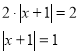
х+1=1 або х+1=-1
х=0 або х=-2.
Висновок при а=-1 дане рівняння має два різні корені.
ІІІ. а є (-1;0)
1 а 2 ![]() 3
3
--------|--------------|-------------→
1) х є (-∞;а)
![]() -х-х+а=а(а-1)
-х-х+а=а(а-1)
-2х=-![]() -а+
-а+![]() -а
-а
-2х=-![]() +
+![]() -2а
-2а
х=![]()
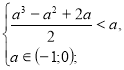
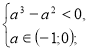
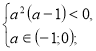
![]() а є (-1;0).
а є (-1;0).
2) х є [а; ![]() )
)
![]() -х+х-а=а(а-1)
-х+х-а=а(а-1)
ох=-![]() +а+
+а+![]() -а
-а
ох=-![]() +
+![]()
при а≠0 отримане рівняння не має розв’язків (х є ø).
3) х є [![]() ;+∞)
;+∞)
-![]() +х+х-а=а(а-1)
+х+х-а=а(а-1)
2х=![]() +а+
+а+![]() -а
-а
2х=![]() +
+![]()
х=![]() ;
; 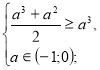
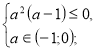
![]() а є (-1;0).
а є (-1;0).
Висновок: при а є (-1;0) дане рівняння має два різні корені ( ![]() =
=![]()
![]() =
=![]() ).
).
ІУ. а=0.
![]()
х=0
Отже, при а=0 умова задачі не задовольняється.
У. а є (0;1)
1 2 3
--------------|-----------------|-------------→
![]() а
а
1) х є (-∞;![]() ).
).
![]() -х-х+а=-а(а-1)
-х-х+а=-а(а-1)
-2х=-![]() -а-
-а-![]() +а
+а
-2х=-![]() -
-![]()
х=![]()
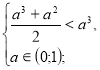
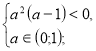
![]() а є (0;1).
а є (0;1).
2) х є [![]() ;а)
;а)
-![]() +х-х+а=-а(а-1)
+х-х+а=-а(а-1)
ох=![]() -а+
-а+![]() +а
+а
ох=![]() +
+![]() при а є (0;1), х є ø.
при а є (0;1), х є ø.
3) х є [а;+∞).
-![]() +х+х-а=-а(а-1)
+х+х-а=-а(а-1)
2х=![]() +а-
+а-![]() +а
+а
2х=![]() -
-![]() +2а
+2а
х=![]()
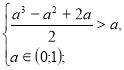
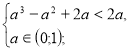
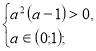
![]() а
а![]() .
.
Отже, при а є (0;1) дане рівняння має один розв’язок х=![]() , тому при цих значеннях параметра а умова задачі не задовольняється.
, тому при цих значеннях параметра а умова задачі не задовольняється.
УІ. а=1.
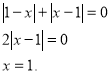
Отже, при а=1 рівняння має тільки один розв’язок.
УІІ. а є (1;+∞)
1 2 3
--------------|-----------------|-------------→
а ![]()
1) х є (-∞;а).
![]() -х-х+а=а(а-1)
-х-х+а=а(а-1)
-2х=-![]() -а+
-а+![]() -а
-а
х=![]()
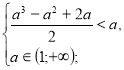
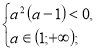
![]() а
а![]() .
.
2) х є [а; ![]() ).
).
![]() -х+х-а=а(а-1)
-х+х-а=а(а-1)
ох=-![]() +а+
+а+![]() -а
-а
ох=-![]() +
+![]() при а є (1;+∞), то х
при а є (1;+∞), то х![]() .
.
3) х є [![]() ;+∞)
;+∞)
-![]() +х+х-а=а(а-1)
+х+х-а=а(а-1)
2х=![]() +а+
+а+![]() -а
-а
2х=![]() +
+![]()
х=![]()
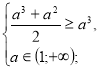
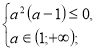
![]() а
а![]() .
.
Висновок: при а є (1;+∞) дане рівняння не має розв’язків, а тому не задовольняється умова задачі.
Відповідь. а є [-2;-1].
Часто при розв’язуванні рівнянь з параметрами, що містять змінну під знаком модуля, зручно використовувати графічний метод.
Приклад 4. Знайти всі значення параметра а, при кожному з яких рівняння ![]() має не менше двох розв’язків.
має не менше двох розв’язків.
Розв’язування.
Розглянемо функції у=![]() і у=а.
і у=а.
Побудуємо в одній системі координат графіки обох функцій.
у=![]()
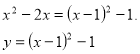 графіком є парабола, вітки якої напрямлені вгору, а вершина має координати (1;-1).
графіком є парабола, вітки якої напрямлені вгору, а вершина має координати (1;-1).
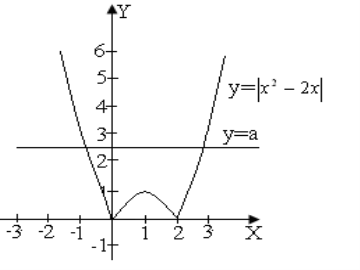
Відповідь. а є [0;+∞).
Приклад 5.
Для всіх значень а встановити кількість розв’язків рівняння.
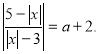
Розв’язування.
Розглянемо функції у=![]() то у=а+2.
то у=а+2.
![]() у=
у=![]()
Вкажемо послідовність побудови графіка даної функції.
1) у=![]() 2) у=
2) у=![]() 3) у=
3) у=![]() 4) у=
4) у=
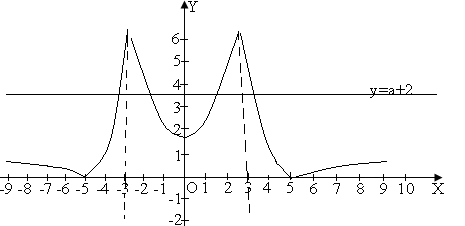
Відповідь. Якщо а є ![]() то рівняння не має розв’язків; якщо а=-2, то два розв’язки; якщо а є (-2;-1), то чотири розв’язки; якщо а є [-1;-
то рівняння не має розв’язків; якщо а=-2, то два розв’язки; якщо а є (-2;-1), то чотири розв’язки; якщо а є [-1;- ![]() ), то два розв’язки; якщо а=-
), то два розв’язки; якщо а=-![]() , то три розв’язки; якщо а є (-
, то три розв’язки; якщо а є (-![]() ;+∞), то чотири розв’язки.
;+∞), то чотири розв’язки.
Приклади 6.
Знайти всі значення параметра а, при кожному з яких рівняння має два різні корені.
![]()
Розв’язування.
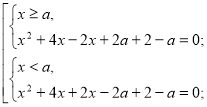
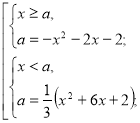 х=а
х=а
Побудуємо графіки функцій а=-![]() та а=
та а=![]() (
(![]() ) в системі координат х о а, розглядаючи їх у відповідних півплощинах (х≥а та х<а ).
) в системі координат х о а, розглядаючи їх у відповідних півплощинах (х≥а та х<а ).
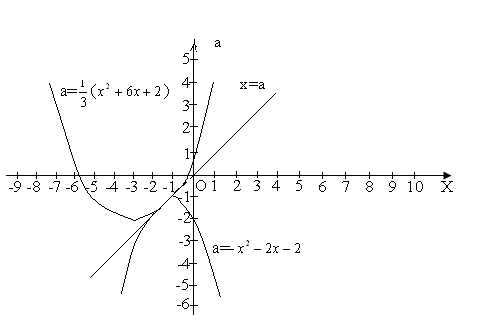
Для того,
щоб система мала два розв’язки, потрібно, щоб горизонтальна пряма перетинала графік двічі. Відповідь:ає(-∞;-![]() )U(-2;+∞)
)U(-2;+∞)
Оскільки при розв’язуванні ірраціональних рівнянь з параметрами виконати перевірку всіх коренів виможливо, то розв’язуємо ці рівняння з урахуванням області допустимих значень змінних, пам’ятаючи, що якщо обидві частини рівняння ƒ(х)=g(х) невід’ємні, та рівняння ƒ(х)=g(х) і (ƒ(х))![]() (g(х))
(g(х))![]() рівносильні.
рівносильні.
Приклад 1.
При будь-якому значенні а розв’язати рівняння ![]()
Розв’язування.
ОДЗ
![]()
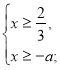
Підносимо до квадрату обидві частини рівності.
![]()
3х-2=![]() +2ах+
+2ах+![]()
![]() +(2а-3)х+
+(2а-3)х+![]() +2=0.
+2=0.
1)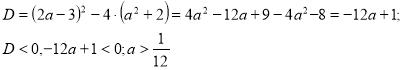
х є ø.
2)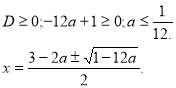
Перевіримо, при яких значеннях а ![]() задовольняє ОДЗ.
задовольняє ОДЗ.
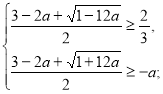
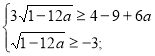 (1)
(1)
Розв’яжемо окремо кожну з ірраціональних нерівностей системи.
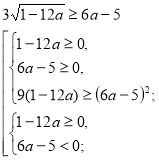

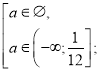 а є (-∞;
а є (-∞;![]() .
.
![]() ; а є (-∞;
; а є (-∞;![]() .
.
Тому розв’язок системи (1) а є (-∞;![]() .
.
Отже х=![]() є розв’язком даного рівняння при а є
є розв’язком даного рівняння при а є ![]()
Перевіримо, при яких значеннях а ![]() задовольняє ОДЗ.
задовольняє ОДЗ.
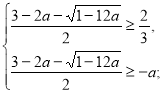 (2)
(2) 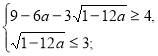
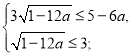
Розв’яжемо кожну з ірраціональних нерівностей системи окремо.
![]()
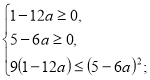
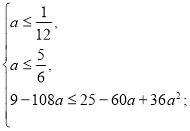
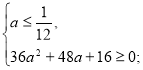
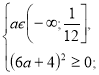
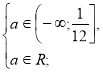 а є (-∞;
а є (-∞;![]() .
.
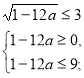
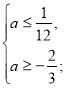
![]()
Повертаємося до системи (2).
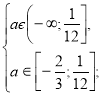
![]()
Отже, ![]() є розв’язком даного рівняння при
є розв’язком даного рівняння при ![]()
Відповідь. Якщо а є (-∞;-![]() , то
, то ![]() якщо
якщо ![]() , то
, то ![]()
![]() ; якщо
; якщо ![]() то х
то х ![]() .
.
Приклад 2. При будь якому значенні а розв’язати рівняння ![]()
Розв’язування.
ОДЗ.![]()
Підносимо до квадрату обидві частини рівності.
![]()
2ах-1=![]() -2х+1
-2х+1
![]() -(2а+2)х+2=0
-(2а+2)х+2=0
![]()
1) ![]()
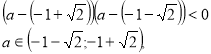
отже, якщо ![]() то х є ø.
то х є ø.
2) ![]()
![]()
Знайдемо значення а, при яких ![]() належить ОДЗ.
належить ОДЗ.
![]()
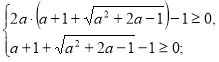 (1)
(1)
Розв’яжемо окремо кожну з ірраціональних нерівностей системи.
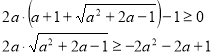
Якщо а>0, то ![]()
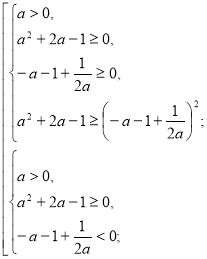
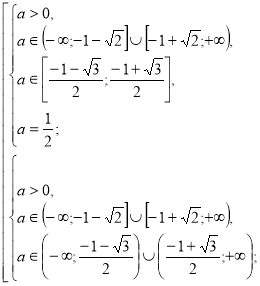
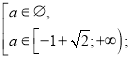
![]()
Якщо а<0
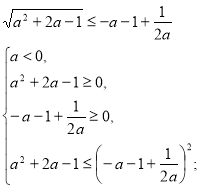
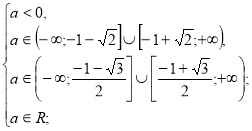
![]()
Об’єднуємо отримані розв’язки.
![]()
![]()
![]()
![]()
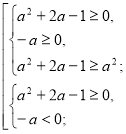
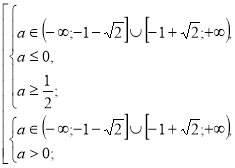
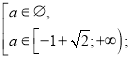
![]()
Повертаємося до системи (1).
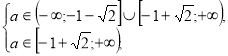
![]() при таких значеннях параметра
при таких значеннях параметра ![]() є розв’язком даного рівняння.
є розв’язком даного рівняння.
Знайдемо значення а, при яких ![]() належить ОДЗ.
належить ОДЗ.
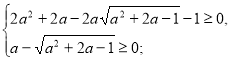 (2)
(2)
Розв’яжемо окремо кожну з нерівностей системи.
![]()
якщо а>0, то ![]()
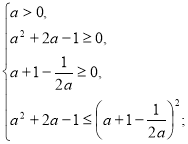
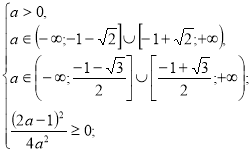
![]()
Якщо а<0, то ![]()
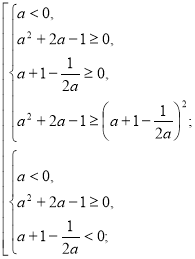
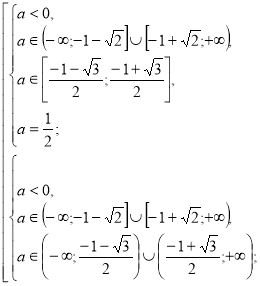
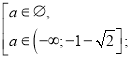
![]() .
.
![]()
![]()
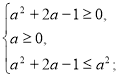
![]()
Повертаємося до системи (2).
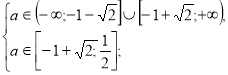
![]() - при таких значеннях параметра а
- при таких значеннях параметра а ![]() є розв’язком даного рівняння.
є розв’язком даного рівняння.
Відповідь. Якщо ![]() , то х
, то х ![]() ;
;
Якщо ![]() , то
, то ![]() ,
, ![]() ;
;
Якщо ![]() то
то ![]()
Приклад 3. При будь-якому значенні параметра а розв’язати рівняння. ![]()
Розв’язання.
ОДЗ. ![]()
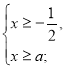
2х+1=![]() -2ах+
-2ах+![]()
![]() -(2а-2)х+
-(2а-2)х+![]() -1=0.
-1=0.
![]()
1)![]() 2а+2<0, а<-1, х є ø.
2а+2<0, а<-1, х є ø.
2) ![]() 2а+2≥0, а≥-1.
2а+2≥0, а≥-1.
![]()
Знайдемо, при яких значеннях параметра а ![]() належать ОДЗ рівняння.
належать ОДЗ рівняння.
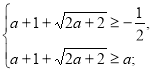 (1)
(1)
Розв’яжемо окремо кожну з нерівностей системи.
![]()
![]()
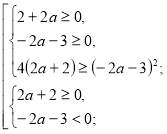
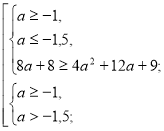
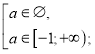
![]()
![]()
![]()
![]()
Повертаємося до системи (1).
![]()
![]()
Отже, ![]() є розв’язком даного рівняння, якщо
є розв’язком даного рівняння, якщо ![]()
Знайдемо при яких значеннях параметра а ![]() належить ОДЗ рівняння.
належить ОДЗ рівняння.
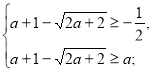 (2)
(2)
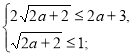
Розв’яжемо окремо кожну з нерівностей системи (2).
![]()
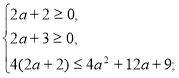
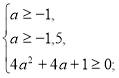
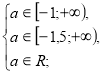
![]()
![]()
![]()
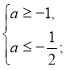
![]()
Повертаємося до системи (2).
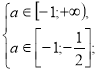
![]()
Отже, при ![]()
![]() є розв’язком даного рівняння.
є розв’язком даного рівняння.
Відповідь. Якщо ![]() , то х
, то х ![]() ;
;
Якщо ![]() , то
, то ![]() ,
, ![]() ;
;
Якщо ![]() то
то ![]()
Приклад 4. При будь-якому значенні параметра а розв’язати рівняння. ![]()
Розв’язання.
ОДЗ. 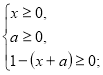
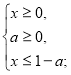
Підносимо до квадрату обидві частини рівності. ![]()
![]()
![]()
Для того, щоб не з’явилися сторонні корені, звужуємо ОДЗ.
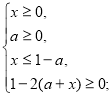
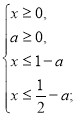
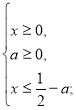
![]()
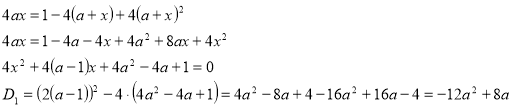
1) ![]()
Якщо ![]() , то х є ø.
, то х є ø.
2) ![]()
![]()
![]()
![]()
Знайдемо при яких значеннях параметра а ![]() належить ОДЗ.
належить ОДЗ.
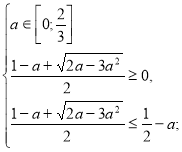
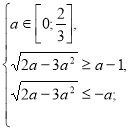 (1)
(1)
Розв’яжемо окремо кожну з ірраціональних нерівностей системи.
![]()
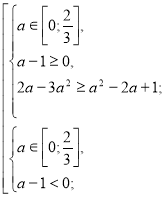
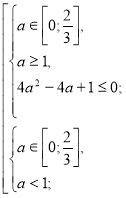
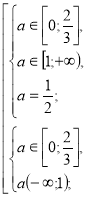
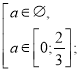
![]()
![]()
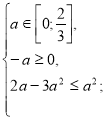
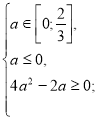
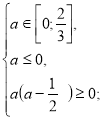
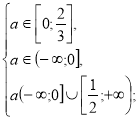 а=0.
а=0.
Повертаємося до системи (1).
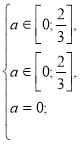
а=0.
Отже, якщо а=0, то ![]() є коренем даного рівняння.
є коренем даного рівняння.
Знайдемо значення параметра а, при яких ![]() є коренем даного рівняння.
є коренем даного рівняння.
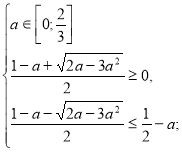
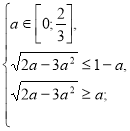 (2)
(2)
Розв’яжемо окремо кожну з ірраціональних нерівностей системи (2).
![]()
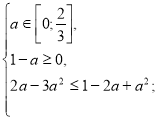
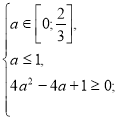
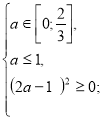
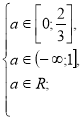
![]()
![]()
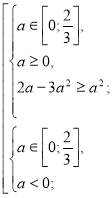
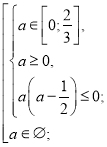
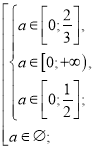
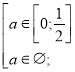
![]()
Повертаємося до системи (2).
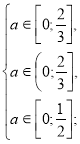
![]()
Отже ![]() є розв’язком даного рівняння, якщо
є розв’язком даного рівняння, якщо ![]()
Відповідь. Якщо ![]()
![]() то х
то х![]() ;
;
Якщо ![]() , то
, то ![]() ,
,![]()
Якщо ![]() то
то ![]()
Приклад 5. При будь-якому значенні параметра а розв’язати рівняння. ![]()
Розв’язання.
ОДЗ. 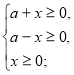
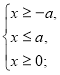
![]()
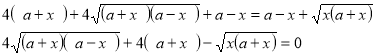
![]()
![]() або
або ![]()
![]()
![]() або
або ![]()
![]()
![]() або
або ![]()
![]()
Звуження ОДЗ. ![]()
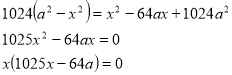
х=0 або ![]()
Знайдемо значення параметра а, при яких х=-а є розв’язком даного рівняння.
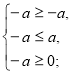
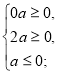
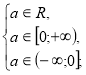 а=0.
а=0.
Отже, х=-а, якщо а=0.
Знайдемо значення параметра а, при яких х=0 є розв’язком даного рівняння.
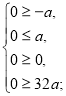
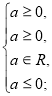 а=0.
а=0.
Отже, х=0 є розв’язком даного рівняння, якщо а=0.
Знайдемо значення параметра а, при яких ![]() є розв’язком даного рівняння.
є розв’язком даного рівняння.
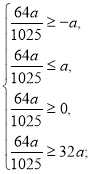
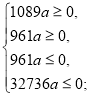
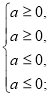 а=0.
а=0.
Отже, ![]() є розв’язком даного рівняння а=0.
є розв’язком даного рівняння а=0.
Відповідь. Якщо а=0, то х=-а, х=0; ![]() ;
;
якщо а≠0, то х ![]() .
.
Приклад 6. При будь-якому значенні параметра а розв’язати рівняння
![]()
Розв’язування.
ОДЗ.
![]()
![]()
![]()
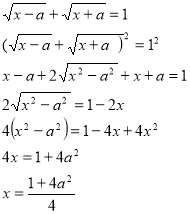
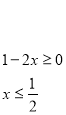
Знайдемо значення параметра а, при яких ![]() належить ОДЗ.
належить ОДЗ.
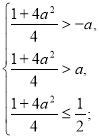
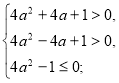
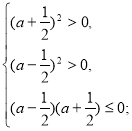
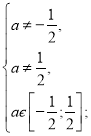
![]()
Відповідь. Якщо ![]() , то
, то ![]() ;
;
Якщо ![]() то х
то х ![]() .
.
Приклад 7. При будь-якому значенні параметра а розв’язати рівняння ![]()
Розв’язання
![]()
нехай ![]() =t, t≥0
=t, t≥0
![]()
![]()
ОДЗ. 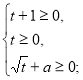
t+1=t+2a![]()
![]()
1) a=0; ![]() t є ø.
t є ø.
2) 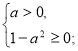
![]()
![]()
![]()
t=![]()
Перевіримо, при яких значення а t=![]() належить ОДЗ.
належить ОДЗ.
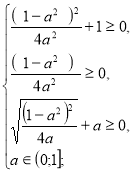
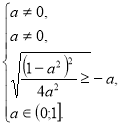 а є
а є ![]()
Повертаємося до заміни.
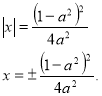
Відповідь. . Якщо ![]() то
то ![]()
![]()
Якщо ![]() то х
то х ![]() .
.


про публікацію авторської розробки
Додати розробку