Збірник різнорівненвих завдань з теми "Квадратні рівняння"

Про матеріал

Представлені дидактичні матеріали призначені для організації самостійної роботи учнів та для здійснення контролю знань, умінь і навичок, для забезпечення диференційованого підходу при підготовці домашнього завдання.

Самостійні роботи поділено на чотири групи з урахуванням характеру навчальної діяльності, яка визначається системою завдань та відповідає відповідному методу навчання: репродуктивному, частково пошуковому, дослідницькому:

1) самостійні роботи за зразком, тобто найпростіші відтворювальні самостійні роботи;

2) реконструктивно-варіативні самостійні роботи;

3) частково пошукові самостійні роботи;

4) творчі, дослідницькі самостійні роботи.

Дані дидактичні матеріали також можуть бути використані як ефективний засіб закріплення, поглиблення, повторення і розширення теоретичних та практичних знань і умінь, для розвитку творчої математичної діяльності учнів.

Перегляд файлу

Бердичівська загальноосвітня школа-інтернат І-ІІІ ст..

для дітей-сиріт і дітей, позбавлених батьківського піклування

Формування компетентності «вчись вчитися» - одне з головних завдань сучасної школи. Навчання математиці передбачає реалізацію діяльнісного підходу як головної умови забезпечення ефективності математичної освіти, оволодіння загальною математичною культурою, вироблення математичного стилю мислення. Основною метою своєї роботи вважаю формування в учнів стійкої мотивації до навчально-пізнавальної діяльності. Тому, при підготовці до вивчення кожного з розділів добираю систему завдань та стимулюю учнів до самостійної та систематичної роботи з відпрацювання обчислювальних навичок, розвитку формально-оперативних умінь.

Рівняння в шкільному курсі алгебри займають провідне місце. На їх вивчення відводиться часу більше, ніж на будь-яку іншу тему шкільного курсу математики. Сила теорії рівнянь в тому, що вона не тільки має теоретичне значення для пізнання природних законів, але і служить конкретним практичним цілям. Більшість задач про просторові форми і кількісні співвідношення реального світу зводиться до складання та розв’язування різних видів рівнянь. Опановуючи способами їх вирішення, діти знаходять відповіді на різні питання з науки і техніки (транспорт, сільське господарство, промисловість, зв'язок і т.і.). Неабиякого значення для формування вміння розв'язувати рівняння має самостійна робота учнів.

Серед методів, які спрямовані на активізацію пізнавальної діяльності учнів, важлива роль належить самостійній роботі. Термін «самостійна робота» вживають у різних значеннях. Часто так називають окремі уроки, присвячені самостійному розв'язуванню задач, які дуже схожі на контрольні роботи. Але це тільки один з видів самостійної роботи, причому не основний.

При укладанні даного збірника у термін «самостійна робота» я намагалася вкласти значно ширший зміст, віднесла сюди і самостійне вивчення теорії за підручником, і самостійне опановування учнями способів розв’язування квадратних рівнянь, і самостійне розв'язування задач за допомогою квадратних рівнянь тощо. Самостійну роботу учнів, з огляду на те, що навчатись можна не тільки з слів учителя, не тільки під час колективного розв'язування задач і вправ, а й самостійно, розглядаю як метод навчання, як освітню технологію.

Працюючи самостійно, учні, як правило, глибше вдумуються в зміст опрацьованого матеріалу, краще зосереджують свою увагу, ніж це звичайно буває при поясненнях учителя або розповідях учнів. Тому знання, уміння і навички, набуті учнями в результаті добре організованої самостійної роботи, бувають міцнішими і ґрунтовнішими. Крім того, у процесі самостійної роботи в учнів виховується наполегливість, увага, витримка та інші корисні якості.

Представлені вашій увазі дидактичні матеріали призначені для організації самостійної роботи учнів та для здійснення контролю знань, умінь і навичок, для забезпечення диференційованого підходу при підготовці домашнього завдання.

1) самостійні роботи за зразком, тобто найпростіші відтворювальні самостійні роботи;

2) реконструктивно-варіативні самостійні роботи;

3) частково пошукові самостійні роботи;

4) творчі, дослідницькі самостійні роботи.

Методичні рекомендації

Найважливішою умовою і засобом плідної навчальної діяльності учнів, спрямованої на успішний розвиток у них досвіду творчої діяльності, є організація самостійної роботи школярів в процесі навчання. Особливо важлива така самостійна робота, в ході якої учень повинен постійно переносити як відомі, так і знову сконструйовані способи вирішення в нові ситуації пізнавальної діяльності.

Самостійна робота учнів це такий спосіб навчальної роботи, де:

1) учням пропонуються навчальні завдання та інструктаж для їх виконання,

2) робота проводиться без безпосередньої участі вчителя, але під його керівництвом,

3) виконання роботи вимагає від учнів розумової напруги.

Самостійна робота активізує учнів в тому сенсі, що всі учні, навіть більш пасивні і ліниві, повинні виконувати завдання самі.

Навчальні завдання для самостійної роботи різноманітні, вони залежать від навчальних умінь учнів. Сильні учні володіють раціональними і більш складними навчальними уміннями. Слабкі ж учні обмежуються в основному вміннями, пов'язаними з репродуктивною діяльністю.

Навчальні завдання діляться на 4 логічних основи:

1) за методом самостійної роботи учнів (спостереження, вправи, робота з підручником);

2) по ланках навчального процесу (завдання на сприйняття, систематизацію, закріплення і повторення навчального матеріалу);

3) за характером пізнавальної діяльності учнів (репродуктивні і творчі завдання);

4) за характером керівництва (докладний, менш докладний інструктаж).

За характером навчальної самостійної діяльності учнів можна виділити чотири види робіт виходячи з поступового підвищення рівня самостійності.

Перший рівень - найпростіша самостійність (за зразком)

Учень виконує вправу, яка потребує простого відтворення наявних знань за правилом, за зразком, самостійно вирішує завдання, вправи за наданим прикладом.

Виконуючи самостійні роботи цього виду, учням необхідно зробити пряме перенесення відомого способу діяльності в аналогічній ситуації.

Другий рівень - реконструктивно - варіативна самостійність

Учневі слід вміти з кількох наявних правил, визначень, зразків міркувань і т.і. вибрати одне визначення і використовувати його в процесі самостійного рішення нового завдання. На даному рівні учень показує вміння застосовувати розумові операції, такі як порівняння, аналіз. Аналізуючи умови завдання, учень перебирає наявні в його розпорядженні засоби для її вирішення, порівнює їх і вибирає більш дієвий спосіб з деякою модифікацією в незвичайні внутрішньопредметні та межпредметні проблемні ситуації. Наприклад, математичні завдання вирішуються за допомогою перенесення способу розв'язання геометричних задач.

Третій рівень - частково пошукова самостійність

Частково пошукова самостійність проявляється в умінні з наявного арсеналу правил та інструкцій для вирішення завдань певного розділу математики, формувати (комбінувати) узагальнені способи для вирішення більш широкого класу задач, у тому числі й з інших розділів математики. В умінні здійснювати перенесення математичних методів, розглянутих в одному розділі, на вирішення завдань з інших розділів або з суміжних навчальних предметів; в прагненні знайти «власне правило», прийом, спосіб діяльності; в пошуках кількох способів вирішення завдання й у виборі найбільш раціонального, витонченого; в варіюванні умов завдання і в порівнянні відповідних способів рішення і т.і.. Тут вже існують елементи творчості. Учень на цьому рівні володіє відносно великим набором прийомів розумової діяльності - вміє проводити порівняння, аналіз, синтез, абстрагування тощо. У його діяльності значне місце займає контроль результатів і самоконтроль. Він може самостійно спланувати та організувати свою навчальну діяльність.

Вищий, четвертий рівень самостійності - творча, дослідницька

Самостійні роботи всіх цих видів включають в себе певні проблемні ситуації, що стимулюють і орієнтують учня на пошук теоретичних знань і способів діяльності різного ступеня складності (за принципом наростання).

Самостійність рішення полягає у тому, що учень по заданій умові розчленовує загальну задачу на кілька завдань, визначає шляхи їх вирішення, а потім результати кожної з них об'єднує, зіставляє, комбінує і отримує загальний результат.

Такі види самостійних робіт, які лежать в основі навчання школярів теоретичних знань як інструменту пізнання, формують у дітей вміння планувати власну пізнавальну діяльність, контролювати її хід.

Кожен з перелічених видів робіт включає в себе певні проблемні ситуації, що спонукають до творчої, дослідницької роботи у напрямку відшуковування способів розв’язування. Залежно від знайденого способу розв'язання, учень спрямовує свої пошуки на розвиток і обгрунтування цього способу. Колишні знання і досвід самостійної пізнавальної і практичної діяльності використовуються при цьому залежно від умов завдання.

Найвища ступінь самостійності - вміння вирішувати дослідницькі завдання. Сюди входить уміння самостійно формулювати завдання різного ступеня складності в заданій ситуації, ставити проблеми і розробляти план їх вирішення, визначати пошук рішення і будувати його гіпотезу.

Неповні квадратні рівняння

I. Найпростіша відтворювальна самостійна робота

(за зразком)

Таблиця № 1

Розв’язування неповних квадратних рівнянь

Коефіці-єнт	b = 0		c = 0	b = 0 і c = 0
Вигляд	ax² *+ c = 0*		ax² *+ bx = 0*	ax² *= 0*
Загальний розв’язок	ax² = -c x² =		x (ax + b) = 0 x₁ = 0 або ax + b = 0 ax = -b x₂ =- два розв’язки Відповідь: x₁ = 0, x₂ = -b/a	x² = 0 x = 0
	Якщо > 0	Якщо < 0
	x₁ = x₂ = -	Рівняння розв’язків не має
Приклад	2x² -18 = 0 2x² = 18 x² = 9 9 > 0 x₁ = √9 = 3 x₁ = -√9 = -3 Відповідь: -3: 3		2x² – 7x = 0 x (2x - 7) = 0 x = 0 або 2x – 7 = 0 2x = 7 x = 3,5 Відповідь: 0; 3,5	7x² = 0 x² = 0 x = 0 Відповідь: 0
Розв’яжи сам	2x² – 8 = 0		2x² + 3x = 0	9x² = 0

Розв’яжіть рівняння за зразком:

х² - 6х = 0; 0,5х² - 7,5 = 0; х² = 2;

Зх²- 11=0; х²= 81; 3 - х² = 0;

8х - х² = 0; х² - 25 = 0; 5х²- 15х = 0;

-х²- 11=0; 6084 -х²= 0; 49х - х² = 0;

х² = 0,09; 2х² - 98 = 0; 2х² + х = 0;

х² + 4х = 0; х² = -3; 49х² = 0;

х²= -961; 2х² + 8 = 0; Зх²+ 75 = 0;

4 - 2х²= 6; 7х² =21952; 0,1х² - 547,6 = 0.

Запишіть квадратне рівняння, коефіцієнти якого дорівнюють:

Коефіцієнти рівняння			Квадратне рівняння
а	в	с	ах²*+вх.+с=0*
7	-2	5
-11	4	0
1	8	-3
-1,8	0	-2,3

II. Реконструктивно-варіативна самостійна робота

1. Доведіть, що:

а) Кожне з чисел 7 та -7 є коренем рівняння 2х² - 98 = 0;

б) Кожне з чисел 0 та -4 є коренем рівняння х² - 98 = 0.

Розв’язуючи рівняння 0,5х² - 7,5 = 0, учень знайшов, що корені дорівнюють 3 та -3.
Доведіть, що він помилився.

При яких значеннях b рівні значення двочленів b² + 6b та Зb² - b?

Складіть квадратне рівняння, у якому:

1) старший коефіцієнт дорівнює 6, другий коефіцієнт дорівнює 7, а вільний член дорівнює 2;

2) старший коефіцієнт дорівнює 1, другий коефіцієнт дорівнює –8, а вільний член дорівнює −

3) старший коефіцієнт дорівнює 7,2, другий коефіцієнт дорівнює –2, а вільний член дорівнює 0.

5. Розв’яжіть рівняння:

а) (3х-1)(2х-2) = (х-4)²+ 6;

б) 6х - 6(х - 4) = (2х - 1) (2х + 1);

в) (3х - 4)² - (5х + 2) (2х + 8) = 0;

г) (2х - 1) (2х + 3) - (х + 2)² = 0.

6.Розв’яжіть рівняння:

а) ; б)

в) г)

III. Частково пошукова самостійна робота

Розв’яжіть рівняння:

а) б) ;

в)

2. Складіть квадратне рівняння, яке має такі корені:

а) 5 і 7; б) 4 і – 4; в) 0 і 11.

3. Подайте дане рівняння у вигляді ax² + bx + c = 0, укажіть значення коефіцієнтів a, b і c:

1) 6x (3 – x) = 7 – 2x²; 2) (5x – 1)² = (x + 4) (x – 2).

4. Розв’яжіть рівняння:

а) (5х-1)²-( 3х + 2)² + (х-1)(х+1) = х - 4;

б) 12 х² - (3х + 2)² + (х + 4) (5х - 1) = х² - 8;

в)

г)

IV. Творча, дослідницька самостійна робота

Сума квадратів двох послідовних цілих чисел на 17 більша за подвоєне більше з них. Знайдіть ці числа.

При якому значенні m не є квадратним рівняння:

а) (m – 4) x² + mx + 7 = 0;

б) (m² + 8m) x² + (m + 8) x + 10 = 0;

в) (m² – 81) x² – 6x + m = 0.

Складіть квадратне рівняння з числовими коефіцієнтами, корені якого пов’язані співвідношенням 2х₁=3х₂.

Розв’яжіть відносно х рівняння, в якому а ≠ 0:

а) ах² = 9;

б) ах² - = 0;

в) 6,25 – а²х² = 0;

г) ах² – = 0.

Розв’язування квадратних рівнянь

виділенням квадрата двочлена

I. Найпростіша відтворювальна самостійна робота

1.Розв’яжіть рівняння, виділивши повний квадрат суми або різниці (за формулою а² ± 2аb + b² = (a ± b)²).

а) х² + 2х + 1 = 0; г) х² + 6х + 9 = 0; б) х²- 2х + 1 = 0; д) х² - 14х + 49= 0;

в) х²- 6х + 9 = 0; е) х² + 8х + 16 = 0.

II. Реконструктивно-варіативна самостійна робота

1.Розв’яжіть рівняння, виділивши повний квадрат суми або різниці

а) х² + 2х + 1 = 40; е) х² - 3х + 3 = 0;

б) х² - 8х + 15 = 0; є) х² + 8х + 15 = 0;

в) х² +12х + 20 = 0; ж) х² + 9х + 14 = 0;

г) х² - 5х - 61 = 0; з) х² - 2х - 1 = 0;

д) х² - 8х - 9 = 0; и) х² + 4х + 3 = 0.

III. Частково пошукова самостійна робота

1.Розв’яжіть рівняння, виділенням квадрата двочлена

а) 9 х² - 30х + 25 = 0;

б) -2х² - 6х + 1,5 = 0;

в) (х – 0,2-3)(х+)(х+2,1)=0

г) 2х² - 9х + 10 = 0;

д) 5х² + 3х - 8 = 0;

е) 5х² + 14х - 3 = 0.

IV. Творча, дослідницька самостійна робота

Добуток двох чисел дорівнює їх середньому арифметичному, а різниця цих чисел рівна 1. Знайдіть ці числа.

Різниця двох чисел дорівнює 2, а половина добутку цих чисел рівна їх середньому арифметичному. Знайдіть ці числа.

Розв’язування рівнянь

за допомогою формули коренів квадратного рівняння

Повне квадратне рівняння

ах²+вх.+с=0,

а≠0, в≠0, с≠0

Дискримінант квадратного рівняння

D=b² – 4ac

D>0

D=0

D<0

х₁= ;
х₂=.

х=

Рівняння розв’язків немає

I. Найпростіша відтворювальна самостійна робота

(за зразком)

Таблиця № 2

Розв’язування квадратних рівнянь за формулою коренів

Алгоритм

Приклад

Розв’яжи сам

ах² + bx + c = 0

Визначимо коефіцієнти

a = …, b = …, c = …

Обчислимо дискримінант за формулою

D = b² – 4ac = …

Порівняємо D з нулем.
а) якщо D > 0, то обраховуємо =

та знаходимо його корені:

х₁	=	- b +	=	…
		2a

х₂	=	- b -	=	…
		2a

Відповідь: х₁; х₂.

б) якщо D = 0, то знаходимо

х	=	- b
		2b

Відповідь: х.

в) якщо D < 0, то записуємо

Відповідь: розв’язків не має

х² - 4х + 3 = 0

a = 1, b = - 4, c = 3.

D = (-4)² 4 · 1 · 3 = 4

4 > 0

= 2

х₁

х₂

Відповідь: 1; 3.

х² + 5х + 4 = 0

1. Розв’яжіть рівняння за зразком:

а) 3х² - 13х + 4 = 0; є) –x² – 8x + 12 = 0;

б) 2x² – 5x + 2 = 0; ж) 5х² + 8х + 3 = 0;

в) 5х² - 13х + 6 = 0; з) х² - 10х - 24 = 0;

г) 9х² - 12х + 4 = 0; и) х² + 3х - 4 = 0;

д) 49х² - 28х + 3 = 0; і) х² - 3х + 28 = 0;

е) 18x² – 9x – 5 = 0; ї) х² + х + 8 = 0;

II. Реконструктивно-варіативна самостійна робота

1. Розв’яжіть рівняння, попередньо записавши їх в стандартному вигляді:

а) х² + 5х = 14;

б) 3х² = 2х – 5;

в) (4x – 3)² + (3x – 1) (3x + 1) = 9;

г) 25х² + 10 = 10х + 9;

д) (х - 2)(х + 2) + 14 = 9х – х²;

е) x² + 3x + 4 = 0;

є) 2х – 9 + 5х² = 2х² + 6х – 20;

ж) 2(2х² - 7) = - 8х – 9;

з) (x + 7) (x – 8) – (4x + 1) (x – 2) = –21x;

и) (3х + 1)² – х( 7х + 5) = 4;

і) ( х - 2)( х + 2 ) – 2х( х – 3 ) = 6 – х;

ї) (у + 1)² = - 1 – ( 3 + у )у;

й) х( х – 1 ) – 2х( х + 1) = х – (2х +1)(2х -1);

к) x² - x ( + 2) + 2 = 0.

III. Частково пошукова самостійна робота

Знайдіть корені рівняння:

|= х;

( 3 – х )² + 5 | 3 - х | - 6 = 0;

5( )² - 6 + 1 = 0;

2| у |² - 9| у | = 0;

4х⁴ + х² – 33 = 0;

– ( у + 5 )² + 3 | у + 5 | + 5 = 0;

2х² + 9( )² – 27= 0

1 – 18 | 2 – р | + 81( 2 – р )² = 0;

5x² – 8 | x | + 3 = 0;

| | x² – 6x + 4 | – 3 | = 1;

3 | х | ² – 14 | х | + 16 = 0;

5х – 16 + 3 = 0;

х⁶ + 2х³ - 3 = 0;

8 ( 1 – 2х ) ² – 14 | 2х – 1 | + 5 = 0;

12 ( 4х )²+ 64х – 3 = 0.

При яких значеннях х:

а) значення виразів ( х – 2 ) ² – 5 | х + 2 | - 3 та 2 | х + 2 | - 3 рівні;

б) вираз - 2х ⁴ + 5х ²+ 6 дорівнює виразу 4х ⁴ + 5х ²;

в) вираз ( ) ² – дорівнює виразу – 18;

г) вираз 3 () ² – 4 · + 3 дорівнює виразу () ² + + 1?

IV. Творча, дослідницька самостійна робота

Розв’яжіть рівняння:

а) | x² - 2x | = 3 - 2x;

б) | x – 2 | = x² – 2x;

в) | x² + x – 1 | = 2x – 1;

г) | 2x + 1 | = x² – x – 1.

2. При яких значеннях параметра b мають один корінь рівняння:

а) bx² – 6x – 7 = 0;

б) (b + 5) x² – (b + 6) x + 3 = 0;

в) (b – 4) x² + (2b – 8) x + 15 = 0;

г) (a + 2) x² + (a² + 2a) x + a + 2 = 0?

При яких значеннях параметра a рівняння

a (2a + 4) x² – (a + 2) x – 5a – 10 = 0 має більше ніж один розв’язок?

Теорема Вієта

I. Найпростіша відтворювальна самостійна робота

(за зразком)

Таблиця № 3

Формула

Приклади

x ² + p x + q = 0

x₁ + x₂ = - p

x₁x₂ = q

Знайдіть коефіцієнти b і c рівняння

x² + bx + c = 0, якщо його коренями є числа –7 і 4.

Розв’язання.

За теоремою Вієта b = –(–7 + 4) = 3,

c = –7· 4 = –28.

Відповідь: b = 3, c = –28.

2.Один з коренів квадратного рівняння дорівнює 2. Знайдіть другий корінь рівняння

x ² + 17 x - 38 = 0.

Розв’язання. 2 + х₂ = - 17 або 2 х₂= - 38

х ₂= - 17 – 2 х ₂= - 38 : 2

х₂= - 19 х ₂= - 19

Відповідь: - 19.

ах² + bx + c = 0

х² +	b	х +	c	= 0
	a		a

x₁ + x₂ = -

x₁·x₂ =

Знайдіть суму й добуток коренів рівняння

3x² – 15x + 2 = 0.

Розв’язання. З’ясуємо, чи має дане рівняння корені.

Маємо: D = (–15)² – 4·3·2 = 225 – 24 > 0. Отже, рівняння має два корені x₁ і x₂.

Тоді за теоремою Вієта x₁ + x₂ =

x₁x₂ = .

Складіть квадратне рівняння з цілими коефіцієнтами, корені якого дорівнюють: 4 і

Розв’язання. Нехай x₁ = 4 і x₂=

Тоді x₁ + x₂ = 4- , x₁x₂= 4· (-.

За теоремою, оберненою до теореми Вієта, числа x₁ і x₂ є коренями рівняння x² -

Помноживши обидві частини цього рівняння на 7, отримуємо квадратне рівняння з цілими коефіцієнтами:

7x² – 23x – 20 = 0.

Відповідь: 7x² – 23x – 20 = 0

Знайдіть суму і добуток коренів у таких рівняннях:

а) x ² - 12 x - 45 = 0; д) 60 z + z² = 0;

б) x ² - 16x + 28 = 0; е) 4,5у - у² = 0;

в) у ² + 17 у + 60 = 0; є) 3x ² - 6x - 7 = 0;

г) 5у ² + у - 3 = 0; ж) у ² - 12 = 0.

2.Встановіть відповідність (методом підбору)

	Рівняння		Корені рівняння
1	x ² - 4 x -5 = 0	А	3 і 7
2	x ² - 10 x+21 = 0	Б	-4 і -5
3	x ² +9 x+20 = 0	В	-3 і -2
4	x ² +3 x-18 = 0	Г	-1 і 5
5	x ² +5 x+6 = 0	Д	-6 і 3

3. Один з коренів квадратного рівняння рівний 2. Знайдіть другий корінь рівняння:

а) 7х² – 11х – 6 = 0; б) х² – 8х + 12 = 0.

4. Знайдіть коефіцієнти b і c рівняння x² + bx + c = 0, якщо його коренями є числа:

а) –2 і 0,5; б) –10 і –20.

5.Складіть квадратне рівняння з цілими коефіцієнтами, корені якого дорівнюють:

а) –7 і –8; б) 5 і –0,4;

в) г) 5 − і 5 + .

6.Складіть квадратне рівняння з цілими коефіцієнтами, корені якого дорівнюють:

а) 2 і 5; б) – 0,2 і –10; в) 0 і 6;

г) - і 2; д) 2 - і 2 + ; е) - і

II. Реконструктивно-варіативна самостійна робота

В рівнянні x ² + p x – 24 = 0 один з коренів дорівнює 12. Знайдіть другий корінь і коефіцієнт p.

Вказівка. Скористатися тим, що добуток коренів дорівнює – 24.

2. В рівнянні x² - 8x + q = 0 один з коренів дорівнює 12. Знайдіть другий корінь і коефіцієнт q.

х₁= 4, знайдіть х₂: 2х² - 9х + 4 = 0.

3. Один корінь дорівнює 1, знайдіть b : х² – bx =0

х₁= 5, знайдіть с: 2х² - 4х - с = 0.

х₁= - 2, знайдіть b: 3х² + bх - 2 = 0.

х₁= 4, знайдіть х₂: 2х² - bх + 8 = 0.

4.Застосовуючи теорему, обернену до теореми Вієта встановіть відповідність:

	Рівняння		Корені рівняння
1	x ² - 27 x = 0	А	-4 і 2
2	x² + 2x – 8 = 0	Б	і 1
3	x² – 3x – 18 = 0	В	0 і 27
4	x² + 5x + 4 = 0	Г	4- і -1
5	2x² – 5x + 3 = 0	Д	-3 і 6

III. Частково пошукова самостійна робота

Один з коренів рівняння 3х² - 9х + с = 0 на 2 більший другого. Знайдіть c.
При яких значеннях а рівняння х² – ( а + 4 )х – 3 = 0 має два корені, один з яких на 4 більший другого?
Відомо, що x₁ і x₂ — корені рівняння 2x² – 3x – 9 = 0. Не розв’язуючи рівняння, знайдіть значення виразу:

а) ; б) x₁² + x₂².

4. Корені рівняння x² + 20x + a = 0 відносяться як 7:3. Знайдіть значення a і корені рівняння.

IV. Творча, дослідницька самостійна робота

Дано квадратне рівняння ах² + bx + c = 0, де а ≠ 0

доведіть, що якщо a + b + c = 0 (тобто сума коефіцієнтів рівняння дорівнює нулю), то х₁ = 1, х₂= .

Не розв’язуючи рівняння х² – (m + 3n)x + 3mn = 0, обчисліть його суму коренів
Сума квадратів коренів рівняння 3x² + ax – 7 = 0 дорівнює . Знайдіть значення a.
При яких значеннях параметра a різниця коренів рівняння

2x² – (a + 1) x + a – 1 = 0 дорівнює їх добутку?

Розв’язування задач з допомогою квадратних рівнянь

I. Найпростіша відтворювальна самостійна робота

Городня ділянка, що має форму прямокутника, обнесена огорожею завдовжки 360 м. Визначте довжину і ширину ділянки, якщо відомо, що її площа дорівнює 8 000 м².

Заповніть пропуски та завершіть розв’язування задачі:

Нехай довжина ділянки дорівнює х м. Зваживши на те, що сума довжини та ширини ділянки обраховується за формулою периметра прямокутника, маємо, а+в=360:2=180 м. Тоді його ширина дорівнює (180 - х) м. Значить площа ділянки дорівнює _______________ м², що складає 8 000 м². Отримуємо рівняння __________________.

Різниця квадратів двох натуральних чисел, одне з яких утричі більше від іншого, дорівнює 200. Знайти ці числа. Яке з рівнянь відповідає умові задачі, якщо через х позначити менше число?

а) 3х·х=200; б) (3х)²+х²=200;

в) (3х)²- х²=200; г) 3х ² - х²=200.

Знайдіть число, яке на 12 менше його квадрата.

Відповідь: 4 та – 3.

Площа прямокутної пластини дорівнює 120 см ². Знайдіть довжину та ширину пластини, якщо відомо, що довжина на 2 см більша ширини.

Відповідь: 12 см та 10 см.

Добуток двох послідовних натуральних чисел на 271 більше їх суми. Знайдіть ці числа.

Відповідь: 17 і 18.

Спортивний майданчик має форму прямокутника, ширина якого на 4 м менша від довжини, а його площа дорівнює 96 м². Знайдіть розміри спортивного майданчика.
В прямокутному трикутнику гіпотенуза на 5см більша одного з катетів та на 10см більша другого. Знайдіть гіпотенузу.

Вказівка. Позначивши довжину гіпотенузи через х см, виразіть довжини катетів та скористайтеся теоремою Піфагора.

II. Реконструктивно-варіативна самостійна робота

Городня ділянка, що має форму прямокутника, одна сторона якого на 20 м більше іншої. Її потрібно обнести огорожею. Визначте довжину огорожі, якщо відомо, що площа ділянки дорівнює 8 000 м².
Від листа картону, що має форму квадрата, відрізали смугу шириною 3 см і площею 70 см². Знайдіть розміри аркуша картону.
Чисельник дробу на 5 більший від знаменника. Якщо до знаменника цього дробу додати 1, то одержимо дріб, сума якого і даного дробу дорівнюватиме 9. Знайдіть початковий дріб.
Знайди три послідовних натуральних числа, сума квадратів яких дорівнює 1589.
Діагональ прямокутника дорівнює 10 см, а одна зі сторін на 2 см більша від іншої. Знайти сторони прямокутника.

III. Частково пошукова самостійна робота

Периметр одного квадрата на 24 см менше периметра іншого, а його площа в 16 разів менше площі другого квадрата. Знайдіть сторони квадратів.
У прямокутному трикутнику один з катетів на 3 см менший від гіпотенузи, а інший на 6 см менший від гіпотенузи. Знайти гіпотенузу.
У прямокутнику одна сторона на 8 см менше діагоналі, а інша на 4 см менше діагоналі. Знайдіть площу прямокутника.
У прямокутному трикутнику гіпотенуза в 1 ¼ рази більша одного катета і на 8 см більша іншого. Знайдіть сторони трикутника.
Одне число на 4 більше іншого, а різниця їх кубів дорівнює 316. Знайдіть ці числа.

IV. Творча, дослідницька самостійна робота

Водний розчин солі містив 120 г води. Після того як до розчину додали 10 г солі, її концентрація збільшилася на 5 %. Скільки грамів солі містив розчин спочатку?
Сума кубів двох натуральних чисел дорівнює 1547. Знайдіть ці числа, якщо їх сума рівна 17.
За течією річки від пристані відійшов пліт. Через 4 год від цієї пристані в тому самому напрямку відійшов човен, який наздогнав пліт на відстані 15км від пристані. Знайдіть швидкість течії, якщо власна швидкість човна становить 12 км/год.
Робітник мав за певний термін виготовити 360 деталей. Перші 5 днів він виготовляв щоденно заплановану кількість деталей, а потім щодня виготовляв на 4 деталі більше й уже за день до строку виготовив 372 деталі. Скільки деталей щодня мав виготовляти за планом робітник?
Висота h (в м), на якій через t секунд виявиться кинуте вертикально вгору тіло, обчислюється за формулою h = V₀ t - 5 t ², де V₀ - початкова швидкість (у м/сек). У який момент часу тіло опиниться на висоті 300 м, якщо за 1 секунду воно піднялося вгору на 75 м?

Розкладання квадратного тричлена

на лінійні множники

Формула

Приклад

Якщо х₁, х₂ – корені тричлена ах²+вх.+с,

то ах²+вх.+с=а(х-х₁)(х-х₂)

Розкладіть на множники квадратний тричлен:

x² – 14x – 32

Розв’язання

1) Знайдемо корені даного тричлена:

x² – 14x – 32 = 0;

x₁ = –2, x₂ = 16.

Отже, x² – 14x – 32 = (x + 2) (x – 16).

Скоротіть дріб

Розв’язання. Розкладемо на множники квадратний тричлен, який є чисельником даного дробу: 6a² – a – 1 = 0;

a₁= a₂₌;

6a² – a – 1= 6 (а+)( а - )= 3(а+)·2( а - )=

( 3a +1 ) (2 a-1 ).

Тоді маємо:

Відповідь:.

I. Найпростіша відтворювальна самостійна робота

Розкладіть на лінійні множники квадратний тричлен:

а)x² – 7x + 12; б) –x² + x + 2; в) b²- b + 1;

г) x² + 8x + 15; д) 6x² – 5x – 1; е) –2x² – 0,5x + 1,5.

Скоротіть дріб:

а) б) в)

II. Реконструктивно-варіативна самостійна робота

Розкладіть на лінійні множники квадратний тричлен:

а)x² + 5x – 14; б) 2a² – 3a + 1; г) 0,3m² – 3m + 7,5;

д) –x² + 3x + 4; е) 4b² – 11b – 3; є) –0,5x2 + x + 1,5.

Скоротіть дріб:

а) б) ; в)

3. Розв’яжіть нерівність:

а) x² + x + 1 > 0; б) (2x – 1) (2x²– 3x + 5) < 0.

4. Спростіть вираз:

а) ; б)

III. Частково пошукова самостійна робота

Розв’яжіть нерівність:

а) –x² + x – 1 0; б) (−5x² + 8x − 5) 0.

2. Знайдіть значення функції:

а) у=; б) .

3. При якому значенні параметра a розклад на лінійні множники тричлена:

а) 2x² – 7x + a містить множник (x – 4);

б) 4x² – ax + 6 містить множник (2x + 1)?

4. Розкладіть на множники многочлен:

а)x² – 6xy + 5y²; б) a² + 5ab – 36b².

IV. Творча, дослідницька самостійна робота

1. Розкладіть на множники многочлен:

а) 3m² – 8mn – 3n²; б) 4x² – 5xy + y²;

в) a² – 14ab + 40b²; г) 12b² + bc – 6c².

2. Скоротіть дріб:

а) б)

3. Доведіть, що при всіх допустимих значеннях a значення виразу не залежить від значення змінної:

а) ; б)

Розв’язування рівнянь, що зводяться до квадратних

Найпростіша відтворювальна самостійна робота

1. Розв’яжіть рівняння: .

Для цього скористайтесь алгоритмом:

а) знайдіть спільний знаменник дробів;

б) помножте обидві частини рівняння на спільний знаменник дробів;

в) складіть рівносильну систему рівнянь, наклавши умову, що знаменник не дорівнює нулю;

г) розв’яжіть систему рівнянь.

2. Розв’яжіть рівняння, заповнюючи пропуски:

= ;

□·□≠0

3.Розв’яжіть рівняння:

а) ; б) 3х+

в) ; г) ;

д) у-10= е)

є) ж)

4.Розв’яжіть рівняння методом заміни змінної, скориставшись алгоритмом:

Позначте х² через t;
Початкове рівняння запишіть, використавши заміну;
Розв’яжіть отримане квадратне рівняння;
Поверніться до змінної х та знайдіть корені початкового рівняння.

а) x⁴ – 5x² + 4 = 0; б) x⁴ – 8x² – 9 = 0;

в) x⁴ – 5x² + 6 = 0; г) x⁴ + 14x² – 32 = 0.

Реконструктивно-варіативна самостійна робота

1.При якому значенні змінної:

а) сума дробів і дорівнює 3;

б) значення дробу на більше за значення дробу ?

2.При яких значеннях а значення дробів рівні: і

3. Розв’яжіть рівняння:

а) 3х+1=;

б) = 3;

в)

4.Розв’яжіть рівняння методом заміни змінної:

а) x⁴ – 29x² + 100 = 0; б) x⁴ + 3x² – 70 = 0;

в) x⁴ – 9x² + 20 = 0; г) 9x⁴ – 10x² + 1 = 0.

III. Частково пошукова самостійна робота

Знайдіть корені рівняння:

а) ;

б) ;

в)

г)

2. При яких значеннях у різниця дробів рівна їх добутку:

3.Розв’яжіть рівняння методом заміни змінної:

а) (x + 3)⁴ – 3 (x + 3)² – 4 = 0;

б) (2x + 1)⁴ – 10 (2x + 1)² + 9 = 0;

в) (6x – 7)⁴ + 4 (6x – 7)² + 3 = 0;

г) (x – 4)⁴ + 2 (x – 4)² – 8 = 0.

4. Розв’яжіть рівняння:

а) (8x² – 3x + 1)2 = 32x² – 12x + 1;

б) (x² – 5x + 7) (x – 2)(x – 3) = 2;

в)

г) .

IV. Творча, дослідницька самостійна робота

Розв’яжіть рівняння:

а) ;

б)

в)

2. При яких параметрах b рівняння :

3.Розв’яжіть рівняння відносно х:

4.Розв’яжіть рівняння:

а) x⁴ + 8x³ + 10x² – 24x + 5 = 0;

б) x⁴ + 4x³ – 10x² – 28x – 15 = 0;

в) 10x² (x – 2)²= 9 (x² + (x – 2)²).

Розв’язування задач

з допомогою раціональних рівнянь

I. Найпростіша відтворювальна самостійна робота

Розв’яжіть задачу, користуючись таблицею:

Знаменник звичайного дробу більший за його чисельник на 3. Якщо до чисельника цього дробу додати 7, а до знаменника 5, то дріб збільшиться на

Заповніть пусті клітинки таблиці, складіть рівняння та знайдіть його корені

Ситуація	Запис дробу і його компонентів через невідоме
Ситуація	Чисельник	Знаменник	Дріб
Було (за умовою)	х	х+3
Стало (після перетворення)

Відповідь: .

Розв’яжіть задачу, користуючись алгоритмом:

Моторний човен пройшов 45 км за течією річки і 22 км проти течії. Знайдіть власну швидкість човна, якщо на шлях за течією річки човен витратив на 1 го більше, ніж на шлях проти течії. Швидкість течії – 2 км/год.

Алгоритм:

Позначте власну швидкість човна х км/год (х>2).
Виразіть швидкість човна за течією річки, якщо швидкість човна х км/год, а швидкість течії річки 2 км/год.
Виразіть час, що човен витратив на шлях за течією, за формулою залежності часу від шлях та швидкості.
Виразіть швидкість човна проти течії річки.
Виразіть час, який човен витратив на шлях проти течії річки.
Запишіть різницю між часом, який човен витратив на шлях проти та за течією.
Складіть рівняння, якщо відомо, що ця різниця дорівнює 1 год.
Розв’яжіть складене рівняння.

Відповідь: 13 км/год, 10 км/год.

Одна бригада працювала на ремонті дороги 7 год, після чого до неї приєдналася друга бригада. Через 2 год спільної роботи ремонт було закінчено. За скільки годин може відремонтувати дорогу кожна бригада, працюючи самостійно, якщо першій для цього потрібно на 4 год більше, ніж другій?

Поїзд запізнювався на 10 хв. Щоб прибути на станцію призначення вчасно, він за 80 км від цієї станції збільшив свою швидкість на 16 км/год. Знайдіть початкову швидкість поїзда.

II. Реконструктивно-варіативна самостійна робота

Водний розчин солі містив 120 г води. Після того як до розчину додали 10 г солі, її концентрація збільшилася на 5 %. Скільки грамів солі містив розчин спочатку?

Розв’яжіть рівняння: 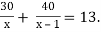Складіть задачу, яка може привести до цього рівняння.

Складіть задачу, розв’язування якої приводить до рівняння

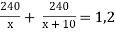
Розв’яжіть цю задачу.

Частково пошукова самостійна робота

Катер пройшов 16 км за течією річки і 30 км проти течії, витративши на весь шлях 1 год 30 хв. Знайдіть власну швидкість катера, якщо швидкість течії становить 1 км/год.

Турист проїхав 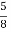всього шляху на катері, а решту — на автомобілі. Швидкість автомобіля на 20 км/год більша за швидкість катера. Автомобілем він їхав на 1 год 30 хв менше, ніж катером. Знайдіть швидкість автомобіля й швидкість катера, якщо всього турист подолав 160 км.

Одному маляру треба на 5 год більше, ніж другому, щоб пофарбувати фасад будинку. Коли перший маляр пропрацював 3 год, а потім його змінив другий, який пропрацював 2 год, то виявилося, що пофарбовано 40 % фасаду. За скільки годин може пофарбувати фасад кожний маляр, працюючи самостійно?

На змаганнях по кільцевій трасі один лижник проходив круг на 2 хв швидше іншого і через годину обігнав його рівно на круг. За скільки хвилин кожен лижник проходив коло?

IV. Творча, дослідницька самостійна робота

Дано двозначне число. Число його одиниць на 3 менше числа десятків. Добуток цього числа на число, записане тими же цифрами в оберненому порядку, дорівнює 574. Знайдіть дане число.

2. Автобус мав проїхати відстань між двома містами, яка дорівнює 400 км, з деякою швидкістю. Проїхавши 2 год із запланованою швидкістю, він зупинився на 20 хв і, щоб прибути у пункт призначення вчасно, збільшив швидкість руху на 10 км/год. З якою швидкістю автобус мав проїхати відстань між містами?

3. Щоб виконати певне виробниче завдання, одному робітникові треба на 12 год менше, ніж другому, і на 4 год більше, ніж обом робітникам для спільного виконання завдання. За скільки годин може виконати це завдання перший робітник?

Література

Бабанський Ю. К. Оптимізація педагогичного процесу. (В запитаннях та відповідях), Київ, 1984.
Методика викладання математики : Практикум/під редакцією Г.П.Бевза/. -К.: „Вища школа” , 1981-198с.
Нільсон О. А. Теорія та практика самостійної роботи учнів. Москва, 1986 р.
Шунда Н.М. Збірник задач з алгебри для 6-8 класів, Київ, 1987 р.
Я.С. Бродський. Математика: Тести для самостійної роботи та контролю знань. – Т.: Навчальна книга- Богдан, 2007-160с.

ЗМІСТ

1.Пояснювальна записка 1

2. Методичні рекомендації 3

3. Неповні квадратні рівняння 6

4. Розв’язування квадратних рівнянь виділенням квадрата

двочлена 10

5. Розв’язування рівнянь за допомогою формули коренів квадратного рівняння 12

6. Теорема Вієта 17

7. Розв’язування задач з допомогою квадратних рівнянь 21

8. Розкладання квадратного тричлена на лінійні множники 24

9. Розв’язування рівнянь, що зводяться до квадратних 27

10. Розв’язування задач з допомогою раціональних рівнянь 31

Алгебра 8 клас, Павлюк Л.П.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Павлюк Людмила Петрівна

Пов’язані теми

Алгебра, 8 клас, Матеріали до уроків

Додано

6 лютого 2018

Переглядів

15810

Оцінка розробки

Відгуки відсутні