Збірник творчих вправ з математики для 3 класу

ЗМІСТ

І. Вступ ……………………………………………………………………………3

ІІ. Нумерація чисел у межах 100 …………………….…………………………4

ІІІ. Додавання і віднімання в межах 100 ……………………………………...7

ІV. Нумерація чисел в межах 1000 ………...………………………..……..….12

V. Додавання та віднімання в межах 1000. Множення та ділення в

межах100………………………………………………………………..……….14

VІ. Логічні задачі …………………………………………….………………….17

VІІ. Задачі з геометричним змістом ……………………………….……...…27

VІІІ. Використана література ………...……………………………………..29

ВСТУП

У навчанні математики особливу роль відведено задачам. З одного боку, вони становлять специфічний розділ програ­ми, матеріал якого учні мають засвоїти, а з другого, висту­пають як дидактичний засіб навчання, виховання і розвитку школярів. Зокрема, у початкових класах задачі є тим кон­кретним матеріалом, за допомогою якого в дітей формуються нові і закріплюються в процесі застосування вже здобуті знання.

Розв'язування задач за певної методики позитивно впливає на розвиток школярів, оскільки потребує вико­нання розумових операцій: аналізу і синтезу, конкретиза­ції і абстрагування, порівняння й узагальнення.

На формування і розвиток умінь молодших школярів розв'язувати задачі відводиться 40—50 відсотків часу, передбаченого навчальним планом на вивчення матема­тики,   причому    насамперед    йдеться   про    арифметичні задачі. Задачі на побудову, найпростіші доведення, а також завдання логічного характеру займають порівняно незначне місце. Саме в такому плані здійснено добір задач у пропо­нованому збірнику: переважна більшість поданих задач є арифметичними, і їх згруповано за основними розділами програми.

Мета цього збірника — дати вчителям початкових класів відповідний додатковий матеріал для роботи на уроці та для позакласної роботи. Вміщені в ньому за­дачі та вправи сприятимуть поглибленню й закріпленню найваж-ливіших програмових питань, а також розвитку ло­гічного мислення і просторових уявлень дітей.

 
                              НУМЕРАЦІЯ  ЧИСЕЛ  У МЕЖАХ 100

1.               Запишіть усі двоцифрові числа, використовуючи цифри 0,3,5. Скільки таких чисел?
2.               Серед усіх двоцифрових чисел, записаних за допомогою цифр 2,4,6,8, скільки таких, що: а) починаються цифрою 4;  б) закінчуються цифрою 8;  в) не починаються цифрою 2?
3.               Іринка записала двоцифрове число однаковими цифрами, а Маринка, яка сиділа навпроти неї, прочитала число, на 33 більше від того, що записала Іринка. Яке число записала Іринка?
4.               На запитання про те, скільки йому років, дідусь відповів: «Мій вік виражається двоцифровим числом, у якого сума цифр дорівнює найменшому двоцифровому числу, а число десятків на шість більше від числа одиниць». Скільки років дідусеві?
5.               Серед двоцифрових чисел, які виражають кількість зошитів, що дав батько кожному зі своїх синів, немає однакових, але в кожному з них сума числа десятків та одиниць дорівнює 5. Скільки було синів у батька та скільки зошитів дістав кожний  з них?
6.               Замість зірочок вставте по одній цифрі в числа  *9, 6*, 6*, 6*  так, щоб кожне наступне число було на 2 одиниці більше від попереднього.
7.               У шафі й на столі разом 93 книжки. Якщо в числі, що виражає кількість книжок у шафі, закреслити цифру одиниць 5, то залишиться цифра, яка позначатиме число книжок на столі. Скільки книжок у шафі та скільки на столі?
8.               Використовуючи кожну із цифр 1,2,3,4,5 по одному разу, запишіть три числа, такі, щоб сума їх дорівнювала 60.
9.               У двоцифровому числі поміняли місцями цифри десятків і одиниць. Виявилося, що різниця між даним і утвореним числами дорівнює 0, а сума – 66. Знайдіть це число.
10.          У двоцифровому числі закреслили ліву цифру 3.  Як змінилося це число?
11.          У запису числа 35 закреслили цифру 5. На скільки одиниць зменшилося це число?
12.          Перелічивши присутніх на дитячому ранку, Андрійко звернув увагу на те, що в двоцифровому числі, яке він дістав, десятків на 4 більше, ніж одиниць, а сума цього числа і числа, записаного тими самими цифрами, але в зворотному порядку, закінчується на 0. Скільки присутніх на дитячому ранку?
13.          Серед двоцифрових чисел, що виражають кількість кілограмів макулатури, зібраної групами учнів  3 класу, немає однакових, і в кожному з них десятків на 6 більше, ніж одиниць. Яке найбільше число груп учнів можливе за цих умов і скільки макулатури зібрано кожною з них?
14.          У новому стоквартирному будинку сім’я Сергійка одержала квартиру №23. Скільки всього в цьому будинку квартир, номер кожної з яких містить у запису принаймні одну цифру 3?
15.          Відстань у метрах, що її проплив Юрко, виражається двоцифровим числом, сума десятків та одиниць якого дорівнює найбільшому одноцифровому числу, причому число десятків на 4 менше від цієї суми. Яку відстань проплив Юрко?
16.          Напиши за допомогою цифр 4, 0, 1 найбільше і найменше трицифрове число. Скільки трицифрових чисел можна записати за допомогою цих цифр?
17.          Від якого трицифрового числа потрібно відняти одиницю, щоб вийшло двоцифрове число?
18.          Напиши трицифрове число, сума цифр якого дорівнює 1 (2, 3).
19.          Запиши всі трицифрові числа, в кожному з яких наступна цифра на 1 більша (менша) від попередньої.
20.          Запиши найбільше і найменше трицифрові числа, в яких всі цифри різні. 
21.          Як зміниться число, якщо до нього праворуч приписати  нуль, два нулі?
22.          Сума двох чисел дорівнює 55. Коли до меншого числа приписати справа 0, то числа будуть рівними. Які це числа?
23.          Телеграфні стовпи розміщені на відстані 50 метрів один від одного. Яка відстань між першим і третім стовпами?
24.          У ряд розміщено 12 стовпів. Відстань між двома сусідніми стовпами     25 м. Яка відстань між крайніми стовпами?
25.          Антон написав на аркуші паперу число 86 і запропонував товаришеві: «Не виконуючи жодних записів збільш це число на 12 і покажи мені відповідь». Товариш миттю здогадався, як треба зробити. А ти  здогадався?
26.          Напиши такі числа замість зірочок, щоб число, яке стоїть над рискою, показувало результат дій:

        28                                           21    

*   • 7                                      *  • 3

*  • 5  + *                                * • 5 + *

* • 6   + *                                 5 • 6 - *

 

16 + *                                     3  • 8 - *

2 • *                                         * + * + *

* + * + * + *                           * • 9 + 3

2 • * + 2 • *                             2 • 8 + *

 

 

ДОДАВАННЯ  І  ВІДНІМАННЯ  В МЕЖАХ 100

1.   Яке число в натуральному ряді дорівнює сумі всіх попередніх чисел ?
2.   Подайте число 20 за допомогою: а) трьох однакових чисел;   б) трьох однакових цифр.
3.   На вулиці гралося 12 дітей. Хлопчиків було більше, ніж дівчаток. Скільки могло бути хлопчиків і скільки дівчаток?
4.   У кожного з п’яти хлопчиків було не менше однієї кульки, а всього в них було 7 кульок. Чи міг хтось із хлопчиків мати 3 кульки, 4 кульки?
5.   На скільки сума двох доданків більша від першого з них?
6.   На скільки зменшуване більше від різниці?
7.   На скільки від’ємник менший від зменшуваного?
8.   Знайдіть три числа, якщо сума будь-яких двох з них на 7 більша від третього.
9.   Знайдіть два числа,  якщо одне з них більше від другого на 15, а сума їх більша від одного з доданків на 20.
10.  Знайдіть суму двох чисел, якщо вона на 25 більша від одного доданка і на 32 більша від другого.  Зменшуване 17, від’ємник 8. До від’ємника додали різницю цих чисел. Взявши утворене число за новий від’ємник і залишивши те саме зменшуване, знайдіть нову різницю.
11.  Працюючи в саду, на городі діти зібрали 7 ящиків огірків, 12 ящиків помідорів, 9 ящиків груш і 11 ящиків яблук. Чого більше вони зібрали – овочів чи фруктів – і на скільки? (Усі ящики однакові).
12.  Коли Дмитрик подарував Віті 7 марок, то в  хлопчиків стало по 15 марок. Скільки марок було спочатку в кожного з хлопчиків?
13.  До годівниці спочатку прилетіло 15 горобців, а потім синиці. Горобців було на 5 менше, ніж синиць. Скільки прилетіло синиць?
14.  На луці паслися вівці, кози, коні та корови. Овець було 3, стільки ж кіз, а коней менше, ніж кіз, але більше ніж корів.  Скільки всього паслося тварин?
15.  Якими мають бути числа a  і  b, щоб можна було відняти  b від a   і  a  від  b?
16.  У виразі  1*2*3*4*5*6*7*8*9  замість зірочок поставте знаки «+» і  «-» так, щоб після виконання дій дістати число 1.
17.  Під час гри Михайлик пробіг в одному напрямі 45 метрів, а потім повернувся і пробіг у протилежному напрямі 60 метрів. На якій відстані від стартової лінії він опинився?
18.  По стовбуру повзе жук. За ніч він піднімається на 6 м, а за день опускається на 3м. Почавши повзати від основи стовбура, за п’яту ніч він досягає його вершини. Яка висота стовбура?
19.  Коли батькові було 28 років, синові було 5 років. Тепер батькові 35 років. Скільки років синові?
20.  На уроці фізкультури хлопчики вишикувалися в шеренгу, і Миколка побачив, що він восьмий зліва і шостий справа. Скільки хлопчиків було в шерензі?
21.  Знайдіть число, яке більше від 11 на стільки, на скільки воно менше від 17.
22.  Коли Юрко закінчив читати 53 сторінку книжки, то звернув увагу на те, що перша з прочитаних сьогодні сторінок має номер, відмінний від 53, але записаний тими самими цифрами. Скільки сторінок він сьогодні прочитав? 
23.  У двох перших класах учнів було порівну. Двох учнів з 1 –А  перевели у    1 – Б. У якому класі стало учнів більше і на скільки?
24.  У двох дівчаток зошитів було порівну. Коли перша з них віддала другій кілька зошитів, то в другої стало на 6 зошитів більше, ніж у першої. Скільки зошитів віддала перша дівчинка другій?
25.  9 л молока налили у дванадцятилітрову посудину, наповнили семилітрову. А потім у дванадцятилітрову долили молоко із семилітрової. Скільки літрів молока залишилося у семилітровій посудині?
26.  У двох ящиках було 15 кг яблук. Коли з другого ящика взяли 3 кг яблук, то в ньому залишилося 7 кг. Скільки кілограмів яблук було в першому ящику?
27.  Потрібно було відремонтувати 28 вантажних і легкових автомобілів. За тиждень відремонтували усі вантажні та 7 легкових автомобілів, після чого залишилося відремонтувати 8 легкових. Скільки було вантажних автомобілів?
28.  Для поливання шкільної ділянки було заготовлено 2 баки води: в одному 45 відер, у другому – 33. За один і той самий час з кожного бака води забирали порівну. Скільки воли залишилося в другому баці, якщо в першому залишилося 18 відер?
29.  Розподіліть числа 2,3,4,5,6,7,8 на дві групи так, щоб сума двох будь-яких чисел в одній групі не дорівнювала жодному числу другої групи.
30.  Розподіліть числа 2,3,4,5,6,7,8 на дві групи так, щоб різниця  будь-яких чисел у кожній  групі не дорівнювала жодному числу цієї групи.  Чи можна це зробити з числами 1,2,3,4,5?
31.  У наведених нижче таблицях числа записані за певною закономірністю. Установіть цю закономірність і знайдіть числа, які потрібно записати замість трьох крапок.

                  а) 4  2  6                                                   б) 8  1  7

                      1  8  9                                                        3  2  1  

                      7  3  …                                                      6  2  …

32. Числа четвертого стовпчика утворено в результаті виконання дій над числами перших трьох стовпчиків. За результатами двох перших рядків знайдіть правило, за яким дістають числа четвертого стовпчика, та заповніть порожні клітинки.

25	5	10	20
22	13	5	30
18	7	15
12	34	25

 

32. На дошці було записано рівні суми та рівні різниці. Під час перерви деякі цифри випадково витерли. Вони позначені зірочкою. Відновіть ці цифри.

а) 6* + 23 = *7 + 38;                                     б) *0 + 35 = 3* + 56

в) 50 - * = *3 – 13                                          г) 30 – 3* = *3 – 13

33. Сума трьох чисел дорівнює їхньому добутку. Числа ці різні і одноцифрові. Назвіть ці числа.

34. У кожному виразі постав дужки так, щоб його значення збільшилось.

       3 + 4 • 8                    24 – 18 : 2 + 4                        24 : 6 – 2

       32 : 8 – 4                   42 – 24 : 3 + 3                        7 • 3 + 4

35. Де треба поставити дужки, щоб вираз мав відповідне числове значення?

       24 – 4 •   3 + 2 = 10                             24 – 4  •  3 + 2 = 4

       24 – 4  •  3 + 2 = 12                             24 – 4  •  3 + 2 = 100

36. Знайдіть два числа. У кожному з яких число цифр у його записі дорівнює числу букв у слові, що є його назвою.

37. Запишіть число 100 за допомогою усіх цифр від 0 до 9 і знаків дій.

38. Запишіть число 100 п’ятьма трійками. 

39. Знайдіть найраціональнішим способом суму всіх чисел від 1 до 20.

40. Одне з чисел у ряді 2; 6; 18; 162; 54 переставте так, щоб в утвореному ряді всі числа були розташовані в певному порядку. Як відрізняється наступне число від попереднього?

41. У кружечках, поданих на малюнку, розставте всі числа від 1 до 7 (кожне по одному разу) так, щоб сума чисел, розміщених вздовж кожного відрізка, була однією й тією ж самою.

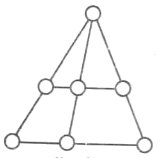
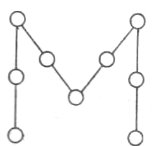
42. У кружечках, поданих на малюнку, розставте всі числа від 1 до 9 (кожне по одному разу) так, щоб сума чисел, записаних вздовж  кожного з чотирьох відрізків фігури (букви М), були рівними між собою і найменшими з можливих.

43. Один рибалка розповідав, що він піймав рибу, хвіст якої мав масу 2 кг, тулуб – таку саму масу, як хвіст і голова разом, а дві голови  - таку, як тулуб і два хвости разом. Яка маса всієї рибини?

44. У кімнаті стояло кілька стільців на 4-х ніжках і табуреток на 3-х ніжках. Скільки було стільців і скільки табуреток, якщо всього 17 ніжок?

45. 5 другокласників і 7 третьокласників купили 50 зошитів. Знаючи, що кожний учень одного класу купив однакову кількість зошитів, але не таку, як учень іншого класу. Визначте, скільки зошитів купив кожний другокласник і кожний третьокласник.

46. Мишко живе в дев’ятиповерховому будинку, в якому перший поверх першого, другого і третього під’їздів займає магазин. На якому поверсі і в якому під’їзді живе Мишко, якщо номер його квартири 63, а на кожній площадці 4 квартири?

47. Миші до нірки 20 кроків, а кішці до неї 5 стрибків. Поки кішка зробить один крок, миша зробить 3 кроки, а один стрибок кішки дорівнює за довжиною 10 крокам миші. Чи наздожене кішка мишу?

48. У трьох купках є відповідно 11, 7  і  6  зошитів. Потрібно трьома перекладаннями  зрівняти кількість зошитів в цих купках, причому з будь-якої купки дозволяється перекладати в іншу лише стільки зошитів, скільки в ній вже є. Як це зробити?

49. Від початку доби минуло 60 год. Яка це частина доби?

50. Від початку доби минуло 31 год.   Котра зараз година?

51. Що більше: сума чисел 0 + 1 + 2 + 3 + 4 + 5  чи добуток  0 •1•2• 3 • 4 • 5 ?

52. Дано три числа: 1, 2, 3. Змінюючи коми знаками дій і не змінюючи порядку розміщення чисел, можна дістати одиницю, тобто (1 + 2) : 3 = 1. Спробуй дістати одиницю з таких груп чисел: 1, 2, 3, 4;  1, 2, 3, 4, 5, 6.

 

НУМЕРАЦІЯ ЧИСЕЛ В МЕЖАХ  1000

1.   Один хлопчик сказав, що в їхньому будинку номери десяти квартир виражаються двоцифровими числами, які закінчуються на 0,  а другий відразу ж заперечив: «Такого не може бути!» Яку підставу він для цього мав?
2.   Знайдіть трицифрове число, у якому кожна наступна цифра на 1 більша від попередньої. Скільки може бути різних відповідей?
3.   Запишіть у порядку зростання трицифрові числа, у кожному з яких  у розряді одиниць стоїть цифра 5, а в розряді сотень – цифра 2. На скільки найбільше число більше від найменшого?
4.   Серед трицифрових чисел, які позначають кількість виробів, виготовлених за певний час кожною бригадою, немає однакових, але в кожному з них сума числа сотень, десятків та одиниць дорівнює 3. Яке найбільше число бригад може бути і скільки виробів виготовила кожна з них?
5.   Коли Оленка й Віра побачили, що на світловому табло в числі 25 погасла цифра 5, Оленка зауважила, що такий самий результат можна дістати, якщо від 25 відняти 5. Віра заперечила їй. Хто з дівчаток правий?
6.   До даного двоцифрового числа ліворуч приписали цифру 5. На скільки при цьому  збільшилося число?
7.   У трицифровому числі закреслили крайню зліва цифру 7.  Зменшилося чи збільшилося число і на скільки?
8.   У числі 325 закреслили цифру 2. На скільки зменшилося при цьому число?
9.   Сума двох чисел 66. Якщо до меншого приписати праворуч 0, то числа стануть рівними. Знайдіть ці числа.
10.  Два десятки помножити на три десятки. Скільки десятків отримаємо?
11.  Півсотні зошитів роздали учням, по півдесятка кожному. Скільки учнів дістали зошити?
12.  Знайдіть  таке двоцифрове число, записане різними цифрами, щоб сума його з двоцифровим числом, здобутим у результаті переставляння цифр у шуканому, була: а) найбільшою; б) найменшою. У кожному випадку обчисліть згадану суму.
13.  Знайдіть двоцифрове число, при діленні якого на суму його цифр дістаємо число, що дорівнює дільнику.
14.  Знайдіть двоцифрове число, у якого добуток цифр дорівнює  найбільшому одноцифровому числу і число десятків менше, ніж число одиниць.
15. Записали  двоцифрове число, а потім перевернули  аркуш паперу  із записаним числом так, що верхня і нижня  половини аркуша помінялися місцями. При цьому виявилося, що число не змінилося. Яке число було записано?
16.  Тетянка записала на аркуші паперу число 666 і запропонувала своїй подрузі Галинці збільшити це число на 333, не виконуючи арифметичних дій і нічого не записуючи. Галинка відразу ж зміркувала, як це робити. Як міркувала Галинка?
17.  Відповідаючи на запитання про те, скільки йому років, дідусь сказав:          « Якщо від найбільшого трицифрового числа віднімете 91 десяток, то дістанете на 12 одиниць більше за мій вік». Скільки дідусеві років ?
18.  За допомогою дужок  вкажи порядок дій, за якого відповіді будуть правильними:

           160 – 20 + 70 = 70                              370 – 60 + 40 =350

            140 – 80 + 30 = 30                              210 + 70 – 90 =190

19. Не виконуючи дії, скажи, на скільки сума 118+110+112 більша за суму 117+109+111?

20. Сума номерів трьох будинків, що стоять поруч по один бік вулиці, дорівнює 117. Визначте ці номери.

21. Скільки серед чисел від 100 до 1000 включно таких, у запису яких зустрічаються три однакові цифри?

22. У залі для глядачів 500 місць. У кожному ряді однакове число місць, причому більше, ніж рядів у залі. Якщо в кожному з чисел, що виражають кількість рядів і кількість місць, закреслимо по одній справа цифрі, то дістанемо рівні між собою числа. Скільки в залі рядів та скільки місць в кожному ряді?
                      ДОДАВАННЯ ТА ВІДНІМАННЯ В МЕЖАХ 1000.

МНОЖЕННЯ І ДІЛЕННЯ В МЕЖАХ 100

1.   Напиши число 1000 за допомогою семи одиниць та знаків дій.
2.   Число 125 подати за допомогою трьох однакових чисел та дій додавання і віднімання.
3.   Число 300 подати у вигляді двох чисел, використавши п’ять однакових цифр.
4.   Микола зібрав у коробку павуків і жуків – усього 8 штук. Якщо підрахувати, скільки ніг у коробці, то їх налічується 54. Скільки у коробці павуків і скільки жуків?
5.   Назви двоцифрові числа, після зменшення яких у два рази утворюється знову двоцифрове число, але з однаковими цифрами.
6.   Знайдіть усі двоцифрові числа, кожне з яких можна подати у вигляді добутку трьох однакових множників.
7.   За допомогою ста десятків і знаків дій запишіть тисячу.
8.   Скільки буде, якщо двоцифрове число, записане вісімками, поділити на двоцифрове число, записане двійками.
9.   Якщо від деякого трицифрового числа відняти двоцифрове число, дістанемо 111. Якщо у зменшуваному закреслити цифру одиниць 3, то дістанемо від’ємник. Знайдіть ці числа.
10. Поставте замість зірочок знаки дій:

а) 3 * 2 * 1 = 1;                б) 1 * 2 * 3 * 4 = 4.

11. Як, використовуючи 4 рази цифру 5, знаки дій і дужки, дістати число 100?

12. Використавши тричі цифру 5, знаки дій і дужки, запишіть:

    а) найбільше можливе число;     б) найменше можливе число.

13. Як за допомогою п’яти двійок і знаків дій дістати число 7?

14. Запишіть число 37 за допомогою п’яти трійок і трьох знаків дій.

15. Запиши чотирма трійками і потрібними знаками дій всі числа від 5 до 10.

16. Напиши всі числа від 1 до 10 за допомогою чотирьох четвірок і знаків дій.

17. За допомогою п’яти п’ятірок і потрібних знаків дій запиши числа 10 і 100.

18. Як записати нуль трьома п’ятірками?

19. Напиши число 10 однією цифрою, яка повторювалася б 5 разів.

20. За допомогою п’яти двійок і потрібних знаків дій напиши числа від 1 до 10.

21. Склади приклади на додавання, віднімання, множення і ділення з однаковим результатом.

        Зразок.   67+ 53 = 120,       485 – 365 = 120,

                       15• 8 = 120,          1200 : 10 = 120.

22. У скільки разів збільшиться одноцифрове число, якщо його помножити на 10 і додати це одноцифрове число?

23. У скільки разів збільшиться одноцифрове число, якщо його помножити на 10 і відняти це одноцифрове число?

24. Підберіть числа, для яких зміна знака додавання на знак множення не змінює результат.

     Зразок.      1 + 2 +3 = 1 •2 • 3 = 6.

25. Чи можна поділити три апельсини між двома батьками і двома синами так, щоб кожному дісталося по апельсину?

26. Якщо частка від ділення двох чисел дорівнює одиниці, то яка різниця цих чисел?

27. а) На яке найбільше число ділиться без остачі будь-яке число?

       б) На яке найменше число ділиться будь-яке число без остачі?

        в) Яке число ділиться без остачі на всі числа?

28. З чисел 2, 3, 5, 7, 11, 17, 19, 38 виберіть ділене, дільник, частку й остачу.

29. Запишіть у вільні клітинки квадрата числа 12 і 13 так, щоб по всіх лініях (горизонтальних, вертикальних і «з кута на кут») дістати в сумі 36.

	11
11
		11

 

30. На двох острівцях сиділо 119 чайок. Коли з одного острівця 15 чайок полетіло в море, а 12 перелетіло на другий острівець, то на обох острівцях чайок стало порівну. Скільки чайок було на кожному острівці спочатку?

31. В автобусі їхало 40 дорослих пасажирів. На зупинці вийшло 7 чоловіків та 5 жінок, після чого в ньому стало чоловіків і жінок порівну. Скільки чоловіків і скільки  жінок було в автобусі спочатку? 

33. Троє рибалок вирішили усю пійману ними рибу розділити порівну. Один з них піймав 17 рибин, другий -12, а третій – 10. Хто, кому і скільки рибин має віддати?    
34.  В сім’ї троє дітей: Тетянка, Світланка і Юрко. Юрко молодший за Світланку, а Тетянка старша за Світланку на 3 роки. Скільки років кожному, якщо їм разом 27 років?
35.  Батькові 39 років, а синові 14.Скільки років дочці, якщо через 16 років синові та дочці разом буде стільки років, скільки батькові?
36.  На питання щодо свого віку Сашко відповів: «Мені разом із сестрою 22 роки, а 7 років тому я був втричі старший  за неї». Скільки років Сашкові?
37.  Є дві коробки, одна з яких вміщує 300 г, а друга – 650 г крупів. Як за допомогою цих коробок відсипати 1 кг крупів?     

ЛОГІЧНІ ЗАДАЧІ

1. На вулиці в чотирьох сусідніх будинках живуть два хлоп­чики та дві дівчинки: Катруся, Марічка, Петрик і Василь. У кожного є хобі. Визнач, хто в якому будинку мешкає і в кого яке хобі, якщо:

•   у будинку Катрусі більше ніж три вікна;
•   у будинку Петрика менше ніж п'ять вікон;
•   один із хлопчиків полюбляє кататися на скейті (роликовій дошці);
•   номер будинку Марічки менший за цифру 17;
•   у будинку номер 13 живе дівчинка, яка зай­мається балетом;
•   Катруся не любить плавати;
•   два   хлопчики,   Петрик   і   Василь,   мешкають у сусідніх будинках;
•   Марічка не любить танцювати;
•   той,  хто  мешкає поряд із  Петриком,  ходить у басейн;
•  
  той, у кого двері в будинку розташовані по­середині, любить малювати.

 

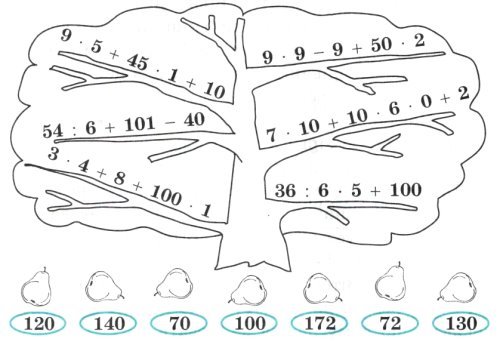
2. Розв'яжи приклади, які розміщені на гілках груші. За відповідями визнач, з якої гілки кожна груша. Яка з груш зайва? Закресли її.

 

 

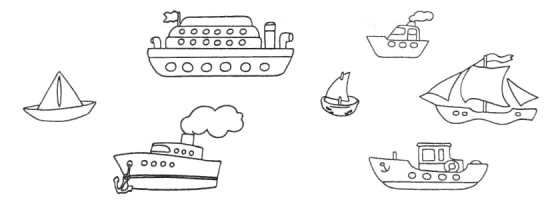
3. Як розділити малюнок трьома лініями так, щоб кожний корабель був відокремлений від інших?

4. Замок займає чверть усієї території маєтку. Реш­ту території займає парк. Чотири родини купили за­мок, і кожна сім'я хоче, щоб у неї була власна части­на парку. Усі частини парку повинні бути однаковими за розміром, і в кожній частині повинні бути ставок, дерево і лавка. Розділи парк між родинами.

5. Родина  Іванових їде відпочивати.  Але всі члени  родини вирушають до різних місць.

•     Виїзд із будинку о 8 ранку.
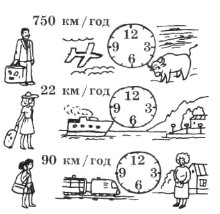•     Тато летить до Іспанії літаком за 1500 км від будинку.
•     Мама пливе на кораблі за 66 км від будинку.
•     Рита їде потягом до тітки

за 360 км від будинку.

Познач на годиннику час прибуття на місце відпочинку кожного члена родини Іванових.

6. Ким працюють тата хлоп'ят і які тварини живуть у них удома, якщо:

•     тато Саші — пекар;
•     у Ганни немає кішки;
•     Саша дуже любить свого собаку;
•     у тата Юлі немає машини;
•     в одного з хлопчиків є черепаха;
•     у шофера немає синів;
•     Юля не дочка вчителя;
•     Юлина кішка чорного кольору;
•     у листоноші є дочка.

Запиши відповіді в таблицю.

 

	Саша	Рома	Ганна	Юля
Собака
Кішка
Канарка
Черепаха
Пекар	+	—	—	—
Шофер
Учитель
Листоноша

 

 

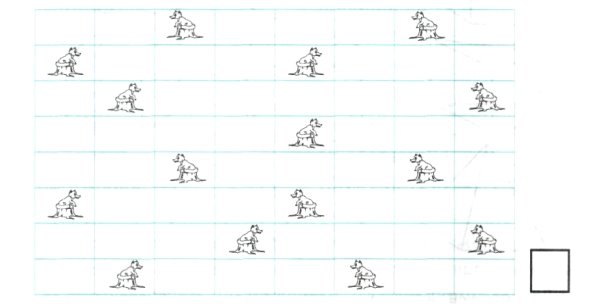
7. Розв'яжи задачу.

У лісі на пеньках розмістилися 15 хитрих ли­сиць. Скільки зайців можуть сміливо сидіти під ку­щами, якщо лисиці здатні помітити довговухих тільки на відстані сусідніх клітинок по горизонталі або вертикалі?

 

 

 

 

 

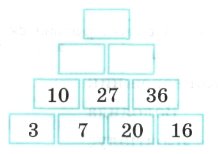
8. Встанови закономірність і визнач, які числа мають бути в порожніх квадра­тах. Запиши їх.

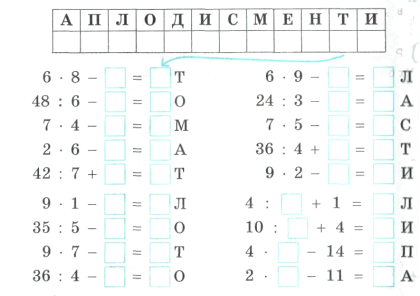
9. Пронумеруй за порядком букви в слові аплодисменти і впиши відповідні цифри в квадратики поряд із буквами Віднови приклади.

 

10. Розділи коло на чотири рівні частини так, щоб сума чи­сел у кожній частині дорівнювала 13.

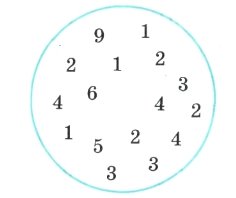
11. Впиши у вільні клітинки 0, 1 або 2 так, щоб сума чи­сел по горизонталі, вертикалі та діагоналі дорівнювала 3.

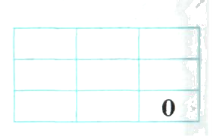
12. Розплутай головоломку. Сума чисел по вертикалі та по горизонталі має дорівнювати 10. Ти можеш ви­користовувати числа 1, 2, 3, 4, 5, 6, 7. Кожне число в кожному конкретному випадку ти можеш використа­ти лише один раз.

 

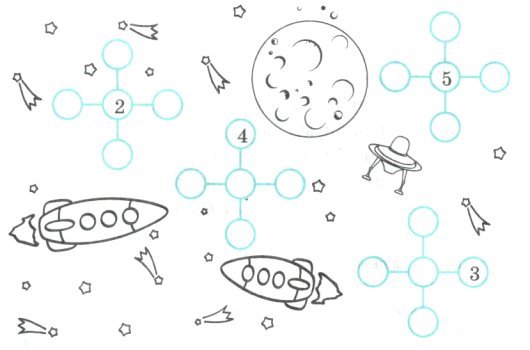
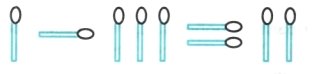
13. На малюнку є помилка: один мінус три не може дорівнювати двом. Але спробуй перемістити всього один сірник,  і дія буде виконана правильно.

14. Тітка Катерина шукає номер телефону свого племінника. Допоможи їй. Тобі відомо, що:

•     Перше число дорівнює четвертому числу.
•     Друге число дорівнює третій частині восьмого числа.
•     Третє число  дорівнює сумі п'ятого,  шостого і сьомого чисел.
•     Четверте число дорівнює 4 + 1 + 2-3-4.
•     П'яте число на одиницю більше за четверте.
•     Шосте число дорівнює трьом.
•     Сьоме число дорівнює п'ятому числу.
•     Восьме число втричі більше за шосте число.
•     Дев'яте число дорівнює восьмому мінус три.
•     Десяте число у два рази більше за друге.

 

 

15. Впиши в кожний кружечок 1, 2 або 3 так, щоб сума чи­сел по горизонталі, вертикалі та діагоналі була однаковою. Пам'ятай: в усіх кружечках по­винні бути однакові цифри.

 

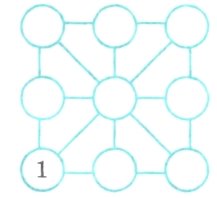
16. Котра тепер година, якщо від початку доби минуло в два рази менше часу, ніж залишилося до її кінця?

17. Котру годину показує годинник, коли обидві його стрілки  спрямовані в протилежні боки і показують ціле число годин?

18. Якщо о 12 год  дня йде дощ, то чи можна  чекати, що через 36 год  буде сонячна погода?

19. У порожні клітинки впиши відповідні цифри так, щоб усі чотири приклади було розв'язано правильно. Жодна з цифр не повинна повторюватися.

 

20. Котра тепер година, якщо від восьмої години ранку минула третина того часу, що залишився до дванадцятої години ночі?

21. Який зараз день і котра година, якщо від дев’ятої години суботнього вечора до теперішнього часу хвилинна стрілка зробила рівно 40 обертів?

22. У дівчинки стільки ж братів, скільки й сестер, а в хлопчика з цієї сім'ї братів немає. Скільки в цій сім'ї хлопчиків і скільки дівчаток?

23. У батьків було 3 дочки, у кожної з них було по 2 брати. Скільки всього дітей у цій сім'ї?

24. Дідуся звуть Григорій Васильович, його онука — Андрій Віталійович. Як звуть батька онука?

25. Двоє батьків, двоє синів та дідусь з онуком піймали по 6 окунів, а всього 18. Як це могло статися?

26. У сім'ї троє дітей: Андрійко, Маринка і Галинка. їм відповідно 5, 8 і 13 років. Скільки років кожному з них, якщо одна дівчинка ходить до дитячого садка, а Маринка старша за Андрійка?

27. У Юрка було 13 зошитів а в Андрійка 10. У кожної з двох дівчаток — Оленки та Тетянки зошитів було більше, ніж у одного з хлопчиків, але менше, ніж, у другого, причому більше було в Тетянки. Скільки зошитів було в кожної дівчинки?

28. Троє хлопчиків — Мишко, Сергійко та Сашко живуть в одному під'їзді на різних поверхах; п'ятому, сьомому та восьмому. Михайлик живе не нижче за Сашка, а Сергійко — не вище за Сашка. Хто з хлопчиків на якому поверсі живе?

29.  На столі між ручкою і олівцем лежить лінійка. Чи можна, не перекладаючи її, зробити так,  щоб вона   стала крайньою?

30.  З коробки, у якій 7 червоних і 5 синіх олівців, на­вмання беруть олівці. Яке найменше число олівців треба взяти, щоб серед них було не менш як два червоних і не менш як три синіх?

31.  У ящику лежать 12 білих і 9 чорних кульок, які від­різняються тільки кольором. Яку найменшу кількість ку­льок, беручи їх навмання, треба взяти, щоб серед них бу­ло не менш як 6 однакових за кольором?

32.  3 яблука і 1 диня врівноважують 10 персиків, а 6 персиків і 1 яблуко врівноважують 1 диню. Скільки потрібно взяти персиків, щоб урівноважити  1   диню?

33.  Назвіть 5 днів підряд, не вживаючи чисел та назв днів тижня.

34. Чотири катери «Альбатрос», «Бригантина», «Ви­хор» та «Глобус» — відходять від причалу в різний час. «Альбатрос» відходить не першим, але раніше за «Вихор» та «Глобус», а «Глобус» не раніше за «Вихор». Розмістіть назви катерів, у тому порядку, у якому вони відходять від причалу.

35. Четверо хлопчиків — Дмитрик, Сашко, Ігор і Петрик — змагалися з бігу. Після закінчення змагань кож­ного запитали, яке місце він зайняв. Дмитрик відповів: «Я був не першим і не останнім». Сашко сказав: «Я був не останнім». Ігор: «Я був першим». Петрик: «Я був останнім». Три з цих відповідей правильні, а одна — ні. Хто був першим?  Хто був останнім?

36.   Переставте одне число в ряді 20, 17, 14, 5, 11, 8, 2, так, щоб усі числа були розташовані в певному порядку.

37.  Спостерігаючи за світлофором біля свого будинку, Сергійко за деякий час нарахував, що червоне світло спала­хувало 20 раз. Скільки за цей час (тобто між першим і останнім спалахом червоного) засвічувалося зелене світло і  скільки  жовте?

38. Четверо хлопчиків — Василько, Петрик, Сашко та Юрко, грали у перетягування каната. Юрко і Петрик легко перемогли Сашка з Васильком. Проте коли Юрко став у парі із Сашком, то вони мало не програли Василькові з Петриком. Коли ж Юрко з Васильком змагалися з Петриком та Сашком, то ніяка з цих пар не змогла перемогти іншу.  Як розподіляються хлопчики за своєю силою?

39. У сім'ї четверо дітей: Сергійко, Іринка, Івась та Галинка. їм 5, 7, 9 і 11 років. Скільки років кожному з них, якщо один з хлопчиків ходить у дитячий садок, Іринка молодша за Сергійка, а сума років дівчаток ділиться на 3?

40. На одній будові працюють муляр, тесляр та маляр, їхні прізвища Борисенко, Іваненко, Петренко. У муляра нема ні братів, ні сестер і він менший за всіх на зріст. Петренко одружений із сестрою Борисенка і вищий на зріст за тесляра. Назвіть прізвища муляра, тесляра та маляра.

41. Майстер спорту Сивенко, кандидат у майстри Чорненко і першорозрядник Руденко зустрілися в клубі перед початком турніру. «Зверніть увагу, — сказав чорноволосий,— один з нас сивий, другий рудий, а третій чорноволо­сий, але ні в кого колір волосся не відповідає його прізвищу. Цікаво, чи  не правда?»

«Ти правий»,— зауважив майстер спорту. Якого кольору волосся у кандидата в майстри?

42. Як, маючи дві посудини на 9 л і 4 л, принести з річки 6 л води?

43. З трьох однакових за зовнішнім виглядом кульок одна легша кожної з решти. Як одним зважуванням на шалькових терезах без гир знайти легшу  кульку?

44. Як за допомогою шалькових терезів без гир відважити 14 кг цукру, якщо в торбинці є 16 кг цукру?

45. У ящику є 8 кг круп. Потрібно за допомогою терезів з шальками і двох гир по 200 г відважити 1 кг 900 г крупів. Як це зробити за допомогою не більш як двох зважувань?

46. Сергійко стверджував, що в цьому році буде місяць з п'ятьма неділями та п'ятьма середами. Чи правий він?

ЗАДАЧІ   З   ГЕОМЕТРИЧНИМ   ЗМІСТОМ

1.   Поділіть трикутник на: а) 2 трикутники; б) трикутник і чотирикутник.

2.  Поділіть  п'ятикутник  на 3 трикутники.

3. У п'ятикутнику всі вершини сполучено відрізками прямих (з кожної вершини проведено 2 відрізки). На скільки частин поділився при цьому п'ятикутник? Які фігури є серед них? Скільки фігур кожного виду?

4. Двома відрізками поділіть чотирикутник на 3 частини так, щоб: а) усі вони були чотирикутники; б) усі вони були трикутники; в) один був чотирикутник і 2 трикутники; г) один був трикутник і 2 чотирикутники.

5. Двома відрізками поділіть чотирикутник на 4 частини так, щоб серед них були: а) усі трикутники; б) 2 трикутники і 2 чотирикутники; в) 2 трикутники і 2 п'ятикутники; г) 3 трикутники і 1 чотирикутник.

6. Із семи однакових паличок складіть 3 трикутники.

7. Із шести однакових паличок складіть квадрат і трикутник.

8. Полічіть, скільки всього трикутників на малюнку.

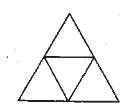
9. Яке найменше число однакових паличок треба узяти, щоб скласти один квадрат; два квадрати; три квадрати?

10. Є аркуш паперу. Як розрізати його на 5 частин одним розрізом?

11. Порівняйте кількість трикутників у кожній з фігур, зображених на малюнку.

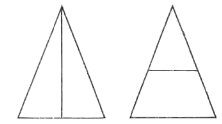
12.  Скільки всього квадратів зображено на малюнку?

 

13.   На які фігури може поділити пряма лінія прямо­кутник?

14.  Сторони прямокутника 3 см і 2 см. Поділіть його на З квадрати.

15.  Скількома способами можна з прямо­кутника, довжина якого 6 см і ширина 2 см, скласти новий прямокутник, розбивши да­ний на дві частини одним прямолінійним розрізом?

16.  5 точок розмістіть по 3 на кожному з двох відрізків.

17. Яке найбільше число прямих кутів може мати чоти­рикутник, що не є прямокутником?

18.  Відомо, що в даному прямокутнику дві сторони, які утворюють прямий кут, мають однакові довжини. Чи є цей прямокутник квадратом?

19.  Є три прямокутники: довжина і ширина першого 7 см і 3 см; другого —     4 см і 2 см; третього — 5 см і 4 см. Чи можна із цих прямокутників скласти   квадрат?

20.  Є три квадрати: довжина сторони першого 6 м, дру­гого — 3 м, і третього теж 3 м. Чи можна із цих квадратів скласти прямокутник?

21.  З п'яти однакових паличок складіть два трикутники і один чотирикутник.

22.  З десяти однакових паличок складіть: а) два квад­рати; б) три квадрати.

23. 3 десяти однакових паличок складіть три квадрати так, щоб, вилучивши 2 палички, можна було дістати 2 квадрати.

24. Уздовж межі ділянки квадратної форми потрібно посадити 10 тополь, порівну вздовж кожної сторони. Як це зробити?

25. Квадрат можна розрізати на 4 однакові частини. Розріжте квадрат на 5 одна­кових частин.

28.  Замкнена ламана лінія складається з чотирьох від­різків.  Які фігури вона може утворювати?

ВИКОРИСТАНА ЛІТЕРАТУРА

1. Лісіцина І.С. Математика: Різнорівневі завдання. 4 клас / І.С. Лісіцина — Х: Торсінг плюс, 2006. – 64 с.

2. Гришко А.А. Розвивальні завдання для початкової школи: Робочий зошит для 3 класу / А.А. Гришко, А.І. Лазарєва  — Х.: Видавництво «Ранок», 2010. – 64 с.

3. Друзь Б.Г. Творчі вправи з математики для початкових класів: Посібник для вчителів / Б.Г. Друзь – К: Рад. шк., 1998. — 144 с.

4. Клименченко Д.В. Збірник вправ з математики для початкових класів: Метод. посібник / Д.В. Клименченко. — К.: Рад. шк., 1987. – 96 с.