Збірник задач для підготовки учнів до олімпіади з Інформатики
Управління освіти
виконавчого комітету Ковельської міської ради
Міський методичний кабінет
Комунальний заклад «навчально-виховний комплекс «загальноосвітня школа І-ІІІ ступенів № 13 – колегіум» міста Ковеля»
Номінація:
Інформатика
Збірник задач з програмування
2018 р.
Відомості про автора:
Ковальова Світлана Ярославівна, спеціаліст першої категорії, стаж 17 років.
Рецензенти:
1. Прилепа Н.П.– заступник директора з навчально-виховної роботи
Анотація:
Збірник містить задачі, які можна використовувати під час проведення уроків для засвоєння теми програмування та для підготовки учнів до олімпіади з інформатики.
Вчителі та учні мають змогу ознайомитися з завданнями та розв’язками основних типів задач з програмування в програмному середовищі Pascal.
Матеріали схвалено на засіданні методичної ради
Комунального закладу «НВК «ЗОШ І-ІІІ ст. № 13 – колегіум» м. Ковеля»
Протокол №7 від 10.02.2018р.
Голова методичної ради С.А .Філіпчук
ЗМІСТ
ВСТУП ……………………………………………...4
РОЗДІЛ 1. ОСНОВНІ ТИПИ ЗАДАЧ …………….5
1.1. Лінійні програми ………………………............6
1.2. Програми з розгалуженням ………………….10
1.3. Цикл з параметром ……………………………29
1.4. Цикл з передумовою ………………….............38
1.5. Цикл з післяумовою …………………………..47 1.6. Вказівка вибору ……………………….............58
РОЗДІЛ 2. ЗАДАЧІ ІІ ЕТАПУ ВСЕУКРАЇНСЬКОЇ ОЛІМПІАДИ З ІНФОРМАТИКИ ………………………...65
2.1. 2016-2017 рік …………………………..............66
2.2. 2017-2018 рік …………………………..............75
Список використаних джерел ……………………..86
ВСТУП
Збірник містить практичні матеріали для використання як і на уроках інформатики так і для самоподготовки. Деякі задачі містять коротке пояснення до розв’язання. До нього ввійшли задачі основних типів з теми програмування з розв’язками та задачі ІІ етапу Всеукраїнської учнівської олімпіади з інформатики, що проводилась у Волинській області у 2016-2018 навчальних роках. У збірнику викладені алгоритми розв’язання задач, реалізовані мовою програмування Паскаль.
Збірник задач може бути використаний як для початкової підготовки з інформатики по програмуванню так і системної підготовки учнів до олімпіад з інформатики. У збірнику пропонуються алгоритми розв’язання типових задач основних тем програмування.
Розв’язки задач тестувалися за допомогою середовища програмування Turbo Pascal.
Збірник складається з двох розділів. Перший розділ структурований основними типами задач на використання вказівки розгалуження, циклічних алгоритмів та оператора вибору. В другому розділі місяться олімпіадні задачі ІІ туру олімпіади з інформатики у Волинській області та розв’язки до них. Може використовуватись як вчителями так і учнями.
РОЗДІЛ 1 ОСНОВНІ ТИПИ ЗАДАЧ
1.1. Лінійні програми
Задача 1.
Якщо на одну шальку терезів посадити Даринку, яка важить n кг, і Наталку, яка важить на 5 кг менше, а на іншу насипати m кг цукерок, то скільки кілограмів цукерок доведеться з’їсти дівчаткам, щоб шальки терезів врівноважились.
Введемо наступні змінні для зберігання необхідних результатів:
N - вага Даринки;
M - вага цукерок;
P - вага цукерок, що необхідно з’їсти дівчинкам.
|
Program Task_1; |
|
Uses crt; Var M, N, P : real; Begin Clrscr; Write(‘Введіть вагу Даринки ‘); Readln(N); Write(‘Введіть вагу цукерок, що лежать на терезах’); Readln(M); P := N + N – 5 – M; {N – 5 – вага Наталки} Writeln(‘Дівчаткам необхідно з’їсти ‘,P,’кг цукерок.’); Readln; {Процедура затримує зображення на |
|
екрані до натискання клавіші Enter} |
|
End. |
Задача 2.
Дано два дійсних числа a та b. Обчислити їх суму, різницю, добуток. Необхідні змінні: a, b - задані числа; Add - сума чисел; Sub - різниця чисел;
Multy - добуток чисел.
|
Program Task_2; |
|
Uses crt; Var a, b, Add, Sub, Multy : real; Begin Clrscr; Write(‘Введіть два числа ‘); Readln(a,b); Add := a + b; Sub := a – b; Multy := a*b; Writeln(‘Результати обчислень:’); Writeln(‘Сума = ‘, Add :8:2); Writeln(‘Різниця = ‘, Sub :8:2); Writeln(‘Добуток = ‘, Multy :8:2); Readkey; {Процедура затримки зображення на екрані до натискання будь-якої клавіші} End. |
Задача 3.
Визначити, яку роботу необхідно виконати, щоб підняти тіло масою m на висоту h від Землі.
Необхідні змінні:
m - маса тіла; h - висота підйому тіла; A - робота.
Математична довідка:
Робота, необхідна для підняття тіла масою m на висоту h, обчислюється за наступною формулою:
,
де g = 9,8 - таблична константа (прискорення
вільного падіння).
|
Program Task_3; |
|
Uses crt; Var m,h,A : real; Begin Clrscr; Write(‘Введіть масу тіла ‘); Readln(m); Write(‘Введіть висоту підйому тіла ‘); Readln(h); A := m*h*9.8; Writeln(‘Виконана робота дорівнює: ‘, А:8:2); Readkey; End. |
Задача 4.
Визначити, яку платню одержить на фірмі сумісник за виконану роботу, якщо йому нараховано S грн., а податок становить 20 відсотків.
Необхідні змінні:
S - сума нарахувань сумісника;
P - реальна платня, що він одержить у касі (за умовою вона становить 80% від нарахувань).
|
Program Task_4; |
|
Uses crt; Var P,S : real; Begin Clrscr; Write(‘Введіть суму нарахувань робітника ‘); Readln(S); |
|
P := S*0.8; |
|
Writeln(‘Платня сумісника становить: ‘, P:8:2); Readkey; End. |
Задача 5.
Дано гіпотенуза і один з катетів прямокутного трикутника. Знайти другий його катет і площу вписаного круга.
Необхідні змінні:
a - катет прямокутного трикутника; c - гіпотенуза прямокутного трикутника; b - довжина невідомого катета; S - площа вписаного круга.
Математична довідка:
§ b другий катет прямокутного трикутника знаходиться за теоремою Піфагора
,
звідки випливає, що катет дорівнює:
§ площа вписаного круга обчислюється за наступною формулою:
|
Program Task_5; |
|
Uses crt; Var a, b, c, S : real; Begin Clrscr; |
|
Write(‘Введіть довжину гіпотенузи ‘); |
|
Readln(с); Write(‘Введіть довжину відомого катета ‘); Readln(a); b := sqrt(sqr(c)-sqr(a)); S := Pi*(a+b-c)/2; Writeln(‘Довжина невідомого катета: ‘, b:8:2); Writeln(‘Площа вписаного кола: ‘, S:8:2); Readkey; End. |
1.2. Програми з рогалуженням Задача 1.
Чебурашка вирішив купити килими, щоб застелити кімнату, в якій він мешкав разом з Геною. Їхня прямокутна кімната виявилася розмірами a x b, де a та b - цілі числа. Коли Чебурашка запитав у магазині, які килими є у продажу, то продавець повідомив, що є квадратні килими зі стороною с, де с - ціле число.
Яку кількість килимів необхідно придбати
Чебурашці, щоб накрити максимальну площу кімнати.
Килими не можна накладати та підгинати. Визначити, яка площа кімнати буде ненакритою килимами. Передбачити ситуацію, коли розміри килиму перевищують розміри кімнати.
Очевидно, що якщо довжина сторони килима більша за будь-яку зі сторін кімнати, то застелити її цими килимами неможливо. Крім того, для знаходження кількості килимів, що вміщуються по одній зі сторін кімнати без їх підгинання, необхідно поділити націло довжину кімнати на довжину килима.
Загальна кількість килимів знаходиться за наступною формулою: K = K1 * K2, де К1 та К2 - кількості килимів, що вміщуються
вздовж двох суміжних сторін кімнати.
Площа, що незакрита килимами, визначається як різниця між площею кімнати та площею всіх куплених килимів.
|
Program Example_1; |
|
Uses crt; Var a,b,c,S:word; {a,b – розміри кімнати, с – K,K1,K2 : word; розміри килима, K1 – кількість килимів вздовж однієї стіни, К2 – кількість килимів вздовж другої стіни, К – загальна кількість |
|
килимів, S – площа кімнати, що |
|
не накрита килимами} Begin Clrscr; {Очищення екрану} Write(‘Введіть розміри кімнати: ‘); |
|
Readln(a,b); |
|
Write(‘Введіть розміри килима: ‘); Readln(с); If (c > a) or (c > b) Then writeln(‘Кімнату неможливо накрити такими килимами’) Else Begin |
|
K1:=a div c; |
|
K2:=b div c; K := K1*K2; S := a*b – K*c*c; Writeln(‘Кількість куплених килимів ‘, K); Writeln(‘Площа кімнати, що ненакрита килимами ‘, S); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 2.
Від річкового вокзалу відійшли одночасно у протилежних напрямках теплохід та турист. Теплохід рухався зі швидкістю V1 км/год, а турист по стежці вздовж річки зі швидкістю V2 км/год. Якщо через N годин турист передумає і вирішить попливти річкою назад за теплоходом зі швидкістю V3 км/год, то чи встигне він підсісти на теплохід, який має за графіком зупинку через Y годин після початку руху і стоїть на цій зупинці Z годин? Зважати на те, що всі події відбувалися протягом однієї доби.
Якщо турист на протязі N годин рухався в протилежному напрямку від теплоходу, то відстань між ними в той момент, коди турист вирішив наздогнати теплохід, була наступна:
S = (V1 + V2) * N де V1 та V2 - швидкості теплоходу та туриста відповідно.
Швидкість, з якою турист почне наздоганяти теплохід - (V3 - V1) км за годину, де V3 - швидкість, з якою турист попливе навздогін теплоходу. Час, який буде у туриста для наздоганяння, (Y - N + Z) годин, тому що зупинка у теплохода буде за розкладом через Y годин після початку руху, але N годин він вже плив, а Z годин теплохід буде стояти на цій зупинці. Тоді за цей час турист пройде відстань:
St = (V3 - V1) * (Y - N + Z)
Вочевидь, що турист встигне підсісти на теплохід тільки в тому випадку, якщо відстань St буде не менше, ніж відстань, на яку теплохід перегнав туриста.
|
Program Example_2; |
|
|
|
Uses crt; Var V1,V2,V3:real; N,Y,Z : real; Begin |
|
|
|
Clrscr; {Очищення екрану} |
|
|
|
Write(‘Введіть швидкості туриста: ‘); Readln(V1,V2); |
теплоходу |
та |
|
Write(‘Введіть час, через який турист вирішив |
||
|
підсісти на теплохід: ‘); Readln(N); Write(‘Введіть швидкість, з якою турист буде плисти за теплоходом, час, через який у теплохода зупинка, та тривалість зупинки: ‘); Readln(V3,Y,Z); If |
||
|
(V1<=0)or(V2<=0)or(V3<=0)or(N<=0)or(Y<=0)or(Z<=0) |
||
|
Then writeln(‘Помилкові вхідні дані’) Else Begin S:=(V1+V2)*N; St:=(V3-V1)*(Y-N+Z); If St>=S Then writeln(‘Турист встигне на теплохід.’) Else writeln(‘Турист не встигне на теплохід.’); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} |
||
|
End. |
||
Задача 3.
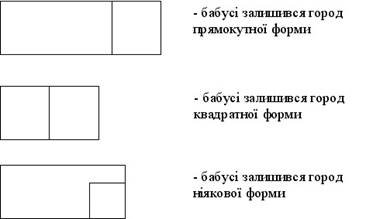
Жили собі дід і баба і був у них город прямокутної форми. Довжина городу була А м, а ширина складала В м. Якось дід посварився з бабою і вирішив поділити город порівну. Тепер у діда квадратний город зі стороною С м, відрізаний скраю, а решта дісталася бабі. Визначити, чи не залишилась баба ошуканою та якої форми дістався їй город - прямокутної чи квадратної?
Взагалі задача має дуже простий розв’язок: адже бабуся не буде ошуканою в тому випадку, якщо площа городу, що залишилася для неї, не буде меншою, ніж площа дідусевого городу, тобто
Та це тільки на перший погляд. Насправді в даній задачі може бути велика кількість винятків. Наприклад, якщо дідусь захоче відрізати собі город зі стороною, більшою, ніж сторона загального городу, то це неможливо зробити взагалі. Якщо ж він відріже, то город, що залишиться, може мати квадратну, прямокутну або ніякову форми (дивись малюнок):
|
Program Example_3; |
|
Uses crt; |
|
Var A,B,C:real; {A,B – розміри городу, С – |
|
розміри дідусевого городу} Begin Clrscr; {Очищення екрану} Write(‘Введіть розміри городу: ‘); |
|
Readln(A,B); |
|
Write(‘Введіть довжину сторони дідусевого городу: ‘); Readln(С); If (A<=0)or(B<=0)or(C<=0) Then writeln(‘Помилкові вхідні дані’) Else Begin If (C>A) or (C>B) |
|
Then writeln(‘Дідусь не зможе відрізати город |
|
такого розміру.’) else begin If A*B-sqr(C)<=sqr(C) Then writeln(‘Бабуся ошукана.’) Else writeln(‘Бабуся не ошукана.’); If (A<>C) and (B<>C) Then writeln(‘Город залишився ніякової форми’) Else If ((A=C)and(B/2=C))or((B=C)and(A/2=C)) Then writeln(‘У бабусі квадратний город.’) Else writeln(‘У бабусі прямокутний город.’); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 4.
Трьом Товстунам подали на десерт кремові тістечка. Маса одного тістечка складала Х кг, а маса Товстунів відповідно Х1 кг, Х2 кг та Х3 кг. Перший Товстун з’їв N тістечок. Кожний наступний Товстун з’їдав у два рази більше від попереднього, але при цьому він не міг з’їсти більше половини своєї власної ваги. Скільки тістечок було з’їдено Товстунами за обідом?
Зверніть увагу на те, що другий та третій Товстуни за умовою можуть з’їсти тістечок у два рази більше ніж попередній Товстун, але не можуть з’їсти більше половини своєї ваги. Тому фактично в задачі необхідно перевірити, чи не перевищує кількість тістечок, що може з’їсти кожний Товстун, дозволену масу і у відповідності до цього підрахувати кількість тістечок, що були з’їдені. Наприклад, якщо другий Товстун може з’їсти 2N тістечок, то вага цієї їжі буде 2NX кг. Але за умовою він не може з’їсти більше половини своєї ваги, тобто більше ніж X1/2 кг. Тому якщо вага тих тістечок, що Товстун може з’їсти не перевищує поріг Х1/2 кг, то ми до загальної кількості тістечок додаємо всі можливі, тобто 2N, якщо ж перевищує, то ми додаємо тільки ту кількість тістечок, що не дозволяє перевищити припустимий поріг, тобто X1/2/X (дозволена вага їжі поділити на вагу одного тістечка). Якщо в цьому випадку число вийде нецілим, то це означає, що Товстун з’їв тістечко не повністю. Щоб такого не трапилось, ми робимо відкидання дробової частини після ділення за допомогою функції trunc.
|
Program Example_4; |
|
Uses crt; Var X,X1,X2,X3:real; {Х – вага тістечка, Х1,Х2,Х3 – вага Товстунів} |
|
N,Counter : integer; {N – кількість тістечок, що |
||
|
з’їв перший Товстун; Counter – загальна кількість з’їдених тістечок} Begin Clrscr; {Очищення екрану} Write(‘Введіть вагу тістечка: ‘); Readln(Х); Write(‘Введіть вагу Товстунів (відповідно |
||
|
першого, |
||
|
другого та третього): ‘); Readln(X1, X2, X3); Write(‘Введіть кількість тістечок, що з’їв перший Товстун ‘); Readln(N); If (X<=0)or(X1<=0)or(X2<=0)or(X3<=0)or(N<=0) Then writeln(‘Помилкові вхідні дані’) Else Begin Counter:=N; {З’їв перший Товстун} If N*2*X<=X2/2 Then Counter:=Counter+2*N Else Counter:= Counter+ trunc(X2/2/X); If N*4*X<=X3/2 Then Counter:=Counter+4*N Else Counter:= Counter+ trunc(X3/2/X); Writeln(‘Кількість з’їдених тістечок становить: ‘, |
||
|
Counter); |
||
|
End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} |
||
|
End. |
||
|
|
Задача 5. |
|
Велосипедист Микола, стартувавши з точки (X0, Y0) та рухаючись по прямій A(x - X0) + B(y - Y0) + C = 0, мріє про те, як він покатає на своєму велосипеді сусідку Катрусю. Чи здійсняться мрії Миколи, якщо неподалік, у точці (P, Q), росте дерево?
В даній задачі зовсім немає проблем з вхідними даними, тому що, якщо вважати місцевість, по якій рухається Микола, координатною площиною, то його початкові координати та координати дерева можуть мати будь-яке значення. А мрія Миколчина здійснить тільки в тому випадку, коли координати дерева не співпадуть з точкою на прямій, що задає траєкторію руху Миколи, тобто при підстановці координат дерева у рівняння прямої ми не отримаємо правильну рівність.
|
Program Example_5; |
|
Uses crt; Var X0,Y0,P,Q:real; {X0,Y0 – координати точки, з якої стартував Микола; P,Q – координати дерева} A,B,C: real; {A,B,C – коефіцієнти, що задають рівняння прямої, по якій рухається Микола} |
|
Begin |
|
Clrscr; {Очищення екрану} Write(‘Введіть коефіцієнти рівняння прямої, по якій рухається Микола: ‘); |
|
Readln(A,B,C); |
|
Write(‘Введіть початкові координати хлопця: ‘); Readln(X0, Y0); Write(‘Введіть координати дерева, що знаходиться на шляху Миколки: ‘); Readln(P,Q); If A*(P-X0)+B*(Q-Y0)+C=0 Then writeln(‘Мріям Миколки не здійснитися...’) |
|
Else writeln(‘Миколки покатає Катрусю на своєму |
|
Велосипеді.’) Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 6.
Дано трикутник зі сторонами a, b, c. Визначити, який це трикутник: гострокутний, тупокутний чи прямокутний.
Для розв’язання цієї задачі необхідно нагадати дітям наступне:
1) з відрізків заданої довжини можна утворити трикутник тільки в тому випадку, якщо сума довжин будьяких двох відрізків більше довжини третього відрізка;
2) якщо з трьох відрізків можна побудувати трикутник, то він буде прямокутним тоді й тільки тоді, коли виконується теорема Піфагора, тобто, коли сума квадратів двох сторін дорівнює квадрату третьої (це співвідношення може виконуватися для однієї пари сторін);
3) для гострокутного та тупокутного трикутників теорема Піфагора перетворюється на нерівність, причому для гострокутного повинні виконуватись всі три нерівності, а для тупокутного хоча б одна (дійсно в гострокутному трикутникові всі кути менші за 90 градусів, а в прямокутному та тупокутному хоча б один дорівнює або більше 90 градусів відповідно).
Крім того, очевидно, що довжини всіх сторін не можуть бути від’ємними або нульовими.
|
Program Example_6; |
|
Uses crt; Var a,b,c:real; Begin Clrscr; {Очищення екрану} Write(‘Введіть довжини сторін: ‘); Readln(a,b,c); If (a<=0) or (b<=0) or (c<=0) Then writeln(‘Помилка вхідних даних.’) Else Begin If (a+b < c) or (a+c < b) or (c+b < a) Then writeln(‘З відрізків такої довжини утворити трикутник неможливо.’) Else Begin |
|
If (sqr(a)+sqr(b)=sqr(c)) or |
|
(sqr(a)+sqr(c)=sqr(b)) or (sqr(c)+sqr(b)=sqr(a)) then writeln(‘Трикутник прямокутний’); If (sqr(a)+sqr(b) > sqr(c)) and |
|
(sqr(a)+sqr(c) > sqr(b)) and |
|
(sqr(c)+sqr(b) > sqr(a)) then writeln(‘Трикутник гострокутний’); If (sqr(a)+sqr(b) < sqr(c)) or (sqr(a)+sqr(c) < sqr(b)) or (sqr(c)+sqr(b) < sqr(a)) then writeln(‘Трикутник тупокутний’); end End; |
|
Readkey; {Затримка зображення на екрані до |
|
натискання будь якої клавіші} End. |
Задача 7.
Дано натуральне число N (N
1000). Визначити суму першої і останньої цифр даного числа.
Для розв’язання цієї задачі ми скористаємося стандартними операціями цілочисельного ділення та остачі від ділення цілих чисел (операції div та mod).
Нагадаємо, що результатом ділення числа націло на 10 буде ефект "відкидання" молодшої цифри числа (відповідно при діленні на числа 100, 1000, 10000 тощо будемо "відкидати" дві, три або чотири цифри числа). Результатом ж операції знаходження залишку від ділення на 10 буде остання цифра числа (відповідно при знаходженні залишку від ділення на 100, 1000, 10000 будемо отримувати дві останні, три останні, чотири останні цифри числа).
Наприклад:
234 div 10 = 23
9213 div 100 = 92 52 mod 10 = 2 2845 mod 1000 = 845.
|
Program Example_7; |
|
Uses crt; Var N, First, Last : word; {N – дане число; First – перша числа числа; Last – остання цифра числа} |
|
Begin |
|
Clrscr; {Очищення екрану} Write(‘Введіть число: ‘); Readln(N); Last := N mod 10; If (N>=0) and (N<10) then First:=0; If (N>=10) and (N<100) then First:=N div 10; If (N>=100) and (N<1000) then First:=N div 100; If (N=1000) then First:=1; Writeln(‘Сума першої та останньої цифр дорівнює ‘, First+Last); Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 8.
Дано натуральне числа N (N <= 99). Визначити, чи правильно, що N^2 дорівнює кубу суми цифр цього числа.
|
Program Example_8; |
|
Uses crt; |
|
Var N, C1, C2 : word; {N – дане число; C1,C2 – перша |
|
та друга цифри числа} Begin Clrscr; {Очищення екрану} Write(‘Введіть число: ‘); Readln(N); If N>99 Then writeln(‘Помилка вхідних даних’) Else |
|
Begin |
|
C1:=N div 10; C2:=N mod 10; If sqr(N)=sqr(C1+C2)*(C1+C2) Then writeln(‘Правильно.’) Else Writeln(‘Не правильно.’); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 9.
Дано натуральне число N (N9999). Враховуючи всі чотири цифри числа, визначити, чи правильно, що воно містить дві пари цифр, що повторюються.
Для розв’язання цієї задачі теж користуємось операціями ділення націло та знаходження залишку від ділення націло для виділення цифр числа, а потім розглядаємо всі можливі варіанти співпадання пар цифр числа:
1) перша - друга та третя - четверта цифри;
2) перша - третя та друга - четверта цифри; 3) перша - четверта та друга - третя цифри.
|
Program Example_9; |
|
Uses crt; Var N,C1,C2,C3,C4:word; {N – дане число; C1,C2,C3,C4 – відповідні цифри числа} Begin Clrscr; {Очищення екрану} Write(‘Введіть число: ‘); |
|
Readln(N); |
|
If N>9999 Then writeln(‘Помилка вхідних даних’) Else Begin C1:=N div 1000; C2:=N div 100 mod 10; C3:=N div 10 mod 10; C4:=N mod 10; If ((С1=С2) and (C3=C4)) or ((С1=С3) and (C2=C4)) or ((С1=С4) and (C2=C3)) Then writeln(‘Правильно.’) Else Writeln(‘Не правильно.’); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 10.
Квадратний многочлен заданий коефіцієнтами a, b, c, де а
0. Визначити, чи корені відповідного рівняння є парними числами.
Для розв’язання цієї задачі необхідно нагадати дітям алгоритм знаходження коренів квадратного рівняння:
1) обчислити дискримінант за формулою
;
2) якщо ми отримали від’ємне число, то коренів для розв’язку квадратного рівняння з даними
коефіцієнтами a, b, c не існує;
3) якщо дискримінант не від’ємний, то корені рівняння знаходяться за наступними співвідношеннями: 
Парність коренів можна визначити, використовуючи операцію знаходження залишку від цілочисельного ділення на 2 (парне число при цьому у залишку має 0, а непарне - 1). Зверніть увагу тільки на те, що парність або непарність можна визначити тільки для цілих чисел.
|
Program Example_10; |
|
Uses crt; Var a,b,c,D,X1,X2:real; {a,b,c – коефіцієнти квадратного рівняння; D – дискримінант; X1, X2 – корені квадратного рівняння} |
|
Begin |
|
Clrscr; {Очищення екрану} Write(‘Введіть коефіцієнти квадратного рівняння a,b,c: ‘); Readln(a,b,c); |
|
If a=0 |
|
Then writeln(‘Помилка вхідних даних’) Else Begin D:=sqr(b)-4*a*c; If D<0 Then writeln(‘Рівняння не має розв”язків’) Else Begin |
|
X1:=(-b-sqrt(D))/(2*a); |
|
X2:=(-b+sqrt(D))/(2*a); Writeln(‘Корені рівняння:’); Writeln(‘X1=‘,X1:8:2); Writeln(‘X2=‘,X2:8:2); If (round(X1)<>X1)or(round(X2)<>X2) Then writeln(‘Корені рівняння не являються цілими числами.’) else if (round(X1) mod 2 =0) and (round(X2) mod 2 =0) then writeln(‘Корені рівняння парні’) else writeln(‘Корені рівняння непарні’); End; End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
Задача 11.
Дано дійсні додатні числа a, b, c, x, y. Визначити, чи пройде цеглина з ребрами a, b, c у прямокутний отвір зі сторонами x та y. Проштовхувати цеглину дозволяється лише так, щоб кожне з її ребер було паралельним чи перпендикулярним кожній зі сторін отвору.
Для розв’язання цієї задачі пропонується впорядкувати розміри отвору та розміри цеглини впорядкувати за зростанням, тобто добитися того, щоб було a b c та x y. Тоді перевірка зведеться до порівняння розмірів отвору з найменшими розмірами цеглини (адже ми можемо цеглину розвернути будь-яким боком, щоб проштовхнути її у отвір).
|
Program Example_11; |
|
Uses crt; Var a,b,c,x,y,S:real; {a,b,c – розміри цеглини; x,y – розміри отвору, S – допоміжна змінна для обміну місцями значень двох змінних} Begin Clrscr; {Очищення екрану} Write(‘Введіть розміри цеглини: ‘); Readln(a,b,c); Write(‘Введіть розміри отвору: ‘); Readln(x,y); If (a<=0) or (b<-=0) or (c<=0) or (x<=0) or (y<=0) Then writeln(‘Помилка вхідних даних.’) Else Begin |
|
If a>b |
|
Then Begin S:=a; a:=b; b:=S; End; |
|
If a>c |
|
Then Begin S:=a; a:=c; c:=S; End; If b>c Then Begin S:=b; b:=c; c:=S; |
|
End; |
|
If x>y Then Begin S:=x; x:=y; y:=S; End; If (a<=x) and (b<=y) Then writeln(‘Цеглина пройде у отвір.’) else writeln(‘Цеглина не пройде у отвір.’) End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} |
|
End. |
1.3. Цикл з параметром
Задача 1.
Ненажера Стецько пробрався перед обідом у шкільну їдальню, де вже були накриті столи, і почав швиденько з’їдати ще тепленьки булочки, що стояли на столах. З першого столу він з’їв x1 булочок, з другого – х2, і, відповідно, з останнього – xn булочок. Але за ним стежив черговий по їдальні Андрійко та ретельно все фіксував на своєму калькуляторі: до булочок, з’їдених з першого столу, додав кількість булочок, що зникли з другого столу, і т.д. Допоможіть крок за кроком відтворити інформацію, яку дістав Андрійко на своєму калькуляторі.
Очевидно, що при розв’язанні даної задачі нам на початку роботи програми відома кількість повторів, тому що ми зразу ж знаємо, скільки столів в їдальні. Крім того, зауважимо, що для зберігання кількості булочок, що знаходяться на кожному столі, не треба мати N змінних. Достатньо мати одну, назвемо її, наприклад, X, в якій тимчасово будемо зберігати відповідну кількість булочок з чергового столу. І, врешті решт, нам необхідна ще одна змінна, в якій ми будемо одержувати проміжні обчислення чергового Андрійка (наприклад,Sum).
|
Program Example_1; |
|
Uses crt; Var I,N:word; {I – параметр циклу, N – кількість столів в їдальні, тобто кількість повторень} Sum,X:word; {X – кількість булочок на черговому столі їдальні, Sum – загальна кількість булочок, що з’їв Стецько} Begin Clrscr; Sum:=0; {На початку роботи програми Стецько |
|
ще нічого не з’їв} |
|
Write(‘Введіть кількість столів в їдальні: ‘); Readln(N); For I:=1 to N do |
|
Begin |
|
Write(‘Введіть кількість булочок на черговому столі: ‘); Readln(X); Sum:=Sum+X; Writeln(‘На даний момент Стецько з”їв ‘,Sum,’ булочок.’); End; Readkey; {Затримка зображення на екрані} |
|
End. |
Задача 2.
Компанія бабусь поїхала на мотоциклах на курси комп’ютерної грамотності. Попереду на мотоциклі без глушника їхала одна бабуся, за нею - дві, потім - три і т.д. Скільки бабусь їхало на заняття, якщо приголомшені пішоходи всього нарахували N рядів? Чи змогли бабусі зайняти всі місця у класі, якщо там стояло k рядів по l комп’ютерів в кожному? Скільки вільних місць залишилося?
Зверніть увагу на те, що фактично ця задача зводиться до знаходження суми всіх натуральних чисел від 1 до N. В кінці задачі для повторення команди розгалуження учням пропонується визначити кількість зайнятих бабусями та вільних місць.
|
Program Example_2; |
|
Uses crt; Var I,N,Sum:word; {I – параметр циклу, N – кількість рядів мотоциклів, тобто кількість повторень, Sum – |
|
загальна кількість бабусь, що |
|
приїхали на курси} Place,k,l:word; {k – кількість рядів в комп’ютерному класі, l – кількість комп’ютерів в кожному ряду, Place – кількість місць, що вистачила для бабусь} Begin Clrscr; |
|
Sum:=0; |
|
Write(‘Введіть кількість рядів мотоциклів, що нарахували пішоходи: ‘); Readln(N); For I:=1 to N do Sum:=Sum+I; Writeln(‘Кількість бабусь, що приїхала на курси ‘,Sum); Writeln(‘Кількість комп”ютерів на курсах ‘,k*l); If Sum < k*l Then writeln(‘Бабусі не змогли зайняти всі місця.’) Else writeln(‘Бабусі зайняли всі місця.’); Place:=Sum – k*l; If Place>0 Then writeln(‘Бабусям не вистачило ‘,Place,’місць.’); Readkey; {Затримка зображення на екрані} End |
Задача 3.
Знайти значення
(1 + 0.1)(2 + 0.2)...(9 + 0.9)
В даному випадку, очевидною що кількість повторів буде дорівнювати 9, тобто результуюча програма буде мати вигляд:
|
Program Example_3; |
|
Uses crt; Var I:word; {I – параметр циклу} Rez:real; {Rez – результат обчислень} Begin Clrscr; |
|
Rez:=1; {Початкове значення дорівнює 1, тому |
|
що результат являється накопиченням добутку} For I:=1 to 9 do Rez:=Rez*(I+0.1*I); Writeln(‘Rez= ‘,Rez:8:2); Readkey; {Затримка зображення на екрані} End. |
Задача 4.
Дано ціле n. Визначити n!
Відомо, що n! (вимовляється, як н-факторіал) - це добуток всіх натуральних чисел від 1 до n.
|
Program Example_4; |
|
Uses crt; Var I,n:word; {I – параметр циклу} Factorial:longint; {Factorial – результат |
|
обчислень} |
|
Begin Clrscr; |
|
Factorial:=1; {Початкове значення дорівнює 1, |
|
тому що результат являється накопиченням добутку} Write(‘Введіть значення n: ‘); Readln(n); For I:=1 to n do Factorial:=Factorial*I; Writeln(‘Factorial= ‘,Factorial:8:2); Readkey; {Затримка зображення на екрані} |
|
End. |
Задача 5.
Дано ціле n.
Визначити 1*3*5*7*…*(2n+1).
Очевидно, що дана програма відрізняється від попередньої тільки тим, що необхідно знайти добуток тільки непарних натуральних чисел від 1 до n.
|
Program Example_5; |
|
Uses crt; Var I,n:word; {I – параметр циклу} Rez:longint; {Rez – результат обчислень} Begin Clrscr; Rez:=1; {Початкове значення дорівнює 1, тому що результат являється накопиченням добутку} |
|
Write(‘Введіть значення n: ‘); |
|
Readln(n); For I:=0 to n do Rez:=rez*(2*I+1); Writeln(‘Rez= ‘,Rez:8:2); Readkey; {Затримка зображення на екрані} |
End.
Задача 6.
Дано ціле n. Визначити
Sin(1)*sin(1+2)*…*sin(1+2+…+n).
Відміна даної програми від всіх попередніх полягає в тому, що в даному випадку ми маємо два накопичення: по-перше, відбувається накопичення суми, що знаходиться під знаком sin, а, по-друге, сам результат являється накопиченням добутку сінусів. Тому для зберігання цих двох накопичень необхідно мати дві змінні.
|
Program Example_6; |
|
Uses crt; Var I,n:word; {I – параметр циклу} Rez,Sum:longint; {Rez – результат обчислень, Sum – проміжне накопичення} Begin Clrscr; Rez:=1; {Початкове значення дорівнює 1, тому що результат являється накопиченням добутку} Sum:=0; {Початкове значення дорівнює 0, тому |
|
що результат являється накопиченням |
|
суми} Write(‘Введіть значення n: ‘); Readln(n); |
|
For I:=1 to n do |
|
Begin Sum:=Sum+I; {Накопичення суми} Rez:=Rez*sin(Sum); {Накопичення добутку} |
|
End; |
|
Writeln(‘Rez= ‘,Rez:8:2); Readkey; {Затримка зображення на екрані} End. |
Задача 7.
За даним натуральним значенням змінної n обчислити:
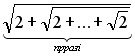
Для розв’язку цієї задачі необхідно виконати обчислення, починаючи з самого вкладеного кореня. Кожен наступний крок обчислюється наступним чином: до попереднього результату додається двійка і з отриманої суми береться квадратний корінь.
|
Program Example_7; |
|
Uses crt; Var I,n:word; {I – параметр циклу} Rez:real; {Rez – результат обчислень} Begin Clrscr; Rez:=0; {Початкове значення дорівнює 0, тому що результат являється накопиченням суми} Write(‘Введіть значення n: ‘); |
|
Readln(n); |
|
For I:=1 to n do Begin Rez:=sqrt(Rez+2); |
|
End; |
|
Writeln(‘Rez= ‘,Rez:8:2); Readkey; {Затримка зображення на екрані} End. |
Задача 8.
Дано ціле число n, яке набуває значень шкільних оцінок. Визначити відповідною кількістю звукових сигналів, яка саме оцінка була задана ("1" - один звуковий сигнал, "2" - два звукових сигнали і т.д.). Якщо ж задане число не відповідає значенню шкільної оцінки - подати довгий звуковий сигнал.
Звуковий сигнал в цій програмі можна подавати за допомогою процедур керування вбудованим динаміком Sound та nosound. Нагадуємо, що перша з них викликає звучання ноти заданої частоти (частота вказується в дужках після процедури), а друга виключає динамік. Тривалість звучання та паузи між звуками можна задавати процедурою delay, в якості параметра до якої задається змінна time (значення цієї змінної можна задати командою присвоєння або введенням з клавіатури).
|
Uses crt; |
|
Var I,n:word; {I – параметр циклу, n – оцінка учня} Time:word; Begin |
|
Clrscr; |
|
Write(‘Введіть Вашу оцінку: ‘); Readln(n); Time:=10000; {Значення цієї змінної залежить |
|
від характеристик комп’ютера, за |
|
яким працює учень, і може бути підібрана практичним шляхом} If (n<1) or (n>12) Then begin writeln(‘Ви помилились, такої оцінки не існує’); sound(200); |
|
end |
|
Else For I:=1 to n do Begin Sound(200); Delay(time); Nousound; Delay(time); End; Readkey; {Затримка зображення на екрані} End. |
1.4. Цикл з передумовою
Задача 1.
Коли Василині Премудрій виповнилося 18 років, Чахлик Невмирущий вирішив взяти її заміж. Василина запитала Чахлика, скільки у нього скринь із золотом. Чахлик сказав, що в нього зараз n скринь і щороку додається ще по m скринь. Василина пообіцяла, що вийде заміж тоді, коли у Чохлика буде k повних скринь із золотом. Скільки років буде тоді нареченій?
Program Example_1;
Uses crt;
Var m,n,k:word; {n – початкова кількість скринь з золотом, m – щорічний “прибуток” Чахлика Невмирущого, k – “потреби”
Василини Премудрої}
Sum,Years:word; {Sum – щорічне накопичення
Чахлика
Невмирущого, Years – вік Василини
Премудрої}
Begin
Clrscr;
Write(‘Введіть початкову кількість скринь з
золотом: ‘);
Readln(n);
Write(‘Введіть щорічний прибуток Чахлика: ‘);
Readln(m);
Write(‘Введіть “потреби” Василини Премудрої: ‘);
Readln(k);
Sum:=n; {Початковий “капітал” Чахлика}
Years:=18; {Початковий вік Василини}
While Sum<=k do
Begin
Sum:=Sum+m;
Years:=Years+1;
End;
Writeln(‘Василині вже виповнилося ‘,Years,’ років.’);
Readkey; {Затримка зображення на екрані} End.
Задача 2.
Капосний папуга навчився висмикувати у дідуся Василя волосся, яке ще залишилось у того на голові. Почавши з однієї волосини, він щодня збільшував порцію вдвічі. Через скільки днів дідусеві не знадобиться гребінець, якщо спочатку в нього на голові було аж N волосин.
|
Program Example_2; |
|
Uses crt; |
|
Var N,Sum:word; {N – початкова кількість волосся у |
|
дідуся Василя на голові, Sum – щоденна кількість волосся на голові} Day,K:word; {Day – кількість днів, протягом яких папуга знущався над дідусем } Begin Clrscr; Write(‘Введіть початкову кількість волосся на голові у дідуся Василя: ‘); Readln(N); Sum:=N; Day:=0; {Початок знущання} K:=1; {Початкова кількість вирваного волосся} While Sum>0 do Begin Sum:=Sum-K; K:=2*K; {Кожен день кількість вирванного волосся подвоювалась} |
|
Day:=Day+1; |
|
end; writeln(‘У дідуся волосся закінчилося на ‘,Day,’-й день.’); |
Задача 3.
Дано натуральне число n. Визначити суму цифр в числі.
Для розв’язку цієї задачі використаємо такий штучний прийом: Щоб знайти суму цифр, ми повинні "брати" цифри по одній і додавати їх одна до одної, а потім використану цифру "відкидати". На мові Паскаль це нам дозволять зробити операції ділення націло та знаходження залишку від цілочисельного ділення. Так, при діленні числа націло на 10 остання цифра числа буде "відкидатися", а при знаходженні залишку від ділення націло ми виділяємо останню цифру числа. Тобто:
123 div 10 = 12 3928 mod 10 = 8.
Процес буде повторюватись, доки від числа "нічого не залишиться", тобто, доки воно не перетвориться на нуль.
|
Program Example_3; |
|
Uses crt; Var n:longint; {N – дане число} Sum:byte; {Sum – сума цифр числа} |
|
Begin Clrscr; |
|
Sum:=0; {Сума цифр числа спочатку дорівнює 0} Write(‘Введіть ціле число: ‘); |
|
Readln(N); |
|
N:=abs(N); While N>0 do Begin Sum:=Sum+N mod 10; {Знаходження суми цифр} N:=N div 10; {“Відкидання” останньої цифри числа } End; Writeln(‘Sum= ‘,Sum); |
|
Readkey; {Затримка зображення на екрані} |
|
End. |
Задача 4.
Дано дійсне число а. Знайти таке найменше n,
що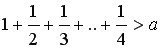 
.
Очевидно, що в даному випадку невідомо, на якому кроці ми досягнемо бажаного результату, тому необхідно використати цикл з передумовою для перевірки досягнення бажаного результату.
Зверніть увагу, що при деяких значеннях а дана сума ніколи не досягне заданого значення. Наприклад, при від’ємному або дуже великому значенні змінної а.
|
Program Example_4; |
|
|
Uses crt; |
|
|
Var n:word; {n – шукане число} |
|
|
Rez,a:real; {Rez – результат обчислень, а – граничне значення} Begin |
|
|
Clrscr; |
|
|
n:=1; {Початкове значення n - 1} Write(‘Введіть значення a: ‘); Readln(a); Rez:=0; {Початкове значення суми} While Rez<=a do Begin Rez:=Rez+1/n; n:=n+1; |
|
|
end; |
|
|
Writeln(‘n= ‘,n); Readkey; {Затримка зображення на екрані} End. |
|
|
|
|
Задача 5.
Знайти найбільше додатне число n, для якого виконується умова: 
.
Очевидно, що починаючи зі значення n=1 і збільшуючи його на одиницю після кожного кроку, ми знайдемо таке ціле число, при якому вказана нерівність буде вірною.
|
Program Example_5; |
|
|
Uses crt; Var n:word; {n – шукане число} Begin Clrscr; |
|
|
n:=1; |
|
|
While –4*n+841*sqrt(n)+3>=0 do n:=n+1; Writeln(‘n= ‘,n); Readkey; {Затримка зображення на екрані} |
|
|
End. |
|
|
|
|
Задача 6.
Дано ціле число m>1. Знайти найбільше число k, при якому виконується умова 4k < m.
Задача 7.
Під час обчислення результатів деяких експериментів виникає необхідність отримання результату із заданою похибкою. Нехай результатом є нескінченна сума, що задається певною формулою, і відома похибка e (e > 0) для знаходження наближеного значення результату. Будемо вважати, що необхідна точність досягнута, коли додавання наступного доданку змінює
суму 
на величину, меншу за e. Обчислити:
|
Program Example_7; |
|
Uses crt; Var i:word; Rez,Epsilon:real; {Rez – результат обчислень, |
|
Epsilon - похибка} |
|
Begin Clrscr; Rez:=0; {Початкове значення дорівнює 0, тому що результат являється накопиченням суми} Write(‘Введіть значення похибки (Е>0): ‘); Readln(Epsilon); i:=1; While 1/sqr(i)>Epsilon do Begin Rez:=Rez+1/sqr(i) i:=i+1; End; Writeln(‘Rez= ‘,Rez:8:2); Readkey; {Затримка зображення на екрані} End. |
Задача 8.
Обчислити значення числа p, використовуючи формулу
Визначити, яка кількість доданків дає значення числа p з точністю до 3 знаків.
Для організації циклу з передумовою в цій задачі необхідно мати еталон числа p для порівняння з нескінченною сумою. Візьмемо в якості цього еталону значення вбудованої функції Pi. Крім того, за умовою задачі нам необхідно отримати результат з точністю до третьої цифри після коми.
Пропоную для цього стандартне число Pi і отриману нескінченну суму помножити на число 1000 та округлити результат за допомогою функції round (отриману суму, крім того, необхідно ще помножити на 4, так як сама сума являється чвертю числа p).
Зверніть увагу також на те, що в нескінченній сумі доданки, що стоять на парних місцях додаються зі знаком "+", а доданки на непарних місцях - віднімаються від суми. Тобто в залежності від номера доданку (парний чи ні) ми організовуємо знакочергування у нескінченній сумі.
|
Program Example_8; |
|
Uses crt; Var i,n:word; {і – параметр циклу, n – кількість доданків} Rez_Pi:real; {Rez_Pi – обчислене значення числа |
|
Pi} |
|
Begin Clrscr; Rez_Pi:=0; i:=1; {i – значення знаменника першого доданка} |
46
|
n:=0; {n – доданків ще нема} |
|
|
while round(pi*1000)=round(Rez_Pi*4000) do Begin If n mod 2 = 0 Then Rez_Pi:=Rez_Pi+1/i Else Rez_Pi:=Rez_Pi-1/i; i:=i+2; n:=n+1; End; |
|
|
Writeln(‘Кількість необхідних доданків - ‘,n); |
|
|
Writeln(‘Порівняйте значення Pi: ‘); Writeln(‘Результат обчислень програми: ‘,Rez_Pi:8:3); Writeln(‘Вбудована функція: ‘,Pi:8:3); Readkey; {Затримка зображення на екрані} End. |
|
|
|
|
1.5. Цикл з післяумовою
Задача 1.
На дверях ліфта висіло загрозливе попередження про те, що двері зачиняються самі в той самий момент, коли зайвий за вагою пасажир переступить поріг ліфта. Котрий пасажир постраждає, якщо ліфт витримує вагу не більше S кг, а вага пасажирів, що стоять у черзі до ліфта, дорівнює відповідно a1, a2, a3, … an?
В цій задачі зручніше використовувати цикл с післяумовою, тому що спочатку необхідно дати можливість "ввійти" пасажиру в ліфт, а потім перевіряти, чи витримає його ліфт. Умовою виходу з циклу буде перевищення сумарної ваги пасажирів, що увійшли в ліфт, деякого заданого критичного значення. Для зберігання ваги чергового пасажиру в цій задачі ми будемо використовувати одну й ту саму змінну (А), так як після перевірки вага пасажира нас вже не цікавить.
Program Example_1;
Uses crt;
Var N:word; {I – номер пасажира, що увійшов у ліфт}
Sum,A,S:real; {Sum – сумарна вага пасажирів, що
знаходяться в ліфті, A – вага чергового пасажира, що увійшов до ліфта, S – критична вага, що може
бути піднята ліфтом}
Begin
Clrscr;
Sum:=0; {На початку роботи програми в ліфті
N:=0; немає пасажирів}
Write(‘Введіть критичну вагу, що піднімає ліфт:
‘);
Readln(S);
Repeat
Write(‘Введіть вагу чергового пасажира: ‘);
Readln(А);
Sum:=Sum+А;
N:=N+1;
Until Sum>S;
Writeln(‘Постраждає ‘,N,’-й пасажир.’); Readkey; {Затримка зображення на екрані} End.
Задача 2.
Капосний папуга навчився висмикувати у дідусі Василя волосся, яке ще залишилося у того на голові. Почавши з однієї волосини, він щодня збільшував порцію вдвічі. Через скільки днів дідусеві не знадобиться гребінець, якщо спочатку в нього на голові було аж Nволосин?
Аналогічно попередній задачі, аналізувати наявність волосся на голові необхідно після того, як папуга вже висмикнув чергову порцію волосся. А "знущання" над дідусем скінчиться тоді, коли гребінець йому стане непотрібним, тобто кількість волосся на голові стане дорівнювати нулю.
Зверніть увагу, що в цій задачі змінна S використовується для підрахунку чергової порції волосся, що підлягає висмикуванню капосним папугою.
|
Program Example_2; |
|
|
Uses crt; Var S,N,Sum:longint; {S – кількість волосся, що буде висмикнуто, Sum – кількість волосся, що залишилося в дідуся на голові, N – початкова кількість волосся} Day:word; {Day – номер дня, який папуга знущається над дідусем} |
|
|
Begin |
|
|
Clrscr; Write(‘Введіть початкову кількість волосся в дідуся на голові: ‘); Readln(N); |
|
|
If N=0 |
|
|
Then writeln(‘Дідусь вже лисий, папузі нічого робити!’) Else begin Day:=0; Sum:=N; S:=1; {Початкова кількість волосся, що буде висмикнутою капосним папугою} |
|
|
Repeat |
|
|
Sum:=Sum-S; {Зменшення дідусевого волосся} S:=S*2; Day:=Day+1; {Підрахунок номера дня} Until Sum<=0; Writeln(‘Папуга знущався над дідусем ‘,Day,’ днів.’); End; Readkey; {Затримка зображення на екрані} End. |
|
|
|
|
Задача 3.
Дано натуральне число n. Визначити кількість цифр у цьому числі.
Для розв’язання цієї задачі можна використати як цикл з передумовою, так і цикл с післяумовою. Однак, на наш погляд, другий варіант кращий, тому що навіть число "0" має у своєму складі одну цифру, а цикл з передумовою цей випадок пропустить. Справа в тому, що умовою виходу з циклу і в тому, і в другому випадку буде "зникнення" числа, тобто перетворення його на нуль після відкидання чергової цифри, а, якщо число з самого початку дорівнює "0", то цикл з передумовою не виконається ні разу, а цикл с післяумовою виконається обов’язково і підрахує одну цифру. Програма для розв’язання цієї задачі має наступний вигляд:
Program Example_3;
Uses crt;
Var N:longint; {N – задане число}
Count:byte; {Count – кількість цифр в числі}
Begin
Clrscr;
Write(‘Введіть натуральне число: ‘);
Readln(N);
N:=abs(N); {Знаходження модуля числа для позбавлення від помилкового введення ненатурального числа}
Count:=0; {Початкове значення кількості цифр}
Repeat
Count:=Count+1;
N:=N div 10; {“Відкидання” останньої цифри числа після підрахунку}
Until N = 0;
Writeln(‘Кількість цифр в числі = ‘,Count); Readkey; {Затримка зображення на екрані} End.
Задача 4.
Під час обчислення результатів деяких експериментів виникає необхідність отримання результату із заданою похибкою. Нехай результатом є нескінченна сума, що задається певною формулою, і відома похибка e (e > 0) для знаходження наближеного значення результату. Будемо вважати, що необхідна точність досягнута, коли додавання наступного доданку змінює суму на величину, меншу за e. Обчислити:
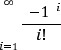
В даній задачі ми візьмемо додаткову змінну (S), яка буде зберігати наступний доданок до нескінченої суми. Умовою виходу з циклу буде зменшення величини цього доданку до значення e по модулю. Зверніть увагу ще на те, що вираз 
фактично призводить до знакочергування в нескінченній сумі, тому, щоб не знаходити степінь числа -1 можна враховувати номер доданку і, якщо він буде парним, віднімати черговий доданок, якщо ні - додавати.
|
Program Example_4; |
|
|
Uses crt; Var i:word; {i – номер доданка} S,Sum:real; {S – черговий доданок, Sum – нескінченна сума} Epsilon:real; {Epsilon – задана похибка обчислень} Begin Clrscr; |
|
|
Write(‘Введіть значення похибки: ‘); |
|
|
Readln(Epsilon); Sum:=0; {Початкове значення дорівнює 0 для накопичення суми} |
|
|
S:=1; {Перший доданок нескінченної суми за |
|
|
умовою дорівнює “1”} i:=1; repeat if i mod 2 =0 then Sum:=Sum + 1/S else Sum:=Sum - 1/S; i:=i+1; S:=S*i; |
|
|
until 1/S<=Epsilon; |
|
|
Writeln(‘Результат обчислень = ‘,Sum:8:2); Readkey; {Затримка зображення на екрані} End. |
|
|
|
Задача 5. |
На скільки років необхідно покласти в банк суму Х грошових одиниць, щоб одержати суму N грошових одиниць (N > X), якщо банк нараховує 200% річних?
Очевидно, що умовою виходу з цього циклу буде отримання заданої суми грошей. Якщо за умовою задачі N > X, то кожну перевірку ми будемо виконувати після того, як до вкладеної суми додамо щорічний банківський процент.
|
Program Example_5; |
|
|
Uses crt; Var X,N:real; {X – початковий вклад, N – бажана сума} |
|
|
Rez:real; {Rez – результуюча сума на |
|
|
рахунку} Years:longint; {Years – термін, протягом якого сума лежала в банку} Begin |
|
|
Clrscr; |
|
|
Write(‘Введіть початкову суму вкладу: ‘); Readln(Х); Write(‘Введіть бажану суму вкладу: ‘); Readln(N); If N<=X Then writeln(‘Ви вже маєте бажану суму!’) Else Begin |
|
|
Rez:=X; |
|
|
Years:=0; Repeat Rez:=3*Rez; {200% річних збільшують за рік вклад втричі} Years:=Years+1; Until Rez>=N; Writeln(‘Ви отримаєте бажану суму через ‘,years,’ років.’); End; Readkey; {Затримка зображення на екрані} End. |
|
|
|
|
Задача 6.
Скласти програму, яка б допомогла працівникам ДАІ визначати кількість порушників перевищення швидкості на трасі, якщо відомо, що на даному проміжку траси встановлено обмеження на швидкість Vmax, а прилад фіксує швидкість автомобілів V1, V2, …, Vn.
В даній задачі ніяким чином не обумовлена умова виходу з циклу, тому є пропозиція: процес підрахування порушників необхідно закінчити тоді, коли чергове введене число буде недодатнім (дійсно, з від’ємною або нульовою швидкістю автомобіль рухатися не може). Для тимчасового зберігання швидкості чергового водія ми будемо знову використовувати одну змінну.
Program Example_6;
Uses crt;
Var V,Vmax:real; {V – швидкість чергового водія, Vmax – максимально дозволена швидкість}
Count:longint;{Count – кількість порушників}
Begin
Clrscr;
Count:=0; {На початку роботи порушники
відсутні}
Write(‘Введіть значення максимально дозволеної швидкості: ‘);
Readln(Vmax);
Vmax:=abs(Vmax); {Знаходження модуля для виключення помилки введення від’ємної максимальної
швидкості}
Repeat
Write(‘Введіть значення швидкості чергового водія: ‘);
Readln(V);
If V>Vmax then Count:=Count+1;
Until V<=0;
Writeln(‘Кількість порушників ‘,Count); Readkey; {Затримка зображення на екрані} End.
Задача 7.
Дано натуральні числа n i a1, a2, …, an. Визначити кількість членів ak послідовності a1, a2, …, an, що кратні числу 3 і не кратні числу 7.
Взагалі цю задачу можна розв’язувати з використанням циклу з параметром, так як на початку роботи програми задається число n, що вказує кількість чисел, що вводяться. Але можна цю змінну використати для організації циклу з післяумовою і отримати інший розв’язок задачі, що вам і пропонується:
|
Program Example_7; |
|
Uses crt; Var n:word; {n – кількість чисел, що вводяться} a,count:word; {a – змінна, що зберігає чергове введене число; count – кількість чисел, що задовольняє заданій умові} Begin Clrscr; count:=0; {На початку роботи кількість знайдених чисел дорівнює 0} Write(‘Введіть кількість чисел, що будуть вводитись: ‘); Readln(n); Repeat Write(‘Введіть чергове число: ‘); |
|
Readln(a); |
|
If (a mod 3 = 0) and (a mod 7 <> 0) Then count:=count+1; n:=n-1; Until n<0; |
Задача 8.
Дано натуральне число n і дійсні числа a1, a2, …, an (a10). Відомо, що в заданій послідовності є хоча б одне нульове значення. Розглядаючи члени послідовності, що розташовані до першого нульового члена, визначити середнє арифметичне членів.
Для розв’язку цієї задачі значення n, являється зайвим, якщо серед членів послідовності буде хоча б один нульовий елемент, тому ми враховувати цю змінну не будемо (хоча дітям можна пояснити, що у випадку відсутності нульового члена послідовності змінна n може використовуватись як додаткова для виходу з циклу, щоб виключити зациклення програми).
Зверніть увагу на те, що так як ми не знаємо, коли зустрінеться нульовий елемент, в програмі знаходиться сума всіх чисел послідовності (змінна Sum) та кількість введених чисел ( змінна сount), а після виходу з циклу вже знаходиться безпосередньо середнє арифметичне членів послідовності, як результат ділення суми на кількість чисел, зменшену на одиницю. Зменшення на одиницю відбувається тому, що фактично в тілі циклу буде підраховано один зайвий нульовий елемент (останній)
|
Program Example_8; |
|
|
Uses crt; Var count:word; {count – кількість членів |
|
|
послідовності до першого нульового |
|
|
елемента} a,Sum:real; {a – черговий член послідовності, Sum – сума членів послідовності до першого “0”} SA:real; {SA – середнє арифметичне} Begin Clrscr; Sum:=0; |
|
|
count:=0; {Початкові значення дорівнюють “0”} |
|
|
repeat write(‘Введіть черговий член послідовності: ‘); readln(a); Sum:=Sum+a; count:=count+1; until a=0; SA:=Sum/(count-1); Writeln(‘Середнє арифметичне = ‘,SA:8:2); Readkey; {Затримка зображення на екрані} End. |
|
|
|
|
1.6. Вказівка вибору
Задача 1.
Розробити діалогову програму, яка запитує вік користувача і визначає, до якої вікової категорії він належить:
1) від 1 до 10 років - дитина;
2) від 11 до 15 років - підліток;
3) від16 до 20 років - юнак (юнка);
4) від 21 до 30 років - молода людина;
5)після 31 року - доросла людина.
Особливих пояснень ця задача не потребує, адже її можна розв’язати і за допомогою команди розгалуження. Однак зробимо її за допомогою команди вибору, причому, щоб скористатися гілкою Else, будемо вважати, що людина може мати вік не більше 150 років (навіть за всіма відомими рекордами, людина не може жити більше 150 років). Якщо ж користувач введе число, що не входить в дозволений діапазон, будемо вважати, що він пожартував. Program Example_1;
|
Uses crt; |
|
|
Var Years:byte; {Years – вік користувача} Begin Clrscr; {Очищення екрану} Write(‘Введіть Ваш вік: ‘); Readln(Years); Write(‘Ви ‘); Case Years of 0..10: Writeln(‘- дитина.’); 11..15: Writeln(‘- підліток.’); 16..20: Writeln(‘- юнак (юнка).’); 21..30: Writeln(‘- молода людина.’); 31..150: Writeln(‘- доросла людина.’) Else writeln(‘, мабуть, пожартували? Людина стільки не живе!’); End; |
|
|
Readkey; {Затримка зображення на екрані до |
|
|
натискання будь якої клавіші} End. |
|
|
|
|
Задача 2.
Розробити програму видачі номеру кварталу, до якого відноситься місяць, заданий числом від 1 до 12. Usescrt;
Var Month:byte; {Month – номер місяця}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть номер місяця: ‘);
Readln(Month);
Case Month of
1..3: Writeln(‘Перший квартал.’);
4..6: Writeln(‘Другий квартал.’);
7..9: Writeln(‘Третій квартал.’);
10..12: Writeln(‘Четвертий квартал.’);
Else writeln(‘Помилка вхідних даних.’);
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші} End.
Задача 3.
Розробити програму виведення інформації про день тижня, - вихідний він чи робочий, якщо задано його номер від 1 до 7 (1 - понеділок).
|
Program Example_3; |
|
|
Uses crt; |
|
|
Var Day:byte; {Day – номер дня тижня} |
|
|
Begin Clrscr; {Очищення екрану} Write(‘Введіть номер дня тижня: ‘); |
|
|
Readln(Day); |
|
|
Case Day of 1..5: Write(‘Це робочий день ‘); 6,7: Write(‘Це вихідний день ‘); Else write(‘Це не день ‘); End; Writeln(‘тижня.’); Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} |
|
|
End. |
|
|
|
|
Задача 4.
Дано ціле число N (1 N 3) та дійсне число X. За даним значенням змінної N, яка є номером функції, визначити:
1) sin X;
2) cos X; 3) tg X.
|
Program Example_4; |
|
|
Uses crt; Var N:byte; {N – номер функції, що обчислюється} X,Y:real; {X – значення змінної, Y – значення функції} Begin Clrscr; {Очищення екрану} Write(‘Введіть значення Х: ‘); |
|
|
Readln(Х); Write(‘Введіть номер функції, що обчислюється: |
|
|
‘); Writeln(‘1 - sin’); Writeln(‘2 - cos’); |
|
|
Writeln(‘3 - tg’); |
|
|
Readln(N); Writeln(‘Результат обчислень:’) Case N of 1: begin Y:=sin(X); writeln(‘sin(x)=‘,Y:8:2); end; 2: begin Y:=cos(X); writeln(‘cos(x)=‘,Y:8:2); end; 3: begin Y:=sin(X)/cos(X); writeln(‘tg(x)=‘,Y:8:2); end; Else writeln(‘Помилка вхідних даних.’); |
|
|
End; |
|
|
Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
|
|
|
|
Задача 5.
Розробити алгоритм-"лотерею", який, використовуючи генератор випадкових чисел, визначатиме призи:
1) комп’ютер;
2) принтер;
3) сканер; 4) компакт-диск; 5) набір дискет.
Якщо ми хочемо зробити безпрограшну лотерею, необхідно примусити генератор випадкових чисел генерувати числа в діапазоні від 1 до 5. Для цього можна скористатися наступним виразом:
Random(4) + 1.
Нагадуємо, що генератор генерує цілі числа в діапазоні від 0 до числа, що вказано в дужках після слова random, але додаванням до цього виразу одиниці ми позбавимось числа 0. Таким чином програма для розв’язання цієї задачі має наступний вигляд:
Program Example_5;
Uses crt;
Var N:byte; {N – генерований номер лотереї}
Begin
Clrscr; {Очищення екрану}
Randomize; {Процедура, що примушує програму генерувати при кожному новому
запуску програми нові числа}
N:=random(4)+1;
Write(‘Вітаємо! Ви виграли ‘)
Case N of
1: writeln(‘комп’ютер!!!’);
2: writeln(‘принтер!!!’);
3: writeln(‘сканер!!!’);
4: writeln(‘компакт-диск!!!’);
5: writeln(‘набір дискет!!!’);
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші} End.
Задача 6.
Дано натуральне число N (N 100), яке позначає вік людини. Додати до цього числа відповідно слова: "рік", "роки", "років", наприклад: 1 рік, 12 років, але 43 роки.
Очевидно, що для того, щоб правильно дописати відповідне слово, необхідно виділити останню цифру числа, що позначає вік людини. Тоді, якщо це цифра "1", то дописується слово "рік", якщо цифри "2", "3" або "4" - дописується слово "роки", а в усіх останніх випадках - дописується слово "років". Виключенням являється діапазон між 10 та 20 роками: в цих випадках завжди пишеться слово "років".
|
Program Example_6; |
|
Uses crt; |
|
Var Years:byte; {Years – вік людини} |
|
Begin Clrscr; {Очищення екрану} Write(‘Введіть Ваш вік: ‘); Readln(Years); Write(‘Вам ‘,Years); If (Years>=10) and (Years<=20) Then writeln(‘років’) Else Case Years mod 10 of 1: writeln(‘рік.’); 2..4: writeln(‘роки.’); 0,5..9: writeln(‘років.’); End; Readkey; {Затримка зображення на екрані до натискання будь якої клавіші} End. |
РОЗДІЛ 2
ЗАДАЧІ II ЕТАПУ
ВСЕУКРАЇНСЬКОЇ УЧНІВСЬКОЇ ОЛІМПІАДИ З
ІНФОРМАТИКИ
2.1. 2016-2017 рік
Задача 1. Годинник
|
Ім’я вхідного файлу: |
clock.dat |
|
Ім’я вихідного файлу: |
clock.sol |
|
Максимальний час роботи на одному тесті: |
1 секунда |
Старовинний годинник б’є щопівгодини. Причому на початку кожної години він б’є стільки раз, скільки годин (по 1 разу – в час ночі і в час дня, по 2 рази – в дві години ночі та в дві години дня і так далі, опівночі і опівдні вони б’ють, відповідно, по 12 разів). І ще 1 раз вони ‘‘ють в середині кожної години.
Даний проміжок часу (відомо, що пройшло строго менше 24 годин). Напишіть програму, що визначає, скільки ударів зробив годинник за цей час.
Формат вхідних даних
У першому рядку записаний початковий момент часу, в другому рядку — кінцевий. Моменти часу задаються двома цілими числами, що розділяються пропуском. Перше число задає години (від 0 до 23), друге - хвилини (від 1 до 59, при цьому воно не дорівнює 30).
Формат вихідних даних
У вихідний файл виведіть одне число — скільки ударів зробив годинник за цей відрізок часу. Приклади
|
clock.dat |
clock.sol |
|
5 20 10 25 |
45 |
|
10 25 5 20 |
135 |
|
5 2 5 21 |
0 |
Розв’язок перший: моделювання.
“Крутитимемо” стрілки годинника, кожну хвилину оцінюючи ситуацію і рахуючи удари. Цей алгоритм можна реалізувати, наприклад, так.
while (h1 <> h2) or (m1 <> m2) do begin
inc(m1); {додаємо одну хвилину}
if m1 = 60 then begin
inc(h1); h1 := h1 mod 24; m1 := 0; if h1 mod 12 = 0 then
inc(res, 12)
else
inc(res, h1 mod 12);
end else if m1 = 30 then inc(a); end;
(тут h1:m1 – початковий час, h2:m2 – кінцевий час, res – кількість ударів).
Розв’язок другий: підрахунок ударів.
Хай початковий час менше кінцевого. Тоді можна підрахувати кількість ударів таким чином. Загальна кількість ударів складається з
- “годинних” ударів в моменти часу (h1+1):00,
(h1+2):00, ., h2:00;
- “півгодинних” ударів в моменти часу
(h1+1):30, (h1+2):30, ., h2:30;
- “півгодинного” удару у момент часу h1:30, якщо m1<30;
- “півгодинного” удару у момент часу h2:30, якщо m2>30.
Тепер відмітимо, що за добу годинник б’є 180 разів. Тому у разі, коли кінцевий час менше початкового, можна поміняти їх місцями, обчислити кількість ударів за приведеною вище схемою і відняти отримане число з 180.
Розв’язок третый: явна формула. Позначимо через
U(t1,t2) кількість ударів в проміжок часу [t1,t2]. Тоді
U(t ,0)-U(t ,0),2 1 если t2
U(t ,t )=1 2
180+U(t ,0)-U(t ,0),2 1 если t
Для величини U(t,0) теж можна вивести явну формулу. Наприклад, таку:
U(h:m,0)= (h DIV 12) * 78 + {Кількість
“годинних” ударів за повних 12 годин }
+ (h MOD 12) * ((h MOD 12) + 1) DIV 2
{кількість “годинних” ударів
за останній час }
+ h {кількість “півгодинних”
ударів}
+ ord (m > 30) {ще один “півгодинний” удар
якщо m>30 }
Задача 2. Двоякі числа
|
Ім’я вхідного файлу: |
|
number.dat |
|
Ім’я вихідного файлу: |
|
number.sol |
|
Максимальний час роботи одному тесті: |
на |
2 секунди |
Натуральне число називається двояким, якщо в його десятковому записі зустрічається не більше двох різних цифр. Наприклад, числа 3, 23, 33, 100, 12121 — двоякі, а числа 123 і 9980 — ні.
Для заданого натурального числа N потрібно знайти найближче до нього двояке число (якщо таких чисел два — будь-яке з них).
Формат вхідних даних
У вхідному файлі записано одне натуральне число N, що не перевершує 30000.
Формат вихідних даних
У вихідний файл потрібно видати одне найближче двояке до N.
Приклади
|
number.dat |
number.sol |
|
123 |
122 |
|
2012 |
2020 |
|
11111 |
11111 |
Розв’язок
Обмеження на вхідні дані дозволяє перебрати всі
числа, виділити серед них всі двоякі і вибрати з цих чисел найближче до N. Достатньо перебрати числа від 1 до 300000, оскільки задане число лежить в цьому діапазоні, а 1 і 300000 самі є двоякими числами. Можна і розв’язати шляхо пошук від даного числа вліво та вправо і перевіркою на двоякість розбиттям на цифри і підрахунком кількості цифр, або занесенням в множину.
var n,i:longint;
function dv (i : longint) : boolean; var
s,first,second: integer; begin
first:=-1;second:=-1; dv:=true; while i>0 do begin s := i mod 10; i:= i div 10; if (s<>first) AND (s<>second) then
if first=-1 then first:=s
else
if second=-1 then second:=s
else dv:=false;
end; end; begin
assign(INPUT,’number.dat’); Reset(INPUT);
assign(OUTPUT,’number.sol’);
Rewrite(OUTPUT);
read(n);
i:=0;
while NOT (dv(n-i) or dv(n+i)) do
INC(i);
if(dv(n-i)) then writeln (n-i)
else writeln (n+i); close(input); close(output); end.
Задача 3. Станції
|
Ім’я вхідного файлу:
|
|
|
station.dat |
|
Ім’я вихідного файлу: |
|
|
station.sol |
|
Максимальний час одному тесті: |
роботи |
на |
3 секунди |
На деякій залізничній вітці розташовано N станцій, які послідовно пронумеровані числами від 1 до N. Відомі відстані між деякими станціями. Потрібно точно обчислити довжини всіх перегонів між сусідніми станціями або вказати, що це зробити неможливо (тобто приведена інформація є суперечливою або її недостатньо).
Формат вхідних даних
У вхідному файлі записані спочатку числа N — кількість станцій (2<=N<=100) і E — кількість пар станцій, відстані між якими задані (0<=E<=10000). Далі йде E трійок чисел, перші два числа кожної трійки задають номери станцій (це числа з діапазону від 1 до N), а третє — відстань між цими станціями (всі ці відстані задані точно і виражаються дійсними додатними числами не більше ніж з 3-ма знаками після десяткової крапки).
Формат вихідних даних
У разі, коли відновити довжини перегонів можна однозначно, у вихідний файл виведіть спочатку число 1, а потім N–1 дійсних чисел. Перше з цих чисел повинно відповідати відстані від 1-ої станції до 2-ої, друге — від 2ої до 3-ої, і так далі. Всі числа мають бути виведені з точністю до 3-х знаків після десяткової крапки.
Якщо приведена інформація про відстані між станціями є суперечливою або не дозволяє однозначно точно відновити довжини перегонів, виведіть у вихідний файл одне число 2.
Приклади
|
station.dat |
station.sol |
|
3 2 1 2 1.250 3 1 3 |
1 1.250 1.750 |
|
4 4 1 2 1.250 1 3 1.255 2 4 0.010 1 1 0.000 |
1 1.250 0.005 0.005 |
|
5 6 1 4 3.000 3 1 2.000 2 4 2.000 1 2 1.000 4 2 2.000 3 5 1.000 |
1 1.000 1.000 1.000 0.000 |
|
3 1 1 1 1 |
2 |
|
3 3 1 2 1.250 1 3 1.300 2 3 1.000 |
2 |
|
3 2 1 2 1.000 1 3 0.005 |
2 |
|
4 2 1 2 1.250 1 4 1.251 |
2 |
Розв’язок
Const MaxN = 100; eps = 1e-4; Var
N, E: Integer;
Ras: Array [1..MaxN, 1..MaxN] Of Real;
Was: Array [1..MaxN] Of Boolean;
Rs: Real;
Res,x,y,i,j: Integer;
Function Eq(a,b: Real): Boolean;
Begin
Eq := Abs(a-b) < eps;
End;
Function Less(a,b: Real): Boolean;
Begin
Less := (a-b) <= -eps;
End;
Function Sign(x: Integer): Integer;
Begin
If x > 0 Then Sign := 1 Else
If x = 0 Then Sign := 0 Else Sign := -1;
End;
{at first x<y}
Function GetRas(x,y: Integer): Real;
Var i: Integer; Rs: Real;
Begin
Rs := -1;
Was[x] := True;
If Not Eq(Ras[x,y], -1) Then GetRas := sign(y-
x)*Ras[x,y] Else Begin
i := 1;
While (i <= N) And Eq(Rs, -1) Do
Begin
If Not Was[i] And Not Eq(Ras[x,i], -1) Then
Rs := GetRas(i,y);
inc(i);
End;
If (i <= N) Then
Begin
dec(i);
Ras[x,y] := sign(i-x)*Ras[x,i] + Rs;
GetRas := Ras[x,y];
Ras[x,y] := Abs(Ras[x,y]);
End
Else GetRas := -1;
End;
End;
2.2. Завдання II етапу 2011-2012 рік
Задача 1. «Прямокутники»
|
Ім’я файлу програми: |
RECTANGLE.* |
|
Ім’я вхідного файлу: |
RECTANGLE.DA T |
|
Ім’я вихідного файлу: |
RECTANGLE.SOL |
|
Максимальний час роботи на одному тесті: |
1 секунда |
Шоколадну плитку спочатку розламали N разів, потім кожну утворену частину розділили M разів. Визначити загальну кількість утворених прямокутників.
Вхідні дані. Вхідний текстовий файл містить єдиний рядок з двох чисел розділених пропуском
(0<=N,M<=2147483647).
Вихідні дані. Вихідний текстовий файл містить єдине ціле число – кількість прямокутників. Приклад файлів
|
RECTANGLE.DAT |
RECTANGLE.SOL |
|
1 1 |
4 |
Розв’язок
Кількість прямокутників при першому поділі рівна N+1. При наступних поділах кількість стане (N+1)*(M+1). Програма
var r,n,m:int64; begin
assign(input,’rectangle.dat’);
reset(input); readln(n,m); close(input);
assign(output,’rectangle.sol’); rewrite(output); r:=(n+1)*(m+1); writeln(r); close(output); end.
Задача 2. «Квадрат»
|
Ім’я файлу програми: |
SQUARE.* |
|
Ім’я вхідного файлу: |
SQUARE.DAT |
|
Ім’я вихідного файлу: |
SQUARE.SOL |
|
Максимальний час роботи на одному тесті: |
1 секунда |
Дано цілі числа N та M, які задають розмір шоколадної плитки. Визначити найменшу кількість частинок квадратної форми, на яку можна поділити плитку. Вхідні дані. Вхідний текстовий файл містить єдиний рядок з двох чисел розділених пропуском (0<N, M<=264).
Вихідні дані. Вихідний текстовий файл містить єдине ціле число – кількість квадратів. Приклад файлів
|
SQUARE.DAT |
SQUARE.SOL |
|
2 4 |
2 |
Розв’язок
Кількість квадратів шляхом відкидання квадратів з стороною рівною меншій стороні прямокутника. Для прискорення роботи програми відкидання здійснювати не операцією віднімання, а операціями цілочисельного ділення і остачі від ділення. Передбачити використання 64 бітного типу даних. Програма
var rez,n,m:int64;
begin
assign(input,’SQUARE.dat’);
reset(input); readln(n,m); close(input); rez:=0;
while (n>0) and (m>0) do begin if n>m then begin rez:=rez+n div m; n:=n mod m;
end else begin rez:=rez+m div n;
m:=m mod n; end; end;
assign(output,’SQUARE.sol’); rewrite(output); writeln(rez); close(output); end.
Завдання 3. «Ламана»
|
Ім’я файлу програми: |
LAMAN.* |
|
Ім’я вхідного файлу: |
LAMAN.DAT |
|
Ім’я вихідного файлу: |
LAMAN.SOL |
|
Максимальний час роботи на одному тесті: |
1 секунда |
Шоколадна плитка являє собою сітку з горизонтальних та вертикальних ліній, точки якої в декартовій системі координат на площині позначено точками з цілими координати. Потрібно поділити шоколадну плитку наступним чином:
- починати з лівого нижнього кута, який
знаходиться в початку координат;
- можна пересуватися вздовж цих прямих;
- при проходженні через точку завжди змінювати напрям швидкості на перпендикулярний.
Знайти мінімальну довжину шляху до верхньої правої точки.
Технічні умови. Програма Laman читає з файлу розміри шоколадної плитки (цілі числа, не більші 10^100000). Числа розділено пропуском. Програма виводить на екран єдине число - шукану величину.
Приклади файлів
Р
|
LAMAN.DAT |
LAMAN.SOL |
|
2 3 |
5 |
Розв’язок
Для одинакової парності (n,m - парні, n,m - непарні) k=максимум(n,m).
Для різної парності (n-непарне та m - парне, n=парне та m - непарне) k=максимум(n,m)-1.
Передбачити використання довгої арифметики (порівняння, множення на 2). Програма uses math; var rez,n,m:int64;
a,b,c:array[0..1000000] of byte; os,max,i,j:integer;
s,ic:char; begin
assign(input,’LAMAN.dat’);
reset(input); repeat read(s);
if s in [‘0’..’9’] then begin
for i:=a[0] downto 1 do a[i+1]:=a[i]; a[1]:=ord(s)-ord(‘0’); a[0]:=a[0]+1; end;
until s=‘ ‘;
while not(eof(input)) do begin read(s);
if s in [‘0’..’9’] then
begin
for i:=b[0] downto 1 do b[i+1]:=b[i]; b[1]:=ord(s)-ord(‘0’); b[0]:=b[0]+1;
end; end; close(input); if a[0]>b[0] then max:=1; if b[0]>a[0] then max:=2; if a[0]=b[0] then
begin i:=a[0];
while a[i]=b[i] do i:=i-1; if a[i]>b[i] then max:=1; if b[i]>a[i] then max:=2; end; end.
Задача 4. «Білі плями»
|
Ім’я файлу програми: |
WHITE.* |
|
Ім’я вхідного файлу: |
WHITE.DAT |
|
Ім’я вихідного файлу: |
WHITE.SOL |
|
Максимальний час роботи на одному тесті: |
1 секунда |
Кондитерська фабрика випустила чорно-білий шоколад. Програмістам доручили порахувати вміст білого шоколаду. Співробітники фабрики зберігають інформацію про шоколадну плитку в комп’ютері у вигляді матриці розмірністю M x N. Комірка матриці містить 0, якщо шоколад чорний та 1, якщо білий (2 ≤ M, N ≤ 100). У матриці комірки входження білого шоколаду не можуть дотикатися одна до одної ні сторонами, ні кутами.
Завдання. Написати програму, яка знаходитиме загальну кількість плям білого шоколаду та кількість плям з однаковою площею.
Вхідні дані. Вхідний текстовий файл
WHITE.DAT містить в першому рядку два числа M та N, далі слідують M рядків, у кожному по N цілих чисел розділених пропусками – елементи матриці.
Вихідні дані. Вихідний текстовий файл WHITE.SOL містить у першому рядку ціле число k - загальну кількість білих плям, далі у кожному з рядів міститься по два числа, перше – площа плями білого шоколаду, друге – їх кількість. Дані посортувати по площах в порядку зростання.
Приклади файлів
|
WHITE.DAT |
WHITE.SOL |
|
5 5 1 0 1 0 0 0 0 1 1 0 1 0 0 0 0 1 0 0 0 1 1 0 1 0 1 |
5 1 2 2 1 3 2 |
Розв’язок
Визначення кількості плям та їх площ можна здійснити за допомогою стандартного алгоритму залиття області, наприклад, рекурсивного. Такий алгоритм передбачає створення допоміжного алгоритму залиття області, що складається з таких дій:
1) Зафарбувати потрібну комірку (змінити її значення)
2) Для всіх сусідніх комірок виконати такі дії:
якщо комірка містить 1, то викликати допоміжний алгоритм для цієї комірки.
Для знаходження площі області необхідно відповідну величину збільшувати на 1 при кожному зафарбовуванні комірки.
Допоміжний алгоритм викликається, коли в процесі переглядання елементів матриці буде знайдено нову пляму (комірку матриці, значення якої дорівнює 1). При цьому при кожному виклику збільшуємо на 1 кількість плям.
Рекурсії у залитті області можна уникнути, якщо використовувати стек для зберігання комірок, що входять в область.
Для зберігання площ плям можна використати масив, у який заносити відповідні значення. Перед виведенням результатів цей масив слід упорядкувати за неспаданням, а при виведенні кілька однакових значень масиву (вони йтимуть одне за одним) замінювати на пару: значення — кількість однакових. Інший спосіб ґрунтується на створенні масиву індекси якого відповідатимуть можливим значенням площі (від 1 до m n), а значення — кількість відповідних площ плям на карті. При одержанні площі плями s збільшується на 1 значення елементу масиву з індексом s. При виведенні достатньо вивести індекси і значення ненульових елементів масиву, проглядаючи його з першого елемента.
Процедура рекурсивного визначення площі фігури може мати приблизно такий вигляд:
procedure zaliv(i,j:byte; var s:integer);
begin
a[i,j]:=2; s:=s+1; if (i+1<=n)and(a[i+1,j]=1) then zaliv(i+1,j,s); if (j+1<=m)and(a[i,j+1]=1) then zaliv(i,j+1,s); if (j-1>0)and(a[i,j-1]=1) then zaliv(i,j-1,s); if (i-1>0)and(a[i-1,j]=1) then zaliv(i-1,j,s); end;
n і m - число стовпців і рядків в розглянутій матриці, i, j - координати знайденої клітки фігури, s - змінна, в якій накопичується площа фігури. Процедура враховує знайдену клітку в площі, потім перевіряє чи заштрихована клітка, яка розташована нижче поточної (якщо це не останній рядок), і якщо так, то рекурсивно викликається з цієї клітини, потім той же процес повторюється для клітин розташованих праворуч, ліворуч і зверху від розглянутої.
Робоча частина основної програми буде мати вигляд:
max:=0; im:=0; jm:=0; for i:=1 to n do for j:=1 to m do if a[i,j]=1 then begin s:=0;
zaliv(i,j,s);
if s>max then begin max:=s; im:=i; jm:=j; end; end; writeln(‘Smax=‘,max,’ im=‘,im,’ jm=‘,jm); max - змінна, в якій зберігається максимальна площа фігури, im, jm - координати першої знайденої точки цієї фігури.
Скористуватися рекурсивним методом зафарбовування в інший колір (наприклад 2) всі сусідні
точки до i,j які рівні 1
|
|
i-1,j |
|
|
i,j-1 |
i,j |
i,j+1 |
|
|
i+1,j |
|
Рахувати кількість і заповнювати допоміжний масив, де порядковий номер відповідає за розмір плями.
Програма
program oil;
{$APPTYPE CONSOLE}
var a:array[0..101,0..101] of integer; b:array[0..100] of integer; k,s,i,j,n,m:integer; procedure pr(x,y:integer); begin
a[x,y]:=2; s:=s+1; if a[x-1,y]=1 then pr(x-1,y); if a[x+1,y]=1 then pr(x+1,y); if a[x,y-1]=1 then pr(x,y-1); if a[x,y+1]=1 then pr(x,y+1);
end; begin assign(input,’WHILLE.DAT’); reset(input); assign(output,’ WHILLE L.SOL’); rewrite(output); readln(n,m); for i:=1 to n do for j:=1 to m do read(a[i,j]); k:=0; s:=0; for i:=1 to n do for j:=1 to m do if a[i,j]=1 then begin b[s]:=b[s]+1; k:=k+1; s:=0; pr(i,j);
end; writeln(k); for i:=1 to n do if b[i]<>0 then writeln(i,’ ‘,b[i]); close(input); close(output); end.
Список використаних джерел 1. Білоусова Л.І. Краса простих задач або до питання про використання мов програмування у навчанні школярів інформатики // Комп’ютер у школі та сім’ї. – 2014. - №1. – С.18-22 2.
2. Бондарев В.М., Рублинецкий В.И., Качко Е.Г. Основы программирования. Харьков: Фолио; Ростов н/Д: Феникс, 1997. ― 368 с.
3. Бондаренко С.М. Збірник задач та розв´язків ІІ етапу Всеукраїнської учнівської олімпіади з інформатики 2014-2015 навчального року / С.М. Бондаренко, В.В. Зуб,
Ю.М. Літош. – Чернігів: ЧОІППО імені К.Д. Ушинського,
2015. – 35 с.
4. Караванова Т.П. Інформатика: основи алгоритмізації та програмування: 777 задач з рекомендаціями та прикладами: Навч. посіб. для 8-9 кл. із поглибл. вивч. інф-ки – К.: Генеза. – 2006.- 286 с.
5. Порублев И.Н., Ставровский А.Б. Алгоритмы и программы. Решение олимпиадных задач – М.: ООО "И.Д. Вильямс", 2007.
6. Попов В.Б. Turbo Pascal для школьников: Учеб. Пособие.- 3-е доп. изд. - М.: Финансы и статистика, 2002.
7. Інтернет-портал організаційно-методичного забезпечення дистанційних олімпіад з програмування для обдарованої молоді навчальних закладів України
[Електронний ресурс]. – Режим доступу: http://eolymp.com/ - Назва з екрану.
про публікацію авторської розробки
Додати розробку