Зразки розв’язування завдань. Прогресії
Прогресії
- В арифметичній прогресії а1=2,1; а10=12,9. Знайти різницю прогресії.
Розв’язання:
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b1=2,56; b4=4,42368. Обчислити знаменник прогресії.
Розв’язання:
![]()
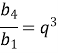
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
- В арифметичній прогресії а1=20,1; d=1,3. Обчислити суму перших восьми членів прогресії.
Розв’язання:
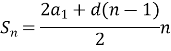
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b1=1,5; q=1,2. Обчислити суму перших чотирьох членів прогресії.
Розв’язання:
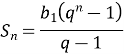
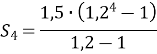
![]()
Відповідь: ![]() .
.
-
Дано прогресію 23,5;
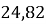 ; 26,14; … знайти сьомий член даної прогресії.
; 26,14; … знайти сьомий член даної прогресії.
Розв’язання:
![]()
![]()
![]()
Отже дана послідовність є арифметичною прогресією.
![]()
![]()
![]()
Відповідь: ![]() .
.
- Дано прогресію 1,5;1,8; 2,16; … Обчислити четвертий член даної прогресії.
Розв’язання:
![]()
![]()
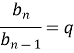
Отже дана послідовність є геометричною прогресією.
![]()
![]()
![]()
Відповідь: ![]() .
.
- Дано прогресію 2,1; 3,3; 4,5; … Обчислити номер члена прогресії, який дорівнює 11,7.
Розв’язання:
![]()
![]()
Отже це є арифметична прогресія, різниця якої d=1,2.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: Дане число є дев’ятим членом арифметичної прогресії.
- Дано прогресію 1,2; 1,8; 2,7; … Обчислити номер члена прогресії, що дорівнює 4,05.
Розв’язання:
![]()
![]()
Отже ми маємо геометричну прогресію, знаменник якої q=1,5.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: задане число є четвертим членом геометричної прогресії.
- В арифметичній прогресії а5=14,91; а9=20,11. Обчислити а1.
Розв’язання:
Складемо систему рівнянь і розв’яжемо її.
![]()
![]()
![]()
![]()
![]() .
.
Відповідь: ![]() .
.
- В арифметичній прогресії а7=12,01; а11=17,61. Обчислити різницю прогресії.
Розв’язання:
Складемо систему рівнянь і розв’яжемо її.
![]()
![]()
![]()
Відповідь: ![]() .
.
- В геометричній прогресії b5=64; b8=1. Обчислити b3.
Розв’язання:
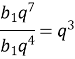
![]()
![]()
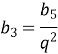
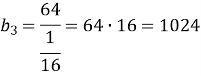
Відповідь: ![]() .
.
- В арифметичній прогресії а9+а15=14,8. Обчислити а12.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
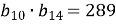 . Обчислити
. Обчислити 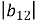 .
.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
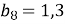 . Обчислити
. Обчислити 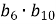 .
.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
- Обчислити суму перших п’ятнадцяти непарних чисел.
Розв’язання:
Маємо арифметичну прогресію ![]() .
.
![]()
Відповідь: ![]() .
.
- Обчислити перший член арифметичної прогресії, якщо сума перших дванадцяти членів дорівнює 642, а дванадцятий член дорівнює 48.
Розв’язання:
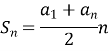
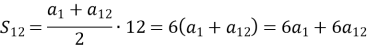
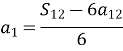
![]()
Відповідь: ![]() .
.
-
Обчислити знаменник геометричної прогресії, яка складається з дійсних чисел, якщо
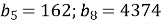 .
.
Розв’язання:
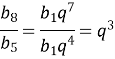
![]()
![]()
Відповідь: ![]() .
.
- В арифметичній прогресії а9=12,4; а23=4,7. Знайти а14+а17.
Розв’язання:
У арифметичній прогресії суми рівновіддалених членів рівні.
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
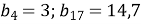 . Обчислити
. Обчислити 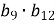 .
.
Розв’язання:
У геометричній прогресії добутки рівновіддалених членів рівні.
![]()
![]()
Відповідь: ![]() .
.
-
Сума п перших членів арифметичної прогресії виражається формулою
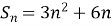 . Знайти а6.
. Знайти а6.
Розв’язання:
Знайдемо ![]() і
і ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
-
Сума п перших членів арифметичної прогресії виражається формулою
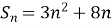 . Знайти різницю прогресії.
. Знайти різницю прогресії.
Розв’язання:
![]()
![]()
![]()
![]()
Відповідь: ![]() .
.
-
В арифметичній прогресії
 Знайти
Знайти 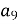 .
.
Розв’язання:
![]()
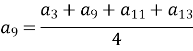
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
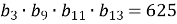 . Обчислити
. Обчислити 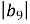 .
.
Розв’язання:
![]()
![]()
![]()
Відповідь: ![]() .
.
-
В арифметичній прогресії
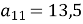 . Обчислити
. Обчислити 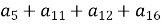 .
.
Розв’язання:
![]()
![]()
Відповідь: ![]() .
.
-
В геометричній прогресії
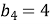 . Обчислити
. Обчислити 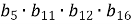 .
.
Розв’язання:
![]() .
.
![]()
Відповідь: ![]() .
.


про публікацію авторської розробки
Додати розробку
