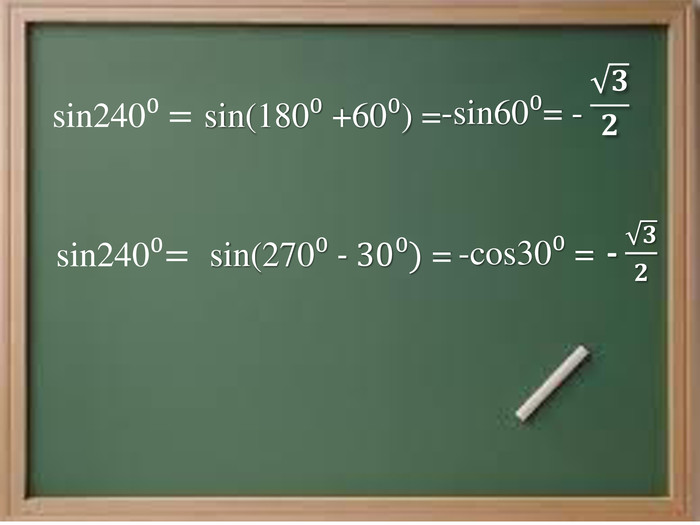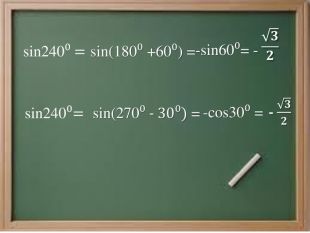1. Конспект уроку з алгебри та початків аналізу для 10класу на тему "Формули зведення"; 2.Презентація до уроку "Формули зведення"
Тема уроку: Формули зведення
Мета уроку: навчальна: закріпити знання учнів з теми «Властивості тригонометричних функцій числового аргументу», уміння виконувати тотожні перетворення тригонометричних виразів, використовуючи вивчені тригонометричні тотожності.
Ввести формули зведення, формувати уміння учнів застосовувати вивчені формули для спрощення виразів та обчислень.
розвивальна: розвивати вміння застосовувати знання в конкретній ситуації; сприяти розвитку вміння аналізувати, порівнювати, робити вірні логічні висновки; розвивати логічне мислення, самостійність в діяльності учнів; формувати практичну та соціальну компетентності через уміння застосовувати знання, співпрацювати та допомагати один одному; розвивати наполегливість, увагу та зосередженість, зацікавленість у результаті роботи.
виховна: виховувати толерантне ставлення один до одного, вміння співпрацювати, підтримувати, допомагати один одному, вміння раціонально використовувати робочий час, працьовитість, старанність, відповідальність; підвищувати інтерес до предмету. Продовжити виховання патріотизму, почуття гордості за свою Батьківщину, почуття відповідальності за свої рішення.
Тип уроку: засвоєння нових знань.
Обладнання уроку: Макет одиничного кола, таблиця значень тригонометричних функцій, картки, екран, м/м проектор.
Очікувані результати: учням необхідно
- знати: - мнемонічне правило формул зведення;
- алгоритм користування цим правилом;
- вміти : - свідомо користуватися правилом формул зведення для тотожних перетворень тригонометричних виразів та обчислень;
План уроку
І. Організаційний момент.
ІІ. Перевірка домашнього завдання.
ІІІ. Мотивація навчання.
ІV. Актуалізація опорних знань учнів;
V. Сприймання і усвідомлення нового матеріалу.
VІ. Формування умінь і навиків
VІІ. Систематизація знань. Самостійна робота.
VІІІ. Рефлексія. Підсумок уроку.
ІХ. Домашнє завдання.
Як приємно дізнатися, що ти чогось навчився.
Мольєр
Хід уроку
І. Організаційний момент.
Привітання шановним гостям. Читаємо епіграф уроку, налаштовуємося на плідну роботу.
ІІ. Перевірка домашнього завдання.
- Учні працюють у домашніх групах, кожна з яких мала завдання:
Спростити вирази, використовуючи формули додавання: І. 
, ІІ. 
,
ІІІ. 
, ІV. 
, V. 
.
Представник кожної групи записує завдання на дошці. Результати зберігаємо на дошці.
- В цей час перевіряю теоретичні знання учнів з теми.
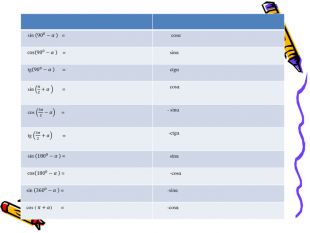
Технологія: «Закінчи речення»
- Синус числа α, це ….
- Косинус числа α, це ….
- Тангенс числа α, це ….
- Котангенс числа α, це ….
-
Найбільше та найменше значення функцій
, 
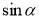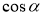дорівнює..
-
Найбільше та найменше значення функцій
, 
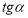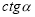дорівнює..
- Парними серед тригонометричних функцій є…
- Непарними серед тригонометричних функцій є…
-
Найменшим додатнім періодом функцій
,
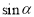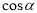є число…
-
Найменшим додатнім періодом функцій 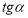, 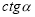є число…
- Якщо cos α > 0, а sin α < 0 , то α є число … четверті;
-
Якщо tg
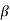> 0; cos 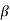< 0, то 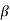є число … четверті.
Гра «Математичні пазли» (перевірка знання основних тригонометричних тотожностей)
Кожна група отримує набір карточок, на одних з яких записана І частина формули, а на інших – її права частина. Карточки у довільному порядку. Завдання групам: на швидкість розставити карточки правильно.
(Команда, яка перша справиться з завданням отримує 5 балів, решта залежно від швидкості і правильної відповіді).
Підводимо підсумок домашнього завдання.
ІІІ. Мотивація навчальної діяльності учнів, повідомлення теми та мети уроку
- Слово викладача:
Розв’язання багатьох алгебраїчних задач істотно спрощується, якщо ми володіємо і виконуємо рівносильні або тотожні перетворення, тобто діємо за законами математики.
Тригонометричні функції зв’язані між собою великою кількістю співвідношень. Але не завжди їх треба зазубрювати, можливо достатньо володіти ланцюжком міркувань, тобто певним алгоритмом, щоб спростити даний вираз.
“Алгебра щедра, вона часто дає більше, ніж у неї просять”, так стверджував великий математик Д′Аламбер.
Сподіваюсь, що наш урок буде тому підтвердженням. Сьогодні ми вивчимо формули зведення, які дозволяють подати значення тригонометричних функцій будь-якого кута 
(
) через відповідні значення тригонометричних функцій гострого кута. Це значно спрощує тотожні перетворення виразів. На уроці ми встановимо зв´язки між формулами зведення із вивченим на попередніх уроках матеріалом.
Та, давайте, спочатку повторимо опорні факти, які будемо застосовувати при вивченні нового матеріалу.
ІV. Актуалізація опорних знань учнів
Слова вчителя: Будь-яка наука могла б пишатися такою історією, як історія математики, тому що вона менш за все історія помилок. Але мудрі люди кажуть “ Не помиляється той, хто нічого не робить”, або “ На помилках вчаться”.
- «Знайди помилку» (слайди 7,8)
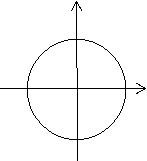
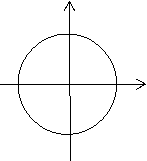1) у у у
- + х + + + -
- + О х О х
у=sin x - - у=cos x - + у=tg x
2) а) 90⁰+α ∊ ІІ чв.. в) 180⁰
ІІ чв..
б) 
+α 
ІІІ чв.. г) 2
- α І чв..
в) 
- α І чв.. д) 
ІV чв.
3) а) tg 170º 
; б) cos 200º 
; в) ctg (π+α) ; г) sin( - α) 
д) cos(180⁰-
.
- Хто швидше? (слайд 9)
Обчислити: а) sin
;
б) cos(-60⁰); в) tg(-
;
г) cos 750⁰; д) ctg225⁰.
Відкриваю відповіді для перевірки (слайд 10)
- Фізкультхвилика
Називаю граничні кути, а учні поворотом голови вверх-вниз, вліво-вправо показують на якій осі вони закінчуються .
90⁰; 2π; 180⁰; 
360⁰; 
-π;-270⁰.
- Технологія «Мозковий штурм»:
Обчислити: sin240⁰
Учні пропонують способи обчислення останнього прикладу, вислуховуємо кожного і приходимо до висновку, що на обчислення даного виразу потрібен певний час. А чи не можна зробити це швидше?
V. Сприймання і усвідомлення нового матеріалу.
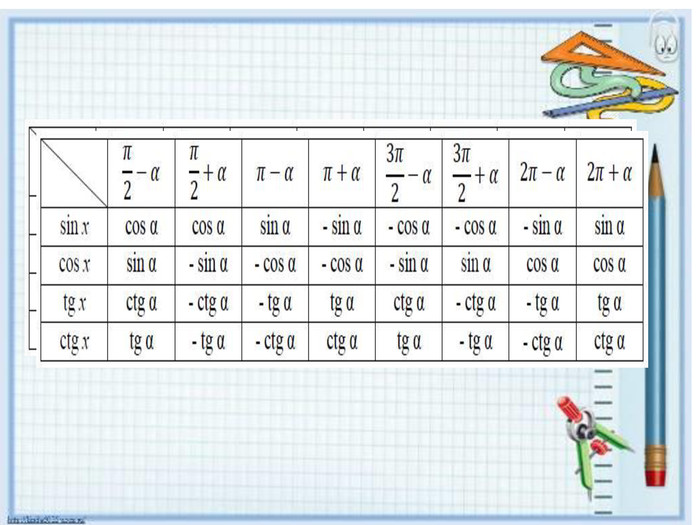
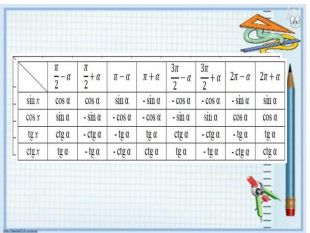
1. Формули зведення – це формули, що виражають тригонометричні функцій кутів (чисел)
|
|
|
|
sin |
cosα |
|
|
sinα |
|
tg |
ctgα |
|
sin |
cosα |
|
cos |
- sinα |
|
tg |
-ctgα |
|
sin |
sinα |
|
|
-cosα |
|
sin |
-sinα |
|
cos ( |
-cosα |
, 
, 
, 
через тригонометричні функції кута (числа) α, де α – довільний кут (число).
А скільки їх всього? Давайте порахуємо. (слайд 13)
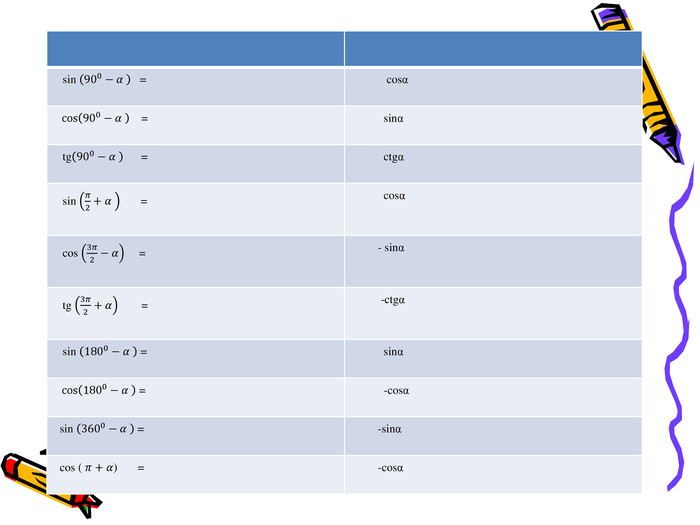
Деякі з цих формул вам відомі з курсу геометрії, а деякі ви отримали, виконуючи домашнє завдання:
(слайд 14)
Пропоную встановити закономірність у цих формулах і відповісти, як швидко можна отримати результат,
не виконуючи перетворень цих виразів.
Учні формулюють правило, викладач коригує його:
1. Якщо в лівій частині формули кут дорівнює 
, 
, то синус змінюється на косинус, тангенс на котангенс і навпаки. Якщо кут дорівнює 
, 
, то зміна не відбувається.
2. В правій частині формули ставимо знак, який має ліва частина при умові 
. Це правило називається мнемонічним (пояснюю чому).
Звертаю увагу, як легко запам’ятати І частину правила
(кивком голови - да (змінюється), ( 
, 
- вісь ОУ), поворотом голови – ні (не змінюється), ( 
вісь ОХ))
Пропоную учням записати короткий запис: (слайд 15 )
|
1.
2. Знак правої частини визначається по знаку лівої.
|
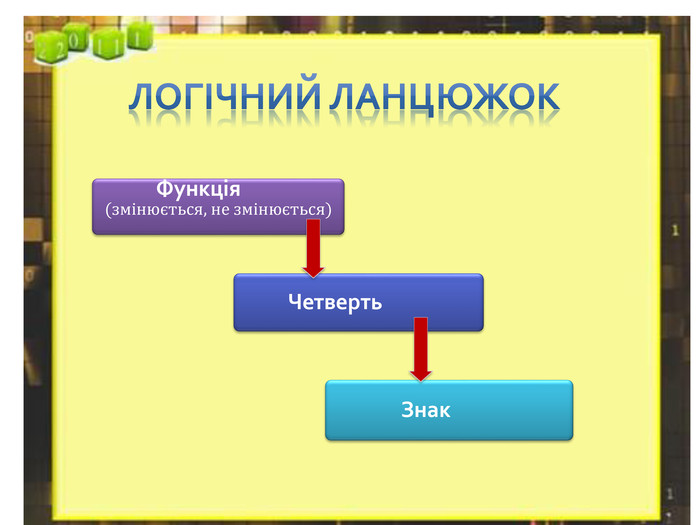
Починаючи роботу з формулами зведення, прошу учнів запам'ятати такий логічний ланцюжок (на кожному робочому столі короткий запис правила та логічний ланцюжок)
Функція (змінюється, не змінюється) Чверть Знак
Приклади: 1. Спростити вирази (колективно під керівництвом викладача):
а) 
; в) 
;
б) соs
; г) 
;
д) cos2 
; е) sin2(π –α),
2. Спростіть вираз: sin
∙ соs (
- α) - соs
sin(+ α);
3. Повертаємось до обчислення значення виразу sin240⁰ (слайд 17) .
Як застосувати формули зведення до розв’язання цієї проблеми?
VI. Формування вмінь і відпрацьовування навичок
- Робота у домашніх групах: (слайд 18)
1) Спростіть вираз:
а) sin2 (180° - х) + sin2 (270° - х) + tg2(90°+ х);
2) Обчисліть: а) tg300°;
Перевіряємо роботу по зарані записаним відповідям. (слайд 19)
- Після цієї роботи пропоную учням згрупуватися у групи по кольору.
Інтерактивна вправа «Оціни свою роботу»
Оцініть свою роботу і підніміть кольорові картки :
- зелений - все зрозумів, можу рухатись далі;
- жовтий - ще виникають деякі труднощі, потрібно попрацювати над даним матеріалом;
- червоний - було складно, потрібна допомога вчителя.
Завдання для «зелених»: а) Довести тотожність:
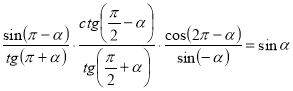
б) Знайти значення виразу:
cos80° cos40° - sin80°sin40°
Завдання для «жовтих»: Спростіть вираз:
tg ( - α ) – ctg ( π + α) + sin ( 
+ α ) + сos (4π + α )
Завдання для «червоних»: (працюють за підтримки викладача)
а) соs
+ sin
; б) сtg
∙ сtg
;
Кожна група захищає свою роботу.
VІІ. Рефлексія
У кожного учня на столі карточка для самооцінки своєї роботи на уроці, вони заповнюють їх та здають для оцінки вчителю.
VІІІ. Домашнє завдання:
- Вивчити правило формул зведення;
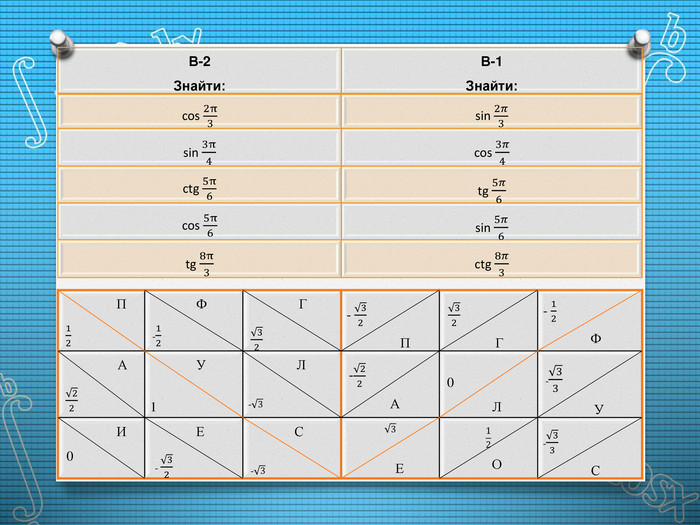
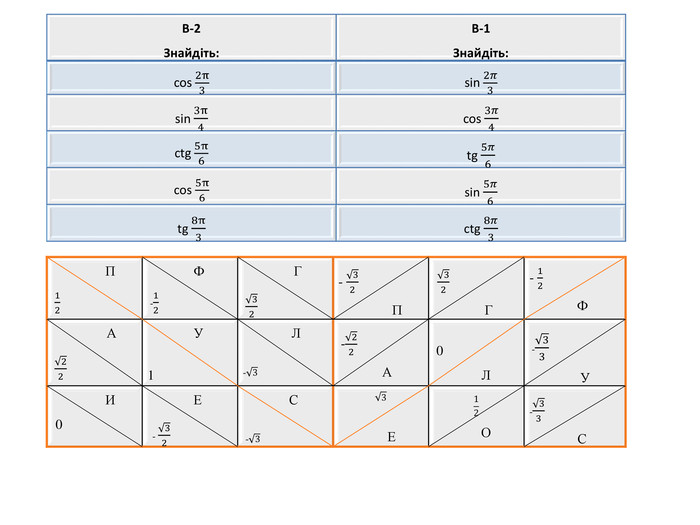
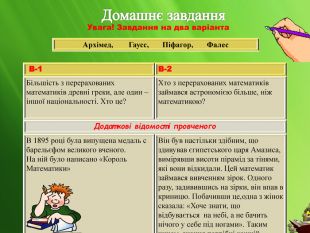
- (робота у домашніх групах) (слайд 22-24 )
Архимед, Гаусс, Пифагор, Фалес
В-1
Більшість з перерахованих математиків древні греки, але один - іншої національності. Хто це?
В-2
Хто з перерахованих математиків займався астрономією, більше ніж математикою?
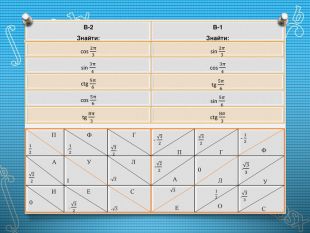
Кожна група отримує роздруковане завдання.
|
В-2 Знайдіть: |
В-1 Знайдіть: |
|
cos |
sin |
|
sin |
cos |
|
ctg |
tg |
|
cos |
sin |
|
tg |
ctg |
|
П
|
Ф
- |
Г
|
-
П |
Г |
-
Ф
|
|
А
|
У
1 |
Л
- |
- |
0 Л |
-
|
|
И
0 |
Е
- |
С
- |
Е |
О |
-
С |
Індивідуально: Довести тотожність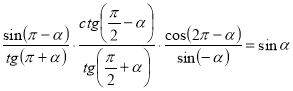
Тема уроку: Формулизведення. Підготувала викладач математики. ДПТНЗ “Ізмаїльське вище професійне училище” Бойченко Р. М.
Очікувані результати: учням необхідно знати: - мнемонічне правило формул зведення; - алгоритм користування цим правилом; вміти:- свідомо користуватися правилом формул зведення для тотожних перетворень тригонометричних виразів та обчислень;
План урокуІ. Організаційний момент.ІІ. Перевірка домашнього завдання.ІІІ. Мотивація навчання.ІV. Актуалізація опорних знань учнів;V. Сприймання і усвідомлення нового матеріалу. VІ. Формування умінь і навиків. VІІ. Систематизація знань. Самостійна робота. VІІІ. Рефлексія. Підсумок уроку.ІХ. Домашнє завдання
Як приємно дізнатися, що ти чогось навчився. Мольєр
“ Алгебра щедра, вона часто дає більше, ніж у неї просять”, так стверджував великий французський математик д'Аламбер.
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} sin 900−𝛼 = cosα cos900−𝛼 =sinα tg900−𝛼 =ctgα sin 𝜋2+𝛼 =cosα cos 3𝜋2−𝛼=- sinα tg 2π−𝛼=-tgα sin 1800−𝛼= sinα cos1800−𝛼 =-cosα sin 3600−𝛼 =-sinα cos ( 𝜋+𝛼)=-cosα{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}cosαsinαctgαcosα- sinα-tgα sinα-cosα-sinα-cosα{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} sin 900−𝛼 = cosα cos900−𝛼 =sinα tg900−𝛼 =ctgα sin 𝜋2+𝛼 =cosα cos 3𝜋2−𝛼=- sinα tg 2π−𝛼=-tgα sin 1800−𝛼= sinα cos1800−𝛼 =-cosα sin 3600−𝛼 =-sinα cos ( 𝜋+𝛼)=-cosα{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}cosαsinαctgαcosα- sinα-tgα sinα-cosα-sinα-cosα
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1. «Знайди помилку» 1) а) - + б) + + в) - + о х о х о х - + - - - - у=sin x у=cos x у=tg x
1. «Знайди помилку» 2) а) 90⁰+α ∊ ІІ чв.. г) 180⁰+𝜶∈ ІІ чв.. б) 𝟑𝝅𝟐 +α ∈ ІІІ чв.. д ) 2𝝅 - α ∈ І чв.. в) 𝝅𝟐 - α ∈ І чв.. е) 𝟑𝛑𝟐−𝜶 ∈ ІV чв.
2. Хто швидше?Обчислити: а) sin𝝅𝟒; б) cos(-60⁰); в) tg(-𝝅𝟑); г) cos 750⁰; д) ctg225⁰;
Відповідь:а) sin𝝅𝟒 = 𝟐𝟐; б) cos(-60⁰) = 𝟏𝟐; в) tg(-𝝅𝟑) = -𝟑; г) cos 750⁰ = cos (360⁰∙2+30⁰)= cos30⁰=𝟑𝟐;д) ctg225⁰ = ctg(180⁰+45⁰) = ctg45⁰=1
Фізкультхвилинка
{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Формулы приведения – это формулы, которые выражают тригонометрические функции углов (чисел) 𝝅𝟐± α, 𝟑𝝅𝟐± α, 𝝅 ± α, 2π ± α через тригонометрические функции угла (числа) α, где α – произвольный угол (число).{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Формули зведення– це формули, що виражають тригонометричні функцій кутів (чисел) 𝝅𝟐± α, 𝟑𝝅𝟐± α, 𝝅 ± α, 2π ± α через тригонометричні функції кута (числа) α, де α – довільний кут (число).{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}
sin 900−𝛼 = cosα cos900−𝛼 = sinα tg900−𝛼 = ctgα sin 𝜋2+𝛼 = cosα cos 3𝜋2−𝛼 = - sinα tg 3𝜋2+𝛼 = -ctgα sin 1800−𝛼 = sinα cos1800−𝛼 = -cosα sin 3600−𝛼 = -sinα cos ( 𝜋+𝛼) = -cosα cosα sinα ctgα cosα - sinα -ctgα sinα -cosα -sinα -cosα
Правило:𝝅𝟐 𝟑𝝅𝟐 π 2π{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D} 1. 𝝅𝟐 ± α, 𝟑𝝅𝟐 ± α ; (90⁰±α, 270⁰±α) - функція змінюється на кофункцію; 𝝅±𝜶, 𝟐𝝅±𝜶 ; (180⁰±α, 360⁰±α) - функція не змінюється;2. Знак правої частини визначається по знаку лівої.{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D}2. Знак правої частини визначається по знаку лівої.
Логічний ланцюжок. Логічний ланцюжок. Функція. Четверть. Знак(змінюється, не змінюється)
sin240⁰=sin240⁰ =sin(180⁰ +60⁰) =-sin60⁰= - 𝟑𝟐 sin(270⁰ - 30⁰) =-cos30⁰ =- 𝟑𝟐
Спілкуйтесь, можете радитись, допомогати один одному. Упростить выражение: sin2 (180° - х) + sin2 (270° - х) + tg2(90°+ х);2). Вычислить: а) tg300°; Работа в групах
1) Упростить выражение : sin2 (180° - х) + sin2 (270° - х) + tg2(90°+ х) = = sin2 х +cos2 х +ctg2 х = 1 + ctg2 х = 1sin2x; 2) Вычислить : tg300° = tg (270° +30°) = - сtg30° = - 3 Проверь себя!
Я ВМІЮ!Я ВМІЮ. Я ВМІЮ?
Твій настрій1.2. 3. 4.5. Дякую за урок!Самооцінка: Оцінка командира групи: Оцінка викладача:
Домашнє завдання. Увага! Завдання на два варіанта{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Архімед, Гаусс, Піфагор, Фалес {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} В-1 В-2 Більшість з перерахованих математиків древні греки, але один – іншої національності. Хто це?Хто з перерахованих математиків займався астрономією більше, ніж математикою?Додаткові відомості провченого. В 1895 році була випущена медаль с барельєфом великого вченого. На ній було написано «Король Математики» Він був настільки здібним, що здивував єгипетського царя Амазиса, вимірявши висоти пірамід за тінями, які вони відкидали. Цей математик займався вивченням зірок. Одного разу, задивившись на зірки, він впав в криницю. Побачивши це,одна з жінок сказала: «Хоче знати, що відбувається на небі, а не бачить нічого у себе під ногами». Таким чином, знання потрібні кожній людині, вони допомагають у досягненні поставлених цілей.ppt_x
{BC89 EF96-8 CEA-46 FF-86 C4-4 CE0 E7609802}В-2 Знайти: В-1 Знайти:cos 2π3sin 2𝜋3sin 3π4cos 3𝜋4ctg 5π6tg 5𝜋6cos 5π6sin 5𝜋6 tg 8π3ctg 8𝜋3{BC89 EF96-8 CEA-46 FF-86 C4-4 CE0 E7609802}В-2 Знайти: В-1 Знайти: П 12 Ф -12 Г 32 - 32 П 32 Г - 12 Ф А 22 У 1 Л -3 -22 А 0 Л -33 У И 0 Е - 32 С -33 Е12 О-33 С У 1 0 Л И 0
{BC89 EF96-8 CEA-46 FF-86 C4-4 CE0 E7609802}В-2 Знайдіть: В-1 Знайдіть:cos 2π3sin 2𝜋3sin 3π4cos 3𝜋4ctg 5π6tg 5𝜋6cos 5π6sin 5𝜋6 tg 8π3ctg 8𝜋3{BC89 EF96-8 CEA-46 FF-86 C4-4 CE0 E7609802}В-2 Знайдіть: В-1 Знайдіть: П 12 Ф -12 Г 32 - 32 П 32 Г - 12 Ф А 22 У 1 Л -3 -22 А 0 Л -33 У И 0 Е - 32 С -33 Е12 О-33 С У 1 0 Л И 0
про публікацію авторської розробки
Додати розробку