7 клас геометрія конспект учня".Рівнобедрений трикутник"

Конспект учня

Тема:  Рівнобедрений трикутник та його властивості

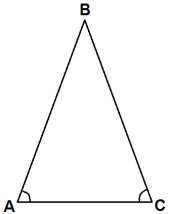
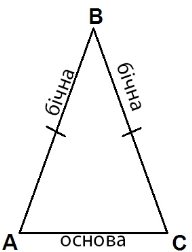
 Трикутник називають рівнобедреним, якщо у нього дві сторони рівні.

АВС – рівнобедрений

АВ і ВС – бічні сторони

АС – основа

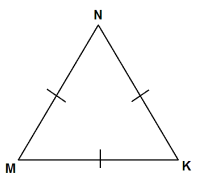Трикутник, всі сторони якого рівні, називають рівностороннім.

MNK – рівносторонній

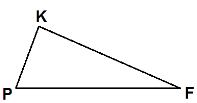Трикутник, всі сторони якого мають різну довжину, називають різностороннім.

KPF - різносторонній

 Залежно від сторін, розрізняють такі види трикутників: різносторонні, рівнобедрені, рівносторонні

Теорема 1 (властивість кутів рівнобедреного трикутника)

У рівнобедреному трикутнику кути при основі рівні.

Доведення

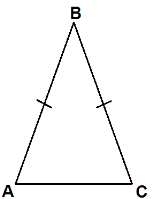АВС – рівнобедрений, АС – основа.

Доведемо, що А=С.

АВС = СВА (за першою ознакою), оскільки АВ = ВС, СВ = ВА,

• В – спільний для АВС і СВА.

З рівності трикутників випливає, що А=С. Теорему доведено.

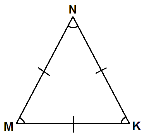Наслідок. У рівносторонньому трикутнику усі стороні рівні.

Теорема 2 (ознака рівнобедреного трикутника)

Якщо в трикутнику два кути рівні, то він рівнобедрений

Доведення

АВС - трикутник, у якого А=С.

Доведемо, що він є рівнобедреним трикутником з основою АС.

АВС=СВА (за другою ознакою)

Оскільки А=С, С=А, і АС – спільна сторона трикутників.

З рівності трикутників випливає, що АВ=ВС. Тому АВС – рівнобедрений трикутник з основою АС. Теорему доведено.

Наслідок: Якщо у трикутнику всі кути рівні, то він рівносторонній.*

*Теорема 2 є оберненою до Теореми 1.

Задача 1

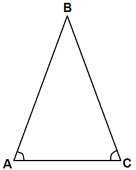У трикутнику АВС А=30^о, С=30^о.

Доведіть, що АВС – рівнобедрений.

Доведення

За ознакою рівнобедреного трикутника (теорема 2), А=С, тому АВС – рівнобедрений.

Задачу доведено.

Задача 2

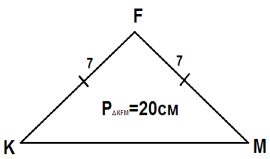KFM – рівнобедрений, КМ – основа;

KF = 7см, Р_KFM= 20 cм.

Знайдіть основу KM.

Розв`язання

KFM – рівнобедрений з основою KM,

тому KF=MF=7см – бічні сторони.

Р_KFM= KF + MF + КМ,

Отже КМ = 20-7×2= 6 (см)

Відповідь: 6 см.