8 клас КР № 4 Розв’язування прямокутних трикутників
___________________________________________________________________________________________________
8 клас КР № 4 Розв’язування прямокутних трикутників Варіант І
-
 Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 5 см і 12 см.
Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 5 см і 12 см.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
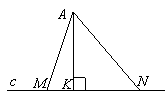
Укажіть за малюнком проекцію похилої
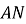 на пряму
на пряму 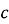 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
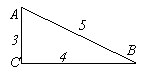
Для трикутника
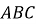 , зображеного на малюнку, знайдіть
, зображеного на малюнку, знайдіть 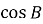 .
.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
- Сторони ромба 17 см, а одна з його діагоналей – 16 см. Знайдіть другу діагональ ромба.
-
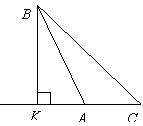 Точка знаходиться на відстані 8 см від прямої. Із цієї точки до прямої проведено похилу, яка утворює з прямою кут
Точка знаходиться на відстані 8 см від прямої. Із цієї точки до прямої проведено похилу, яка утворює з прямою кут 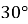 . Знайдіть довжину похилої та довжину проекції похилої на пряму.
. Знайдіть довжину похилої та довжину проекції похилої на пряму.
-
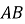 – гіпотенуза прямокутного трикутника
– гіпотенуза прямокутного трикутника 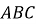 ,
, 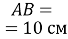 ,
, 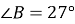 . Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
. Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
-
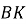 – висота трикутника
– висота трикутника 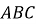 ,
, 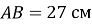 ,
, 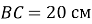 ,
, 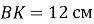 . Знайдіть
. Знайдіть 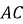 .
.
-
У трикутнику
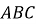 (
( )
) 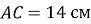 ,
, 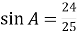 . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
- Бісектриса гострого кута прямокутного трикутника ділить катет на відрізки 3 см і 5 см. Знайдіть гіпотенузу трикутника.
___________________________________________________________________________________________________
8 клас КР № 4 Розв’язування прямокутних трикутників Варіант ІІ
-
 Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 13 см, а другий катет – 5 см.
Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 13 см, а другий катет – 5 см.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
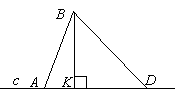
Укажіть за малюнком проекцію похилої
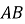 на пряму
на пряму 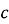 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
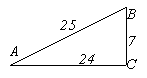
Для трикутника
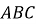 , зображеного на малюнку, знайдіть
, зображеного на малюнку, знайдіть 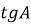 .
.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
- Діагоналі ромба дорівнюють 6 см і 8 см. Знайдіть сторони ромба.
-
Точка знаходиться на відстані 6 см від прямої. Із цієї точки до прямої проведено похилу, яка утворює з прямою кут
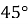 . Знайдіть довжину похилої та довжину проекції похилої на пряму.
. Знайдіть довжину похилої та довжину проекції похилої на пряму.
-
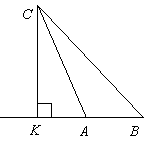 Трикутник
Трикутник 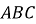 – прямокутний (
– прямокутний ( ),
), 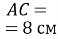 ,
, 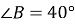 . Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
. Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
-
 – висота трикутника
– висота трикутника 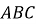 ,
, 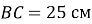 ,
, 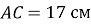 ,
, 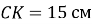 . Знайдіть
. Знайдіть 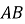 .
.
-
У трикутнику
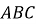 (
( )
) 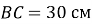 ,
, 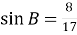 . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
- Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки 30 см і 40 см. Знайдіть менший катет трикутника.
___________________________________________________________________________________________________
___________________________________________________________________________________________________
8 клас КР № 4 Розв’язування прямокутних трикутників Варіант ІІІ
-
 Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 6 см і 8 см.
Знайдіть гіпотенузу прямокутного трикутника, катети якого дорівнюють 6 см і 8 см.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
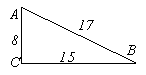
Укажіть за малюнком проекцію похилої
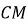 на пряму
на пряму  .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
Для трикутника
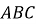 , зображеного на малюнку, знайдіть
, зображеного на малюнку, знайдіть 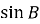 .
.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
- Сторони ромба – 13 см, а одна з його діагоналей – 10 см. Знайдіть другу діагональ ромба.
-
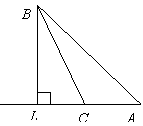 З точки до прямої проведено перпендикуляр і похилу, що утворює кут
З точки до прямої проведено перпендикуляр і похилу, що утворює кут 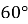 із прямою. Знайдіть довжину перпендикуляра та довжину похилої, якщо проекція похилої дорівнює 3 см.
із прямою. Знайдіть довжину перпендикуляра та довжину похилої, якщо проекція похилої дорівнює 3 см.
-
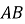 – гіпотенуза прямокутного трикутника
– гіпотенуза прямокутного трикутника 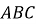 ,
, 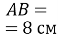 ,
, 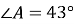 . Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
. Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
-
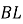 – висота трикутника
– висота трикутника 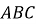 ,
, 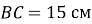 ,
, 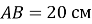 ,
, 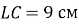 . Знайдіть
. Знайдіть 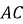 .
.
-
У трикутнику
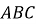 (
( )
) 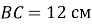 ,
,  . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
- Бісектриса гострого кута прямокутного трикутника ділить катет на відрізки 26 см і 10 см. Знайдіть інший катет трикутника.
___________________________________________________________________________________________________
8 клас КР № 4 Розв’язування прямокутних трикутників Варіант ІV
-
 Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 10 см, а другий катет – 6 см.
Знайдіть катет прямокутного трикутника, якщо його гіпотенуза дорівнює 10 см, а другий катет – 6 см.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
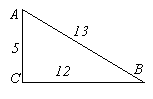
Укажіть за малюнком проекцію похилої
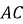 на пряму
на пряму 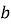 .
.
 А.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
-
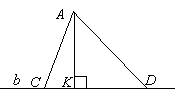
Для трикутника
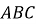 , зображеного на малюнку, знайдіть
, зображеного на малюнку, знайдіть 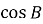 .
.
А. ![]() . Б.
. Б. ![]() . В.
. В. ![]() . Г.
. Г. ![]() .
.
- Діагоналі ромба дорівнюють 14 см і 48 см. Знайдіть сторони ромба.
-
З точки до прямої проведено перпендикуляр і похилу, що утворює кут
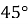 із прямою. Знайдіть довжину перпендикуляра та довжину похилої, якщо проекція похилої дорівнює 4 см.
із прямою. Знайдіть довжину перпендикуляра та довжину похилої, якщо проекція похилої дорівнює 4 см.
-
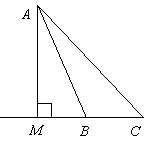 Трикутник
Трикутник 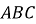 – прямокутний (
– прямокутний ( ),
), 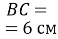 ,
, 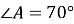 . Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
. Розв'яжіть цей прямокутний трикутник (сторони трикутника знайдіть з точністю до сотих сантиметра).
-
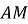 – висота трикутника
– висота трикутника 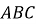 ,
, 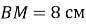 ,
, 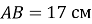 ,
, 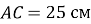 . Знайдіть
. Знайдіть 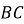 .
.
-
У трикутнику
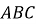 (
( )
) 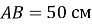 ,
, 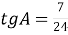 . Знайдіть периметр трикутника.
. Знайдіть периметр трикутника.
- Бісектриса прямого кута прямокутного трикутника ділить гіпотенузу на відрізки 20 см і 15 см. Знайдіть більший катет трикутника.
___________________________________________________________________________________________________


про публікацію авторської розробки
Додати розробку

-

Гура Олена Федорівна
06.02.2025 в 05:15
Велике ДЯКУЮ, Чудовий матеріал.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Пагута Данута
21.02.2024 в 18:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Троян Юлія Анатоліївна
05.03.2021 в 11:11
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
-

Троян Юлія Анатоліївна
05.03.2021 в 11:11
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 1 відгук