Урок з алгебри в 9 класі

Тема. СИСТЕМИ ЛІНІЙНИХ НЕРІВНОСТЕЙ ТА

                           ЇХ РОЗВ’ЯЗУВАННЯ

           

Мета: ознайомити учнів з поняттям «Система        нерівностей»;     

Ø          виробити вміння розв'язувати системи нерівностей з однією змінною;

Ø          розвивати логічне мислення, алгоритмічну культуру та розумову активність учнів;

Ø          виховувати любов до математики,  ініціативність, самостійність.

Обладнання: зошити, ручки, підручники, указка, комп’ютер, презентація, використовується підручник : 

А. Г. Мерзляк, В. Б. Полонський, М. С. Якір.  Алгебра:

підручник для 9кл. – Харків. - «Гімназія», 2009.

Єдиний шлях, що веде до знань – діяльність.

                                                              Б. Шоц

                                   Хід уроку

І. Організаційний етап

Привітання, рефлексія – настрій, бажання працювати   на уроці.

На минулих уроках ми зупинилися на розв'язуванні лінійних нерівностей з однією змінною. Сьогодні ознайомимося з поняттям система нерівностей і навчимося їх розв'язувати. І,  напевно, кожен із вас зрозумів, що для правильного й швидкого  розв'язування завдання потрібно багато працювати.

Тому епіграфом нашого уроку будуть слова Б. Шоца "Єдиний шлях, що веде до знань – діяльність".

ІІ. Перевірка  домашнього завдання.

А зараз перейдемо до перевірки домашнього завдання.

(діти перевіряють домашнє завдання за розв'язками на комп'ютері і заносять  відповідну  кількість балів  до картки самооцінювання).

ІІІ. Актуалізація опорних знань

1). Гра "Мікрофон"

Сьогодні до нас на урок  завітав журналіст газети «Математика», який пише статтю на  тему "Лінійні нерівності" і хоче взяти у вас інтерв'ю.

Ø      Що таке нерівність?

Ø      Нагадайте загальний вигляд   лінійної  нерівності з однією змінною.

Ø      Як ви вважаєте, що є розв'язком лінійної нерівності з однією змінною?

(значення змінної при якому дана нерівність перетворюється на правильну числову нерівність).

Ø      Як називаються ці знаки?

        ≥ ; ≤  (нестрога нерівність);         > ; <  (строга нерівність).

Ø      Історична довідка (довідку можуть підготувати учні,або вчитель).

Ø      Як позначаються на координатній прямій кінціпроміжків, що є розв'язками строгої нерівності?  (порожнім кружечком).

Ø      Як позначаються на координатній прямій кінціпроміжків, що є розв'язками нестрогої нерівності? (зафарбованим  кружечком).

Ø      У відповіді пишемо    (квадратну дужку, якщонерівність нестрога і круглу дужку,  якщо нерівність строга)

Ø      Запишіть відповіді до рисунків, на яких зображеніпроміжки, двома способами: у вигляді нерівності та числового проміжку.

 

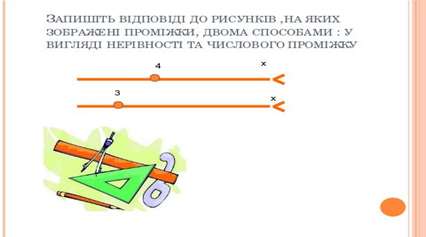
 2) Встановити відповідність між лінійною нерівністю та її розв'язком 

       

             Відповідь.1- Г; 2 -  Б ; 3 - А; 4 - В.

3)Завдання "відшукати помилку"  (на дошці).

          а).  4х – 20 > 6x;                    б). х≥5;      в). х<2,5;

       4x – 6x > 20;                      (-∞;5).         (-∞;2,5).

          – 2x > 20;                 х> -10; (x<-10).                                        

5). Знайти переріз проміжків

1)   х <11   і    х≥3                       

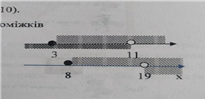[3;11)                                         

2)   x≥8      і     х> 19    

(19;+∞)                                              

 ІV. Вивчення нового матеріалу

Нехай нам потрібно розв'язати наступну задачу.

Дві господарки вирішили сходити в супермаркет та купити помідорів . Одна господарка купила 10 кг помідорів і заплатила за них  більше 9 грн. Друга господарка купила такі ж помідори і заплатила за 5 кг менше 7 грн. Знайти

можливу ціну по якій господарки купували помідори. ( розповідь супроводжується слайдами)

Аналіз задачі призводить до розв'язання системи нерівностей: {10x>9; {x^>0₇^,9; {x>0,9;  {10x>9;

                                    5x<7;                 x^<₅ ^,    x<1,4.           5x<7;

Значить можлива ціна 1кг помідорів від 0,9 грн.  до 1,4 грн.

Отже, ви бачите, що на практиці часто постає питання про відшукання всіх спільних розв'язків нерівностей з однією змінною, тоді говорять, що потрібно розв'язати систему нерівностей.

   Спробуємо сформулювати  алгоритм розв'язання систем лінійних нерівностей.

1.    Розв'язуємо кожну нерівність системи.

2.    Позначаємо множину розв'язків кожної нерівності на одній координатній прямій.

3.    Знаходимо переріз числових проміжків і записуємо відповідь.

             

 V. Фізкультхвилинка

Підведіться. У повітрі правою рукою напишіть своє ім'я. У повітрі лівою рукою напишіть назву улюбленої зірки. Потягніться обома руками до цієї зірки.  Пальчиками рук зобразіть хаос. А  тепер сядьте і продовжимо роботу.

VІ. Закріплення вивченого матеріалу

1)   Чи є числа : -4 і 5  розв'язками системи

3x≤0,

                 {x+7>0; 

2)   Робота з підручником. Розв'язування вправ.

   № 174(усно).

3)   Письмово. Колективне розв'язування № 189(1) – учень біля дошки:

          8(2−x)−2x>3,                     16−8x−2x>3,

        {       −3(6x−1)−x<2x;     −18x+3−x<2x;

 {−−188xx−₋2xx₋>23−x_←163,;         {−₋1021xx>_←−313; ,

3

x<1

¹⁰ ,       x Є ( ;1 ).

₁

x> .

7

Відповідь.  (; 1).

Учень, завантажуючи портал "Школяр України", випадково натрапив на систему, яка містить три нерівності.

Як її розв'язати?

Потрібно розглянути  таку систему:             

2x−6<8,

           4−4 x<10,               {⁻4x<210x−<8¿+66x,>3+9;4,    

6x−9>3;

                                      2x<14,              x<7,

                 −4 x<6 ,     {x>−1,5,  xє(2;7).

                                      6x>12;              x>2.

Відповідь. (2;7).         

Отже, система з трьома нерівностями  розв'язується за тим самим алгоритмом, що й система з двома нерівностями, а у відповіді записується проміжок, який є перерізом розв'язків трьох даних нерівностей.

Рефлексія – розуміння матеріалу, що вивчається.    

 Тоді вчитель пропонує учням подивитися, на скільки їх самооцінка співпаде з результатами  виконання тестових завдань. Учні виконують тестові завдання на комп’ютері у системі MyTestX.

Тести

,

1.    

а) (-∞;1,3);  б) розв'язку немає;  в) (1;+∞);  г) (1;1,3).

y≤4,

                2.{y≥7.

а) розв'язку немає;  б) [4;7];  в) (-∞;4];[7;+∞); г) (4; 7).

3.                                          

.

        a) (-∞;-4);  б) (-4; 2,5); в) (2,5;+∞); г) [-4;2,5].

x<4,

4.x>2, x<3,6.

  а) (2;3,6);  б) (2;4);  в) розв'язку немає;  г) (3,6;+∞).

Підсумок уроку  

1)  Яку мету ставили на початку уроку?

2)  Чи досягли мети протягом уроку?  3) Що нового дізналися ?

Домашнє завдання. Вивчити §6, розв'язати №175, №182(4,5). Скласти або знайти в Інтернеті задачу, розв'язання якої зводиться до системи нерівностей.

Картка самооцінювання   учня 9 класу

№	завдання	Кількість балів
1. 2. 3. 4. 5. 6.	Домашнє завдання Знайти помилку Мікрофон Встановити відповідність Розв'язування вправ Тести Всього	1-2 бали    1бал   1-2 бали   1бал   1-3 бали   2бали

                    Історична довідка

       "Походження знаків нерівності"

Поняття «більше» і «менше» поряд з поняттям «дорівнює» виникли в зв'язку з рахунком предметів і необхідністю порівнювати різні величини. Поняттям нерівності користувались уже древні греки. Наприклад, Архімед (ІІІ ст.  до н. ери), займаючись обчисленням довжини кола, вказав границі числа π.

Ряд нерівностей наводить в своєму відомому трактаті «Основи» Евклід. Він, наприклад, доводить, що середнє геометричне двох додатних чисел не більше їх середнього арифметичного і не менше їх середнього  гармонічного.

Але всі ці роздуми проводились словесно, спираючись в більшості випадків на геометричні терміни.

Сучасні знаки нерівностей з'явились тільки в XVІІ-

XVІІІ столітті.              

Знаки  > і <  увів англійський математик Томас Гарріот (1560-1621) роки  життя. Він був першим алгебраїстом XVІІ століття, являвся вихованцем Оксфордовського університету, склав цінний опис карти місяця, за яким він спостерігав через зорову трубу одночасно з Галілеєм. Новими корисними знаками Гарріота є знаки > і < для відношень «більше» і «менше».  Він їх використовував при розгляді питання про наявність у кубічного рівняння додатних коренів.

Висновок відповідних умов, запропонованих Гарріотом, заслужив потім високу оцінку Жоржа Лагранжа.

 Знаки ≥ і ≤ ввів математик П'єр Бугер (1698-1758).

Це французький вчений, один із засновників фотометрії, написав «Трактат про корабель, про його конструкцію і його рух». Саме цікаве, що Бугер розумів в цілому недостатню теоретичну підготовку кораблебудівників того часу, тому його книга написана простою мовою і не загромаджена математичними викладками, що зробило її на довгі роки підручником для кораблебудівників.