АБСОЛЮТНЕ ПІДСУМОВУВАННЯ РЯДІВ МАТРИЧНИМИ МЕТОДАМИ

УДК 517.52       Камінська Ю. В.

Абсолютне підсумовування рядів матричними методами

у  статті розглядаються основні методи підсумовування збіжних та розбіжних рядів матричними методами, задачі про підсумовування розбіжних рядів  та їх розв’язання різноманітними способами.

Ключові слова: розбіжні ряди, підсумовуюча функція, збіжні ряди, теорема Таубера, методи Чезаро, підсумовування за Пуассоном – Абелем.

The article deals with the basic methods of summing adjacent and divergent series by matrix methods, the problem of summing divergent series and solving them in various ways.

Keywords: divergent series, summation function, convergent series, Tauber theorem, Cesaro methods, Poisson - Abel summation.

Ряди широко використовуються в математиці, особливо при дослідженні різноманітних технічних проблем, пов’язаних з наближеним інтегруванням диференціальних рівнянь, обчисленням значень функцій та інтегралів, розв’язуванням трансцендентних та алгебраїчних рівнянь.

Вони відіграють важливу роль у математиці принаймні з двох причин: є ефективним інструментом математичних досліджень і одним із найважливіших засобів побудови практичних чисельних методів.

Багато математиків минулого працювали над проблемою знаходження суми ряду. Ейлер в статті «Про розбіжні ряди» (1754-1755р.) називає ряд збіжним, якщо його члени прямують до нуля, і розбіжним в іншому випадку. Надаючи кожному ряду числове значення, яке Ейлер називає сумою ряду, він підкреслює, що частинні суми не завжди мають точне значення, рівне сумі.

Отже, підсумувати ряд вдалось в тому випадку, коли ряд збіжний: задача підсумовування зводилась лише до відшукання границі послідовності частинних сум. Що ж стосується розбіжних рядів, то в даному випадку застосування частинних сум не дає бажаного результату. Тому для підсумовування розбіжних рядів необхідно було побудувати іншу теорію.

Поставимо ряду U  у відповідність деяке число S(U) , яке будемо називати його сумою. Ми можемо вважати, що маємо справу з функцією S, визначеною для деяких рядів і яка приймає числові значення. Функцію будемо називати  підсумовуючою функцією. Прикладом такої підсумовуючої функції може бути границя       .

Ця підсумовуюча функція визначена на множині всіх збіжних рядів, і для кожного збіжного ряду її значення рівне звичайній сумі цього ряду. Так визначену конкретну підсумовуючу функцію позначимо через .  

Мета статті: полягає в детальному вивченні основних методів підсумовування збіжних та розбіжних рядів.

Числовим рядом називають вираз  + або

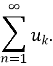
Числа  називаються його членами, а загальним членом ряду.

Утворимо скінчені суми:  ці суми називаються частинними сумами числового ряду.

Якщо існує скінченна границя    послідовності частинних сум, то ряд називається збіжним, а число S вважають його сумою і записують:

Якщо ж границя нескінченна, або зовсім не існує, то ряд називають розбіжним і вважають, що він суми не має.

Найпростішим прикладом нескінченого ряду є геометрична прогресія 

Її частинна сума буде . Якщо , то має скінченну границю: ,  ряд збігається і S буде його сумою.

Ряд називається підсумованим до числа u нижньою трикутною матрицею.

 перетворення ряда в ряд (методом А), якщо виконуються умови:

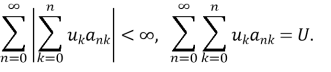
Ряд називається підсумовуваним методом Пуассона-Абеля (А – підсумовуваним до числа ), якщо степеневий ряд збігається при і В результаті різного роду перетворень, зокрема, в результаті переходів від одних рядів до інших, можемо отримати ряди сумовні за Пуассоном-Абелем. У багатьох випадках може викликати інтерес з’ясування збіжності цих рядів у звичайному розумінні.

Таким чином, виникає питання про ознаки збіжності спеціально для тих рядів які є сумовними за Пуассоном-Абелем. Ці ознаки, які відносяться до рядів, що підсумовуються за Пуассоном-Абелем, так і до рядів, що підсумовуються будь-яким іншим методом, зазвичай називаються тауберовими теоремами. Історично перша з них, належить самому Тауберу, полягає в наступному

Теорема (Таубера). Для того, щоб сумовний за Пуассоном – Абелем ряд  що має суму S, збігався в звичайному розумінні ( і мав суму S ) необхідно і достатньо щоб виконувалось граничне відношення

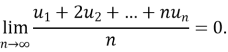
Для методів Чезаро найбільш типовою формою тауберової умови  (що допускає різні узагальнення) є .

Утворимо чезарівські суми порядку ряду. Покладемо 

Біноміальні коефіцієнти – числа Чезаро мають вигляд які є коефіцієнтами біноміального ряду

Чезарівські середні , визначаються співвідношенням

Підсумовування за Чезаро «слабше» ніж підсумовування за Пуассоном – Абелем. Зокрема має місце така теорема.

Теорема. Якщо ряд U підсумовується за Чезаро, то він підсумовується і за Пуассоном-Абелем, і

Обернена теорема не завжди справедлива: існують ряди, які підсумовуються за Пуассоном-Абелем, але не підсумовуються за Чезаро.

Так ряд підсумовується за Пуассоном-Абелем, але не підсумовується за Чезаро.

Із попередньої теореми випливає, що якщо ряд підсумовується за Чезаро то він підсумовується і за Пуассоном-Абелем.

З розглянутого вище  випливає, що для розв’язання задачі про підсумовування розбіжних рядів можна використовувати різноманітні способи. При цьому необхідно обґрунтувати їх лінійність та регулярність. Інколи два методи дають одному і тому ж розбіжному ряду різні узагальнені суми.

ЛІТЕРАТУРА:

1.     Барон С.А. Введение в теорию суммируемости рядов. Таллин: Валгус, 1977. – 275 с.
2.     Давыдов Н.А. Критерии суммируемости расходящейся последовательности к крайней точке её ядра регулярной положительной матрицей // Укр.матем.журн. – 1984. –т.36. - №3.– С.292-297.
3.     Давидов М.О.Тауберові теореми для методів сумування інегралів Лебега // Звітно-наукова конференція кафедр інституту [Київський педагогічний]: тези доповідей (фізико-математичні).– К. – 1965. – С 3-4.
4.     Натансон Й.II. Теория функций вещественной переменной. М.: Просвещение, 1957. – С. 225.
5.     Постников А.Г. Тауберова теория и ее применение. Том 144. – М.: Наука, 1979. – 148с.
6.     Харди Г.Х. Расходящиеся ряды. – М.: Наука. 1951. – 105 с.

Рекомендує  до друку науковий керівник к. ф.-м. н.,  доцент

В. І. Кузьмич