"Тригонометрія в завданнях ЗНО"

ТРИГОНОМЕТРІЯ                                                                                                        В  ЗАВДАННЯХ  ЗОВНІШНЬОГО  НЕЗАЛЕЖНОГО  ОЦІНЮВАННЯ 
Навчальний посібник для підготовки до ЗНО   

     Останні роки важливою та вирішальною подією для випускників загально-освітніх начальних закладів України, а їх же абітурієнтів, є здача тестів зовнішнього незалежного  оцінювання з математики. Тим більше, для випускників загальноосвітніх навчальних закладів України  з 2021 року ДПА з математики буде проводитись у формі ЗНО двох рівнів  обов’язково , і це є  випробуванням для випускників, які бажають оволодіти  вищою освітою з технічних спеціальностей і не тільки. До того ж це одна з оцінок у атестат про середню освіту, яка може суттєво вплинути як на середній бал атестату, так і на отримання вище названого атестату з відзнакою.
        Підсумки ЗНО- 2019 з математики засвідчило, що 15%  абітурієнтів не вміють розкривати дужки; 60% - не знають означення косинуса гострого кута прямокутного трикутника; 67% - не знають визначення логарифма; 35% - не можуть визначити величину кута рівнобедреного трикутника; 75% - не знають основних тригонометричних тотожностей.  Тест з математики     ЗНО-2019 не подолали  поріг «склав/не склав»  понад 18%.
   Тому темою своєї роботи обрав «Тригонометрія в завданнях ЗНО».  Об’єктом свого дослідження обрав завдання ЗНО за попередні роки, а предметом - тригонометрію.   Чому тригонометрія :
   По-перше : тригонометрія вивчається фрагментарно при вивченні геометрії у 8-му і 9-му класах, а більш ретельно в10-му класі, що забувається до закінчення  11-го класу ;
   По-друге  матеріал дуже великий за змістом і різноманітний за видами діяльності . Тут і графіки тригонометричних функцій та їх властивості, велика кількість формул,  обернені тригонометричні функції, тригономет -ричні рівняння, нерівності та їх системи.
   Ось це все і спонукало мене звернути увагу на раніше вивчену тему.  Самостійно опрацювати теоретичний матеріал, систематизувати  знання, відновити уміння та навички, ознайомитися з рівнем завдань ЗНО, створити                                                                                                                                        
деякий методичний посібник, який  може використовуватись  не тільки при підготовці до ЗНО, а і як  матеріал  для  дистанційної  освіти – усе це є метою  роботи .

                                                      РОЗДІЛ І.                                                                                                                                  
                                           1.   Основні  поняття  тригонометрії
    1.1.  Радіанна міра кута .
   У тригонометрії кут розглядається, як фігура утворена при повороті променя на площині навколо початкової точки.

АОВ  утворений  при повороті  променя  ОА  навколо точки  О.

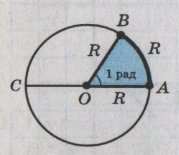Рис. 1.1
   При вимірюванні кутів повороту домовилися, що напрям повороту проти годинникової стрілки вважається додатним, а за годинниковою стрілкою – відємним.
    Таким чином, значення кута повороту ( у градусах ) може набувати всіх дійсних значень від  до  .
1 радіан – центральний кут, що відповідає дузі, довжина якої дорівнює радіусу кола.

          АОС = = ( радіан )

      радіан ;                1 радіан =.

Рис. 1.2.

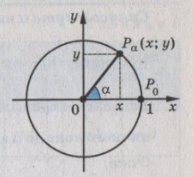1.2. Означення тригонометричних функцій  
            
     Коло радіуса 1 з центром у початку координат називають одиничним колом.
      Введемо означення тригонометричних функцій через одиничне коло.
     Нехай при повороті на кут  точка  переходить у точку . 

Рис. 1.3.                                            
       Синусом кута називається ордината точки одиночного кола :                 sin = y.
     Косинусом кута називається абсциса точки одиночного  кола :   = x.
    Тангенсом кута  називається відношення ординати точки  оди-
ничного кола до її абсциси,  тобто  tg = =  ( де ).                   
    Котангенсом кута  називається відношення абсциси точки  оди-
ничного кола до її ординати,  тобто  ctg = =  ( де ).

  1.3.  Лінії тангенсів і котангенсів
А – лінія тангенсів                 (А) ;                                                           

  СВ – лінія котанге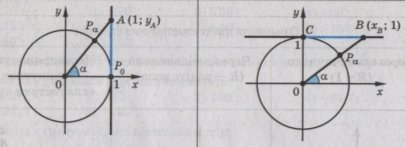нсів                                                         
(СВ
 

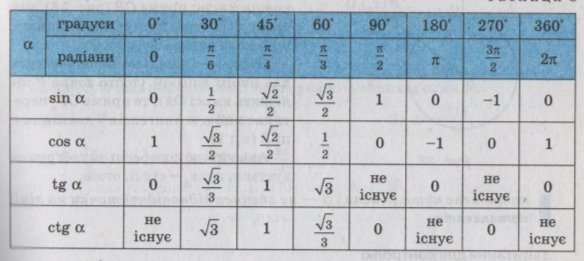
Рис. 1.4.
tg =  - ордината відповідної            ctg =   - абсциса відповідної   
точки лінії тангенсів                                  точки лінії котангенсів 

   1.4.  Значення тригонометричних функцій деяких кутів
                                                                                               Таблиця  1.1.

 

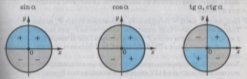     1.5.   Властивості тригонометричних функцій
      1.5.1.  Знаки тригонометричних функцій
       Знаки тригонометричних функцій   легко визначити, виходячи з означення цих тригонометричних функцій   ( див. Рис.1.5.)
Рис. 1.5.

                                                                                                                                          1.5.2   Парність і непарність тригонометричних функцій                                     
    Парність і непарність тригонометричних функцій можна визначити з означень парної і непарної функції  та означень тригонометричних функцій :
          sin ( - = - sin ;     tg ( - = - tg ;    ctg ( - = - ctg   ;
                                         cos ( - = cos .
   Отже, функції синуса, тангенса і котангенса є непарними, а функція косинуса – парна.
     1.5.3.  Періодичність тригонометричних функцій
   Функції  sin x  і  cos x мають найменший додатний період  Т = . Маємо
     sin (   x +  n ) =  sin x  ;    cos (   x +  n ) =  cos x , де  n .
   Причому, для функцій вигляду  y = sin ( kx + b )  і    y = cos ( kx + b )
найменший додатний період визначається за формулою  . 
Функції  tg x  і  ctg x мають найменший додатний період  Т = . Маємо
     tg (   x +  n ) =  tg x  ;    ctg (   x +  n ) =  ctg x , де  n .
   Причому, для функцій вигляду  y = tg ( kx + b )  і    y = ctg ( kx + b )
найменший додатний період визначається за формулою  . 

1.6.   Графіки тригонометричних функцій та їх властивості

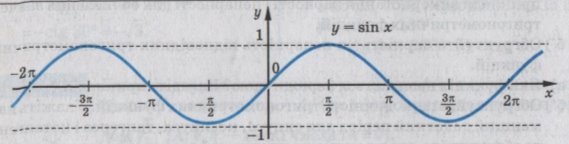
    1.6.1.  Графік функції   y = sin x  та її  властивості 
              Графік функції   y = sin x  ( синусоїда )
  Рис. 1.6.

                      Властивості  функції  у = :
1. Область визначення :  D () = R ;
2. Область значень :  Е () = [ - 1 ; 1 ] ;
3. Функція непарна :   ( графік симетричний відносно початку координат);
4. Функція періодична з періодом  : ;
5. Точки перетину з осями координат :  Оу ( 0 ; 0 ) ;  Ох ( .

6. Проміжки  знакосталості :                                                                                                        
   sin x > 0  при  х ( 2 ;
   sin x < 0  при  х ( 2 ;
7. Проміжки зростання і спадання :
             функція  sin x , якщо  х ( 2 ;
             функція  sin x , якщо  х ( 2 ;
8. Найбільше і найменше значення функції  :
            max ( sin x ) = 1  при  х =   ;
            min ( sin x ) = - 1  при  х = .

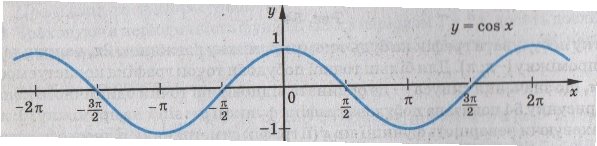
1.6.2.   Графік функції  у = та її властивості

                   Графік функції  у = ( косинусоїда )
Рис. 1.7.

                      Властивості  функції  у = :
1. Область визначення :  D () = R ;
2. Область значень :  Е () = [ - 1 ; 1 ] ;
3. Функція парна :   ( графік симетричний відносно осі Оу );
4. Функція періодична з періодом  : ;
5. Точки перетину з осями координат :  Оу ( 0 ; 1 ) ;  Ох ( .
6. Проміжки  знакосталості :
   соs x > 0  при  х ( + 2 ;
   соs x < 0  при  х ( 2 ;
7. Проміжки зростання і спадання :
             функція  соs x , якщо  х ( 2 ;
             функція  соs x , якщо  х ( 2 ;
8. Найбільше і найменше значення функції  :
max ( cos x ) = 1  при  х =   ;min ( cos x ) = - 1  при  х = . 

                                                                                                                                                                       
     1.6.3.  Графік функції  у =

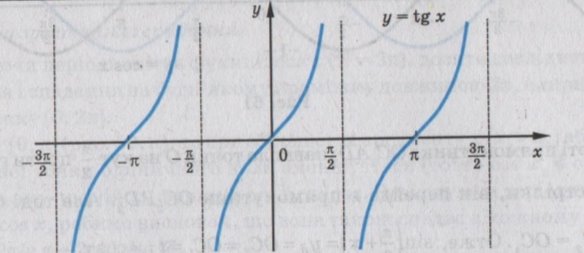
                   Графік функції  у = ( тангенсоїда )
Рис. 1.8.

                      Властивості  функції  у = :
1. Область визначення :  D () :  x ;
2. Область значень :  Е () = R ;
3. Функція непарна :   ( графік симетричний відносно початку координат );
4. Функція періодична з періодом  : ;
5. Точки перетину з осями координат :  Оу ( 0 ; 0 ) ;  Ох ( .
6. Проміжки  знакосталості :
   tg x > 0  при  х ( ;
   tg x < 0  при  х (- ;
7. Проміжки зростання і спадання :
             функція  tg x , якщо  х ( ;           
8. Найбільшого і найменшого значення функція не має .                                                                                                                               

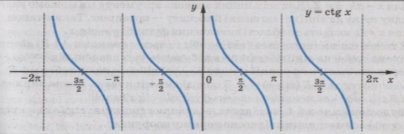1.6.4.  Графік функції  у = та її властивості

Графік функції  у =                  ( котангенсоїда )

1.9.

                                                                                                                                 Властивості  функції  у = :                                                                   
1. Область визначення :  D () :  x ;
2. Область значень :  Е () = R ;
3. Функція непарна :   ( графік симетричний відносно початку координат );
4. Функція періодична з періодом  : ;
5. Точки перетину з осями координат :  Оу (немає ) ;  Ох ( .
6. Проміжки  знакосталості :
   ctg x > 0  при  х ( ;
  ctg x < 0  при  х ( ;
7. Проміжки зростання і спадання :
             функція  ctg x , якщо  х ( ;           
8. Найбільшого і найменшого значення функція не має .

1.7.  Основні тригонометричні формули

     1.7.1.  Співвідношення між тригонометричними функціями одного аргументу

                                   
                                    ( 1.1.)

                                                             tg                                          ( 1.2.)

                                                            ctg                                         ( 1.3.)

                                                      tg                                           ( 1.4.)

                                                      1 +                                        ( 1.5.)
                                                                                               
                                                      1 +                                       ( 1.6.)

   1.7.2.  Формули додавання
                              Косинус  різниці  та  суми :

                   cos (                                       (1.7.)
                   cos (                                      ( 1.8.)
                                        Cинус  суми  та  різниці :                                            

                                     sin (                 ( 1. 9.)
                                     sin (                ( 1. 10.)

                                      Тангенс  суми  та  різниці :
                                             
                                                                                   (1.11.)

                                                                                   (1.12) 

1.7.3.  Формули  подвійного  кута

                                        sin                                             (1.13.)
                   cos2          (1.14.)
                                             tg 2                                                    (1.15.)

 1.7.4.  Формули  пониження степеня
                                                                                                (1.16)
                                                                                                                                  (1.17)     

1.7.5.  Формули  половинного аргументу
                                                                                                       (1.18)
                                                                                                               (1.19)
                                                                              (1.20)                                                 

   1.7.6.  Формули зведення
     Тригонометричні функції від аргументів типу  k
можна зводити до тригонометричних функцій від аргументу  ( де  - гострий  кут ) за таким правилом :
1) знак одержаного виразу визначається знаком початкового виразу, якщо умовно вважати  гострим ;
2) якщо до числа додається число  k, k , то назва функції не змінюється,
якщо додається (2k + 1) , то назва функції змінюється на відповідну кофунк-
цію  ( синус на косинус, косинус на синус, тангенс на котангенс і котангенс
на тангенс ).                                                                                                                                                 
    Корисно користуватись цим правилом за такою послідовністю :
                         чверть знак функція .

1.7.7.  Формули суми і різниці однойменних тригонометричних функцій
                                   sin