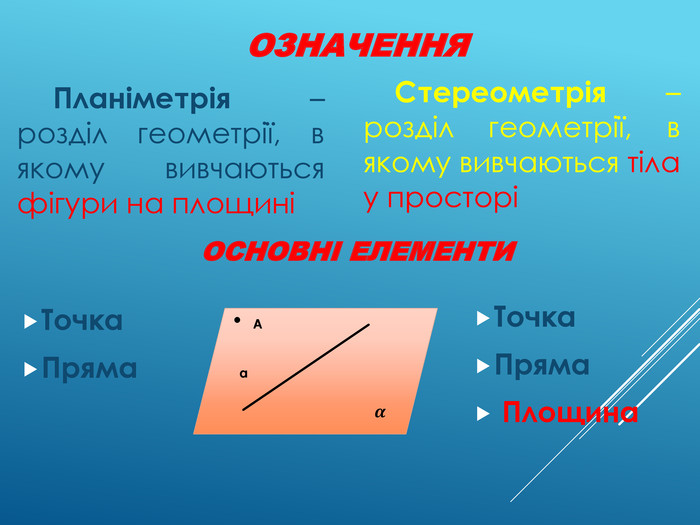
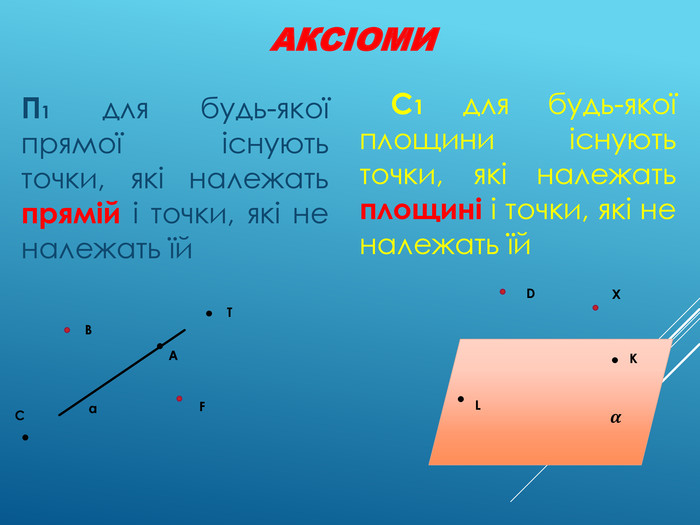
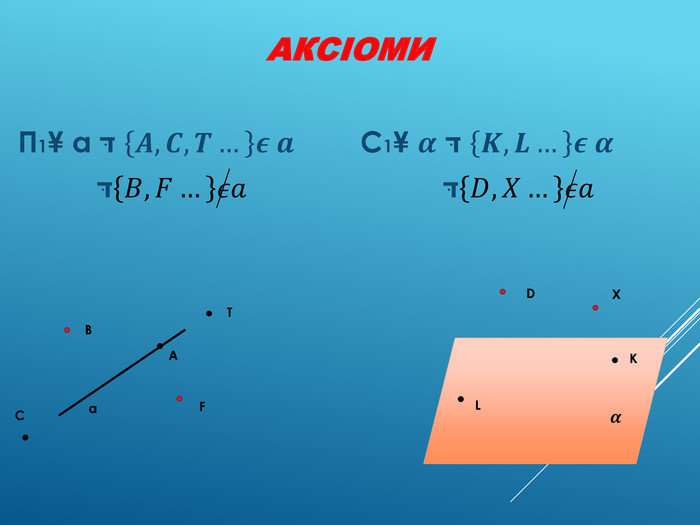
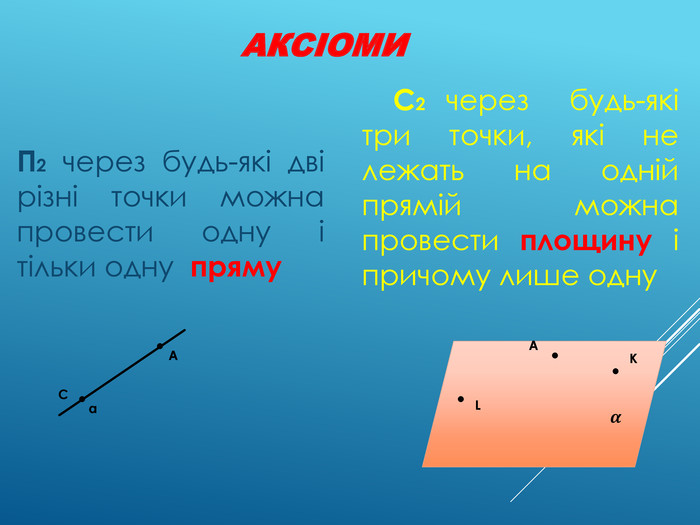
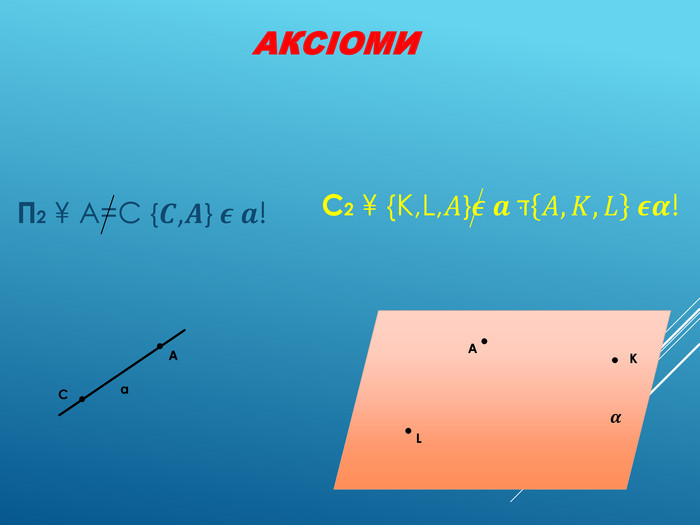
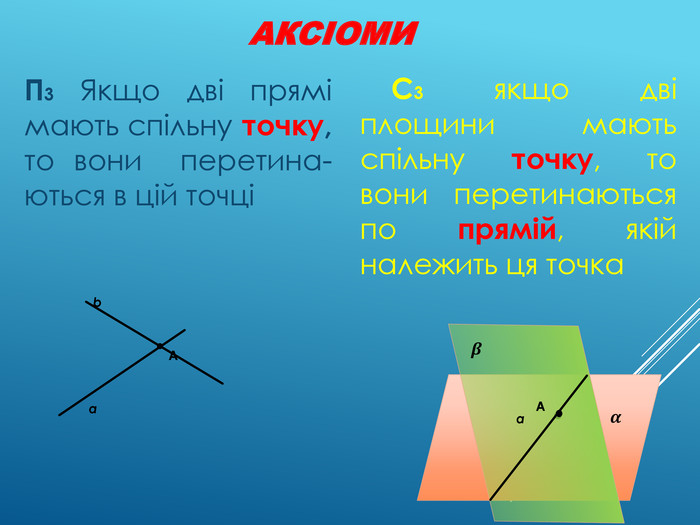
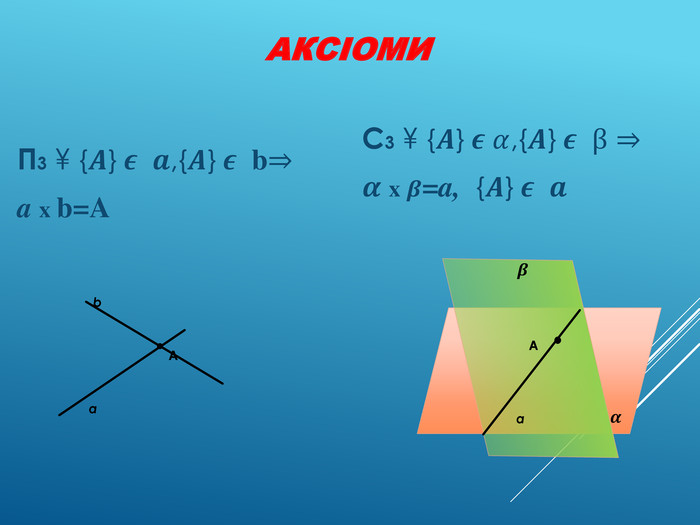
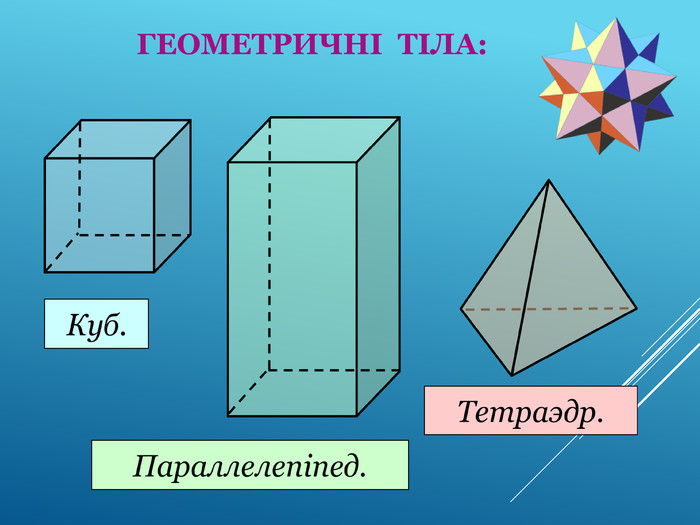
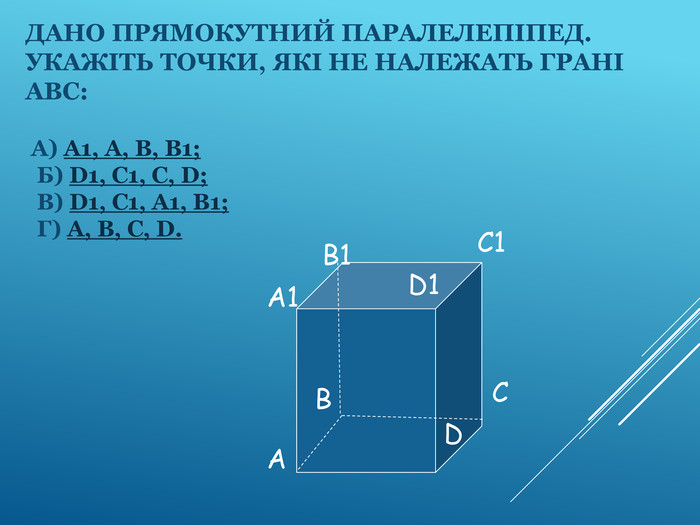
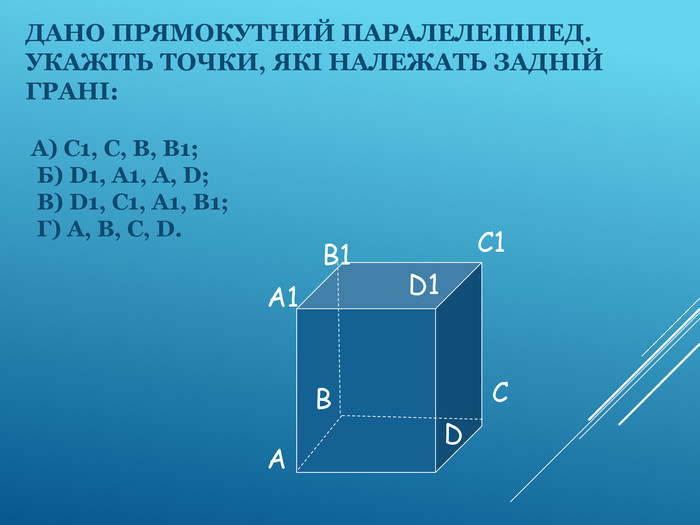
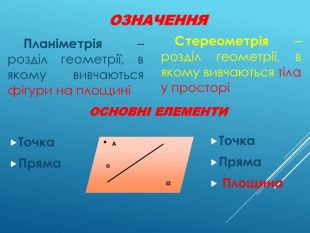
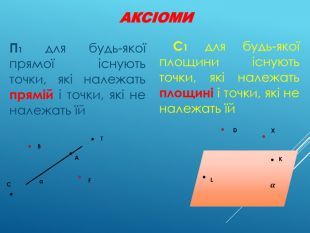
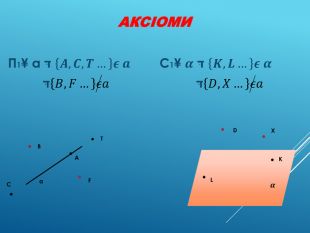
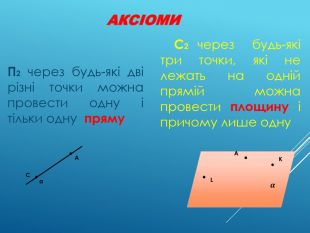
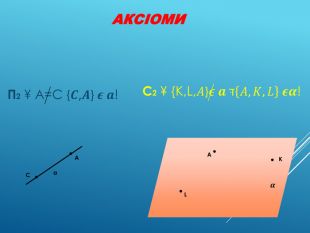
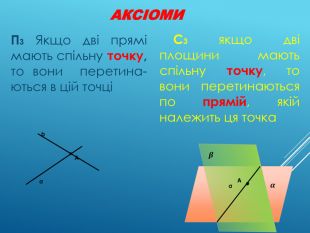
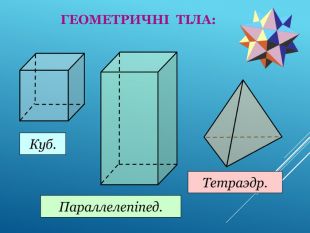
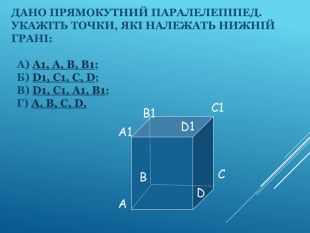
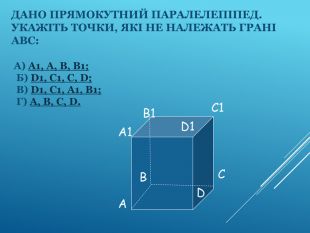
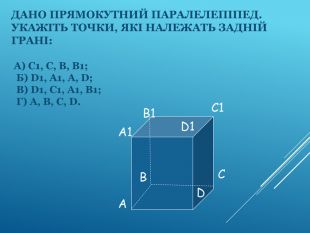
Аксіоми стереометрії (порівняльний аналіз з планіметрією) презентація до уроку
Про матеріал
Це додаток до уроку Аксіоми стереометрії (порівняльний аналіз з планіметрією). До уроку додається ще один матеріал для учня. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку