Алгебра 9 клас

Методичні рекомендації до уроку

Тема уроку: Лінійні нерівності з однією змінною

Мета уроку: домогтися закріплення учнями змісту: означення рівносильних нерівностей та властивостей рівносильних нерівностей; означення лінійної нерівності з однією змінною та схеми її розв’язування залежно від різних  значень коефіцієнтів. Доповнити знання учнів уявленням про схему дій при розв’язування нерівностей з однією змінною, що містять дроби із числовими знаменниками. Продовжити роботу з вироблення вмінь: відтворювати зміст вивчених понять і алгоритмів; застосовувати їх для розв’язування вправ, що передбачають розв’язування лінійних нерівностей з однією змінною.

Тип уроку: закріплення знань, відпрацювання вмінь.

Наочність та обладнання: опорний конспект, роздавальний матеріал (картки з розв’язаннями вправ домашнього завдання).

Хід уроку

1. Організаційний етап

Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

2. Перевірка домашнього завдання

Оскільки вправи домашнього завдання є вправами репродуктивного ( в основному) характеру, то їх перевірку можна здійснити частково (тільки в учнів, що потребують додаткової педагогічної уваги) або запропонувати учням перевірити відповіді за зразком (правильні відповіді заздалегідь записані за дошкою або роздані картки з розв’язаннями для самостійного опрацювання).

3. Формулювання мети і завдань уроку.

Мотивація навчальної діяльності учнів

Для усвідомлення учнями необхідності вивчення матеріалу цього уроку можна певним чином створити проблемну ситуацію: запропонувавши спочатку завдання на повторення (розв’язання рівняння з однією змінною відповідного виду – див. домашнє завдання на повторення), потім перенести ситуацію в нові умови – запропонувати для розв’язування нерівність, яка відрізняється від розв’язаного рівняння тільки знаком (замість знака рівності поставити знак нерівності). Таким чином формулюється проблема: чи можливо розв’язати запропоновану нерівність, здійснюючи ті самі кроки, що і при розв’язуванні рівняння (з урахуванням існуючих відмінностей у властивостях рівностей та нерівностей)? Пошук відповіді на це запитання і є основною метою уроку.

4. Актуалізація опорних знань та вмінь учнів

Усні вправи

1. Чи є правильною нерівність:

1) -8:2<10:(-3);

2) - 5< -1

3) 1-0,8:0,04>-10;

4)

5) (0,12-)·3

2.  Які з чисел : 3; 3,14; 3,1403; π-  є розв’язком нерівності x≤3,14?

3. Розв’яжіть  нерівність:

1) 1 - x<     2) -6x>3;    3) x +2>0 .

4. 3апишіть числові проміжки, що відповідають рисунку:

1)

                -2                                   2           х

2)

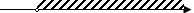
             -2                                    x

3)  

                                              -2              х

4)

                            -2                    2                  х

V. Доповнення знань

Методичний коментар

При роботі над складанням схеми дій для розв’язування нерівностей з однією змінною, які містять дробові коефіцієнти, учні мають усвідомити, що попри існуючу відмінність у властивостях числових рівностей і числових нерівностей схеми дій при розв’язуванні рівнянь і нерівностей першого степеня з однією змінною дуже схожі. Додатково до питання про спосіб розв’язування нерівностей з однією змінною, що містять дробові коефіцієнти, бажано розглянути свого роду протилежний випадок – коли для спрощення процесу розв’язування нерівності доцільно попередньо виконати ділення правої та лівої частин нерівності на НСК коефіцієнтів правої та лівої частин нерівності (для усвідомлення способу відповідних дій можна також запропонувати учням відповідне рівняння з однією змінною).У будь-якому разі після виконання записів розв’язання прикладів учитель має або сам, або залучивши до цього учнів зробити висновок про те, що як і при розв’язуванні рівнянь, так і при розв’язуванні нерівностей перше рівносильне перетворення, яке бажано виконати, - це множення або ділення обох частин на те саме число з метою спрощення виду даної нерівності.

Опорний конспект

6. Формування вмінь

1. Усні вправи

1. 2x<8;                2) 3x≥6;            3)  0x>11;

4. 0x<-7;         5) 0x<8;          6) 0x>-3;

7)  >1; 8)  ><

2. Спостіть вираз:   1) 7(1-2х)+5 х; 2) ; 3) ;  4) х(х+2)-3х(х-1).

Письмові вправи

Для реалізації дидактичної мети уроку слід розв’язати вправи такого змісту:

1. Розв’язати нерівності з однією з змінною, що містять дробові коефіцієнти або цілі коефіцієнти, які мають спільний дільник;
2. Розв’язати нерівності з однією змінною, що потребують застосування тотожних перетворень раціональних виразів;
3. На повторення: завдання на знаходження перерізу та об’єднання числових проміжків, а також на повторення змісту понять системи та сукупності нерівностей з однією змінною.

Методичний коментар

Метою вправ, запропонованих для розв’язування на уроці, є закріплення термінології, вивченої на попередньому уроці, подальше вдосконалення навичок рівносильних перетворень нерівностей з однією змінною, розв’язування лінійних нерівностей з однією змінною, а також вироблення вмінь виконувати дії за схемою, складеною на попередньому етапі уроку.

7. Підсумки уроку

Контрольне завдання. Гра «Хто швидше»

знайде та виправить помилки:

;

;

;

.

Відповідь: (6;+∞ )

8. Домашнє завдання

1. Повторити зміст понять, вивчених на попередньому уроці, а також вивчити схему дій, складену на даному уроці.
2. Розв’язати вправи, аналогічні за змістом вправам класної роботи.
3.  На повторення: знаходження перерізу та об’єднання числових проміжків.